Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d

Подождите немного. Документ загружается.

Существует множество модельных форм псевдопотенциала, в частности, явно

включающие d-резонанс. Однако они, как правило, не обеспечивают достаточно удо-

влетворительное описание ПМ. Недавно модельный псевдопотенциал успешно при-

менялся, чтобы объяснить свойства иридия [65]. Причины хороших совпадений с

экспериментальным данными для этого специфического d-металла не совсем ясны.

2.2 Методы присоединенных плоских волн (ППВ) и

Корринги-Кона-Ростокера (KKR)

Идея других современных методов вычисления зонной структуры состоит в том,

чтобы описать электронные состояния в различных пространственных областях, ис-

пользуя надлежащем образом различные базисы. Обычно вокруг каждой атомной

ячейки строят сферу с объемом, который несколько меньше чем объем кристалли-

ческой ячейки, так чтобы сферы с центрами в различных узлах не пересекались.

Кристаллический потенциал нак аждом узле берется в виде “muﬃn-tin"(MT, потен-

циал типа формочки для выпекания сдобы)

(r) =

v(r) , r < r

, r > r

(2.28)

Внутри сферы потенциал предполагается сферически-симметричным, и соответству-

ющая волновая функция для данной энергии может быть разложена по сферическим

гармоникам

φ(r) =

(r, E)Y

(

r), r < r

(2.29)

- решения соответствующего радиального уравнения Шредингера), что значи-

тельно упрощает вычисления благодаря использованию теории углового момента.

Так как вне сфер потенциал МТ постоянен, базисные волновые функции φ(r)

здесь могут быть выбраны в виде плоских волн. При использовании разложения

(C.28) мы можем сшить решения по непрерывности на границах сфер и определить

коэффициенты C

= C

(

= i

(2l + 1)

(kr

)

, E)

∗

(

k) (2.30)

Функции (2.29) называются присоединенными плоскими волнами (ППВ). Волновые

функции кристалла ищутся в виде линейных комбинаций ППВ с фиксированной

энергией:

(r) =

k−g

(r) (2.31)

Подставляя (2.31) в уравнение Шредингера, легко получить систему линейных

уравнений. Корни соответствующего определителя дают закон дисперсии E(k), ко-

торый сложным образом зависит от кристаллического потенциала. Чтобы получить

результаты с хорошей точностью, достаточно ограничиться не очень большим ко-

личеством членов в (2.31). Практически, используется до 100 ППВ, а для большего

набора решение как правило стабилизируется.

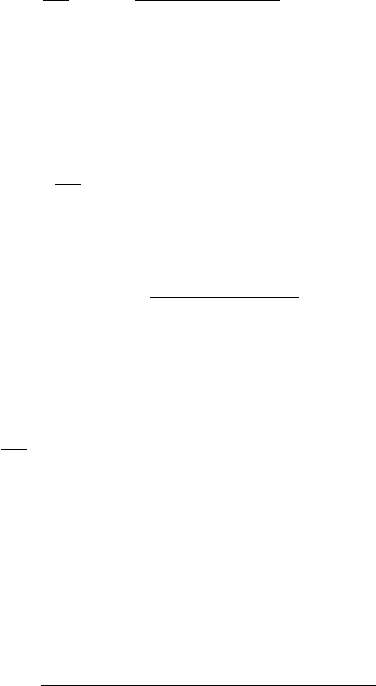
Применение метода ППВ к d-зонам требует расчета с большим числом ППВ

функций по сравнению с s,p-зонами. Однако такие вычисления были выполнены

для всех переходных d-металлов [53,54]. Для 4d- и 5d-металлов становятся важными

релятивистские эффекты (в частности спин-орбитальное взаимодействие). Соответ-

ствующая версия ППВ метода (РППВ метод) была развита Луксом [66].

Метод Функции Грина, развитый Коррингой, Коном и Ростокером (KKR), ис-

пользует внутри МТ сфер, как и ППВ метод, разложение по сферическим гармони-

кам (2.28). В то же время, волновые функции вне сфер представляются не в виде

плоских волн, а также в виде сферических волн, которые рассеиваются от других

узлов. Формально это достигается использованием интегральной формы уравнения

Шредингера (κ = |E|

1/2

)

ψ(r) = −

4π

exp(iκ|r − r

|r − r

V (r

)ψ(r

) (2.32)

Используя условие Блоха

(r + R) = ψ

(r)e

ikR

можно упростить (2.32)

(r) = −

4π

(r − r

, E)v(r

)ψ

) (2.33)

где интегрирование идет по одной ячейке решетки и

(r, E) =

exp(iκ|r − R|)

|r − R|

ikR

(2.34)

- решеточная функция Грина.

Оператор, описывающий систему и соответствующий (2.33), имеет форму

Λ =

dr|ψ

(r)|

4π

Z Z

drdr

∗

(r)v(r)G

(r − r

, E)v(r

)ψ

) (2.35)

Подстановка (2.29) в (2.35) дает [52]

Λ =

lm,l

+ κδ

cot η

(2.36)

Здесь η

- зависящий от l фазовый сдвиг, обусловленный MT потенциалом,

cot η

κr

(κr

) − D

(E)n

(κr

)

κr

(κr

) − D

(E)j

(κr

)

(2.37)

где j

и n

- сферические функции Бесселя и Неймана,

(E) = r

, E)/R

, E) (2.38)

- логарифмические производные радиальной волновой функции. Энергетический

спектр определяется корнями детерминанта матрицы Λ. Структурные константы

A определяются так

lm,l

= 4πκ

R6=0

ikR

(κR) − ij

(κR)]Y

∗

(

lm,l

(2.39)

(величины

C определены в (C. 9)). Эти константы не зависят от кристаллического

потенциала и могут быть рассчитаны один раз для данной решетки.

Преимущество KKR метода по сравнению с ППВ состоит в разделении струк-

турных и атомных коэффициентов. Для одних и тех же решеточных потенциалов

KKR и ППВ методы дают обычно близкие результаты. Детальное соотношение этих

методов обсуждается в [52].

Главная трудность KKR метода - энергетическая зависимость структурных кон-

стант. Однако эта зависимость может быть исключена при использовании так на-

зываемого приближения атомной сферы (ASA), где объем сферы в потенциале МТ

(2.28) выбран равным объему кристаллической ячейки, r

= s, так что объем об-

ласти между сферами исчезает. Для простоты можно положить кинетическую энер-

гию вне атомных сфер E −v

равной нулю, и тогда уравнения ASA-KKR принимают

очень простую форму [56]

det |S

lm,l

(k) − P

(E)δ

| = 0 (2.40)

где потенциальная функция имеет вид

(E) = 2(2l + 1)

(E) + l + 1

(E) − l

(2.41)

и структурные константы не зависят от энергии,

lm,l

(k) = (4π)

1/2

(−1)

(−i)

(2l

+ 1)(2l + 1)

(2λ + 1)

(λ + µ)!(λ − µ)!

+ m

)!(l

− m

)!(l + m)!(l − m)!

R6=0

ikR

∗

λµ

(

R)(s/R)

λ+1

(2.42)

где

λ = l + l

, µ = m − m

Волновые функции, соответствующие MT потенциалу с нулевой кинетической энер-

гией E − v

, могут быть выбраны в форме

(r,E) = i

(

r)φ

(r,E) (2.43)

(r,E) = R

(r, E) ×

(

1 , r < s

+l+1

2l+1

l−D

2l+1

−l−1

, r > s

где коэффициенты определены из условия сшивания по непрерывности и дифферен-

цируемости хвостов на границе MT-сферы. Удобно вычесть член, который описывает

расходящиеся сферические волны. Тогда мы получаем так называемые MT-орбитали

(r,E) = φ

(r,E) ×

(

(r,E)

(s,E)

−

+l+1

2l+1

, r < s

l−D

2l+1

−l−1

, r > s

(2.44)

Условие компенсации хвостов МТ-орбиталей, которые происходят от других узлов,

ведет снова к KKR уравнениям.

Модификация ЛКАО метода, который использует вместо атомных функций

MT-орбитали, называется ЛКMTO методом, причем линейные комбинации MT-

орбиталей конструируются так же, как в (2.1). Подставляя эти функции в уравнение

Шредингера мы получаем ЛКMTO уравнения [67].

В методах ППВ, KKR и ЛКMTO матричные элементы - функции энергии. По-

этому при вычислении собственных значений нужно вычислять определители в каж-

дом точке k-пространства для большого числа значений E (порядка 100) что требует

много времени. Чтобы упростить процедуру вычисления, Андерсен [67] предложил

разложить радиальные волновые функции при некотором значении E, ограничив-

шись линейными членами. Тогда гамильтониан и матрицы перекрытия не зависит от

энергии. Ошибка вследствие линеаризации как правило не превышает погрешности

в потенциале кристалла (в частности вследствие МТ-приближения). Точность может

быть увеличена при учете уровней с более высокими энергиями в разложении. Ли-

нейные методы (ЛMTO и ЛППВ) позволили выполнить расчеты зонной структуры

большого количества переходных металлических составов со сложной кристалличе-

ской структурой [57].

Использование базиса MT-орбиталей позволяют рассчитывать зонную структу-

ру не используя MT-приближения для самого потенциала. Такой подход (ЛMTO-

метод с полным потенциалом) дает возможность значительно улучшить точность

вычислений. Очень хорошие результаты достигнуты также в рамках ЛППВ метода

с использования полного потенциала [68].

2.3 Методы Хартри-Фока-Слэтера и функционала

плотности в проблеме электронных корреляций

Рассмотрение электронного спектра в предыдущих разделах было выполнено в рам-

ках одноэлектронного приближения. Основная задача обсужденных методов вычис-

ления состояла в сшивке атомноподобных решений вблизи узлов решетки с волновы-

ми функциями в окружающем пространстве, где потенциал кристалла V (r) сильно

отличается от атомного. Кулоновское отталкивание между электронами проводи-

мости предполагалось включенным в V (r). Такое включение должно выполняться

самосогласованным способом. В самом простом приближении это может быть до-

стигнуто введением в уравнение Шредингера усредненного кулоновского потенциа-

ла,

(r) = [−

¯h

∆ + V (r) + V

(r)]ψ

(r) (2.45)

(r) = −e

ρ(r

)

|r − r

, ρ(r) = −e

|ψ

(r)|

(2.46)

где суммирование идет по занятым электронным состояниям, а интегрирование

включает суммирование по спиновым координатам.

Уравнения Хартри (2.45) не включают обменного взаимодействия, которое воз-

никает из-за антисимметрии электронных волновых функций. Подставляя антисим-

метризованное произведение одногоэлектронных волновых функций (определитель

Слэтера) (A.2) в уравнение Шредингера для многоэлектронной системы с гамиль-

тонианом (C.1) и минимизируя среднюю энергию

E = hΨ|H|Ψi/hΨ|Ψi

мы получаем уравнения Хартри-Фока

(r) = [−

¯h

∆ + V (r) + V

(r)]ψ

(r)

−e

(r)

∗

)ψ

)

|r − r

(2.47)

где ε

- лагранжевы множители. Обменный член (последний член в левой стороне

(2.47)) имеет нелокальную форму, то есть не сводится к умножению волновой функ-

ции ψ

на потенциальную функцию. Нужно отметить, что члены, описывающие са-

модействие электрона (i = j), сокращаются в кулоновском и обменном вкладах в

(2.47). Из-за ортогональности спиновых функций обменное взаимодействие возни-

кает только между электронами с параллельными спинами.

Параметры уравнения Хартри-Фока зависят, вообще говоря, не только от одно-

электронных квантовых чисел, но и от полных наборов многоэлектронных кванто-

вых чисел в данном состоянии. Например, в многоэлектронном атоме коэффициенты

в параметрах Слэтера (за искличением F

) в разложении на мультиполи кулонов-

ского взаимодействия (C.19) явно зависят от многоэлектронных SL-состояний. Это

приводит к зависимости радиальных волновых функций от квантовых чисел S, L.

Соответствующее выражение для параметров ε

может быть получено так же, как

в [20].

= E(l

SL) −

)

E(l

n−1

) (2.48)

где

E - энергия “замороженного"иона с теми же радиальными функциями, что и у

n-электронного атома, G - генеалогические коэффициенты . Очевидно,

E превыша-

ет энергию истинного иона, которая рассчитывается из уравнения Хартри-Фока. В

системах с большим количеством электронов N разностью E −

E можно пренебре-

гать, так как она дает ошибку только порядка 1/N [9]. Величина (2.48) отличается

от энергии, измеряемой в спектральных экспериментах

(SL, S

) = E(l

SL) −

E(l

n−1

) (2.49)

которая соответствует конкретному переходу SL → S

(эксперименты с не слиш-

ком высоким разрешением дают лоренцевское уширение, которое отличается от

(2.48)).

В зонной теории зависимостью от МЭ квантовых чисел обычно пренебрегают.

Поэтому параметры ε

имеют смысл одноэлектронных энергий, причем −ε

равны

энергии ионизации соответствующего состояния в кристалле (теорема Купменса [9)].

Очевидно, теорема Купменса не выполняется для частично заполненных оболо-

чек переходных металлов, где энергия уровня существенно зависит от заполнения

других состояний (см. Разд.1.1). Метод самосогласованного поля, который рассмат-

ривает только одноэлектронные уровни, не принимают во внимание такие эффекты

корреляций. Однако, простые усредненные обменно-корреляционные потенциалы,

выраженные через электронную плотность, широко используются для вычисления

электронной структуры частично заполненных d-зон в переходных металлах. При

применении к свободным атомам этот подход дает атомные уровни с частичным

заполнениием. Хотя эта картина и не является вполне физически правильной, она

дает удовлетворительное описание атомных и молекулярных спектров [69]. Чтобы

вычислить энергию оптических переходов, нужно найти самосогласованный потен-

циал, рассчитанный в так называемом переходном состоянии, которое соответствует

заполнению уровня на 1/2.

Решение уравнения Шредингера с нелокальным потенциалом, который возни-

кает из-за обменного взаимодействия - очень сложная проблема. Случай свободных

электронов можно рассмотреть аналитически. При выполнении интегрирования для

плоских волн из (2.46) мы получаем

(r) = [

¯h

+ V

(k)]ψ

(r) (2.50)

с локальным обменным потенциалом

(k) = −8

8π

1/3

F (k/k

) (2.51)

где ρ = N/V - электронная плотность,

F (z) =

1 − z

1 + z

1 − z

(2.52)

Логарифмическая особенность в F (z), и, следовательно, в электронном спектре

приводит к нефизическому поведению плотности состояний около уровня Ферми,

N(E → E

) → 0. Эта особенность появляется из-за дальнодействующего харак-

тера кулоновского взаимодействия и должна на самом деле устраняться эффекта-

ми корреляции, которые приводят к экранированию. Таким образом приближение

Хартри-Фока оказывается недостаточным для описания газа свободных электронов

из-за сильной k-зависимости. Чтобы избежать этой трудности, Слэтер [69] предло-

жил использовать потенциал, который описывает движение электрона в усреднен-

ном обменном поле.

Обменный потенциал для данного состояния может быть представлен в форме

(r) = −e

∗

(r)ψ

∗

)ψ

(r)ψ

)

|r − r

/[ψ

∗

(r)ψ

(r)] (2.53)

Выражение (2.53) может интерпретироваться как потенциал заряда с величиной e,

который удален из дырки, окружающей i-ый электрон. Мы можем записать для

усредненного потенциала

(r) = −e

∗

(r)ψ

∗

)ψ

(r)ψ

)

|r − r

∗

(r)ψ

(r) (2.54)

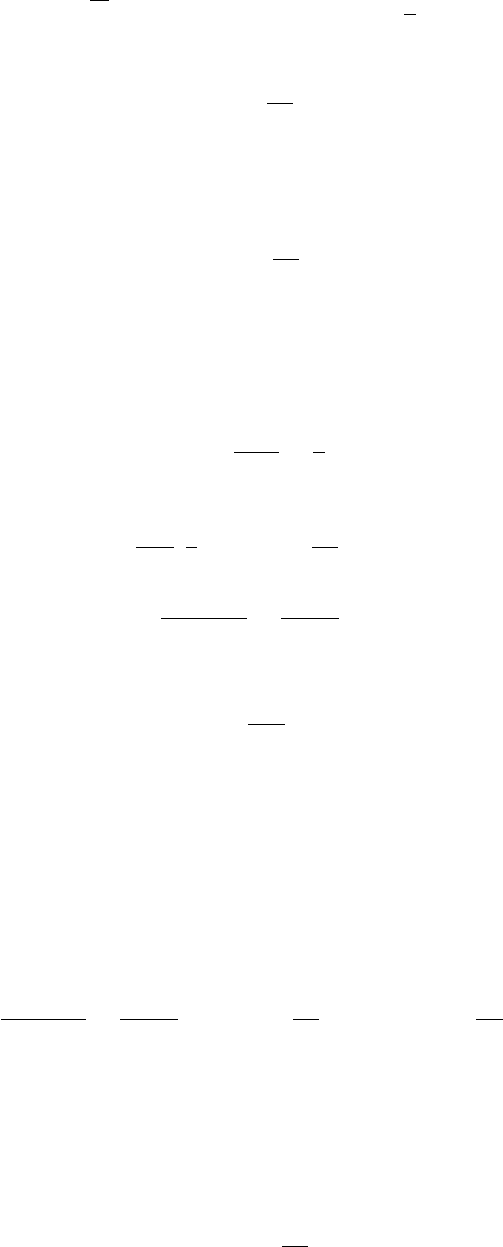
Усредняя потенциал газа свободных электронов (2.51) по k мы получаем

F =

dzF (z)/

dz =

(2.55)

= −6

8π

1/3

(2.56)

Стартуя с выражения (2.56), Слэтер ввел локальный обменно-корреляционный по-

тенциал с такой же зависимостью от электронной плотности

(r) = −6

8π

ρ(r)

1/3

(2.57)

В другом подходе к проблеме построения обменно-корреляционного потенциала [70]

используется явное вычисление полной энергии. Интегрируя одноэлектронную энер-

гию для электронного газа, можно получить

E = 2

k<k

[

¯h

(k)]

[

)

−

2π

]

2.21

)

−

0.916

Ry (2.58)

где Ry = e

/2a

=13.6 эВ,

4πρ

1/3

(2.59)

является радиусом сферы с объемом, который соответствует одному электрону для

данной однородной плотности ρ. В единицах боровского радиуса a

величина r

име-

ет порядок отношения потенциальной энергии электрона к средней кинетической

энергии. Для реалистических металлических значений r

= 2 ÷ 6 второе слагаемое

в (2.58), которое происходит от обменного взаимодействия, становится сравнимым с

первым. В пределе высокой плотности проблема электронного газа может рассмат-

риваться более строго путем разложения E по r

[12]:

E =

2.21

)

−

0.916

+ 0.622 ln

− 0.096 + O

¶¸

Ry (2.60)

Поправки в (2.60) описывают эффекты корреляции за пределами приближения

Хартри-Фока.

Учитывая обменную энергию однородного газа, приходящуюся на частицу, и пре-

небрегая корреляциями, мы получаем обменный потенциал Гаспара-Кона-Шэма[70]

GKS

(r) = −4

8π

ρ(r)

1/3

(2.61)

Этот потенциал отличается от приближения (2.57) множителем 2/3. Так получается

потому, что операции варьирования полной энергии и статистического усреднения не

коммутируют. Выражение (2.60) может быть также получено из потенциала (2.51)

подстановкой k = k

(F = 1/2).

Более общее выражение для обменно-корреляционного потенциала (xα-

потенциал) может быть записано так

xα

(r) = V

(r) (2.62)

Оптимизация параметра α < 1 позволяет учесть эффекты электронных корреля-

ций. Потенциал (2.61) был успешно применен для расчета электронной структуры

большого числа твердых тел [69,57]. Однако причины этого успеха не были понятны,

пока не был развит метод функционала плотности. Результаты xα-вычислений для

чистых металлов оказались не слишком чувствительными к выбору α. Более ранние

вычисления с α = 1 дали результаты, которые удовлетворительно согласовывались

с экспериментальными данными и были близки к данным для оптимального α. По-

видимому, это связано с тем, что ошибка в полной энергии для α = 1 частично ком-

пенсируются увеличением глубины потенциальной ямы. Однако правильный выбор

α, важен для металлических и изоляторных соединений. Для переходных метал-

лов атомные плотности обычно берутся для конфигурации d

n−1

s в 3d- и 4d-рядах

и для конфигурации d

n−2

в 5d-рядах, причем оптимальные значения α лежат в

интервале 0.65÷0.8.

Важный шаг в теории электронных корреляций в твердых телах был сделан

Хоэнберг и Кон [59], которые доказали общую теорему, согласно которой энергия

основного состояния является однозначным функционалом электронной плотности.

Кон и Шэм [70] ввели этот функционал плотности (DF) в форме

E[ρ(r)] =

drρ(r)V

ext

(r) +

Z Z

drdr

ρ(r)ρ(r

)

|r − r

+T [ρ(r)] + E

[ρ(r)] (2.63),

где V

ext

- внешний потенциал ионов решетки, T - кинетическая энергия невзаи-

модействующих электронов с плотностью ρ, функционал E

соответствует вкла-

ду обмена и корреляций. Подход DF может быть обобщен для рассмотрения спин-

поляризованных систем.

Представляя электронную плотность в форме (2.46) и варьируя (2.63) относи-

тельно ψ

, мы получаем

(r) = [−

¯h

∆ + V

ext

(r) + V

(r)]ψ

(r) (2.64)

где лагранжевы множители ε

соответствуют энергиям квазичастиц, обменно-

корреляционный потенциал V

определяется варьированием E

по отношению к

плотности,

(r) = δE

[ρ(r)]/δρ(r) (2.65)

Таким образом, многоэлектронная проблема сводится к одночастичной с локаль-

ным обменно-корреляционным потенциалом корреляции. Однако нужно отметить,

что подход DF гарантирует только значение энергии основного состояния, описывает

точно распределение заряда и спиновой плотности и связанные с ними физические

величины. К ним принадлежат упругие характеристики и обменные параметры, ко-

торые выражаются через соответствующие энергетические разности, магнитный мо-

мент насыщения и т.д. С другой стороны, квазичастицы Кона не совпадают с истин-

ными электронами, так что волновые функции ψ

не имеют прямого физического

смысла. Поэтому возможность вычисления полного спектра возбуждения, вообще

говоря, не оправдана. Особенно сомнительно описание состояний, далеких от E

, и

поведение при конечных температурах. Однако метод DF широко используется для

рассмотрения различных физических свойств.

Истинный функционал (2.63), разумеется, неизвестен, и приходится использо-

вать некоторые приближения. Формально точное выражение для E

может быть

представлено в виде кулоновского взаимодействия электрона с дыркой при учете

обменной корреляции, которая окружает их:

[ρ(r)] =

drρ(r)

(r, r

− r)

|r − r

(2.66)

Соответствующая электронная плотность может быть получена путем интегрирова-

ния по константе связи λ [71,72]

(r, r

− r) = ρ(r

)

dλ[g(r, r

, λ) − 1] (2.67)

где g - парная корреляционная функция. Так как дырка содержит один электрон,

плотность заряда должна удовлетворять правилу сумм

(r, r

− r) = −e (2.68)

Функционал E

фактически зависит от сферически усредненной плотности заряда,

что следует из изотропного характера кулоновского взаимодействия [72]. Действи-

тельно, замена переменной в (2.66) позволяет провести интегрирование по углам

вектора r − r

drρ(r)

(r,R)

(r,R) =

dΩρ

(r,R) (2.69)

Таким образом, приближенное выражение для E

может дать точные результа-

ты, даже если детальное описание ρ

(в частности, ее несферической компоненты)

неточно.

Далее мы должны конкретизировать форму корреляционной функции. В при-

ближении локальной плотности (LDA), которое как правило используется в вычис-

лениях зонной структуры, ρ

берется в той же самой форме, что и для однород-

ной электронной плотности с заменой ρ → ρ (r) и соответствующей корреляционной

функцией g

(r, r

− r) = ρ(r)

dλ[g

(|r − r

|, λ, ρ(r)) − 1] (2.70)

Подставляя (2.70) в (2.69), мы получаем LDA функционал, который имеет локаль-

ную форму

[ρ] =

drρ(r)ε

(ρ) (2.71)

где ε

- обменная и корреляционная энергия на один электрон для взаимодейству-

ющего однородного электронного газа. Эта величина была численно рассчитана с

высокой точностью, причем имеются различные интерполяционные аналитические

формулы. Поэтому подход LDF позволяет конструировать различные локальные по-

тенциалы, учитывающие обмен и корреляцию. Самый простой обменный потенциал

дается xα-выражением (2.61). Это выражение может быть обобщено следующим об-

разом

(r) = β(r

GKS

(r) (2.72)

Таким образом, xα-метод получает обоснование в теории функционала плотности,

причем параметр α зависит от электронной плотности. Значение α изменяется от

2/3 до 0.85, в то время как r

увеличивается от нуля (предел высокой плотно-

сти) до значений, которые являются типичными для металлов в межатомной об-

ласти (r

= 4). Примером интерполяционного приближения является потенциал

Хедина-Лундквиста [73], которому соответствует

(z) = 1 + 0.0316z ln(1 + 24.3/z) (2.73)

Приближение функционала локальной спиновой плотности (LSD), которое приме-

няется для рассмотрения магнитных переходных металлов, выглядит как

[ρ

↑

, ρ

↓

] =

drρ(r)ε

(ρ

↑

(r), ρ

↓

(r)) (2.74)

Простой LSDA потенциал Барта-Хедина [74] в первом порядке по спиновой поляри-

зации m(r) = n

↑

(r) − n

↓

(r) имеет вид

(r) =

σδ(n)

m(r)

n(r)

GKS

(r) (2.75)

где n(r) = n

↑

(r) + n

↓

(r) и параметр δ учитывают эффекты корреляции. В пределе

высокой плотности δ = 1, и δ = 0.55 для r

= 4.

LD приближение переупрощает общий DF подход, который основан на теореме

Хоэнберга-Кона. В частности, LDA не принимает во внимание правильной зависимо-

сти ρ

(r, r

) от ρ(r) в пустом пространстве (ср. (2.67) с (2.70)). Однако этот метод да-

ет хорошие результаты в случае медленно меняющейся плотности ρ(r). Кроме того,

приближение хорошо работает в пределе высокой плотности, так как оно включает

правильную кинетическую энергию системы в отсутствие взаимодействия.

В оригинальных статьях [70] были сделаны попытки принять во внимание неодно-

родные поправки к LDA, разлагая ρ

по ρ(r). Однако такое разложение дает только

малые вклады и не работает в случае сильно неоднородных электронных систем

(например, для 4f-электронов в редкоземельных элементах и узких d-зон), и поэто-

му, строго говоря, неправомерно для ПM. Другие модификации LDA обсуждаются

в обзоре [72]. Проблема учета мультиплетной структуры в подходе функционала

плотности обсуждается в [75,76].

Ирхин В.Ю., Ирхин Ю.П. Электронная структура, корреляционные эффекты и физические свойства d - и f-переходных металлов и их соединений

Подождите немного. Документ загружается.