Информационные технологии в науке, образовании и производстве ИТНОП-2010. Материалы IV-й Международной научно-технической конференции. Том 2

Подождите немного. Документ загружается.

ИТНОП-2010

111

УДК 004.272

А.С. ОЛЕНИН

О СТРУКТУРНОМ ПОДОБИИ ВЫЧИСЛИТЕЛЬНЫХ ЗАДАЧ

Рассматриваются вопросы создания условий, при которых архитектура компьютера на

ранних этапах проектирования могла бы функционировать с учетом специфики больших задач;

отмечено важное значение для этого концепции подобия.

Ключевые слова: архитектура компьютера; граф вычислений; структурное подобие.

Problems of conditions creation at which a computer architecture at early design stages could

function in view of specificity of greater problems are considered, the great value for this purpose the

concept of similarity is noted.

Keywords: computer architecture; calculation graph; structural similarity.

В больших реальных задачах наиболее существенно проявляются разнообразие,

сильная связанность всех структурных элементов между собой и зависимость их

функционирования от динамически формируемых данных. Все эти и многие другие

объективные особенности сложных вычислений должны учитываться при разработке

компьютерных систем, так как в противном случае потенциальные возможности ускорения

счета, заложенные в структуре задач, будут реализованы неэффективно.

В связи со сказанным поставим следующий вопрос. Как создать условия, при которых

проектируемая вычислительная система уже на ранних стадиях разработки (например, в виде

ограниченной имитационной модели) могла бы функционировать с учетом специфики

больших задач? Если этого не сделать, нам практически до завершения проекта недоступны

сколько-нибудь существенные объективные данные о функционировании компьютера на

задачах крупномасштабной информационной и структурной емкости.

Уместно вспомнить, что похожая ситуация имела место еще в докомпьютерную эпоху

в ряде областей науки и техники. Например, при конструировании летательных аппаратов

сначала проводились тщательные исследования на малых моделях в аэродинамических

трубах. В результате экспериментов оценивались многие важные факторы, влияющие на

конструкцию реальных аппаратов. Благодаря таким исследованиям, технические и

экономические качества разработок существенно повышались. Для нашего дальнейшего

рассмотрения важно отметить, что в этих работах основанием для переноса данных,

полученных в условиях маломасштабных моделей, на масштаб реальных объектов, служило

подобие физических процессов при соблюдении известных критериев подобия. Появление

компьютеров позволило существенным образом развернуть эту проблему в сторону

компьютерного моделирования, так как в принципе стало возможным исследовать любую

крупномасштабную задачу (доступную ресурсам компьютера) без привлечения дорогих

натурных экспериментов. При этом точность и достоверность компьютерного

моделирования всецело зависима от качества математических моделей, разрабатываемых

специалистами по научно-прикладным задачам.

Однако в отличие от исследований в областях приложений вычислительных систем

ситуация в области разработки самих вычислительных систем принципиально иная. Это,

прежде всего, связано с тем, что никакая модель проектируемого компьютера не может быть

сравнима по производительности с реально действующей машиной. Поэтому применение

даже наиболее мощных компьютеров для функционирования такой модели не в состоянии

обеспечить ее обкатку на реальных крупномасштабных задачах, для которых, в первую

очередь, и предназначена разработка. Для того чтобы преодолеть этот «замкнутый круг»,

может оказаться полезной упомянутая выше концепция подобия. Необходимо иметь ответ на

следующий вопрос: при каких условиях результаты исследований, полученные на малых

IV Международная научно-техническая конференция

112

масштабах (с помощью модели), можно переносить на масштабы больших задач, которые

предстоит решать будущей реальной машине. Опыт исследований в этом направлении

показывает, что главным объектом, определяющим свойство подобия, в данном случае

является вычислительный граф, описывающий содержание задачи в структурной форме.

Иными словами, если структура (граф) вычислений на малых и больших масштабах

сохраняется примерно постоянной, то, несмотря на возможный разброс, результаты

моделирования в обоих случаях обязательно должны коррелировать между собой, то есть

нести информацию друг о друге.

Таким образом, чтобы эффективно использовать принцип подобия при разработке

вычислительных систем, необходимо: во-первых, уметь выполнять расчеты на малых и

больших масштабах с неизменным графом вычислений и, во-вторых, уметь делать это для

сложных структур, присущих большим задачам. Остановимся подробнее на этих условиях.

Для достижения первого условия автором на основе комплексного анализа

постановок задач разработан экспериментальный набор [1] типовых вычислений,

ориентированный на физико-математические приложения. Особенность набора состоит в

том, что он содержит типовые алгоритмы, характерные для данной сферы приложений. Эти

алгоритмы уже непосредственно в своей структуре отражают такие фундаментальные

свойства больших задач, как линейность и нелинейность, стационарность и

нестационарность, непрерывность и дискретность, детерминированность и случайность,

многомерность и т.д. Каждая программа набора плавно масштабируема, что позволяет

проводить исследования как на малых, так и на больших масштабах вычислений при

неизменном графе.

Переходя ко второму условию, следует отметить, что каждая отдельная большая

задача имеет довольно жесткую структурную организацию, поэтому результаты ее

моделирования часто неприменимы к каким-либо другим, столь же большим задачам.

Однако интересы разработчиков вычислительных систем требуют, чтобы представленные в

их распоряжение тестовые задачи широко отражали характерные свойства реальных

вычислений. В этом случае появляются основания для объективной оценки проекта по

спектру приложений на ранних этапах проектирования.

Изложенные соображения естественным образом подводят нас к проблеме

приближения произвольной вычислительной структуры совокупностью базовых структур.

Математические методы приближенного анализа давно известны и эффективно

используются при решении многих научно-технических задач. Это, например, методы,

связанные с аппроксимациями произвольной функции набором базисных функций,

произвольного вектора набором базисных векторов и т.д. Применение аппарата

приближений играет огромную роль в развитии многих областей научных исследований.

Однако проблема структурных приближений выглядит, на наш взгляд, значительно сложнее

по сравнению с проблемами математических приближений. Здесь встают чрезвычайно

трудные (с точки зрения формальных подходов) проблемы: во-первых, как определять

характерный базис вычислительных структур, а во-вторых, как формировать произвольную

структуру на основе базисного набора.

Автором на первом этапе предложен семантический метод решения указанной

проблемы, опирающийся на смысловой анализ процесса моделирования задач. Удобно

показать суть этого метода на конкретном примере. Возьмем, например, в качестве базиса

набор типовых вычислений, указанный выше, и на его основе построим приближенный

аналог реальной задачи.

Рассмотрим вычислительную структуру решения двумерной задачи Навье-Стокса для

несжимаемой вязкой жидкости. В одной из формулировок эта задача состоит из двух

нестационарных уравнений в частных производных для скоростей течения и уравнения

Пуассона для давления. Мы не будем выписывать здесь эти хорошо известные уравнения, а

обратимся к наиболее существенной (в данном аспекте) вычислительной стороне дела.

Алгоритм решения задачи сводится к поочередному расчету полей скорости и давления в

ИТНОП-2010

113

каждый момент времени с использованием информации об этих полях в предыдущие

моменты. Во многих случаях нестационарные уравнения решаются с помощью какой-либо

явной схемы, а для решения уравнения Пуассона применяется какой-нибудь прямой метод.

Акцентируя внимание именно на структуре вычислений, важно отметить следующее

обстоятельство. В основе разностных схем лежит шаблон сетки, устанавливающий тип связи

данного узла с его ближайшими соседями. Использование такого шаблона в явной форме

определяет структуру вычислений любой явной схемы, различия же в конфигурации

шаблонов, часто существенные в математическом смысле, практически не добавляют ничего

качественно нового в ход вычислительного процесса. Поэтому в структурном смысле (а не в

математическом), приближением множества явных схем может служить любая структурно

подобная явная схема, в которой заложены характерные свойства множества явных схем.

Таким образом, имея в составе базисного набора программы, реализущие двумерную

явную схему и такие прямые методы решения уравнения Пуассона, как быстрое

преобразование Фурье или циклическая редукция, можно осуществить приближенное

моделирование реальной задачи Навье-Стокса в ее структурном подобии. Если

соответствующие программы имеют масштабируемые параметры: размер сетки и число

шагов по времени, то, в соответствии с общей схемой решения, интерпретирующая

программа будет действовать так, как это делается в реальной задаче. Три базисные

программы поочередно работают на заданном размере сетки, выполняя общее для них

заданное число итераций по времени. Несмотря на простоту, описанная приближенная

модель, очевидно, отражает характерные структурные свойства реальной задачи. Для нее не

являются существенными (в структурном смысле) конкретный вид коэффициентов

уравнений, их правых частей и численные значения величин. В широком диапазоне этих

факторов структура вычислений остается качественно неизменной, что позволяет отделить

внутреннее структурное содержание задачи от ее количественных многообразий.

Итак, на примере конкретной постановки задачи Навье-Стокса мы сконструировали

приближенную модель, которая более сложна, чем исходные базисные программы, близка по

структуре к реальной задаче и может работать как на малых, так и на больших масштабах.

Аналогичным образом с помощью базисного набора опробованы структурно

подобные модели других реальных задач. Эти модели, несмотря на приближенный характер,

тем не менее интерпретируют реальную семантику больших задач и, обладая свойствами

подобия, позволяют учитывать структуру крупномасштабных вычислений на ранних

моделях проектируемых систем.

ЛИТЕРАТУРА

1. Оленин А.С. Принципы типизации вычислений. //Системы и средства информатики.

Вып.16. – М.: Наука, 2006. – С. 386–392.

Оленин Анатолий Степанович

Московский физико-технический институт, г. Москва

Д. физ.-мат. н., старший научный сотрудник, доцент

Тел.:8 (499) 126-84-35

E-mail:

aolenin@yandex.ru

IV Международная научно-техническая конференция

114

УДК 519.8:004.056

М.Ю. РЫТОВ, В.И. АВЕРЧЕНКОВ, Т.Р. ГАЙНУЛИН

ФОРМАЛИЗАЦИЯ ВЫБОРА РЕШЕНИЯ

ПРИ ПРОЕКТИРОВАНИИ СИСТЕМ ЗАЩИТЫ ИНФОРМАЦИИ

ОТ НЕСАНКЦИОНИРОВАННОГО ДОСТУПА

В статье рассматриваются вопросы проектирования комплексных систем защиты

информации с использованием специализированных объектно-ориентированных САПР

Ключевые слова: комплексные системы защиты информации; специализированные

объектно-ориентированные САПР; математические модели.

In the article the problems of integrated security systems design automation by means of

creation of a specialized object-oriented CAD are viewed.

Keywords: integrated systems of information protection; specialized object-oriented CAD;

mathematical models.

Широкое использование в процессе информатизации общества современных методов

и средств обработки информации создало не только объективные предпосылки повышения

эффективности всех видов деятельности личности, общества и государства, но и ряд проблем

защиты информации, обеспечивающей требуемое ее качество. Сложность решения этой

проблемы обусловлена необходимостью создания целостной системы комплексной защиты

информации, базирующейся на стройной её организации и регулярном управлении.

Рассматривая концептуальную модель процесса защиты информации [1], становится

очевидным, что защита информации – динамический процесс. Чем совершеннее

современные способы несанкционированного доступа и более реальны источники угроз, тем

более актуальным ставится проблема создания необходимого рубежа защиты информации. В

то же время, чем грамотнее выбраны и реализованы направления и способы защиты, тем

дальше отходят угрозы от защищаемой информации. Рубеж защиты «плавает» во времени в

зависимости от тех или иных выше названных факторов.

Таким образом, проектировать (разрабатывать заново или в большинстве случаев, как

показывает практика, модифицировать существующую) комплексную систему защиты

информации (КСЗИ) следует для конкретного момента времени, объективно оценивая

положение рубежа защиты. В целях обеспечения соответствия КСЗИ современному уровню

обеспечения безопасности и для снижения трудоемкости, обеспечения качества проектных

решений, а главное, сокращения сроков её проектирования целесообразно применять

специализированные системы автоматизированного проектирования (САПР).

В настоящее

время задача автоматизации проектирования КСЗИ сводится к обработке экспертных данных

с выдачей решений общего рекомендательного характера.

Как показывает практика, системы автоматизированного проектирования и принятия

решения в сфере информационной безопасности достаточно новые. Широко известны и

применяются лишь системы, позволяющие автоматизировать аудит информационной

безопасности, такие как «Кондор», «Авангард» или «Гриф».

Комплексная система защиты информации – это система, в которой действуют в

единой совокупности правовые, организационные, технические, программно-аппаратные и

другие нормы, методы, способы и средства, обеспечивающие защиту информации от всех

потенциально возможных и выявленных угроз и каналов утечки. Элементы КСЗИ в свою

очередь, в общем виде, состоят из средств, устройств и способов защиты информации, а

также методов их использования.

Понятие защиты информации в настоящее время ассоциируется, как правило, с

проблемами обеспечения информационной безопасности информационных систем.

ИТНОП-2010

115

Информационные системы способствуют значительному повышению эффективности и

скорости информационных процессов, однако при этом резко возрастают угрозы

несанкционированного доступа к их ресурсам. Эти угрозы могут вызывать значительные

неблагоприятные последствия для государства, общества, бизнеса и отдельных граждан.

Информационные системы, для которых следует проектировать КСЗИ, можно

классифицировать по виду используемой информации на два типа – системы, в которых

циркулирует государственная тайна и конфиденциальная информация. Организация защиты

государственной тайны жестко регламентирована Законом РФ «О государственной тайне» и

другими документами, утвержденными в соответствии с этим законом, защитой секретной

информации занимаются ФСБ, ФСО и ряд других спецслужб; острой необходимости в

разработке специализированных САПР комплексных систем защиты секретной информации

нет. В то же время задача автоматизации проектирования КСЗИ информационных систем от

несанкционированного доступа для обработки информации конфиденциального характера

является актуальной. Методы, подходы и средства, применяемые для разработки КСЗИ

подобных систем, нормативно-правовыми документами четко не определяются, и у

разработчиков есть возможность выбора тех или иных методов и средств защиты

конфиденциальной информации.

На основе анализа накопленного опыта по исследованию и практической разработке

автоматизированных систем проектирования сложных технических машиностроительных

объектов, специализированных объектно-ориентированных САПР, САПР технологических

процессов [2] была предложена концепция построения специализированной САПР КСЗИ от

несанкционированного доступа.

При создании САПР КСЗИ была реализована следующая структурно-

функциональная схема, представленная на рисунке1.

Рисунок 1 – Структурно-функциональная модель САПР КСЗИ

На начальных этапах проектирования происходит получение модели объекта защиты,

в основу которой положено структурирование элементов информационной системы,

определение характеристик процесса проектирования, определяется категория

Моделирование объекта

защиты

Моделирование и

ранжирование угроз

Аудит

информационной

безопасности объекта

защиты

Разработка технического

задания на

проектирование КСЗИ

Проектирование КСЗИ

Проектирование

организационной

структуры

Модуль выбора средств

защиты информации от

НСД

План-проект

КСЗИ объекта

Оптимизация

проекта КСЗИ

достигнута

Внедрение КСЗИ

на объект

Виды обеспечения САПР

КСЗИ

Техническое

Математическое

Информационное

Лингвистическое

Программное

Проектные модули

САПР КСЗИ

Да

Не

IV Международная научно-техническая конференция

116

информационной системы и виды обрабатываемой информации, возможные людские,

материальные и финансовые ограничения КСЗИ, технические характеристики объектов).

Далее выполняется моделирование возможных угроз несанкционированного доступа

к ресурсам информационной системы и их ранжирование

На следующем этапе осуществляется аудит информационной безопасности

информационной системы на основе требований международных стандартов по

информационной безопасности и нормативных документов Российской Федерации [3]. В

ходе проведения аудита проводится анализ используемой в защищаемой системе

информации, определяются её виды, степень конфиденциальности, ценность, актуальность и

важность и выявляются все виды угроз, которым может быть подвергнута защищаемая

информационная система и все возможные каналы утечки информации. Затем на стадии

проектирования комплексной системы защиты информации происходит выбор конкретных

средств защиты и оптимизация предлагаемых проектных решений.

Для построения математической модели выбора средств защиты информации от

несанкционированного доступа была использована модель с полным перекрытием

Клементса - Хофмана [4]. Данная модель позволяет оценить защищенность информационной

системы, рассчитать затраты на построение системы защиты, а так же определить

оптимальный вариант построения системы информационной безопасности.

В предлагаемой модели безопасности с полным перекрытием (модели Клементса-

Хофмана) проводилось описание взаимодействия «области угроз», «защищаемых объектов»

(ресурсов информационной системы) и «системы защиты» (механизмов безопасности

информационной системы).

Для описания комплексной системы защиты информации с полным перекрытием

рассматривались три вида множества:

•

множество угроз U = {u

}, i = m,1 ;

•

множество объектов защиты O = {o

}, j = n,1 ;

•

множество механизмов защиты M = {m

}, k = r,1 .

Элементы множеств U и O находятся между собой в определенных отношениях

«угроза» – «объект», определяемых двухдольным графом G(X,E), где Х – множество вершин

графа X = {x

i+j

}, i = m,1 , j = n,1 , а Е

– множество дуг графа. Дуга <U

, O

> существует

только тогда, когда U

является средством получения доступа к объекту O

Цель защиты состоит в том, чтобы «перекрыть» каждую дугу графа и воздвигнуть

барьер для доступа по этому пути. Общая постановка задачи формулируется в следующем

виде: множество средств защиты информации М обеспечивает защиту множества объектов О

от множества угроз U. В идеале каждое средство m

должно характеризовать некоторое

ребро <U

, O

> из указанного графа. В действительности, эти средства выполняют функцию

«брандмауэра», обеспечивая некоторую степень сопротивления попыткам проникновения.

Это сопротивление – основная характеристика присущая всем элементам множества М.

Применение множества средств защиты М преобразует 2-дольный граф в 3-дольный.

В защищённой системе все рёбра представляются в виде:

, М

> и <М

, O

При этом одно и то же средство защиты может перекрывать более одной угрозы и

защищать более одного объекта.

Развитие этой модели предполагает введение еще двух элементов:

V – набор уязвимых мест, определяемый подмножеством декартова произведения

U×O: v

= <u

, o

>. Таким образом, под уязвимостью системы защиты будет пониматься

возможность осуществления угрозы u

в отношении объекта o

(на практике под уязвимостью

системы защиты обычно понимается не сама возможность осуществления угрозы

безопасности, а те свойства системы, которые способствуют успешному осуществлению

угрозы, либо могут быть использованы злоумышленником для осуществления угрозы);

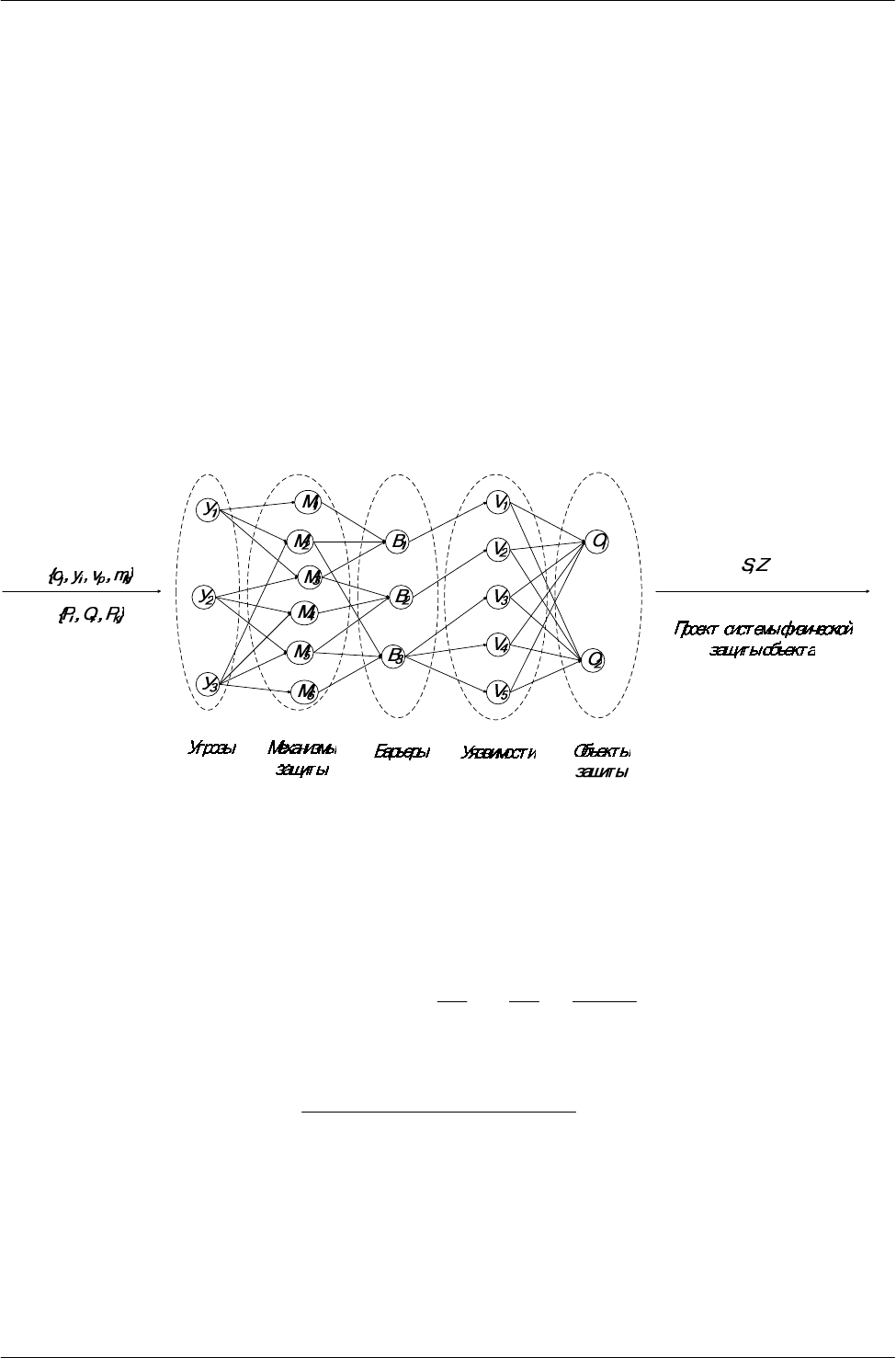
ИТНОП-2010

117

B – набор барьеров, определяемый декартовым произведением V

M: b

= <u

, o

>, представляющих собой пути осуществления угроз безопасности, перекрытые

средствами защиты.

Таким образом, процесс защиты можно представить с помощью 5–мерного кортежа:

S={O, U, M, V, B}, (1)

где: О – множество защищаемых объектов;

U – множество возможных угроз;

М – множество средств защиты;

V – множество уязвимых мест, представляющих собой пути проникновения в

систему;

В – множество барьеров, представляющих собой те точки в которых требуется

осуществить защиту в системе.

Комплексная система защиты с полным перекрытием предусматривает средства

защиты на каждый возможный путь проникновения. В такой системе каждому уязвимому

месту v

соответствует барьер b

.(рис. 2)

Рисунок 2 – Модель комплексной системы защиты информации от несанкционированного доступа

В идеале каждый барьер защиты должен исключать соответствующий путь

реализации угрозы. В действительности же механизмы защиты обеспечивают лишь

некоторую степень сопротивляемости угрозам безопасности. Прочность барьера

характеризуется величиной остаточного риска R

, связанного с возможностью осуществления

угрозы y

в отношении объекта o

при использовании барьера b

Эта величина определятся по формуле:

= P

⋅

(1 – P

), ;,1,,1,,1 nmqnjmi ×=== (2)

Для определения защищенности всей системы была предложена следующая

зависимость:

( )( )

( )

[

)

1,0,1,0,

∈∈

−⋅⋅

∑

∈∀

qji

PQP

(3)

где P

– вероятность появления угрозы y

– величина ущерба при удачном осуществлении угрозы y

в отношении

защищаемого объекта o

– степень сопротивляемости барьера b

, характеризующаяся вероятностью его

преодоления.

IV Международная научно-техническая конференция

118

В зависимости (3) знаменатель определяет суммарную величину остаточных рисков,

связанных с возможностью осуществления угроз безопасности U в отношении объектов

защиты O, при использовании механизмов защиты M. Суммарная величина остаточных

рисков характеризует «общую уязвимость» системы защиты, а защищенность системы

определяется как величина, обратная ее «уязвимости». При отсутствии в системе барьеров

, перекрывающих определенные уязвимости, степень сопротивляемости механизма защиты

принимается равной 0

Построение комплексной системы защиты требует затрат на построение барьера b

Затраты на создание барьеров защиты определяются как C = {c

Таким образом, если реализован барьер защиты b

и при этом происходит угроза

V = {y}

, то суммарный ущерб составит величину:

= Q

+ c

(4)

При создании комплексной системы защиты информации задача оптимизации

формулируется следующим образом – при минимальных затратах достичь максимальной

защищенности ресурсов информационной системы:

•

минимизации суммарных затрат (С → min);

•

максимизации защищенности ресурсов информационной системы (S → max)

Поставленная задача относится к задачам принятия решений в условиях

неопределенности.

Для принятия решения в таких задачах необходимо оценить суммарные затраты

путем составления математической модели в виде матрицы результатов решений или

оценочной матрицы <A, F, Y>. Здесь А – множество альтернатив (возможностей выбора), F –

множество негативных факторов (угроз), оказывающих воздействие информационные

объекты организации, а Y – множество возможных исходов. Под альтернативой

miAa

,1, =∈

понимаются варианты построения барьеров b

- из различных механизмов

защиты m

∈

M, k = r,1 , имеющихся в распоряжении, под факторами f

∈

F, nj ,1= ,

подразумеваются угрозы y

. Результат, ожидаемый при каждом сочетании вариантов

решения и объективных условий, соответствует суммарным затратам

= Q

+ c

С учетом этих условий может быть формирована оценочная матрица (таблица 1).

Таблица1 – Оценочная матрица эффективности и стоимости средств защиты

В приведенной таблице а

– начальное состояние системы без средств защиты.

Для принятия решения необходимо привести все значения к безразмерному виду,

чтобы иметь возможность их оценить. При использовании метода свёртки и нормализации

критериев задача сводится к нахождению экстремума функции (в данном случае –

минимума, поскольку затраты надо минимизировать):

∑

YYextr minZ . (5)

Все

приводятся к безразмерному виду по следующей формуле:

= Q

+ c

= Q

+ c

… … …

+ c

= Q

+ c

… … …

ИТНОП-2010

119

( )

max

, (6)

где max(

) – максимальное значение

в данном столбце.

Для исключения влияния размерности шкал, вводятся нормировочные

коэффициенты p

(один на столбец). Каждый коэффициент p

рассчитывается по формуле:

∑

(7)

затем все s

приводятся к нормальному виду:

= s

⋅

. (8)

В этом случае значения – безразмерны и нормированы, т.е. их можно сравнивать между

собой.

Для получения окончательного результата необходимо сложить значения

получившихся исходов Y (n

= s

⋅

) построчно и выбрать в образовавшемся векторе,

оптимум, соответствующий решению задачи, в данном случае – минимуму.

Если значение суммарных затрат для данной альтернативы a

отвечает заданным

требованиям по минимуму, а показатель защищенности S для этой альтернативы –

требованиям по максимуму (или, по крайней мере, удовлетворяет владельца

информационной системы), то эта альтернатива, т.е. вариант построения барьеров защиты b

является оптимальным.

Данный метод используется, если точно известны затраты на создание комплексной

системы защиты информации и возможный ущерб в денежном выражении. Если ущерб

выражен в относительных единицах, то сначала необходимо провести нормализацию и

свертку значений ущерба Q

и затрат на систему защиты c

, и только потом – суммарных

затрат

Результатом работы САПР КСЗИ является разработка документированного

организационно-технического проекта КСЗИ от несанкционированного доступа,

определяющего комплексное использование правовых, организационных, инженерно-

технических, программно-аппаратных и криптографических методов, средств и способов

защиты информации, обрабатываемой в информационной системе.

В составе САПР КСЗИ разработаны семь видов обеспечения, адаптированных к

рассматриваемой области проектирования с учетом её специфики.

Разработанная методология автоматизации проектирования КСЗИ может быть

использована при проектировании КСЗИ от несанкционированного доступа для

промышленных предприятий, государственных учреждений и коммерческих организаций, а

также при оценке эффективности и модернизации существующих на объектах систем

защиты информации.

ЛИТЕРАТУРА

1. Аверченков В.И., Рытов М.Ю. Организационная защита информации. – Брянск: Изд-во

БГТУ, 2005. – 184 с. – (Серия «Организация и технология защиты информации»).

2. Аверченков В.И. САПР технологических процессов, приспособлений и режущих

инструментов: учеб. пособие для вузов / В.И. Аверченков, И.А. Каштальян, А.П.

Пархутик. – Минск: Вышэйш. шк., 1993. – 288 с.

3. Аверченков В.И. Аудит информационной безопасности. – Брянск: Изд-во БГТУ, 2005. –

184 с. – (Серия «Организация и технология защиты информации»).

IV Международная научно-техническая конференция

120

4. Хоффман, Л. Д. Современные методы защиты информации / Под ред. В.А. Герасименко. –

М.: Сов. радио, 1980. – 264 с.

Аверченков Владимир Иванович

Брянский государственный технический университет, г. Брянск

Заведующий кафедрой «Компьютерные технологии и системы»

Д.т.н., профессор

Тел.: +7(4632)56-49-90

E-mail: aver@tu-bryansk.ru

Рытов Михаил Юрьевич

Брянский государственный технический университет, г. Брянск

Директор центра по информационной безопасности, к.т.н., доцент

Тел.: +7(4632)56-49-90

E-mail: rmy@tu-bryansk.ru

Гайнулин Тимур Ринатович

Брянский государственный технический университет, г. Брянск

К.т.н., доцент кафедры «Компьютерные технологии и системы»

E-mail: rmy@tu-bryansk.ru

Тел.: +7(4632)56-49-90