Hull J.C. Risk management and Financial institutions

Подождите немного. Документ загружается.

160

Chapter 6

See O. Vasicek "Probability of Loss on a Loan Portfolio," Working Paper KMV, 1987.

Vasicek's results were published in Risk in December 2002 under the title "Loan Portfolio

Value".

This is also when equation (6.10) is satisfied. Hence,

To simplify matters, we suppose that the distribution Q

of time to

default is the same for all i and equal to Q. We also assume that the

copula correlation between any two names is the same and equals Since

the copula correlation between companies i and j is this means that

the for all i. Equation (6.11) becomes

For a large portfolio of loans, this equation provides a good estimate of

the proportion of loans in the portfolio that default by time T. We will

refer to this as the default rate.

As F decreases, the default rate increases. How bad can the default rate

become? Because F has a standard normal distribution, the probability

that F will be less than There is therefore a probability of Y

that the default rate will be greater than

Define V(T, X) as the default rate that will not be exceeded with

probability X, so that we are X% certain that the default rate will not

exceed V(T, X). The value of V(T, X) is determined by substituting

Y = 1 — X into the above expression:

This result was first developed by Vasicek in 1987.

Example 6.2

Suppose that a bank has lent a total of $100 million to its retail clients. The

one-year probability of default on every loan is 2% and the amount recovered

in the event of a default averages 60%. The copula correlation parameter is

Correlations and Copulas 161

estimated as 0.1. In this case,

showing that we are 99.9% certain that the default rate will not be worse than

12.8%. Losses when this worst-case loss rate occur are 100 x 0.128 x (1 — 0.6),

or $5.13 million.

SUMMARY

The measure usually considered by a risk manager to describe the relation-

ship between two variables is the Covariance rate. The daily Covariance rate

is the correlation between the daily returns on the variables multiplied by

the product of their daily volatilities. The methods for monitoring a

Covariance rate are similar to those described in Chapter 5 for monitoring

a variance rate. Either EWMA or GARCH models can be used. In

practice, risk managers need to keep track of a variance-covariance matrix

for all the variables to which they are exposed.

The marginal distribution of a variable is the unconditional distribution

of the variable. Very often an analyst is in a situation where he or she has

estimated the marginal distributions of a set of variables and wants to

make an assumption about their correlation structure. If the marginal

distributions of the variables happen to be normal, it is natural to assume

that the variables have a multivariate normal distribution. In other situa-

tions copulas are used. The marginal distributions are transformed on a

percentile-to-percentile basis to normal distributions (or to some other

distribution for which there is a multivariate counterpart). The correlation

structure between the variables of interest is then defined indirectly from an

assumed correlation structure between the transformed variables.

When many variables are involved, analysts often use a factor model.

This is a way of reducing the number of correlation estimates that have to

be made. The correlation between any two variables is assumed to derive

solely from their correlations with the factors. The default correlation

between different companies can be modeled using a factor-based Gaus-

sian copula model of their times to default.

FURTHER READING

Cherubini, U., E. Luciano, and W. Vecchiato, Copula Methods in Finance,

Wiley, 2004.

162

Chapter 6

Demarta, S., and A.J. McNeil, "The t Copula and Related Copulas," Working

Paper, Department of Mathematics, ETH Zentrum, Zurich, Switzerland.

Engle, R. F., and J. Mezrich, "GARCH for Groups," Risk, August 1996, 36-40.

Vasicek, O. "Probability of Loss on a Loan Portfolio," Working Paper, KMV,

1987. [Published in Risk in December 2002 under the title "Loan Portfolio

Value".]

QUESTIONS AND PROBLEMS (Answers at End of Book)

6.1. If you know the correlation between two variables, what extra information

do you need to calculate the Covariance?

6.2. What is the difference between correlation and dependence? Suppose that

y = x

and x is normally distributed with mean 0 and standard deviation 1.

What is the correlation between x and y?

6.3. What is a factor model? Why are factor models useful when defining a

correlation structure between large numbers of variables?

6.4. What is meant by a Positive-semidefinite matrix? What are the implica-

tions of a correlation matrix not being Positive-semidefinite?

6.5. Suppose that the current daily volatilities of asset A and asset B are 1.6%

and 2.5%, respectively. The prices of the assets at close of trading yester-

day were $20 and $40 and the estimate of the coefficient of correlation

between the returns on the two assets made at that time was 0.25. The

parameter used in the EWMA model is 0.95. (a) Calculate the current

estimate of the Covariance between the assets. (b) On the assumption that

the prices of the assets at close of trading today are $20.50 and $40.50,

update the correlation estimate.

6.6. Suppose that the current daily volatilities of asset X and asset Y are 1.0%

and 1.2%, respectively. The prices of the assets at close of trading yester-

day were $30 and $50 and the estimate of the coefficient of correlation

between the returns on the two assets made at this time was 0.50.

Correlations and volatilities are updated using a GARCH(1,1) model.

The estimates of the model's parameters are = 0.04 and = 0.94. For

the correlation, = 0.000001, and, for the volatilities, = 0.000003. If

the prices of the two assets at close of trading today are $31 and $51, how

is the correlation estimate updated?

6.7. Suppose that in Problem 5.15 the correlation between the S&P 500 Index

(measured in dollars) and the FTSE 100 Index (measured in sterling) is

0.7, the correlation between the S&P 500 Index (measured in dollars) and

the USD/GBP exchange rate is 0.3, and the daily volatility of the S&P 500

Index is 1.6%. What is the correlation between the S&P 500 Index

Correlations and Copulas 163

(measured in dollars) and the FTSE 100 Index when it is translated to

dollars? (Hint: For three variables X, Y, and Z, the Covariance between

X + Y and Z equals the Covariance between X and Z plus the Covariance

between Y and Z.)

6.8. Suppose that two variables V

and V

have uniform distributions where all

values between 0 and 1 are equally likely. Use a Gaussian copula to define

the correlation structure between V

and V

with a copula correlation of

0.3. Produce a table similar to Table 6.3 considering values of 0.25, 0.5,

and 0.75 for V

and V

. (A spreadsheet for calculating the cumulative

bivariate normal distribution can be found on the author's website:

www.rotman.utoronto.ca/~hull.)

6.9. Assume that you have independent random samples z

, z

, and z

from a

standard normal distribution and want to convert them to samples e

, e

and e

from a trivariate normal distribution using the Cholesky decom-

position. Derive three formulas expressing e

, e

, and e

in terms of z

, z

and z

and the three correlations that are needed to define the trivariate

normal distribution.

6.10. Explain what is meant by tail dependence. How can you vary tail

dependence by the choice of copula?

6.11. Suppose that the marginal distributions of V

and V

are standard normal

distributions but that a Student t-copula with four degrees of freedom and

a correlation parameter of 0.5 is used to define the correlation between the

variables. How would you construct a chart showing samples from the

joint distribution?

6.12. In Table 6.3 what is the probability density function of V

conditional on

V\ < 0.1. Compare it with the unconditional distribution of V

6.13. What is the median of the distribution of V

when V

equals 0.2 in the

example in Tables 6.1 and 6.2.

6.14. Suppose that a bank has made a large number of loans of a certain type.

The total amount lent is $500 million. The one-year probability of default

on each loan is 1.5% and the loss when a default occurs is 70% of the

amount owed. The bank uses a Gaussian copula for time to default. The

copula correlation parameter is 0.2. Estimate the loss on the portfolio that

is not expected to be exceeded with a probability of 99.5%.

ASSIGNMENT QUESTIONS

6-15. Suppose that the price of gold at close of trading yesterday was $300 and

its volatility was estimated as 1.3% per day. The price of gold at the close

of trading today is $298. Suppose further that the price of silver at the

close of trading yesterday was $8, its volatility was estimated as 1.5% per

164

Chapter 6

day, and its correlation with gold was estimated as 0.8. The price of silver

at the close of trading today is unchanged at $8. Update the volatility of

gold and silver and the correlation between gold and silver using (a) the

EWMA model with =0.94, and (b) the GARCH(1,1) model with

= 0.000002, = 0.04, and = 0.94. In practice, is the parameter

likely to be the same for gold and silver?

6.16. The probability density function for an exponential distribution is

where x is the value of the variable and A. is a parameter. The cumulative

probability distribution is Suppose that two variables V

and V

have exponential distributions with of 1.0 and 2.0, respectively. Use a

Gaussian copula to define the correlation structure between V

and V

with

a copula correlation of —0.2. Produce a table similar to Table 6.3 using

values of 0.25, 0.5, 0.75, 1, 1.25, 1.5 for V

and V

. (A spreadsheet for

calculating the cumulative bivariate normal distribution can be found on

the author's website: www.rotman.utoronto.ca/~hull.

6.17. Create an Excel spreadsheet to produce a chart similar to Figure 6.5

showing samples from a bivariate Student t-distribution with four degrees

of freedom where the correlation is 0.5. Next suppose that the marginal

distributions of V

and V

are Student t with four degrees of freedom but

that a Gaussian copula with a copula correlation parameter of 0.5 is used

to define the correlation between the two variables. Construct a chart

showing samples from the joint distribution. Compare the two charts you

have produced.

6.18. Suppose that a bank has made a large number loans of a certain type. The

one-year probability of default on each loan is 1.2%. The bank uses a

Gaussian copula for time to default. It is interested in estimating a

"99.97% worst case" for the percentage of loans that default on the

portfolio. Show how this varies with the copula correlation.

Bank Regulation

and Basel II

An important objective of governments is to provide a stable economic

environment for private individuals and businesses. One way they do this

is by providing a reliable banking system where bank failures are rare and

depositors are protected. Shortly after the disastrous crash of 1929, the

United States took a number of steps to increase confidence in the

banking system and protect depositors. It created the Federal Deposit

Insurance Corporation (FDIC) to provide safeguards to depositors in the

event of a failure by a bank. It also passed the famous Glass-Steagall Act

that prevented deposit-taking commercial banks from engaging in invest-

ment banking activities.

Deposit insurance continues to exist in the United States and many

other countries today. However, many of the provisions of the Glass-

Steagall Act in the United States have now been repealed. There has been

a trend worldwide toward the development of progressively more compli-

cated rules on the capital that banks are required to keep. This is because,

as shown in Section 1.3, the ability of a bank to absorb unexpected losses

is critically dependent on the amount of equity and other forms of capital

held. In this chapter we review the evolution of the regulation of bank

capital from the 1980s and explain the new Basel II capital requirements,

which are scheduled to be implemented starting in 2007.

It is widely accepted that the capital a financial institution requires

should cover the difference between expected losses over some time horizon

and "worst-case losses" over the same time horizon. The worst-case loss is

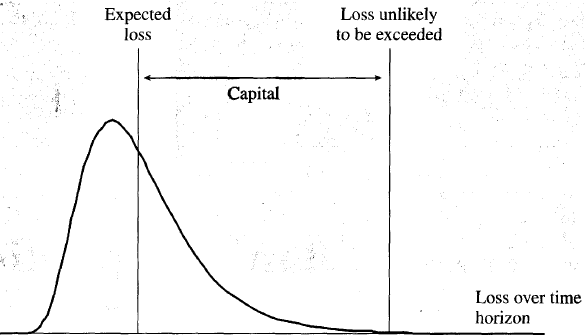
166

Chapter 7

Figure 7.1 The loss probability density function and the capital

required by a financial institution.

the loss that is not expected to be exceeded with some high degree of

confidence. The high degree of confidence might be 99% or 99.9%. The

idea here is that expected losses are usually covered by the way a financial

institution prices its products. For example, the interest charged by a bank

is designed to recover expected loan losses. Capital is a cushion to protect

the bank from an extremely unfavorable outcome. This is illustrated in

Figure 7.1.

Banks compete in some financial markets with securities firms and

insurance companies. These types of financial institutions are often

subject to different regulations from banks. In the United States securities

firms are regulated by the Securities and Exchange Commission (SEC),

and insurance companies are regulated at the state level with national

guidelines being set by the National Association of Insurance Commis-

sioners (NAIC). However, the regulators of all financial institutions face

similar problems. Bank regulators want to protect depositors and ensure

a stable financial system; insurance regulators want to protect policy-

holders from defaults by insurance companies and ensure that the public

has confidence in the insurance industry; securities regulators want to

protect the clients of brokers from defaults and ensure that markets

operate smoothly. In some instances the three types of regulators find

themselves specifying capital for the same financial instruments. If they

do not do this in the same way, there is liable to be what is known as

regulatory arbitrage, with risks being shifted to those financial institutions

that are required to carry least capital for the financial instruments.

Bank Regulation and Basel II 167

There have been some signs of convergence in the regulation of

financial institutions. Insurance regulators and securities regulators are

adopting similar approaches to bank regulators in prescribing minimum

levels for capital. In the European Union the Capital Requirements

Directive (CRD) legislation will require the regulatory capital for secur-

ities firms to be calculated in a similar way to that for banks. Another

initiative by the European Union, Solvency II, is likely to lead to the

capital for insurance companies in Europe being calculated in a broadly

similar way to that for banks.

Bank regulators are in many ways taking the lead in developing a

methodology for setting capital requirements for financial institutions.

The regulation of banks is based on international standards, whereas the

regulation of other types of financial institutions varies more from

country to country. For this reason the regulation of banks will be the

main focus of this chapter.

7.1 REASONS FOR REGULATING BANK CAPITAL

It is tempting to argue as follows: "Bank regulation is unnecessary. Even

if there were no regulations, banks would manage their risks prudently

and would strive to keep a level of capital that is commensurate with the

risks they are taking." Unfortunately, history does not altogether support

this view. There is little doubt that regulation has played an important

role in increasing bank capital, making banks more aware of the risks

they are taking.

If markets operated totally without government intervention, banks

that took risks by keeping low levels of equity capital would find it

difficult to attract deposits and might experience a "run on deposits",

where large numbers of depositors try to withdraw funds at the same

time. As mentioned earlier, most governments do provide some form of

deposit insurance because they want depositors to have confidence that

their money is safe. However, the existence of deposit insurance has the

effect of encouraging banks to reduce equity capital (thereby increasing

expected return on equity) because they no longer have to worry about

depositors losing confidence.

From the government's perspective there is

therefore a risk that the existence of deposit insurance leads to more bank

This is an example of what insurance companies term moral hazard. The existence of an

insurance contract changes the behavior of the insured party. We will discuss moral

hazard further in Chapter 14.

168

Chapter 7

failures and an increase in the cost of deposit insurance programs. As a

result governments have found it necessary to combine deposit insurance

with regulations on the capital banks must hold. In addition, govern-

ments are concerned about what is termed systemic risk. This is discussed

in Business Snapshot 7.1.

7.2 PRE-1988

Prior to 1988 bank regulators in different countries tended to regulate

bank capital by setting minimum levels for the ratio of capital to total

assets. However, definitions of capital and the ratios considered accept-

able varied from country to country. Some countries enforced their

regulations more diligently than others. Banks were competing globally

and a bank operating in a country where capital regulations were slack

was considered to have a competitive edge over one operating in a country

with tighter more strictly enforced capital regulations. In addition the

huge exposures of the major international banks to less developed

countries such as Mexico, Brazil, and Argentina and the accounting

games sometimes used to manage those exposures were starting to raise

questions about the adequacy of capital levels.

Another problem was that the types of transactions entered into by

banks were becoming more complicated. The over-the-counter derivatives

market for products such as interest rate swaps, currency swaps, and

foreign exchange options was growing fast. These contracts increase the

credit risks being taken by a bank. Consider, for example, an interest rate

swap. If the counterparty in an interest rate swap transaction defaults

Business Snapshot 7.1 Systemic Risk

Systemic risk is the risk that a default by one financial institution will create a

"ripple effect" that leads to defaults by other financial institutions and

threatens the stability of the financial system. The financial system has survived

defaults such as Drexel in 1990 and Barings in 1995 very well, but regulators

continue to be concerned. There are huge numbers of over-the-counter trans-

actions between banks. If Bank A fails, Bank B may take a huge loss on the

transactions it has with Bank A. This in turn could lead to Bank B failing,

Bank C that has many outstanding transactions with both Bank A and Bank

B might then take a large loss and experience severe financial difficulties, and

so on.

Bank Regulation and Basel II 169

when the swap has a positive value to the bank and a negative value to the

counterparty, the bank loses money. Many of these newer transactions

were "off balance sheet". This means that they had no effect on the level of

assets reported by a bank. As a result, they had no effect on the amount of

capital the bank was required to keep. It became apparent to regulators

that total assets was no longer a good indicator of the total risks being

taken. A more sophisticated approach than that of setting minimum levels

for the ratio of capital to total balance sheet assets was needed.

These problems led supervisory authorities for Belgium, Canada,

France, Germany, Italy, Japan, Luxembourg, the Netherlands, Sweden,

Switzerland, the United Kingdom, and the United States to form the

Basel Committee on Banking Supervision. They met regularly in Basel,

Switzerland, under the patronage of the Bank for International Settle-

ments. The first major result of these meetings was a document entitled

"International Convergence of Capital Measurement and Capital Stand-

ards". This was referred to as "The 1988 BIS Accord" or just "The

Accord". More recently it has come to be known as Basel I.

7.3 THE 1988 BIS ACCORD

The 1988 BIS Accord was the first attempt to set international risk-based

standards for capital adequacy. It has been subject to much criticism as

being too simple and somewhat arbitrary. In fact, the Accord was a huge

achievement. It was signed by all 12 members of the Basel Committee and

paved the way for significant increases in the resources banks devote to

measuring, understanding, and managing risks.

The BIS Accord defined two minimum standards for meeting acceptable

capital adequacy requirements. The first standard was similar to that

existing prior to 1988 and required banks to have an assets-to-capital

multiple of at most 20. The second standard introduced what became

known as the Cooke ratio. For most banks there was no problem in

satisfying the capital multiple rule. The Cooke ratio was the key regulatory

requirement.

The Cooke Ratio

In calculating the Cooke ratio both On-balance-sheet and off-balance-

sheet items are considered. They are used to calculate what is known as

the bank's total risk-weighted assets (also sometimes referred to as the

risk-weighted amount). It is a measure of the bank's total credit exposure.