Hull J.C. Risk management and Financial institutions
Подождите немного. Документ загружается.

190
Chapter 7
monitor and ensure compliance with regulatory capital ratios.
Supervisors should take appropriate supervisory action if they are
not satisfied with the result of this process.
3. Supervisors should expect banks to operate above the minimum
regulatory capital and should have the ability to require banks to
hold capital in excess of this minimum.
4. Supervisors should seek to intervene at an early stage to prevent
capital from falling below the minimum levels required to support
the risk characteristics of a particular bank and should require rapid
remedial action if capital is not maintained or restored.
The Basel Committee suggests that regulators pay particular attention to
interest rate risk in the banking book, credit risk, and operational risk.
Key issues in credit risk are stress tests used, default definitions used,
credit risk concentration, and the risks associated with the use of col-
lateral, guarantees, and credit derivatives.
The Basel Committee also stresses that there should be transparency
and accountability in the procedures used by bank supervisors. This is
particularly important when a supervisor exercises discretion in the pro-
cedures used or sets capital requirements above the minimum specified in
Basel II.
7.11 MARKET DISCIPLINE
Pillar 3 of Basel II is concerned with market discipline. The Basel
Committee wants to encourage banks to increase disclosure to the market
of their risk assessment procedures and capital adequacy. The extent to
which regulators can force banks to increase disclosure varies from
jurisdiction to jurisdiction. However, banks are unlikely to ignore direc-
tives on this from their supervisors, given the potential of supervisors to
make their life difficult. Also, in some instances, banks will have to
increase their disclosure in order to be allowed to use particular meth-
odologies for calculating capital.
Regulatory disclosures are likely to be different in form from account-
ing disclosures and need not be made in annual reports. It is largely left
to the bank to choose disclosures that are material and relevant. Among
the items that banks should disclose are:
1. The entities in the banking group to which Basel II is applied and
adjustments made for entities to which it is not applied
Bank Regulation and Basel II 191
2. The terms and conditions of the main features of all capital
instruments
3. A list of the instruments constituting Tier 1 capital and the amount
of capital provided by each item
4. The total amount of Tier 2 and Tier 3 capital
5. Capital requirements for credit, market, and operational risk
6. Other general information on the risks to which a bank is exposed
and the assessment methods used by the bank for different
categories of risk
7. The structure of the risk management function and how it operates
SUMMARY
This chapter has provided an overview of capital requirements for banks
throughout the world. The way in which regulators calculate the mini-
mum capital a bank is required to hold has changed dramatically since
the 1980s. Prior to 1988, regulators determined capital requirements by
specifying minimum ratios for capital to assets or maximum ratios for
assets to capital. In the late 1980s, both bank supervisors and the banks
themselves agreed that changes were necessary. Off-balance-sheet deriva-
tives trading was increasing fast. In addition, banks were competing
globally and it was considered important to create a level playing field
by making regulations uniform throughout the world.
The 1988 Basel Accord assigned capital for credit risk both on and off
the balance sheet. This involved calculating a risk-weighted asset for each
item. The risk-weighted asset for an On-balance-sheet loan was calculated
by multiplying the principal by a risk weight for the counterparty. In the
case of derivatives such as swaps, banks were first required to calculate a
credit equivalent amount. The risk-weighted asset was obtained by multi-
Plying the credit equivalent amount by a risk weight for the counterparty.
Banks were required to keep capital equal to 8% of the total risk-weighted
assets. In 1995 the capital requirements for credit risk were modified to
incorporate netting.
In 1996, the Accord was modified to include a capital charge for market
risk. Sophisticated banks could base the capital charge on a value-at-risk
calculation. In 1999, the Basel Committee proposed significant changes,
which are expected to be implemented in 2007. The capital for market risk
is unchanged. Credit risk capital will be calculated in a more sophisticated
192
Chapter 7
way that will reflect either (a) credit ratings from agencies such as Moody's
or S&P or (b) a bank's own internal estimates of default probabilities. In
addition, there will be a capital requirement for operational risk.
FURTHER READING
Bank for International Settlements, "Basel II: International Convergence of
Capital Measurement and Capital Standards: A Revised Framework,"
November 2005, www.bis.org.
Crouhy, M., D. Galai, and R. Mark, Risk Management. New York: McGraw-
Hill, 2001.
Gordy, M.B., "A Risk-factor Model Foundation for Ratings-Based Bank
Capital Ratios," Journal of Financial Intermediation, 12 (2003): 199-232.
Lopez, J. A., "The Empirical Relationship Between Average Asset Correlation,
Firm Probability of Default, and Asset Size," Journal of Financial
Intermediation, 13, No. 2 (2004): 265-283.
Vasicek, O., "Probability of Loss on a Loan Portfolio," Working Paper, KMV,
1987. [Published in Risk in December 2002 under the title "Loan Portfolio
Value".]
QUESTIONS AND PROBLEMS (Answers at End of Book)
7.1. "When a steel company goes bankrupt, other companies in the same
industry benefit because they have one less competitor. But when a bank
goes bankrupt, other banks do not necessarily benefit." Explain this
statement.
7.2. "The existence of deposit insurance makes it particularly important for
there to be regulations on the amount of capital banks hold." Explain this
statement.
7.3. As explained in Section 2.3 an interest rate swap involves the exchange of a
fixed rate of interest for a floating rate of interest with both being applied to
the same principal. The principals are not exchanged. What is the nature of
the credit risk for a bank when it enters into a five-year interest rate swap
with a notional principal of $100 million? Assume the swap is worth zero
initially.
7.4. In a currency swap, interest on a principal in one currency is exchanged for
interest on a principal in another currency. The principals in the two
currencies are exchanged at the end of the life of the swap. Why is the
credit risk on a currency swap greater than that on an interest rate swap?
Bank Regulation and Basel II 193
7.5. An interest rate swap currently has a negative value to a financial
institution. Is the financial institution exposed to credit risk on the trans-
action? Explain your answer.
7.6. Estimate the capital required under Basel I for a bank that has the following
transactions with a corporation (assume no netting): (a) a 9-year interest
rate swap with a notional principal of $250 million and a current market
value of — $2 million; (b) a 4-year interest rate swap with a notional
principal of $100 million and a current value of $3.5 million; and (c) a
6-month derivative on a commodity with a principal of $50 million that is
currently worth $1 million.
7.7. What is the capital required in Problem 7.6 under Basel I assuming that
the 1995 netting amendment applies?
7.8. All the contracts a bank has with a corporate client are loans to the client.
What is the value to the bank of netting provisions in the loan agreement?
7.9. Explain why the final stage in the Basel II calculations for credit risk,
market risk, and operational risk is to multiply by 12.5.
7.10. What is the difference between the trading book and the banking book for
a bank? A bank currently has a loan of $10 million dollars to a corporate
client. At the end of the life of the loan the client would like to sell debt
securities to the bank instead of borrowing. How does this change affect
the nature of the bank's regulatory capital calculations?
7.11. Under Basel I, banks do not like lending to highly creditworthy companies
and prefer to help them issue debt securities. Why is this? Do you expect
the banks' attitude to this type of lending to change under Basel II?
7.12. What is regulatory arbitrage?
7.13. Equation (7.8) gives the formula for the capital required under Basel II.
It involves four terms being multiplied together. Explain each of these
terms.
7.14. Explain the difference between the simple and the comprehensive
approach for adjusting for collateral.
7.15. Explain the difference between the standardized approach, the IRB
approach, and the advanced IRB approach for calculating credit risk
capital under Basel II.
7.16. Explain the difference between the basic indicator approach, the stand-
ardized approach, and the advanced measurement approach for calculat-
ing operational risk capital under Basel II.
7.17. Suppose that the assets of a bank consist of $200 of retail loans (not
mortgages). The PD is 1% and the LGD is 70%. What is the risk-
weighted assets under the Basel II IRB approach? How much Tier 1
and Tier 2 capital is required.
194
Chapter 7
ASSIGNMENT QUESTIONS
7.18. Why is there an add-on amount in Basel I for derivatives transactions?
"Basel I could be improved if the add-on amount for a derivatives trans-
action depended on the value of the transaction." How would you argue
this viewpoint?
7.19. Estimate the capital required under Basel I for a bank that has the following
transactions with another bank (assume no netting): (a) a 2-year forward
contract on a foreign currency, currently worth $2 million, to buy foreign
currency worth $50 million; (b) a long position in a 6-month option on the
S&P 500 with a principal of $20 million and a current value of $4 million;
and (c) a 2-year swap involving oil with a principal of $30 million and a
current swap value of -$5 million. What difference does it make if the
netting amendment applies?
7.20. A bank has the following transaction with an AA-rated corporation:
(a) a 2-year interest rate swap with a principal of $100 million worth
$3 million; (b) a 9-month foreign exchange forward contract with a
principal of $150 million worth -$5 million; and (c) a 6-month long
option on gold with a principal of $50 worth $7 million. What is the
capital requirement under Basel I if there is no netting? What difference
does it make if the netting amendment applies? What is the capital
required under Basel II when the standardized approach is used?
7.21. Suppose that the assets of a bank consist of $500 million of loans to
BBB-rated corporations. The PD for the corporations is estimated as
0.3%. The average maturity is 3 years and the LGD is 60%. What is the
risk-weighted assets for credit risk under the Basel II advanced IRB
approach? How much Tier 1 and Tier 2 capital is required. How does this
compare with the capital required under the Basel II standardized approach
and under Basel I?

The VaR Measure
In Chapter 3 we examined measures such as delta, gamma, and vega for
describing different aspects of the risk in a portfolio of derivatives. A
financial institution usually calculates each of these measures each day for
every market variable to which it is exposed. Often there are hundreds, or
even thousands, of these market variables. A delta-gamma-vega analysis
therefore leads to a huge number of different risk measures being
produced each day. These risk measures provide valuable information
for a trader who is responsible for managing the part of the financial
institution's portfolio that is dependent on a particular market variable.
However, they do not provide a way of measuring the total risk to which
the financial institution is exposed.
Value at risk (VaR) is an attempt to provide a single number that
summarizes the total risk in a portfolio of financial assets. It was
pioneered by J.P. Morgan (see Business Snapshot 8.1), and it has become
widely used by corporate treasurers and fund managers as well as by
financial institutions. As we saw in Chapter 7, the VaR measure is used
by the Basel Committee in setting capital requirements for banks
throughout the world.
In this chapter we explain the VaR measure and discuss its strengths
and weaknesses. We also cover back testing and stress testing. In the next
two chapters we will explain the two main approaches for estimating VaR
for market risk. In Chapter 12 we will consider how VaR can be estimated
for credit risk.

196
Chapter 8
8.1 DEFINITION OF VaR
When using the value-at-risk measure, we are interested in making a
statement of the following form:
We are X percent certain that we will not lose more than V dollars in the
next N days.
Business Snapshot 8.1 Historical Perspectives on VaR
J.P. Morgan is credited with helping to make VaR a widely accepted measure.
The Chairman, Dennis Weatherstone, was dissatisfied with the long risk
reports he received every day. These contained a huge amount of detail on
the Greek letters for different exposures, but very little that was really useful to
top management. He asked for something simpler that focused on the bank's
total exposure over the next 24 hours measured across the bank's entire trading
portfolio. At first his subordinates said this was impossible, but eventually
they adapted the Markowitz portfolio theory (see Section 1.1) to develop a
VaR report. This became known as the 4:15 report because it was placed on
the chairman's desk at 4:15 p.m. every day after the close of trading.
Producing the report entailed a huge amount of work involving the collec-
tion of data daily on the positions held by the bank around the world, the
handling of different time zones, the estimation of correlations and volatilities,
and the development of computer systems. The work was completed in about
1990. The main benefit of the new system was that senior management had a
better understanding of the risks being taken by the bank and were better able
to allocate capital within the bank. Other banks had been working on similar
approaches for aggregating risks and by 1993 VaR was established as an
important risk measure.
Banks usually keep the details about the models they develop internally a
secret. However, in 1994 J.P. Morgan made a simplified version of their own
system, which they called RiskMetrics, available on the internet. RiskMetrics
included variances and covariances for a very large number of different market
variables. This attracted a lot of attention and led to debates about the pros and
cons of different VaR models. Software firms started offering their own VaR
models, some of which used the RiskMetrics database. After that, VaR was
rapidly adopted as a standard by financial institutions and some nonfinancial
institutions. The BIS Amendment, which was based on VaR (see Section 7.6),
was announced in 1996 and implemented in 1998. Later the RiskMetrics group
within J.P. Morgan was spun off as a separate company. This company
developed CreditMetrics for handling credit risks in 1997 and Corporate-
Metrics for handling the risks faced by nonfinancial corporations in 1999.

The VaR Measure 197
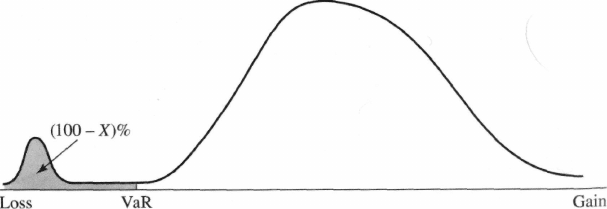
The variable V is the VaR of the portfolio. It is a function of two
parameters: the time horizon (N days) and the confidence level (X%). It
is the loss level over N days that we are X% certain will not be exceeded.
VaR is the loss corresponding to the (100 — X)th percentile of the
distribution of the change in the value of the portfolio over the next
N days. (Gains are positive changes; losses are negative changes.) For
example, when N = 5 and X = 97, VaR is the third percentile of the
distribution of changes in the value of the portfolio over the next five
days. In Figure 8.1, VaR is illustrated for the situation where the change
in the value of the portfolio is approximately normally distributed.
Figure 8.1 shows the distribution of the portfolio's daily gain, with
losses being counted as negative gains. As mentioned, VaR is the
(100 — X)th percentile of this distribution. Instead, we can calculate the
distribution of the portfolio's daily loss, with a gain being counted as a
negative loss. VaR is the Xth percentile of this distribution.
As discussed in Section 7.6, the 1996 BIS Amendment calculates
capital for the trading book using the VaR measure with N = 10 and
X = 99. This means that it focuses on the revaluation loss over a 10-day
period that is expected to be exceeded only 1 % of the time. The capital it
requires the bank to hold is k times this VaR measure (with an adjustment
for what are termed specific risks.) The multiplier k is chosen on a bank-
by-bank basis by the regulators and must be at least 3.0. For a bank with
excellent well-tested VaR estimation procedures, it is likely that k will be
set equal to the minimum value of 3.0. For other banks it may be higher.
As we will discuss in Section 8.6, when tests show a bank's VaR model
would not have performed well during the last 250 days, k may be as high
as 4.0.
Figure 8.1 Calculation of VaR from the probability distribution of the change
in the portfolio value; confidence level is X%.
198
Chapter 8
8.2 VaR vs. EXPECTED SHORTFALL
VaR is an attractive measure because it is easy to understand. In essence,
it asks the simple question: "How bad can things get?" This is the
question all senior managers want answered. They are very comfortable
with the idea of compressing all the Greek letters for all the market
variables underlying a portfolio into a single number. VaR is also
relatively easy to back test, as we shall see later in this chapter.
However, when VaR is used in an attempt to limit the risks taken by a
trader, it can lead to undesirable results. Suppose that a bank tells a
trader that the one-day 99% VaR of the trader's portfolio must be kept at
less than $10 million. The trader can construct a portfolio where there is
a 99% chance that the daily loss is less than $10 million and a 1% chance
that it is $500 million. The trader is satisfying the risk limits imposed by
the bank but is clearly taking unacceptable risks.
This behavior by a trader is not as unlikely as it sounds. Many traders
like taking high risks in the hope of realizing high returns. If they can find
ways of taking high risks without violating risk limits, they will do so. To
quote one trader the author has talked to: "I have never met a risk control
system that I cannot trade around." The problem we are talking about is
summarized by Figures 8.1 and 8.2. The figures show the probability
distribution for the gain or loss on a portfolio during N days. Both
portfolios have the same VaR, but the portfolio in Figure 8.2 is much
riskier than that in Figure 8.1 because expected losses are much larger.
Expected Shortfall
A measure that produces better incentives for traders than VaR is expected
shortfall. This is also sometimes referred to as conditional VaR or tail loss.
Figure 8.2 Alternative situation to Figure 8.1; VaR is the same, but the
potential loss is larger.

The VaR Measure
199
Whereas VaR asks how bad can things get, expected shortfall asks: "If
things do get bad, what is the expected loss?" Expected shortfall, like VaR,
is a function of two parameters: N (the time horizon in days) and X (the
percent confidence level). It is the expected loss during an N-day period
conditional on the loss being greater than the Xth percentile of the loss
distribution.
1
For example, with X = 99 and N = 10, the expected short-
fall is the average amount we lose over a ten-day period assuming that the
loss is greater than the 99th percentile of the loss distribution.
As we show in the next section, expected shortfall has better properties
than VaR in that it encourages diversification. One disadvantage is that it
does not have the simplicity of VaR and, as a result, is slightly more
difficult to understand. Another is that it is more difficult to back test.
VaR has become the most popular measure of risk among both regulators
and risk managers in spite of its weaknesses. Therefore, in most of our
discussions in this chapter and the next two, we will focus on how VaR can
be measured and used. Many of the points we make apply equally to
expected shortfall and other risk measures.
8.3 PROPERTIES OF RISK MEASURES
A risk measure used for specifying capital requirements can be thought of
as the amount of cash (or capital) that must be added to a position to make
its risk acceptable to regulators. Artzner et al. have proposed a number of
properties that such a risk measure should have.
2
These are:
1. Monotonicity: If a portfolio has lower returns than another portfolio
for every state of the world, its risk measure should be greater.
2. Translation invariance: If we add an amount of cash K to a portfolio,
its risk measure should go down by K.
3. Homogeneity: Changing the size of a portfolio by a factor while
keeping the relative amounts of different items in the portfolio the same
should result in the risk measure being multiplied by
4. Subadditivity: The risk measure for two portfolios after they have been
merged should be no greater than the sum of their risk measures before
they were merged.
1
As mentioned earlier, gains are calculated as negative losses, and so all outcomes are
considered when a loss distribution is constructed.
See P. Artzner, F. Delbaen, J.-M. Eber, and D. Heath, "Coherent Measures of Risk,"
Mathematical Finance, 9 (1999): 203-228.
