Hooke R.L. Principles of glacier mechanics

Подождите немного. Документ загружается.

Stresses, strains, and strain rates 11

(

)

n (

−

)

n (

−

)

(

)

Figure 2.3. Sign convention

for stresses in plane strain.

Similarly, if a shear stress, σ

,isinthe positive x-direction on a

plane on which

n is positive, that shear stress is considered to be positive

and conversely. By this deﬁnition both shear stresses σ

and σ

in the

diagram are positive.

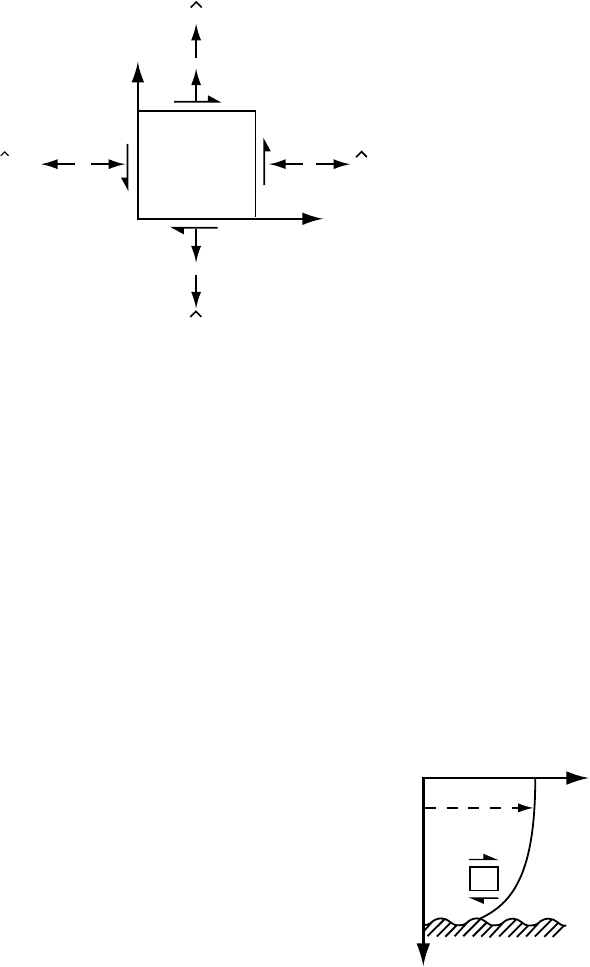
As an example, consider the variation of u with depth in a glacier

(Figure 2.4). As depicted by the arrows around the box in Figure 2.4, the

shear stress, σ

,isnegative in the coordinate system shown. The veloc-

ity derivative, du/dz,isalso negative (u decreases with increasing z).

Thus the negative shear stress results in a negative strain rate, as one

would expect.

bed

Figure 2.4. Vertical proﬁle

of horizontal velocity, u.

Sense of shear stress, σ

,is

shown by arrows above and

below box.

Tensors

The three-dimensional diagram in Figure 2.5 shows stress vectors on

three faces of a cube. Similar stresses occur on the concealed faces,

but they are in the opposite directions. The cube is considered to be

inﬁnitesimal, representing, say, a point in the glacier. Thus, stresses on

any given face can be regarded as uniformly distributed and constant.

To completely describe the state of stress at this point, we need nine

stress components; thus:

This assemblage of stress vectors is called a second-rank tensor.For

comparison, to describe a ﬁrst-rank tensor, a vector, we need its compo-

nents along three coordinate axes.

12 Some basic concepts

Figure 2.5. Stresses on a

cube.

For steady (non-accelerating) uniform motion, forces must be bal-

anced. Thus, to ensure that there is no tendency for the cube in Figure 2.5

to rotate, it is necessary that σ

= σ

, σ

= σ

, and σ

= σ

. Such

tensors are called symmetric.

When a tensor is symmetric, it is common to see, for example, xy

used where, rigorously, yx might be more correct. In another common

abbreviation often encountered, σ

is written for σ

Strains and strain rates

In a deformable medium, stresses induce deformation or strain. Strain

is deﬁned as the change, ,inlength of a line divided by the initial

length of that line, 

, thus: /

. The symbol ε is commonly used

to denote strain. The rate at which strain occurs, or the strain rate, is

denoted by ˙ε. The dot superscript is commonly used to denote a time

derivative, making it a rate. As nine separate stress vectors are needed to

describe fully the state of stress at a point, so also are nine strains or strain

rates needed to describe the state of straining at that point. Thus, these

assemblages of strains and strain rates are also second-rank tensors, the

strain and strain-rate tensors. As was the case with the stress tensor, these

tensors, too, are symmetric, so ε

= ε

,˙ε

= ˙ε

, and so forth.

In Chapter 9,wewill show that:

˙ε



∂u

∂y

∂v

∂x



(2.6a)

and similarly for the other shear strain rates. When x = y, this becomes:

˙ε

∂u

∂x

(2.6b)

Stresses, strains, and strain rates 13

and so forth. Note that in terms of expressions like Equation (2.6b), the

incompressibility condition, Equation (2.5), becomes:

˙ε

+ ˙ε

= 0 (2.7)

Equations (2.6a) and (2.6b) deﬁne strain rates in terms of differences

in velocity between points that are an inﬁnitesimal distance (for exam-

ple, dx) apart. However, when measuring strains or strain rates in the

laboratory or ﬁeld, it is technically impossible to resolve differences in

velocity over “inﬁnitesimal” distances. Thus, we make measurements

over longer distances and use what is called logarithmic strain. The

quantity measured is the change in the distance between two points over

a time interval, t.Ifthe initial distance is 

and the ﬁnal distance is ,

then ˙ε is deﬁned as:

˙ε =

t



This relation will be derived in Chapter 9.

Yield stress

In some materials there is no deformation at stresses below a certain

stress, called the yield stress. The yield stress is a property of that par-

ticular material. In other materials, deformation rates are so low at low

stresses that theoretical models sometimes assume the existence of a

yield stress even though there may not actually be one. Ice is such a

material.

Deviatoric stresses

Ice does not deform in response to hydrostatic pressure alone. In other

words, in a topographic depression containing ice (Figure 2.6), the hydro-

static (or cryostatic) pressure would increase linearly with depth, z,ata

rate ρgz,where g is the acceleration due to gravity. As a rule of thumb,

the pressure increases at a rate of 0.1 MPa for every 11 m of depth. Thus,

it becomes quite high at large depths. However, if the surface of the ice

in the depression is horizontal, as in a lake, the only deformation that

would occur would be a relatively insigniﬁcant elastic compression.

On the other hand, if the ice surface slopes gently (Figure 2.6, dashed

line), and if points A and B are on a horizontal plane, then the pressure at

A would be greater than the pressure at B. This pressure difference would

result in a compressive strain between A and B. The strain rate would

depend upon the small pressure difference and not, in any signiﬁcant

way, on the much larger hydrostatic pressure at depth z.

14 Some basic concepts

Horizontal

surface

Figure 2.6. Sketch to

illustrate non-hydrostatic

pressure.

Because straining in glaciers is related to such stress differences,

it is convenient to deﬁne a stress, called the deviatoric stress or stress

deviator,which reﬂects this principle. The deviatoric normal stress in

the x-direction is:



= σ

− P (2.8)

where P is the mean normal stress:

P =

(σ

+ σ

) (2.9)

P is close to, but not necessarily equal to, the hydrostatic pressure. As

P is a normal stress, it contributes only to the normal stresses, and not

to the shear stresses in Figure 2.5.Inother words, the deviatoric shear

stresses are the same as their non-deviatoric or total counterparts, but

the deviatoric normal stresses are very different from the total normal

stresses, especially at depth.

Effective and octahedral shear stresses and strain rates

Theoretical studies and a limited amount of experimental data suggest

that the strain rate in a given direction in ice depends not only on the

stress in that direction, but also on all of the other stresses acting on the

medium. To take this into account, we deﬁne the effective shear stress,

, and the effective strain rate,˙ε

,by:

√



2

+ σ

2

+ σ

2

+ σ



1/2

(2.10)

and

˙ε

√



˙ε

+ ˙ε



1/2

(2.11)

Alternatively, some glaciologists use the octahedral shear stress, σ

, and

octahedral shear strain rate,˙ε

, deﬁned by:

√



2

+ σ

2

+ σ

2

+ σ



1/2

(2.12)

Stresses, strains, and strain rates 15

and

˙ε

√



˙ε

+ ˙ε



1/2

(2.13)

respectively.

Principal stresses and strain rates

In Chapter 9,wewill show that, at any point in a medium, it is always

possible to orient a rectangular coordinate system in such a way that

shear stresses vanish. Equation (2.12) then becomes:



+ σ



+ σ





1/2

(2.14)

We give the name principal stresses to the remaining normal stresses,

and the axes in this coordinate system are called the principal axes of

stress. Similarly, if the coordinate system is oriented such that shear

strain rates vanish, the remaining strain rates are called the principal

strain rates and the axes are the principal axes of strain rate.

Equation (2.14) shows that the octahedral shear stress is the root-

mean-square of the principal stress deviators. When the coordinate axes

are aligned parallel to the principal stresses, the octahedral shear stress

is the resolved shear stress on the octahedral plane, a plane that intersects

the three axes at points equidistant from the origin (Figure 2.7). Hence

the name: octahedral shear stress.

Octahedral

plane

Figure 2.7. A plane that

intersects the x-, y-, and

z-axes at points equidistant

from the origin, in this case

a unit distance, is called the

octahedral plane. If similar

planes are drawn involving

the negative directions

along the axes, the solid

ﬁgure formed is a regular

octahedron.

The ﬂow law

The most commonly used ﬂow law for ice is Glen’s ﬂow law, named after

John W. Glen upon whose experiments it is based (Glen, 1955). We will

normally write Glen’s ﬂow law in the form he originally used:

˙ε





(2.15)

where B is a viscosity parameter that increases as the ice becomes stiffer,

and n is an empirically determined constant. Most studies have found

that n ≈ 3. At very low stresses, however, there is some evidence that

n → 1. An alternative form of the ﬂow law that is commonly used is:

˙ε

= Aσ

(2.16)

Here, B is normally given in MPa a

1/n

,while A is in MPa

−n

−1

kPa

−n

−1

.Ifthe octahedral shear stress and strain rate are used, the

numerical values of B and A must be adjusted accordingly, but the units

stay the same.

16 Some basic concepts

Both forms of the ﬂow law have their advantages, and as A = (1/B)

it is easy to convert between the two forms as long as n is known. The

form ˙ε

= Aσ

resembles conventional constitutive relations in rheol-

ogy, and is also easier to generalize if greater precision is needed in

situations involving complicated stress conﬁgurations (Glen, 1958). For

example, some materials, when subjected to a shear stress, swell or con-

tract perpendicular to the plane of shear. In other words, deformation

occurs in directions in which the stress is zero. Such rheologies require

an extra term in the ﬂow law, and this is more readily accommodated with

aﬂowlawofthe form ˙ε

= Aσ

.Sofar, however, the forms presented

in Equations (2.16) and (2.17) seem adequate to represent phenomena

observed in studies of ice deformation, both in the laboratory and on

glaciers, so the additional term is not needed.

The form ˙ε

=(σ

/B)

is similar to that used in ﬂuid mechanics with

the viscosity, η, deﬁned by:

τ = η

(2.17)

Here τ is the shear stress. Thus B, like η,isaratio of stress to strain rate.

An increase in B results in a decrease in strain rate. Scientists interested

in geomorphological applications of glaciological principles are more

likely to be familiar with principles of ﬂuid mechanics than with those

of rheology, so the form ˙ε

= (σ

/B)

is used throughout this book.

In Chapter 9,wewill show that if the principle axes of stress and

strain rate coincide, as is normally the case, the ﬂow law can be written

as:

˙ε

n−1



(2.18)

where i and j can represent x or y or z. Eliminating σ

from Equations

(2.15) and (2.18) yields:

˙ε

n−1



(2.19)

Equation (2.18) re-emphasizes a fundamental tenet of Glen’s ﬂow law

mentioned above: namely that the strain rate in a given direction is a

function not only of the stress in that direction, but also of all of the

other stresses acting on the medium. Equation (2.19) shows that we can

express this concept in terms of strain rates, which are generally easier

to measure than stresses.

In the next several chapters we will be dealing with situations in

which it is feasible to assume that one stress so dominates all of the

others that the others can be neglected. However, the reader should be

aware of the implications of this assumption.

Chapter 3

Mass balance

Glaciers exist because there are areas, generally at high elevations or

in polar latitudes, where snow fall during the winter exceeds melt (and

other losses) during the summer. This results in net accumulation, and

this part of the glacier is thus called the accumulation area (Figure 3.1).

As each snow layer is buried, the pressure of the overlying snow

causes compaction, and movement of molecules in the liquid and vapor

phases results in snow metamorphism. Snow that is more than a year

old, and has thus been altered by these processes, is called ﬁrn. The

end result of the ﬁrniﬁcation process, normally after several years, is

solid ice.

Where there are lower elevations to which this ice can move, grav-

itational forces drive it toward these areas. This eventually brings the

ice into places where the annual melt exceeds snow fall. Here, all of the

winter snow and some of the underlying ice melts during the summer.

This is called the ablation area. The line separating the accumulation

and the ablation areas at the end of a melt season is called the equilib-

rium line. Along the equilibrium line, melt during the just-completed

summer exactly equaled net snow accumulation during the previous

winter.

In this chapter, we ﬁrst discuss the transformation of snow to ice,

and show how the processes involved result in a physical and chemical

stratigraphy that, under the right circumstances, can be used to date ice

that is thousands of years old. We then explore the climatic factors that

result in changes in the altitude of the equilibrium line, and hence in

advance and retreat of glaciers.

18 Mass balance

Accumulation area

Ablation

area

Divide

Equilibrium

line

(a)

(+)

Specific

net

budget,

(

)

Accumulation

area

Equilibrium

line

Ablation

area

(b)

Specific

net

budget,

(+)

(

)

Figure 3.1. Cross sections of: (a) a typical polar ice cap or ice sheet, and (b) a

typical valley glacier, showing the relation between equilibrium line and ﬂow

lines. Sketches are schematic, but relative proportions are realistic.

The transformation of snow to ice

The ﬁrst phase of the transformation of snow into ice involves diffusion of

water molecules from the points of snow ﬂakes toward their centers; the

ﬂakes thus tend to become rounded, or spherical (Figure 3.2a), reducing

their surface area and consequently their free energy. This is an example

of an important thermodynamic principle, namely that the free energy of

a system tends toward a minimum. Such rounding occurs more rapidly

at higher temperatures.

The transformation of snow to ice 19

Trapped

air bubbles

(a)

(b)

(c)

Figure 3.2. Transformation of snow to ice. (a) Modiﬁcation of snow ﬂakes to a

subspherical form. (b) Sintering. (c) Processes during sintering: 1 = sublimation,

2 = molecular diffusion within grains, 3 = nucleation and growth of new grains,

and 4 = internal deformation of grains. (Based on Sommerfeld and LaChapelle,

1970, Figures 2, 16, and 17; and on Kinosita, 1962,asreported by Lliboutry,

1964, Figure 1.14.)

The closest possible packing of spherical particles would be one with

a porosity of about 26%, the so-called rhombohedral packing. However,

in natural aggregates of spheres of uniform diameter, the pore space is

usually closer to 40%. In the case of ﬁrn, this corresponds to a density

of ∼550 kg m

−3

Further densiﬁcation involves a process called sintering (Figure

3.2b), which involves transfer of material by sublimation and by molec-

ular diffusion within grains, nucleation and growth of new grains, and

internal deformation of the grains (Figure 3.2c). Sublimation is more

important early in the transformation process when pore spaces are still

large. Internal deformation increases in importance as the snow is buried

deeper and pressures increase. In warm areas, the densiﬁcation process

is accelerated, both because grains may be drawn together by surface

tension when water ﬁlms form around them, and because percolating

melt water may ﬁll air spaces and refreeze.

An important transition in the transformation process occurs at a

density of ∼830 kg m

−3

.Atabout this density, pores become closed,

preventing further air movement through the ice. Studies of the air thus

trapped provide information on the composition of the atmosphere at the

time of close off (see, for example, Raynaud et al., 1993). Measurements

of the volume of such air per unit mass of ice yield estimates (albeit fairly

crude, given present technology) of the altitude of the pores at the time

20 Mass balance

Accumulation area

Ablation

area

Dry-snow line

Wet-snow line

Percolation

zone

Surface at end

of summer

Snow

line

Equilibrium

line

Maximum surface

height in current

year

Maximum height

of superimposed

ice

Superimposed

ice zone

C isotherm

at end of summer

Surface at end of

previous summer

Snow

Snow with ice layers and lenses

Superimposed ice

Wet-snow

zone

Dry-

snow

zone

Figure 3.3. Variation in snow facies with altitude. (After Benson, 1962.)

Horizontal distance from equilibrium line to dry-snow line is tens to hundreds

of kilometers.

of close off (Martinerie et al., 1992). Knowing the depth in the glacier

at which this occurs then permits an estimate of the elevation of the ice

surface at that time. Pore close off can occur at depths of tens to over a

hundred meters, depending on temperature (Paterson, 1994,Table 2.2).

Snow stratigraphy

At high elevations on polar glaciers, such as the Antarctic or Greenland

ice sheets, there are areas where no melting occurs during the sum-

mer. At somewhat lower elevations, some melting does occur, and the

meltwater thus formed percolates downward into the cold snow where it

refreezes, forming lenses or gland-like structures. The higher of these two

zones is called the dry-snow zone and the lower is the percolation zone

(Figure 3.3) (Benson, 1961;M¨uller, 1962). In keeping with stratigraphic

terminology in geology, parts of the annual snow pack on an ice sheet

that have distinctive properties are referred to as facies –inthis case

the dry-snow facies and the percolation facies, respectively. The bound-

ary between these two zones or facies, the dry-snow line, lies approxi-

mately at the elevation where the mean temperature of the warmest month

is −6

◦

C (Benson, 1962, cited by Loewe, 1970,p.263).

At lower elevations, summer melting is sufﬁcient to wet the entire

snow pack. This is called the wet-snow zone (Figure 3.3). When this snow

refreezes, a ﬁrm porous layer is formed. In downglacier parts of this zone,

the basal layers of the snow pack may become saturated with water. If the