Hooke R.L. Principles of glacier mechanics

Подождите немного. Документ загружается.

Chapter 10

Stress and velocity distribution in an

idealized glacier

Let us now use Equations (9.32) to calculate stresses and velocities in an

idealized glacier consisting of a slab of ice of inﬁnite horizontal extent

resting on a bed with a uniform slope. By appropriate choice of the

coordinate system, the problem is thus reduced to two dimensions, or

plane strain. The ice is assumed to be isotropic and incompressible. We

will consider ﬁrst the case of a perfectly plastic rheology. Then a more

realistic nonlinear ﬂow law is used. Our discussion is based on papers

of Nye (1951, 1957), which are classics in glaciology.

Although glaciers consisting of such slabs are uncommon, to say

the least, there are several reasons for undertaking this calculation. First,

it provides an opportunity to apply some of the material discussed in

the previous chapter. Secondly, the stress distributions are representa-

tive of those which we expect to ﬁnd in glaciers, and are commonly used

approximations when the required assumptions can be justiﬁed by the

geometry of a problem. Thirdly, the calculations demonstrate the limi-

tations of analytical methods in situations in which boundary conditions

are complex. For calculations involving glaciers with realistic shapes,

numerical models are required for all but the simplest situations. Finally,

the effect of longitudinal stresses on velocity proﬁles is elucidated.

Solutions for stresses and velocities in plane strain

The coordinate system to be used for the calculation is shown in

Figure 10.1: x is parallel to the glacier surface in the direction of ﬂow and

z is directed downward normal to the surface. The origin is on the surface

271

272 Stress and velocity distribution

Glacier surface

Bed

Figure 10.1. Coordinate

system used in calculating

stresses and velocities in plane

strain.

of the slab, which has a thickness h. The velocities are u, v, and w in the

x-, y-, and z-directions, respectively.

In our discussion of plane strain in Chapter 9,wetook ˙ε

to be 0, but

here our choice of coordinate axes makes ˙ε

=0, so σ



= 0. Therefore,

as in Equations (9.12) and (9.13):

= P =

(

+ σ

)

(10.1)

Also:

= 0

ν = 0

(10.2)

Equations (10.1) and (10.2) are four of the equations needed to solve for

the three normal stresses, three shear stresses, and three velocities, so

we need ﬁve more from Equations (9.32). These are:

∂σ

∂x

∂σ

∂z

+ ρg

= 0 (10.3)

∂σ

∂x

∂σ

∂z

+ ρg

= 0

(10.4)

∂u

∂x

= λσ



= λ(σ

− P) = λ



−

(σ

+ σ

)



(σ

− σ

) (10.5)

and similarly

∂w

∂z

=−

(σ

− σ

) (10.6)

and



∂u

∂z

∂w

∂x



= λσ

(10.7)

Note that ∂u/∂x =−∂w/∂z as required by the incompressibility condi-

tion in plane strain (Equation (2.5)).

Because λ = f (σ )/σ ,wehavetointroduce an expression for σ ,

namely:

(σ

− σ

)

+ σ

(10.8)

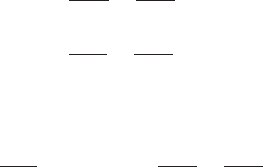
Solutions for stresses and velocities 273

(see discussion following Equation (9.14)) which, as we have seen, can

be derived from the von Mises yield criterion in plane strain, and is, in

fact, the effective stress in plane strain. Still needed is an expression for

f (σ ); this will be based on the speciﬁc ﬂow law chosen for any given

solution.

Stress solutions in a perfectly plastic medium

Suppose our slab is composed of perfectly plastic “ice”. Suppose, further,

that accumulation and ablation are occurring on the surface of the slab,

but that it is in a steady state so the proﬁle does not change. Thus, it must

be deforming to accommodate the addition or loss of mass. In order to

avoid a discontinuity at depth, the deformation must extend throughout

the slab. Furthermore, in a deforming perfectly plastic material, the stress

must reach but cannot exceed the yield stress, k (Chapter 9). Therefore,

σ = k everywhere.

Near the bed, although a small uniform longitudinal strain rate is

present, deformation is principally by simple shear. Because any ten-

dency toward an increase in stress above k is absorbed by more rapid

deformation in a perfectly plastic material, ˙ε

→∞at the bed. Thus,

˙ε

is the dominant term in ˙ε,soσ

is the dominant term in σ (Equation

(10.8)), and σ

must approach σ (= k)atthe bed. Therefore, we adopt

the following boundary conditions:

=−k on z = h (bed)

= 0,σ

= 0onz = 0 (surface)

Here σ

and σ

are 0 at the surface because atmospheric pressure is a

hydrostatic pressure that can be neglected and because there can be no

traction on a free surface, respectively. Note that σ

is set equal to −k on

the bed because the drag exerted on the ice by the bed is in the negative

x-direction. Because σ

is independent of x on the bed, we will seek a

solution in which σ

is independent of x everywhere.

The following solution, previously unpublished, is contained in a

manuscript by J. F. Nye that he kindly provided to the present author, and

is used with his permission. We take the derivative of Equation (10.3)

with respect to z and of Equation (10.4) with respect to x, thus:

∂

∂z∂ x

∂

∂z

= 0

∂

∂x∂ z

∂

∂x

= 0

(10.9)

As σ

and σ

are continuous functions, the order of differentiation can

be reversed in the ﬁrst of these equations. Subtracting then yields:

∂

∂x∂ z

(σ

− σ

) =



∂

∂x

−

∂

∂z



(10.10)

274 Stress and velocity distribution

Substituting for σ

− σ

from Equation (10.8) and setting σ = k as

noted above, we ﬁnd:

∂

∂x∂ z





− σ





∂

∂x

−

∂

∂z



(10.11)

Making use of the condition that σ

is independent of x allows us to

simplify this to:

∂

∂z

= 0 (10.12)

which has the solution:

= c

z + c

(10.13)

To satisfy the boundary condition σ

= 0onz = 0, we ﬁnd that c

= 0.

The boundary condition σ

=−k on z = h then yields c

=−k/h. Thus

the solution for σ

becomes:

=−

(10.14)

In other words, the shear stress varies linearly with depth.

Using this solution for σ

in Equations (10.3) and (10.4) yields:

∂σ

∂x

− ρg

∂σ

∂z

=−ρg

which integrate to:

− ρg

x + f

(z)

=−ρg

z + f

(x )

(10.15)

where f

(z) and f

(x) are functions that are dependent only upon z and x,

respectively, so that ∂f

(z)/∂x =0 and ∂f

(x)/∂z =0. They are analogous

to the constants of integration in Equation (10.13), and must be evaluated

with the use of the boundary conditions. Substituting these solutions

for σ

, σ

and σ

back into Equation (10.8), the yield criterion, we

obtain:

− ρg

x + f

(z) + ρg

z − f

(x ) =±2



−

which is true for all x and z because, as noted, the yield criterion must be

met throughout the slab. Thus, collecting the terms in x on the left-hand

side and those in z on the right results in:

− ρg

x − f

(x ) =−ρg

z ± 2k



1 −





− f

(z) = c (10.16)

Solutions for stresses and velocities 275

Because the left-hand side is a function of x alone and the right-hand

side is a function of z alone, the two sides can be equal to each other in

the general case only if each, individually, is equal to the same constant,

c,asshown. We can thus solve Equation (10.16) for f

(x)interms of c,

and for f

(z)interms of c. These solutions are then inserted in Equations

(10.15)toyield:

− ρg

x − ρg

z ± 2k



1 −





− c

=−ρg

z +

− ρg

x − c

(10.17)

Making use of the boundary condition σ

= 0onz = 0inthe second of

Equations (10.17)gives:

c =

− ρg

x = x



− ρg



As this must hold for all x,itisclear that k/h − ρg

must equal 0, and

therefore c must also be 0. Thus:

= ρg

This implies that the block must have some critical thickness, h = k/ρg

Using these results in Equations (10.17), and repeating Equation (10.14),

allows us to write the complete stress solutions thus:

=−ρg

z ± 2k



1 −





=−ρg

z (10.18)

=−

As a check on these solutions, they may be substituted back into the yield

criterion, Equation (10.8), to show that σ = k.

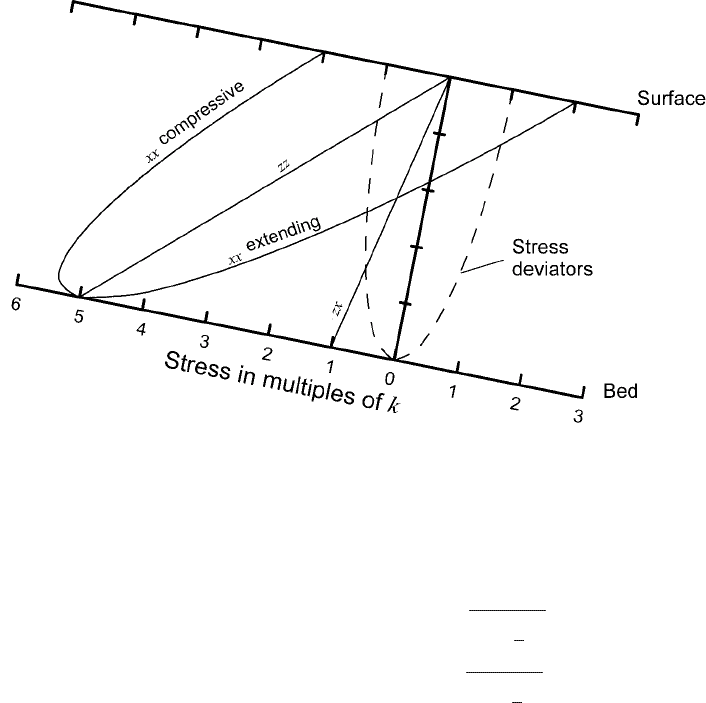
A plot (Figure 10.2) will serve to illustrate the solutions. Scaling σ

by k (= ρg

h) results in:

=−

cos α

sin α

is 0 at the surface and it decreases linearly with depth. With

tan α = 1/5, we ﬁnd that σ

=−5k on z = h (Figure 10.2). Simi-

larly, σ

=±2k on z = 0 and since σ

= σ

on the bed σ

=−5k

there. In this case, however, the distribution with depth is elliptic. Finally,

also decreases linearly with depth to −k on the bed.

The deviatoric stresses can also be calculated. Noting that:

P =

(

+ σ

)

=−ρg

z ± k



1 −





276 Stress and velocity distribution

−

Figure 10.2. Depth variation of stress in a deforming slab of material with a

perfectly plastic rheology. The slab is of uniform thickness and density, and is

resting on a bed with a uniform slope. (Modiﬁed from Nye, 1951, Figure 2c.

Reproduced with permission of the author and the Royal Society of London.)

we ﬁnd that:



= σ

− P =±k



1 −







= σ

− P =∓k



1 −





(10.19)

so σ



is ±k at the surface and decreases to 0 at the bed, as shown by

the dashed lines describing a semi-ellipse in Figure 10.2.Asrequired by

continuity, σ



=−σ



; that is, if our medium is homogeneous, isotropic,

and incompressible, as assumed, a deformation in the x-direction, ˙ε

caused by a stress σ



must be accompanied by an equal deformation of

opposite sign, ˙ε

,inthe z-direction, and this requires a stress equal to



,but in the opposite direction.

Negative or compressive deviatoric stresses in the x-direction result

in longitudinal compression, and this ﬂow regime is thus referred to as

compressive ﬂow. Similarly, positive deviatoric stresses in the x-direction

result in what is called extending ﬂow. The former is characteristic of

ablation zones of glaciers, where melt must be replaced by upward ﬂow

of ice, and the latter is characteristic of accumulation zones.

Solutions for stresses and velocities 277

(a)

(b)

Figure 10.3. Slip line ﬁelds

in a deforming slab of

material with a perfectly

plastic rheology. (a) Extending

ﬂow, and (b) compressive

ﬂow. (Modiﬁed from Nye,

1951, Figure 5.)

It is also of interest to examine the orientation of the principal stresses

and of the maximum shear stresses. In Chapter 9 (Equation (9.3b)) we

found that:

tan 2θ =

2σ

(

− σ

)

so:

θ =

tan

−1

−2kz/ h

±2k



1 −





tan

−1



∓

√

− z



On z =0, θ =0

◦

or 90

◦

and on z =h, θ =45

◦

or 135

◦

. Thus at the surface,

the principal stresses are parallel and normal to the surface, and at the

bed, they make an angle of 45

◦

or 135

◦

with the bed. The former could

also be deduced from the fact that there is no shear traction on a free

surface, so the stresses parallel and normal to this surface are principal

stresses. The orientation of the planes of maximum shear stress may be

found by differentiating Equation (9.2) with respect to θ (replacing y by z)

and setting the result equal to 0, thus:

tan

−1



√

− z



In this case, θ

=±45

◦

at the surface and 0

◦

or 90

◦

at the bed. (Thus,

the planes of maximum shear stress make an angle of 45

◦

with respect to

the principal stresses.) At any intermediate depth there are two solutions

for θ

that are 90

◦

apart. Thus, the loci of the zones of maximum shear

stress are as shown in Figure 10.3. This is what is known as the slip line

ﬁeld for the particular stress conﬁguration.

278 Stress and velocity distribution

Velocity solutions in a perfectly plastic medium

We now use the stress solutions, Equations (10.18), to obtain solutions

for the velocities from Equations (10.5) through (10.7). From Equations

(10.5) and (10.6)weobtain:

∂u

∂x

=−

∂w

∂z

(

− σ

)

(10.20)

=±λk



1 −





and from Equation (10.7):

∂u

∂z

∂w

∂x

= 2λσ

=−2λ

(10.21)

Let us ﬁrst examine the applicable boundary conditions. The stress

solutions are valid only for the thickness h = k/ρg

. Therefore, we seek

avelocity solution that will maintain this thickness. Because there is

accumulation, b

(or ablation, −b

)atthe surface, we know that:

w = b

on z = 0

w = 0onz= h

We will now show that ∂w/∂x = 0. The stresses are independent of

x, and the material is the limiting case of a purely viscous material in

which stresses determine strain rates. Therefore, the strain rates must be

independent of x.Inparticular, ∂w/∂z is independent of x, so:

∂

∂x



∂w

∂z



= 0

or, as w must be continuous in x and z:

∂

∂z



∂w

∂x



= 0

Therefore, ∂w/∂x = const, independent of z. Then, because ∂w/∂x = 0

on the upper and lower boundaries from the boundary conditions,

∂w/∂x = 0everywhere.

Equation (10.21)now becomes:

∂u

∂z

=−2λ

(10.22)

Combining Equations (10.20) and (10.22)toeliminate λ yields:

∂u

∂z

=±

2(kz/ h)



1 −

(

z/ h

)

∂w

∂z

(10.23)

=±

√

− z

∂w

∂z

Solutions for stresses and velocities 279

Differentiating with respect to x and again making use of the fact that w

is continuous in x and z gives:

∂

∂x∂ z

=±

√

− z

∂w

∂x∂ z

=±

√

− z

∂

∂z



∂w

∂x



= 0

where the last equality results from the fact that ∂w/∂x = 0. Thus from

Equation (10.20), differentiating with respect to z,weobtain:

∂

∂z∂ x

=−

∂

∂z

= 0 (10.24)

which has the solution:

w = c

z + c

Using the ﬁrst boundary condition, w = b

on z = 0, yields c

= b

whereupon the second boundary condition, w = 0onz = h, yields

0 =c

h +b

. The solution for the velocity in the z direction thus becomes:

w = b



1 −



(10.25)

Note that w varies linearly with depth. We discussed this in Chapter 5

(pp. 87–90) and will analyze it in greater detail later.

Using this solution for w in Equation (10.20)weobtain:

∂u

∂x

=−

∂w

∂z

(10.26)

and from Equation (10.23):

∂u

∂z

=∓

√

− z

(10.27)

In the coordinate system we have chosen, σ

is negative for positive z.

Therefore ˙ε

, and hence in Equation (10.27), ∂u/∂z, must be negative so

that a negative stress produces a negative strain rate. (In other words, the

horizontal velocity must decrease with depth.) Thus, when b

is positive

in Equation (10.27)weuse the upper sign, and conversely. Equation

(10.27) thus becomes:

∂u

∂z

=−2

√

− z

(10.28)

Integrating Equation (10.26) yields:

u =

+ f (z)

280 Stress and velocity distribution

= w

Bed

2 b

Bed

2 b

= w

(a) Accumulation area; b

positive (b) Ablalation area; b

negative

Figure 10.4. Velocity solutions for a deforming slab of material with a perfectly

plastic rheology.

where, as in Equation (10.15), f (z) represents some function of z alone.

Taking the derivative of this with respect to z, substituting the result into

Equation (10.28), and integrating gives:

f (z) = 2



− z

+ c

Thus, the solution for the velocity in the x-direction is:

u =

+ 2



− z

+ c (10.29)

These velocity solutions are illustrated in Figure 10.4.Onz = 0,

u = (b

x/h) +2

+ c and w = b

,while on z = h, u = (b

x/h) +c

and w = 0. Thus evidently (b

x/h) +c is the “sliding” speed. Note that

Equation (10.29) implies that the ice must be free to slide on the bed at

a speed determined by b

, and independent of σ

and bed roughness.

If, on the contrary, the sliding speed were presumed to be a function of

and bed roughness, the distribution of stress and hence of w could not

be independent of x, and the ice mass would not remain a uniform slab.

A reasonable presumption is that the sliding speed would not increase

sufﬁciently rapidly with x, and that conservation of mass would then

require that the ice thickness increase upglacier, leading to a convex

surface proﬁle. Depending on the degree of convexity and the consequent

change in ice thickness, such a proﬁle would offer the potential for

increasing σ

downglacier. This would provide the required increase in

mass ﬂux.

If the boundary conditions were selected such that u = 0atx = 0,

z = h, then c would be 0, but the original differential equations are