Hooke R.L. Principles of glacier mechanics

Подождите немного. Документ загружается.

Momentum balance 261

(

) (

)

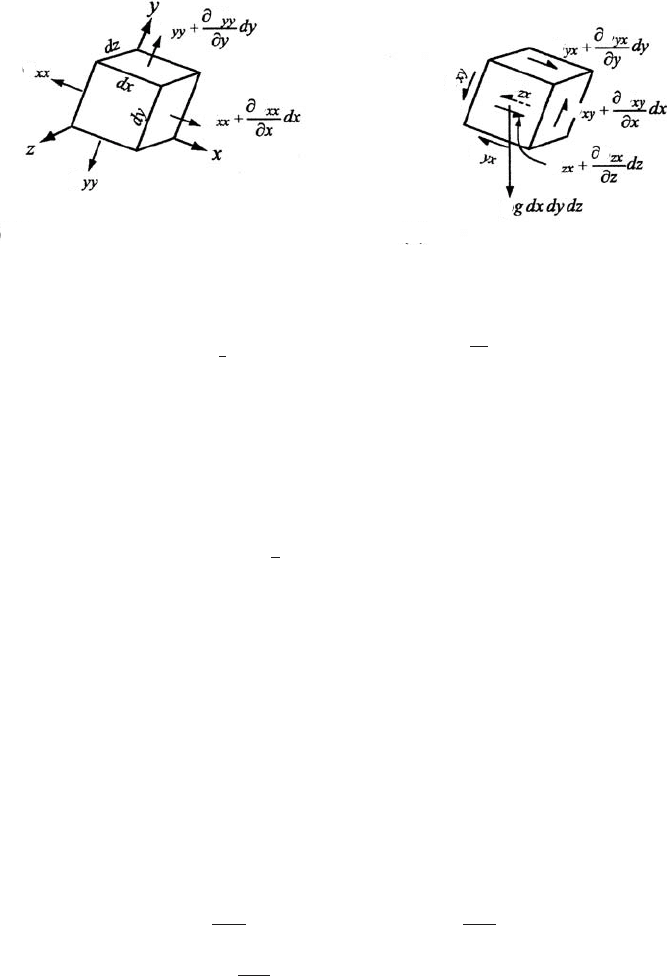
Figure 9.5. Stresses on a block of size dx dy dz. (a) Normal stresses. (b) Shear

stresses (in the x-direction only).

from Equation (9.14) that

[(σ

− σ

)

+ 4σ

]

1/2

√

= σ

.So

the invariants we ﬁrst identiﬁed in Equations (9.5) in two dimensions are

functions of I

and J

The right-hand side of Equation (9.14) turns out to be the maximum

shear stress in plane strain. You can show this by setting the derivative

of Equation (9.2) equal to 0. If the axes were, in addition, chosen to be

parallel to the principal stresses, σ

would vanish, leaving:

=±

(σ

− σ

)

The directions of the maximum shear stresses would then be 45

◦

and

135

◦

to the principal axes. (To show this, determine the orientation of

the planes on which σ

is a maximum, using a procedure similar to that

which we used to obtain Equations (9.3), and compare these planes with

the orientations of the planes on which σ

is a maximum.)

Momentum balance

The stress equilibrium equations are derived by balancing forces in the

directions of the coordinate axes. Consider forces in the x-direction on

ablock of size dx dy dz as shown in Figure 9.5:



=−σ

dy dz+



∂σ

∂x



dy dz −σ

dx dz+



∂σ

∂y



dx dz

−σ

dx dy +



∂σ

∂z



dx dy + ρg

dx dy dz = 0

The ﬁrst two terms on the right are the normal forces on the faces of

the block that are normal to the x-axis. Note that in each case, the stress

(shown in Figure 9.5)ismultiplied by the area of the face, in this case

262 Stress and deformation

dy dz,toobtain a force. The next four terms are the shear forces in the

x-direction on faces normal to the y- and z-axes, respectively. The last

term is the body force; g

in this term represents the component of the

gravitational acceleration that is parallel to the x-axis. Canceling like

terms of opposite sign and dividing by dx dy dz yields:

∂σ

∂x

∂σ

∂y

∂σ

∂z

+ ρg

= 0

Similar expressions are readily obtained in the y- and z-directions. Using

the summation convention, these become:

∂σ

∂x

+ ρg

= 0 (9.15)

As i is repeated in the ﬁrst term, this represents three terms. However,

j is not repeated, so we can write separate equations for j = x, y, and z.

Thus Equation (9.15) represents three equations.

Because F = ma = m(dv/dt) = (d/dt)(mv)where m is mass, a

is acceleration, v is velocity, and mv is momentum, Equations (9.15)

represent conservation (e.g. d/dt = 0) of linear momentum.

Deformation

Having applied a stress to a medium, we expect strain or deformation to

occur. Suppose

x, y, and z (Figure 9.6) represent the displacement of a

particle from P to P



in the directions of the coordinate axes, respectively.

We will consider inﬁnitesimal displacements so the time required for the

deformation → 0.

Figure 9.6. Components

of a displacement from P to



Normal strain in the x-direction at P is deﬁned as:

= Lim

→0





(9.16)

where  is the length of a line drawn in the x-direction, and  is the

elongation of that line, so / is the elongation of the line per unit

length. Referring to Figure 9.7,ifaline, initially of length ,istranslated

such that its left end moves a distance

x in the x-direction, its right end

moves a distance

x + (∂x/∂ x)inthis direction, and the x-component of

its new length is  + , then substituting into Equation (9.16) yields:

= Lim

→0

x +(∂x/∂ x) − x



∂

∂x

(9.17)

By taking the limit as →0weeliminate the variation with x, thus obtain-

ing ε

at point P. Similarly: ε

= ∂y/∂ y and ε

= ∂z/∂z.



+ ∆

x + 

∂

∂ x

Figure 9.7. Elongation of

a line during deformation.

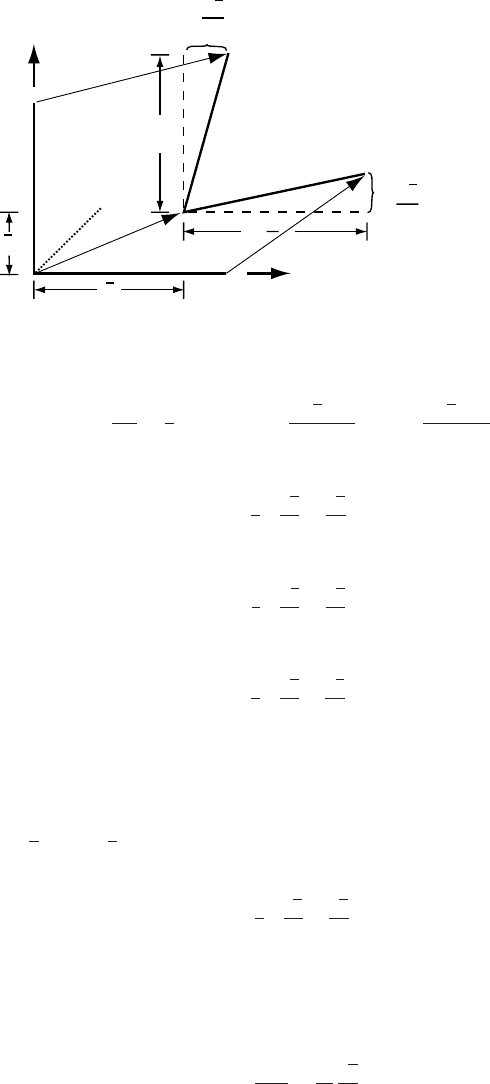
Deformation 263



∂

∂ y



∂

∂ x

Figure 9.8. Change in a

right angle during

deformation.

Shear strain is deﬁned as one half the decrease in an initially right

angle. Referring to Figure 9.8, this can be expressed as:

θ

Lim

→0



tan

−1

(∂x/∂ y)



+ tan

−1

(∂y/∂ x)





For inﬁnitesimal changes, θ ≈ tan θ so:



∂

∂y

∂

∂x



(9.18a)

and similarly



∂

∂y

∂

∂z



(9.18b)

and



∂

∂z

∂

∂x



(9.18c)

As before (Chapter 2), there are nine components of strain. Thus, this

is another second rank tensor, the strain tensor. It, too, is symmetric

because ε

= ε

and so forth.

In general, shear results in rotation as well as distortion. For example,

if ∂

x/∂y = ∂y/∂x in Figure 9.8, the dotted line inclined at 45

◦

to the

x-axis will be rotated through an angle:



∂

∂y

−

∂

∂x



Similar expressions may be written for other rotations.

To obtain rates, which are normally of greater interest in a deforming

ice mass, we differentiate with respect to time. Thus, the normal strain

rate in the x-direction, ˙ε

, is:

˙ε

dε

∂

∂x

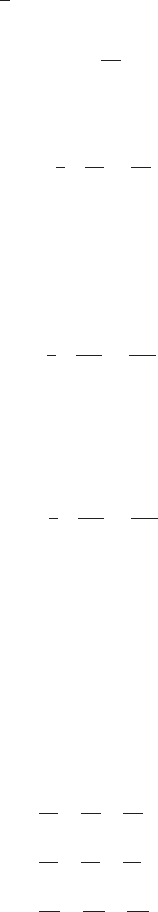
264 Stress and deformation

Velocity is deﬁned as a change in distance with time, or if u is the velocity

in the x-direction, u = d

x/dt. Thus, we obtain:

˙ε

∂u

∂x

(9.19)

Similarly, shear strain rates become:

˙ε



∂u

∂y

∂v

∂x



(9.20)

and so forth.

The symmetry of Equation (9.20) suggests the possibility of again

using the summation convention to write expressions for the strain rates,

thus:

˙ε



∂u

∂x

∂u

∂x



(9.21)

If i =j in this expression, it reduces to Equation (9.19), so this formulation

represents both shear and normal strain rates.

Similarly, the rotation rate tensor is:

˙ω



∂u

∂x

−

∂u

∂x



(9.22)

The rotation rate tensor is antisymmetric because ˙ω

=−˙ω

. Note also

that ˙ω

= 0when i = j.Inother words, pure stretching does not result in

rotation. If ˙ω

= 0 for all i, j the ﬂow is said to be irrotational. Rotations

do not change the size or shape of an element, so they do not require the

application of a stress.

As implied by the notation ∂u

/∂x

(i, j =x, y, z), the velocity vector

has three components, and each of them can vary in each of the three

coordinate directions. Thus there are nine velocity derivatives.

∂u

∂x

∂u

∂y

∂u

∂z

∂v

∂x

∂v

∂y

∂v

∂z

∂w

∂x

∂w

∂y

∂w

∂z

This is sometimes called the velocity derivative tensor. The velocity

derivative tensor is not symmetric, as ∂u

/∂x

= ∂u

/∂x

in general.

Therefore, it can be decomposed into symmetric and antisymmetric

parts. The symmetric part is represented by Equation (9.21), and the

anti-symmetric part by Equation (9.22).

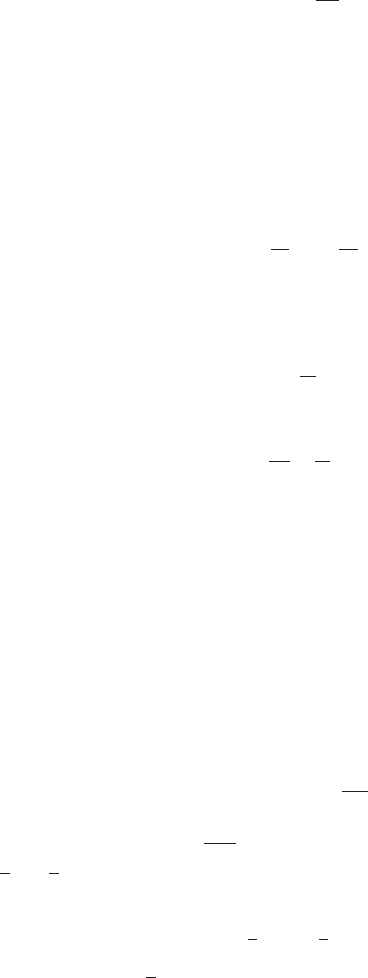
Deformation 265

Logarithmic strain

In Equation (9.16)wedeﬁned strain by:

ε = Lim

→0





where  is the initial length of a line and  is the elongation of that line.

This deﬁnition is suitable for small (inﬁnitesimal) strains. However, when

calculating strains or strain rates from measurements, the total strain is

normally not inﬁnitesimal. This is, in part, because deformations must

be large enough to exceed the uncertainty in the measurement method.

If strains are inﬁnitesimal, we can replace  with d. The total

strain is then the sum of the inﬁnitesimal strains, or:

ε =

=



=

d







d



where 

is the initial length of the line and 

is its ﬁnal length. Integrating

yields:

ε = ln



(9.23)

or in terms of rates:

˙ε =

t



(9.24)

where t is the time interval between measurements. This is known as

logarithmic strain.

General equations for transformation of strain

in two dimensions

Our next objective is to develop an expression for the strain rate in an

arbitrary direction, θ .Tosimplify the equations, we restrict the analysis to

the case of plane strain. We will then take the derivative of this expression

and set it equal to zero to ﬁnd the directions in which ˙ε(θ)ismaximum

and minimum (the principal strain rates). Finally we will look at the

implications of this in terms of the ﬂow law.

Let us examine the elongation of line

OP in Figure 9.9a. The line

has an initial length  and makes an angle θ with the x-axis. The line is

stretched to a ﬁnal length



through a displacement with components

x and y in the x- and y-directions, respectively. The elongation is given

by (Figure 9.9a):

 = x cos θ + y sin θ (9.25)

The displacement x is a consequence of strain parallel to the x-axis and

a shear strain which results in tilting of any line that is initially normal

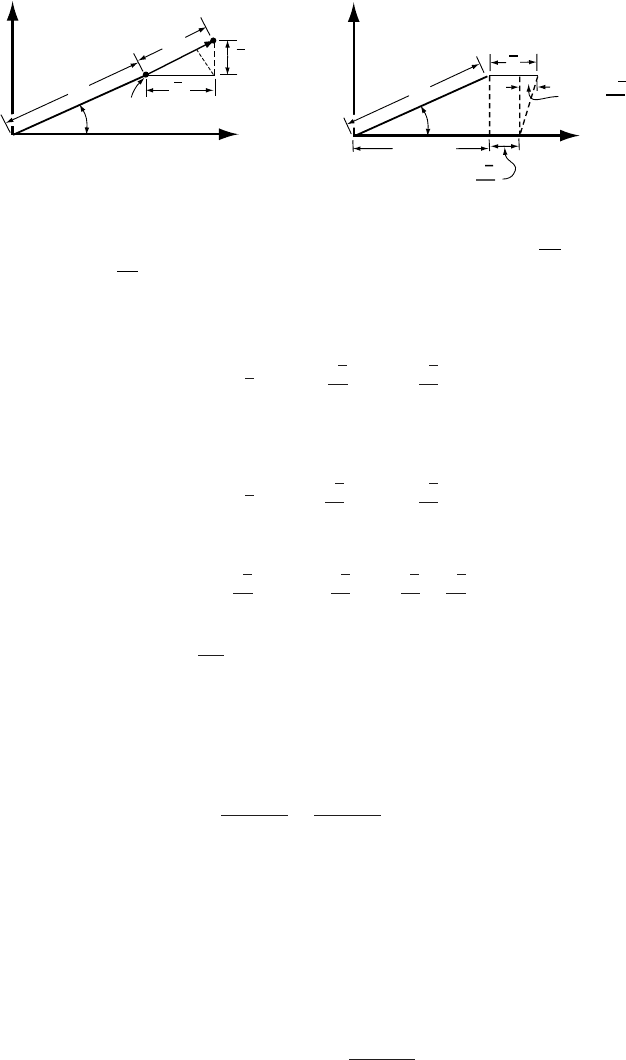
266 Stress and deformation



∆



sin

 cos q

∂

∂ x



sin

∂

(a) (b)

Figure 9.9. (a) Components of strain of a line of initial length  = OP and ﬁnal

length 

OP, and (b) details of the shear component of the strain.

to the x-axis (Figure 9.9b), thus:

x =  cos θ

∂

∂x

+  sin θ

∂

∂y

(9.26a)

The origin of the two terms on the right-hand side may be clariﬁed by

reference to Figures 9.7 and 9.8, respectively. Similarly:

y =  sin θ

∂

∂y

+  cos θ

∂

∂x

(9.26b)

Substituting Equations (9.26) into Equation (9.25) yields:

 =  cos

∂

∂x

+  sin

∂

∂y

+ 



∂

∂y

∂

∂x



cos θ sin θ

Finally, dividing by ; noting that Lim

→0

(/) =ε(θ ), the strain along

the length of line

OP; and using Equations (9.17) and (9.18a)toexpress

the derivatives in terms of strains yields:

ε(θ) = ε

cos

θ + ε

sin

θ + 2ε

cos θ sin θ

With the trigonometric identities used earlier (p. 254), this becomes:

ε(θ) =

+ ε

− ε

cos 2θ + ε

sin 2θ (9.27)

Strain rates can be obtained by taking the derivative with respect to time.

Equation (9.27)isauseful relation for obtaining normal strains or strain

rates in an arbitrary direction, θ,when values in the coordinate directions

x, y are known.

To obtain the maximum and minimum values of ε(θ ), the principal

strain rates, we proceed as before (Equations (9.3)) to take the derivative

with respect to θ, set it to zero, and solve for θ, thus:

tan 2θ

2˙ε

˙ε

− ˙ε

(9.28)

Condition that principal axes coinside 267

The two solutions for θ are the directions in which the strain rate is a

maximum and minimum. The magnitudes of the principal strain rates

can be obtained as we did for the principal stresses (Equation (9.4)).

Condition that principal axes of stress and strain

rate coincide

In calculating the stress and velocity ﬁelds in a glacier in Chapter 10,

we will need to assume that the principal axes of stress and strain rate

coincide. Let us explore the consequences of this condition.

We found earlier (Equation (9.3b)) that the angle which the principal

stresses make with the x-coordinate may be obtained from:

tan 2θ

stress

2σ

− σ

2σ



− σ



Note that it does not matter whether we use deviatoric or total stresses

here, as σ



= σ

and σ



− σ



= σ

− P − (σ

− P) = σ

− σ

The condition that the principal axes of stress and strain rate coincide

is θ

stress

= θ

,oratany given point in the medium:

2σ



− σ



2˙ε

˙ε

− ˙ε

The only way to satisfy this condition in the general case is to let:

˙ε

= λσ



;˙ε

= λσ



;˙ε

= λσ



where λ is a scalar; that is, its value at the particular point in the medium

is independent of the direction in which the stress is acting. However, λ

may vary from one point to another in the medium, so λ = λ(x, y, z).

The fact that λ is a scalar implies that the deforming material is

isotropic and incompressible. Thus, under a given stress, it will deform

at the same rate regardless of the direction in which the stress is applied.

Obviously, this is an approximation in a material such as ice that ﬁrst has

an hexagonal crystal structure, and secondly can develop a fabric with a

preferred orientation. [If the material were compressible, a compressive

deviatoric stress in, say, the x-direction, σ



,would cause more defor-

mation than the corresponding tensile deviatoric stress in the y-direction

(which must equal σ



in magnitude in plane strain). Thus, λ would differ

between the two directions.]

We generalize this assumption to three dimensions and formalize it

by writing:

˙ε

= λσ



(9.29)

268 Stress and deformation

remembering that

˙ε



∂u

∂x

∂u

∂x



(9.30)

and



= σ

−



Because the stress and strain rate in the ﬂow law are deﬁned in terms

of either the effective or the octahedral stress and strain rate, we can write

out the ﬁrst few terms of the effective strain rate and substitute Equation

(9.29) into the right-hand side, as follows:

˙ε



˙ε

+ ˙ε

+ ···





2

+ λ

2

+ λ

2

+ ···





2

+ σ

2

+ σ

2

+ ···



= λ

Dropping the subscript e for convenience (and also because the ﬂow law

can be written in terms of either the effective or the octahedral stress and

strain rate), we obtain:

˙ε = λσ = f (σ )soλ =

f (σ )

(9.31)

Here, f (σ )isused to emphasize that in the general case, λ is a function

of the applied stress.

Afew examples will serve to illustrate the meaning of λ.

Newtonian ﬂuid: λ = 1/η,where η is the Newtonian viscosity so in

this case λ is not a function of σ (see Equation (2.17)).

Power-law ﬂuid: λ = σ

n−1

,so˙ε = λσ =

(

σ/B

)

Perfectly plastic material: as noted earlier (Figure 9.4), in a per-

fectly plastic material there is no deformation below a critical stress,

σ = k,soλ = 0 for σ<k. When σ = k, the material deforms at a rate

such that the stress does not exceed k.Inother words, λ depends on

˙ε : λ = f

(˙ε).

In the case of the power-law ﬂuid, λ varies with σ and B, and because

B is a function of temperature, density, crystal size and orientation, and

perhaps other factors, λ varies with these properties as well.

Combining Equations (9.29), (9.30), and (9.31), writing ˙ε in terms

of velocity derivatives, and using the summation convention, we now

Summary 269

have the following relation between individual components of the stress

and strain rate tensors:



∂u

∂x

∂u

∂x



f (σ )



(9.32a)

This represents nine equations, only six of which are independent.

Together with Equation (9.15):

∂σ

∂x

+ ρg

= 0 (9.32b)

which represents an additional three equations, we have nine independent

equations which can be solved for the three normal stresses, three shear

stresses, and three velocities. Our objective in Chapter 10 will be to do

this, but to simplify the problem, we will conﬁne our attention to plane

strain.

Summary

In this chapter, we have reviewed some elementary principles of con-

tinuum mechanics with a particular focus on those principles needed

to understand much of the classical as well as the modern literature on

glacier ﬂow.

In the ﬁrst part of the chapter, we deﬁned stress and showed that if

we know the stresses in one coordinate system, we can calculate them

in another system rotated with respect to the ﬁrst. This allowed us to

calculate the direction and magnitude of the maximum and minimum

normal stresses, the principal stresses.Wedid the calculation in two

dimensions, but the extension to three dimensions is straightforward,

though tedious. We found that shear stresses vanish in coordinate systems

chosen with axes aligned parallel to the principal stresses.

The orientation and magnitude of the principal stresses is a property

of the stress ﬁeld and not of the orientation of the axes. Thus, there

are certain combinations of the stresses that must be independent of the

orientation of the axes: the invariants of the stress tensor. Glen’s ﬂow

law for ice is based on the second of these invariants. This is logical

because it is invariant, and also because the von Mises yield criterion

can be expressed in terms of this invariant. Recent experimental data

have validated this approach.

In the second part of the chapter, we derived the stress equilibrium

or momentum balance equations.

In the third part, we deﬁned strain and derived equations for calcu-

lating strains or strain rates in coordinate systems rotated with respect

to one another. These equations are similar to those for transformation

270 Stress and deformation

of stress. As with stresses, we introduced the concept of principal strain

rates.

Finally, we showed that if a material is isotropic and incompressible,

the principal axes of stress and strain rate coincide. Ice is clearly not

isotropic and incompressible, but this approximation has proven to be a

convenient starting point for calculations of glacier ﬂow.