Hirsch M.J., Pardalos P.M., Murphey R. Dynamics of Information Systems: Theory and Applications

Подождите немного. Документ загружается.

326 N.R. Gans and J.W. Curtis

ˆx

= AKy

+A(A −KHA)Ky



−HAKy

−HA(A−KHA)Ky



= Ky

+(A −KHA)Ky

+(A −KH A)(A −KHA)Ky

(17.6)

ˆx



i=0

(A −KHA)

k−i

(17.7)

This derivation provides a method to approximate a KF given a batch or list of

measurements from a single known sensor. First, precompute the Kalman gain K

and the discount matrix A − KHA. Then sum the individual contributions from

each measurement as expressed in (17.7) to obtain a ﬁnal estimate. If our initial

information was such that the ﬁlter began in steady state, then this would yield an

optimal estimate in the sense that the estimate x

exactly equals the output from

running a KF from time 0 up to k.

If there is insufﬁcient a priori information to begin the estimation ﬁlter in steady

state, the estimate produced by this technique would be suboptimal. This problem

can be by addressed by simply assuming that the ﬁlter achieves steady-state oper-

ation after s time-steps (an assumption that is true in practice whenever the sys-

tem is observable, stabilizable, and well modeled). This would imply that the mea-

surements made on or after time s could be used in the ﬁnal estimate as speciﬁed

in (17.7). However, the ﬁrst s terms would be wrong; alternatively we could re-

deﬁne time-step s as the temporal origin and redeﬁne all subsequent time-steps as



=k +s.

17.2.2 Moving Average Implementation

Assume again that we have augmented the measurement list Y such that it contains

a pseudo-measurement at time 0, which guarantees an optimal ﬁlter would operate

in steady state for all time. Then, from (17.7), the optimal estimation of x

is given

ˆx



i=0

(A −KHA)

k−i

(17.8)

17 A Moving Horizon Estimator Performance Bound 327

Now suppose that we wish to implement a truncated summation (moving aver-

age) of the measurements as

ˆx



i=k−N

(A −KHA)

k−i

+Φ(k −N) (17.9)

where N is the length of the moving horizon and Φ(k − N) is the sum of the ne-

glected terms. Deﬁne a new estimator given by

ˆx





i=k−N

(A −KHA)

k−i

(17.10)

Clearly, the error between this estimate and the KH estimate will be



ˆx

−ˆx



Φ(k −N)



17.3 MHE Performance Bound

The aim of this paper is to characterize the size of Φ(k −N), i.e., derive a bound on

Φ(k −N) as a function of N . Note that e

does not refer to the true estimate

error ˆx

−x

, which is generally unknown.

The eigenvalues of the matrix A −KHA will lie inside the unit circle, since we

have assumed a steady-state KF. When the eigenvalues of A − KHA have mag-

nitude less than one, (17.10) represents a convergent geometric series with a ﬁnite

sum.

Write the error e



ˆx

−ˆx





i=0

(A −KHA)

t−i

−



i=t−N

(A −KHA)

t−i



t−N



i=0

(A −KHA)

t−i



≤

t−N



i=0



(A −KHA)

t−i



≤

t−N



i=0



(A −KHA)



t−i

Ky



328 N.R. Gans and J.W. Curtis

Let ¯y be the largest expected value of Ky

 (or the norm of known sensor satura-

tion) on the interval i ∈[0,t −N ]. Then we have that

≤¯y

t−N



i=0



(A −KHA)



t−i

(17.11)

If A −KHA< 1, the sum in (17.11) converges as follows (where F



=A −

KHA)

S =F

N+1

+···+F

FS =F

N+1

+···+F

t+1

S −FS =F

−F

t+1

(1 −F)S =



−F

t+1



S =

−F

t+1

1 −F

S =

A −KHA

−A −KHA

t+1

1 −A −KHA

The bound on e

can then be characterized as

≤¯y

A −KHA

−A −KHA

t+1

1 −A −KHA

≤C



A −KHA

−A −KHA

t+1



where C



¯y

1−A−KHA

.Ast +1 −N>0 implies A −KHA

t+1−N

< 1, it can

be seen that

≤C

A −KHA



1 −A −KHA

t+1−N



≤C

A −KHA

This allows the derivation of an explicit algorithm for choosing a horizon length,

given some maximum desired error level e

lne

≤lnC

+N ln A −KHA (17.12)

so choose a horizon length N such that

N ≥

ln e

−lnC

lnA −KHA

Note that in (17.12) the horizon length might be negative if the error is chosen

too large. This situation implies that using a zero-length horizon would satisfy the

17 A Moving Horizon Estimator Performance Bound 329

performance requirement. Note also that N grows to inﬁnity as e

goes to zero

(because the denominator in (17.12) is always negative).

17.3.1 Situation When A −KHA≥1

Having all eigenvalues of A − KHA less than one does not guarantee that A −

KHA< 1. In this case, the matrix series in (17.10) will converge, but the series in

(17.11) will not. This can be detected easily by testing whether the A−KHA≥1.

If so, the bound calculation can be amended to address this issue.

Test (A −KHA)

 for increasing values of p until (A −KHA)

< 1. Take

¯y

1−(A−KHA)



and

≤C



(A −KHA)



The conditions under which the eigenvalues of A −KHA are in the unit circle but

A −KHA > 1 are not clear at this time, though it appears to depend on A and

R. This is an avenue of open investigation and future work.

17.3.2 Alternative Derivation

The bound developed in Sect. 17.3 is overly conservative, sometimes larger than the

true error by several orders of magnitude. A similar approach can produce a tighter

bound at the expense of greater computation time. However, given reasonable length

horizon and dimension of state, the additional computation time is negligible.

Again take the error e



ˆx

−ˆx



t−N



i=0

(A −KHA)

t−i



and set F =(A −KHA). Then we have



t−N

N+1

t−N −2

+···+F



There must exist a vector ¯y such that



¯y +F

N+1

¯y +···+F

¯y





N+1

+···+F



¯y



t−N

N+1

t−N −2

+···+F



(17.13)

330 N.R. Gans and J.W. Curtis

We take advantage of two properties. First, given the singular value decompo-

sition of a matrix F = UV, the vector of V corresponding to the largest singu-

lar value will give max Fv. Second, given the svd’s of matrices F, F

,...,F

as the power increases, the V matrices quickly converge to a constant, i.e., given

= U



and F

i+1

= U

i+1



i+1

, then V

≈ V

i+1

for a appropriately

large i. In practice, V

and V

i+1

are the same to within i decimal places. There-

fore, for sufﬁciently large N, ¯y will point along a direction close to the vector of V

corresponding to the largest singular value, and ¯y can be chosen appropriately,

such as the maximum expected value or known saturation of the sensors. Then





N+1

+···+F



¯y



≤





I +F +···+F

k−N





¯y

≤





k−N+1



(F +I)

−1



¯y

≤





k+1



(F +I)

−1



¯y

It may be undesirable to have k explicitly in the expression for e

, since it will

then have to be recomputed for each time. Under the assumption that F

≤F

N+1

(in the sense that F

x≤F

N+1

x for any vector x), e

can be upper bounded

≤¯y



(F +I)

−1



17.4 Simulation and Analysis

Simulations and Monte Carlo analysis have been conducted to conﬁrm the accuracy

of the bound.

17.4.1 Simulation of Moving Horizon Estimator and Error Bound

First, an illustrative test of the Moving-horizon estimator is preformed, and its per-

formance is compared to the maximum error e

bound. A two-dimensional linear

time-invariant system of the form (17.1) is simulated with

A =



1 .1



,H=





Q =0.75



0.033 0.05

0.05 1



,R=0.3



10.3

0.31



This represents 2nd order random walk process with sampling time 0.1 sec, full state

feedback, and correlated sensor noise. For the moving-horizon estimator, a horizon

length of 5 time-steps was used.

17 A Moving Horizon Estimator Performance Bound 331

Fig. 17.1 Simulation of KF and MHKF estimators

Fig. 17.2 The norm of estimation errors and the estimated bound

Figure 17.1 shows the system state simulated for 20 seconds (200 time samples)

and the state estimates from both the Kalman ﬁlter and the moving horizon estima-

332 N.R. Gans and J.W. Curtis

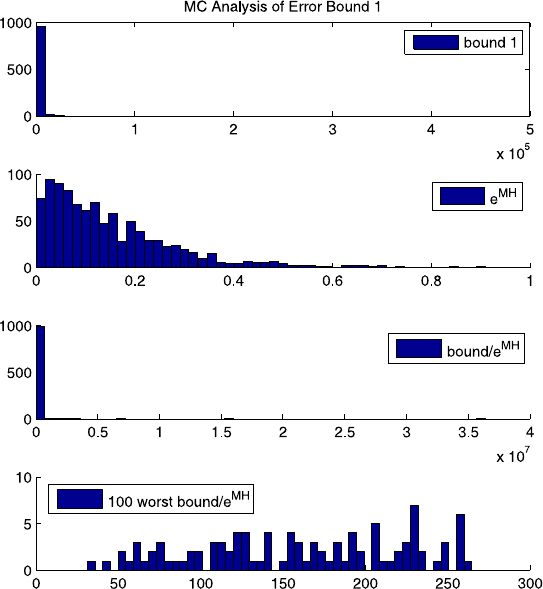
Fig. 17.3 Monte Carlo analysis of Bound 1

tor. Both the Kalman ﬁlter and the moving-horizon estimator track the true signal

well.

The bound on e

for this system using the method in Sect. 17.3.1 is

≤8.96. The bound using the method in Sect. 17.3.2 is e

≤ 0.92. This is

illustrated in Fig. 17.2. A semi-log plot is used since the errors are rather small.

Both bound estimates are met, and as expected, the second method of calculating

the bound produces a lower bound.

17.4.2 Monte Carlo Analysis of Error Bound

The performance for a common system was demonstrated in Sect. 17.4.1. However,

we wish to evaluate the performance for a wide variety of systems. To this end, a

Monte Carlo analysis was performed with a large number of random systems.

One thousand (1000) random systems are generated as follows. First, generate

four random matrices Z

∈ R

2×2

, i ∈{1 ...4} where each element is a zero-mean

17 A Moving Horizon Estimator Performance Bound 333

Fig. 17.4 Monte Carlo analysis of Bound 2

Gaussian random variable with unit variance. If the condition number of Z

> 10,

recalculate Z

until a suitable matrix is found. Take initial system matrices



1 .1









.1 .01

.01 .1





.1 .01

.01 .1



and create random matrices

A =Z

−1

,H=Z

−1



−1



−1

To ensure that the covariance matrices are positive-semideﬁnite and symmetric, the

ﬁnal values of Q and R are generated as

Q =





T



,R=





T



334 N.R. Gans and J.W. Curtis

where (·)

represent the matrix square root.

Each of the 1000 random systems are tested for both the Kalman ﬁlter and

moving-horizon estimators. Histograms are generated of the results in Figs. 17.3

and 17.4. It can be seen that both bounds have some outliers that are very large,

though the second method of producing a bound is typically smaller. To best illus-

trate the tightness of the bound, we consider the ratio

bound

. Any ratio less than one

indicates the bound was violated. Motivated by robust control applications, where

min/max performance is critical, we focus on the 100 smallest values of this ratio

from the distribution, representing the cases where the bound was closest to the true

value of e

. It is seen that both bounds are never violated by e

, and the second

bound is roughly an order of magnitude tighter, even for the minimum ratios.

17.5 Future Work

There are several avenues of future work. The bounds in this paper represent useful

measures to ensure robust performance, but for many cases the bounds are typically

much larger than the true errors, so some method to get a tighter, more accurate

bound is desirable. Another approach is to generate a stochastic bound, that is a

tighter bound with a known probability that the bound is not exceeded. Experiments

will also be performed to test the bound in real scenarios when the system is not

perfectly modeled.

References

1. Alessandri, A., Baglietto, M., Battistelli, G.: Receding-horizon estimation for discrete-time

linear systems. IEEE Trans. Autom. Control 48(3), 473–478 (2003)

2. Brown, R.G., Hwang, P.Y.C.: Introduction to Random Signals and Applied Kalman Filtering

with Matlab Exercises and Solutions, 3rd edn. Wiley, New York (1996)

3. Jazwinski, A.: Limited memory optimal ﬁltering. IEEE Trans. Autom. Control 13(5), 558–563

(1968)

4. Kwon, W.H., Kim, P.S., Park, P.G.: A receding horizon Kalman ﬁr ﬁlter for discrete time-

invariant systems. IEEE Trans. Autom. Control 44(9), 1787–1791 (1999)

5. Ling, K.V., Lim, K.W.: Receding horizon recursive state estimation. IEEE Trans. Autom. Con-

trol 44(9), 1750–1753 (1999)

6. Plett, G.L., Zarzhitsky, D., Pack, D.: Out of order sigma point Kalman ﬁltering for target

localization using cooperating unmanned aerial vehicles. In: Advances in Cooperative Control

and Optimization, pp. 21–43 (2007)

7. Rao, C.V., Rawlings, J.B., Lee, J.H.: Constrained linear state estimation–a moving horizon

approach. Automatica 37(10), 1619–1628 (2001)

8. Wang, Z.-O., Zhang, J.: A Kalman ﬁlter algorithm using a moving window with applications.

Int. J. Syst. Sci. 26(8), 1465–1478 (1995)

Chapter 18

A p-norm Discrimination Model for Two

Linearly Inseparable Sets

Pavlo Krokhmal, Robert Murphey,

Panos M. Pardalos, and Zhaohan Yu

Summary We propose a new p-norm linear discrimination model that generalizes

the model of Bennett and Mangasarian (Optim. Methods Softw. 1:23–34, 1992)

and reduces to linear programming problems with p-order conic constraints. We

demonstrate that the developed model possesses excellent methodological and com-

putational properties (e.g., it does not allow for a null separating hyperplane when

the sets are linearly separable, etc.). The presented approach for handling linear pro-

gramming problems with p-order conic constraints relies on construction of poly-

hedral approximations for p-order cones. A case study on several popular data sets

that illustrates the advantages of the developed model is conducted.

18.1 Introduction

Consider two discrete sets A, B ∈ R

comprised of k and m points, respectively:

A ={a

,...,a

}, B ={b

,...,b

}. One of the principal tasks arising in machine

learning and data mining is that of discrimination of these sets, namely, constructing

a surface f(x) =0 such that f(x)<0 for any x ∈A and f(x)>0 for all x ∈B.

P. Krokhmal (



) · Z. Yu

Department of Mechanical and Industrial Engineering, University of Iowa, Iowa City, IA 52242,

USA

e-mail: krokhmal@engineering.uiowa.edu

Z. Yu

e-mail: zhaohan-yu@uiowa.edu

R. Murphey

Air Force Research Lab, Eglin AFB, FL, USA

e-mail: robert.murphey@eglin.af.mil

P.M. Pardalos

Department of Industrial and Systems Engineering, University of Florida, Gainesville, FL 32611,

USA

e-mail: pardalos@uﬂ.edu

M.J. Hirsch et al. (eds.), Dynamics of Information Systems,

Springer Optimization and Its Applications 40, DOI 10.1007/978-1-4419-5689-7_18,

335