Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 29

1.7.2 Hydrogen Diﬀusion

Hydrogen in metals provides itself an important and fascinating topic of ma-

terials science. It has also attracted considerable interest from the viewpoint

of applications. For example, the idea of hydrogen storage in metals is based

on the high solubility and fast diﬀusion of hydrogen in some metal-hydrogen

systems. Permeation of hydrogen through palladium membranes for hydro-

gen puriﬁcation is an old and well-known application based on the very fast

diﬀusion. Nowadays, diﬀusion of hydrogen plays a key role for fuel cells which

use hydrogen or hydrocarbons as fuels.

Hydrogen forms interstitial solid solutions with most metallic elements.

Some metals have a negative enthalpy of solution and a high solubility for

hydrogen (e.g. group IV transition metals, group V transitions metals, and

palladium) and form hydrides at higher hydrogen concentrations. Other met-

als have a positive enthalpy of solution and a relatively low solubility (e.g.

group VI metals, group VII metals, and iron).

From a scientiﬁc point of view diﬀusion of hydrogen is signiﬁcantly dif-

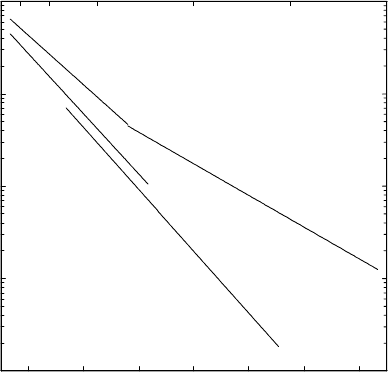
ferent from diﬀusion of other interstitial solutes. Fig. 1.14 shows an Arrhe-

nius plot for diﬀusion of hydrogen and its isotopes deuterium and tritium in

the bcc transition metal niobium (for references see Chap. 9 in [6]). We use

Fig. 1.14 to illustrate some characteristic features of hydrogen diﬀusion:

-12

-11

-10

-9

-8

3 4 5 6 7 8

500 400 300

200 150

-1

/ 10

-3

-1

D / m

-1

T / K

Fig. 1.14. Diﬀusion of the hydrogen isotopes H, D, and T in niobium.

30 Helmut Mehrer

– Diﬀusion of hydrogen and its isotopes is extremely rapid: Diﬀusivities

exceed that of heavier interstitials by many orders of magnitude as can

be seen from a comparison of Figs. 1.13 and 1.14. From Fig. 1.14 we get

=8× 10

−9

−1

near 300

C. According to (1.36) the reciprocal

mean residence time τ

−1

of H atoms is about 10

−1

.Thisextremely

high value is of the order of the Debye frequency of niobium.

– Hydrogen has three isotopes (H, D, T): These isotopes diﬀer consider-

ably in their isotopic masses, which oﬀers the possibility to study large

isotope eﬀects. Fig. 1.14 shows that normal hydrogen (H) diﬀuses more

rapidly than deuterium (D), and deuterium diﬀuses more rapidly than

tritium (T). In addition the activation enthalpies of hydrogen isotopes

are diﬀerent and obey the inequalities

∆H

<∆H

. (1.53)

In the classical regime the activation enthalpy of a diﬀuser is exclusively

determined by the chemistry of the system and not by the isotopic mass.

The latter enters the diﬀusion coeﬃcient only via the mass dependence of

the attempt frequency. If many-body and quantum eﬀects are negligible

the attempt frequency ν

is related to the mass m of the diﬀuser simply

∝

√

. (1.54)

This shows that (1.53) represents a non-classical eﬀect. Similar non-

classical eﬀects have been observed for hydrogen diﬀusion in the metals

vanadium and tantalum.

– Hydrogen is the lightest atom. As a consequence, quantum eﬀects in dif-

fusion can be observed which are hardly detectable for heavier diﬀusers.

The deviation of hydrogen diﬀusivity from an Arrhenius law below room

temperature (see Fig. 1.14) has been attributed to incoherent tunneling

(e.g. [33]).

– Positive muons can be considered in several respects as light isotopes of

hydrogen [43]. The muon mass is by a factor of nine smaller than the

proton mass. Like the hydrogen nuclei, the muons may be considered as

very heavy compared with the electrons but nevertheless light compared

with most metal atoms. A prefered topic studied with positive muons in

metals is quantum diﬀusion (see, e. g., [44]).

The very fast diﬀusion and the often high solubility of hydrogen have con-

sequences for the experimental techniques used in hydrogen diﬀusion stud-

ies. Concentration-proﬁle methods, permeation methods based on Fick’s ﬁrst

law, absorption and desorption methods, electrochemical methods, and re-

laxation methods (Gorsky eﬀect, magnetic after eﬀect, etc.) are in use. Due

to the favourable gyromagnetic ratio of the proton and due its large incoher-

ent scattering cross section for neutrons, NMR and QENS, respectively, (see

1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 31

Chaps. 2 and 3 and [33]) are well suited for hydrogen diﬀusion studies. For a

more thorough discussion of hydrogen diﬀusion the reader is referred to text-

books [2,3], to reviews [30,32] and to Chap. 9 of the data collection [6]. Muon

diﬀusion can be studied by the muon spin resonance (µSR) technique [45],

which has some similarities with β-NMR (see Chap. 9).

1.8 Self-Diﬀusion in Metals

Self-diﬀusion is most conveniently studied by the tracer method described in

Sect. 1.4. As an example D values from

Ni tracer measurements in nickel are

displayed in Fig. 1.15 according to [46, 47]. An enormous diﬀusivity range of

about 9 orders of magnitude has been covered by the combination of mechan-

ical sectioning [46] and sputter sectioning [47]. Most of the more important

metallic elements have been studied by tracer methods over similarly wide

ranges. In some cases the tracer data have been supplemented by additional

techniques. For example, NMR proved to be very useful in the cases of alu-

minium and lithium (cf. Chap. 9) where no radioisotopes appropriate for

tracer diﬀusion studies are available. For a collection of data and information

about the method(s) used for each metal the reader is referred to Chap. 2

in [6].

-22

-21

-20

-19

-18

-17

-16

-15

-14

-13

-12

5 6 7 8

9 10

11 12 13

1600 1200 1000 800

grinding

sputtering

-1

/ 10

-4

-1

D / m

-1

T / K

Fig. 1.15. Self-diﬀusion of

Ni in nickel. Open circles: data from mechanical sec-

tioning; full circles: data from sputter sectioning.

32 Helmut Mehrer

The dominating mechanism of self-diﬀusion

in metallic elements is the

vacancy mechanism illustrated in Fig. 1.9. Using (1.37) and (1.43) the diﬀu-

sion coeﬃcient of tracer atoms can be written as

D = fa

ωC

= fa

exp



+ S



exp



−

+ H



. (1.55)

The Arrhenius parameters of (1.20) have the following meaning for vacancy

mediated self-diﬀusion:

∆H = H

+ H

(1.56)

and

= fa

exp



+ S



. (1.57)

As already mentioned in Sect. 1.6 the correlation factor accounts for the

fact that for vacancy-mediated diﬀusion the tracer atom experiences some

‘backward correlation’ whereas the vacancy itself performs a random walk.

For monovacancies in cubic lattices f is a temperature-independent quantity,

which is approximately given by

f ≈ 1 −

(1.58)

where Z is the coordination number. Vacancy jumps into one of the Z di-

rections occur with the probability 1/Z and an immediate backward jump

eﬀectively ‘cancels’ two tracer jumps. (1.58) is a ‘rule of thumb’. Exact values

according to [2] are listed in Table 1.2.

Table 1.2. Correlation factors of vacancy-mediated self-diﬀusion in cubic lattices.

Structure fcc bcc sc diamond

f 0.7815 0.727 0.653 0.5

For self-diﬀusion in non-cubic crystals correlation factors are orientation

and temperature dependent. For example, the two correlation factors in hcp

crystals depend on the ratio of the jump rates within and oblique to the basal

plane (see, e.g., [2]).

1.8.1 Face-Centered Cubic Metals

Self-diﬀusion coeﬃcients of several face-centered cubic (fcc) metals are shown

in the Arrhenius diagram of Fig. 1.16. For each metal the temperature scale is

For fcc metals at temperatures above about 2/3 of the melting temperature an

additional contribution of divacancies (see Fig. 1.10) has been proposed (see [22]

and the textbooks [2, 3]), which for reasons of simplicity will be not considered

here.

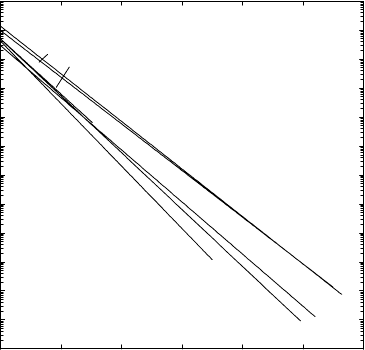
1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 33

-23

-22

-21

-20

-19

-18

-17

-16

-15

-14

-13

-12

-11

1.00 1.25

1.50 1.75

2.00 2.25 2.50

/ T

D / m

-1

Fig. 1.16. Self-diﬀusion of several fcc metals versus reciprocal temperature nor-

malized to their melting temperatures T

normalized by its melting temperature T

(homologous temperature scale).

The following empirical rules for fcc metals are evident:

– Diﬀusivities near the melting temperature are similar for all fcc metals

and lie between about 10

−12

−1

and 10

−13

−1

– The Arrhenius lines on homologous scale have approximately the same

slope. Since the slope equals −∆H/RT

an empirical correlation between

the activation enthalpy ∆H and the melting temperature T

exists. This

can be stated as follows:

∆H ≈ (17 to 18)RT

. (1.59)

Equation (1.59) is sometimes denoted as the rule of van Liempt. The

melting temperature in (1.59) is expressed in Kelvin.

– The pre-exponential factors lie typically within the following range:

5 × 10

−6

−1

< 10

−3

−1

. (1.60)

For the explanation of the empirical rules the reader is referred to [48]. Ac-

tivation parameters for self-diﬀusion of some fcc metals are listed in Table 1.3

(for references see Chap. 2 in [6]). According to (1.57) the pre-exponential

factors of Table 1.3 correspond to self-diﬀusion entropies

34 Helmut Mehrer

Table 1.3. Activation parameters for self-diﬀusion in some fcc metals.

Metal Cu Ag Au Ni Pd Pt

∆H [kJ mol

−1

] 204 170 165 285 266 257

[10

−4

−1

] 0.35 0.046 0.027 1.77 0.205 0.05

∆S = S

+ S

(1.61)

of several R. According to (1.56) the activation enthalpy Q equals the sum of

formation and migration enthalpies of the vacancy. For fcc metals indepen-

dent experimental determinations of the formation and migration properties

show that

≤ 1 (1.62)

is fulﬁlled. For a review of point defect properties in metals the reader is

referred to [40].

1.8.2 Body-Centered Cubic Metals

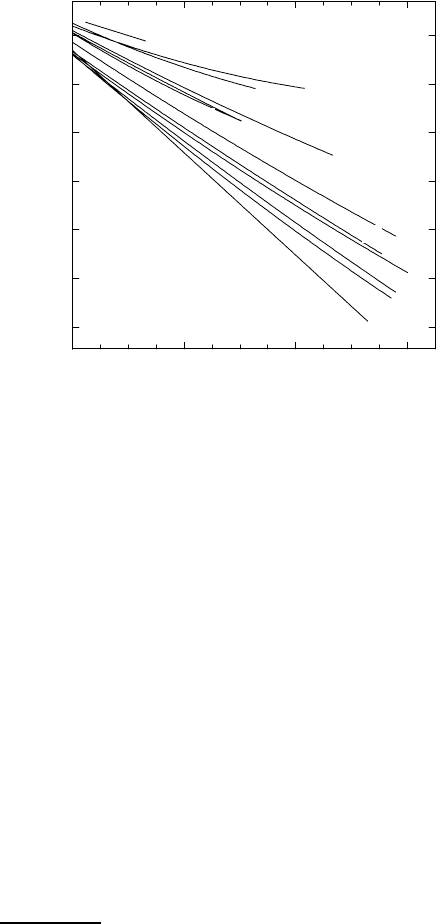
Self-diﬀusion coeﬃcients of several body-centered cubic (bcc) metals are

shown in the Arrhenius diagram of Fig. 1.17 on a homologous temperature

scale. A comparison of Figs. 1.17 and 1.16 reveals the following diﬀerences

between fcc and bcc metals:

– Diﬀusivities at homologous temperatures are usually higher for bcc metals

than for fcc metals. At the melting temperature T

the diﬀerence is about

one order of magnitude. Diﬀusivities for bcc metals near T

lie between

about 10

−11

−1

and 10

−12

−1

– The ‘spectrum’ of self-diﬀusivities is much wider for bcc metals than

for fcc metals. Self-diﬀusion is slowest for group VI metals and fastest

for group IV metals. It is interesting to note that the latter undergo

a structural phase transition from a hexagonal close-packed (hcp) low-

temperature to a bcc high-temperature phase.

– The Arrhenius diagram of self-diﬀusion for some bcc high-temperature

phases (β-titanium, β-zirconium) shows considerable upward curvature.

A common feature of fcc and bcc metals is that within one group of the

periodic table self-diﬀusion at homologous temperatures is slowest for the

lightest and fastest for the heaviest element of the group.

The very fast self-diﬀusion of bcc high-temperature phases and the wide

spectrum of diﬀusivities of bcc metals has been attributed to special fea-

tures of the lattice dynamics in bcc structures. A nearest-neighbour jump of

a self-atom in the bcc lattice is a jump in [111] direction. For bcc metals the

longitudinal phonon branch shows a minimum for 2/3[111] phonons, which is

1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 35

-23

-21

-19

-17

-15

-13

-11

1.0 1.4 1.8 2.2

β-Ti

β-Zr

-Hf

/ T

D / m

-1

Fig. 1.17. Self-diﬀusion of several bcc metals versus reciprocal temperature nor-

malized to their melting temperatures.

most pronounced for group IV metals. The associated low-phonon frequen-

cies indicate a small activation barrier for nearest-neighbour exchange jumps

between atom and vacancy [49, 50].

1.9 Impurity Diﬀusion in Metals

Let us now consider a very dilute substitutional binary alloy of metals A and

B with the mole fraction of B atoms much smaller than that of A atoms.

Then A is denoted as solvent (or matrix) and B is denoted as solute. Dif-

fusion in a dilute alloy has always two aspects: solute diﬀusion and solvent

diﬀusion. In this section we consider only solute diﬀusion in very dilute fcc

alloys

. This is often denoted as impurity diﬀusion. It implies that the solute

is isolated from other solutes in the matrix. In what follows we consider ﬁrst

the ‘normal’ behaviour of substitutional impurities. There are, however, some

remarkable exceptions from ‘normal’ impurity diﬀusion, which will be men-

tioned afterwards.

For solvent diﬀusion in dilute alloys the reader may consult [2,3].

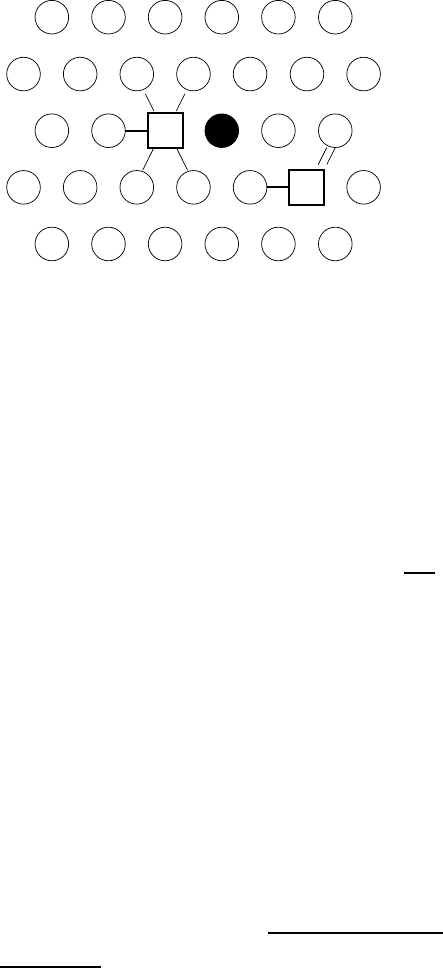
36 Helmut Mehrer









⇒

K 

 U

ωω

Fig. 1.18. Substitutional impurity diﬀusion in an fcc lattice: ‘ﬁve-frequency model’

for vacancy jumps in the presence of an impurity atom. Impurity (full circle), solvent

atoms (open circles), vacancy (squares).

1.9.1 ‘Normal’ Impurity Diﬀusion in fcc Metals

From the atomistic expression (1.41) derived in Sect. 1.6.1 and (1.44) we get

for the impurity diﬀusion coeﬃcient D

∗

(denoted in the following by D

)of

vacancy-mediated diﬀusion in cubic Bravais lattices

= f

exp





. (1.63)

To be speciﬁc we consider in the following fcc solvents

.Ifonlynearest-

neighbour interactions between vacancy and impurity occur, four vacancy

jump rates apart from the jump rate ω in the pure solvent must be considered.

This so-called ﬁve-frequency model introduced by Lidiard [51] is illustrated

in Fig. 1.18.

The jump rates of the vacancy are denoted as follows:

: jump rate for rotation of vacancy-solute complex,

: jump rate of vacancy-solute exchange,

: dissociation jump rate of vacancy-solute complex,

: association jump rate of vacancy-solute complex,

ω: vacancy jump rate in the pure solvent.

As shown by Manning [15], the correlation factor of impurity diﬀusion

can be written as

+(7/2)Fω

+ ω

+(7/2)Fω

, (1.64)

For impurity diﬀusion in bcc or hcp solvents see [2, 3].

We adopt the name ‘ﬁve-frequency model’ commonly used in the literature. The

physical meaning of the quantities ω

is that of jump rates.

1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 37

where F = F (ω/ω

) is a function of the rate ratio ω/ω

[15]. F approaches

unity for small ω

/ω. F =0.7357 for ω

= ω and F =2/7forlargeω

/ω.In

the case of self-diﬀusion all jump rates are equal. Then f

= f =0.7815 (see

Table 1.2). It is interesting to note that because of the condition of detailed

thermal equilibrium the relationship

=exp





(1.65)

must hold. This equation relates the dissociation and association rates of the

vacancy-solute complex to its Gibbs free energy of binding G

The impurity diﬀusion coeﬃcient (1.63) can be recast to give

= f

exp



− S

+ S



exp



−

− H

+ H



, (1.66)

where H

and S

denote binding enthalpy and entropy of the vacancy-solute

complex and H

and S

enthalpy and entropy of the vacancy-solute ex-

change jump. The activation enthalpy for impurity diﬀusion is then given

∆H

= H

− H

+ H

− C (1.67)

where the correlation term

C = R

∂ ln f

∂

(1.68)

results from the temperature dependence of the impurity diﬀusion correlation

factor.

It is evident from (1.55), (1.63), and (1.65) that the ratio of the diﬀusion

coeﬃcients between impurity- and self-diﬀusion can be written as

. (1.69)

This expression shows that the diﬀusion coeﬃcient D

of a substitutional

impurity diﬀers from that for self-diﬀusion D in the pure solvent for three

reasons:

–Thefactorω

/ω

shows that the probability to ﬁnd a vacancy on a

nearest-neighbour site of the impurity is diﬀerent from the equilibrium

vacancy concentration in the pure matrix because of vacancy-solute in-

teraction (1.65).

–Thefactorω

/ω arises because the exchange rate between vacancy and

impurity and those between vacancy and host atoms are diﬀerent.

–Thefactorf

/f arises because the correlation factor f

of impurity dif-

fusion is no longer a geometric factor as in the case of self-diﬀusion. It

depends on various jump rates and hence also on temperature.

38 Helmut Mehrer

-19

-18

-17

-16

-15

-14

-13

-12

-11

8 9 10 11

12 13

1200 1100 1000

900 800

= 12

-1

/ 10

-4

-1

D / m

-1

T / K

Fig. 1.19. Diﬀusion of several solutes and self-diﬀusion (dashed line) in silver.

Fig. 1.19 shows an Arrhenius diagram of various solutes in silver together

with silver self-diﬀusion (for references see Chap. 3 in [6]). It reveals charac-

teristic features of ‘normal’ diﬀusion of substitutional solute atoms:

–TheD

values of solutes lie in a relatively narrow band around self-

diﬀusion according to

1/100  D

/D  100. (1.70)

– The following empirical limits are found for pre-exponential factors

0.1 

(solute)

(self)

 10 (1.71)

and activation enthalpies

0.75 

∆H

(solute)

∆H(self)

 1.25. (1.72)

Substitutional solutes in other fcc solvents like Cu, Au, and Ni also conﬁrm

these limits (see Chap. 3 in [6] for references).

Since solute and solvent atoms are located on the same lattice and since

their diﬀusion is mediated by vacancies this rather small diﬀusivity disper-

sion is not surprising. It reﬂects the high eﬃciency of screening of point

charges in some metals (e.g. noble metals) which normally limits the vacancy-

impurity interaction enthalpy to values between 0.1 and 0.3 eV. Such values