Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 19

increased. Typical pressure eﬀects range from factors of 2 to 10 for a pressure

of 1 GPa (10 kbar). This variation is largely due to the fact that the Gibbs

free energy of activation ∆G varies with pressure according to

∆G = ∆H − T∆S = ∆E − T∆S+ p∆V (1.23)

where ∆V denotes the activation volume and ∆E the activation energy of

diﬀusion. Using (1.21) and (1.23) the Arrhenius equation (1.20) can also be

written as

D = D



exp



−

∆G



. (1.24)

Thermodynamics tells us that

∆V =



∂∆G

∂p



. (1.25)

Equation (1.25) can be considered as the deﬁnition of the activation volume.

Using (1.24) and (1.25) the activation volume can be obtained from mea-

surements of the diﬀusion coeﬃcient at constant temperature as a function

of pressure via

∆V = −RT



∂ ln D

∂p



+ RT

∂ ln D



∂p



 

correction term

. (1.26)

The term arising from the pressure dependence of D



can be estimated from

the isothermal compressibility and the Grueneisen constant of the material.

It is often negligibly small (a few percent of the molar volume V

or of the

atomic volume Ω = V

, respectively). Typical values for the activation

volume for various metals lie between 0.5 and 0.9 Ω. For a recent review

see [35].

We emphasize that a complete characterization of the diﬀusion process

requires knowledge of the three activation parameters ∆H = ∆E + p∆V

(valid for p =const.), ∆S and ∆V . For solids the term p∆V becomes signif-

icant only at high pressures. At ambient pressure it is negligible and hence

∆H ≈ ∆E.

1.6 Atomistic Description of Diﬀusion

1.6.1 Einstein-Smoluchowski Relation and Correlation Factor

Diﬀusion in crystalline solids takes place by a series of jumps of individual

atoms

. For interstitial diﬀusers the ‘diﬀusion lattice’ is formed by the in-

terstitial sites of the crystal lattice. Substitutional diﬀusers perform jumps

Near the melting temperature of fcc metals the self-diﬀusion coeﬃcient (see

Sect. 1.8) has a value of about 10

−12

−1

. This corresponds to about 10 million

jumps of each atom per second.

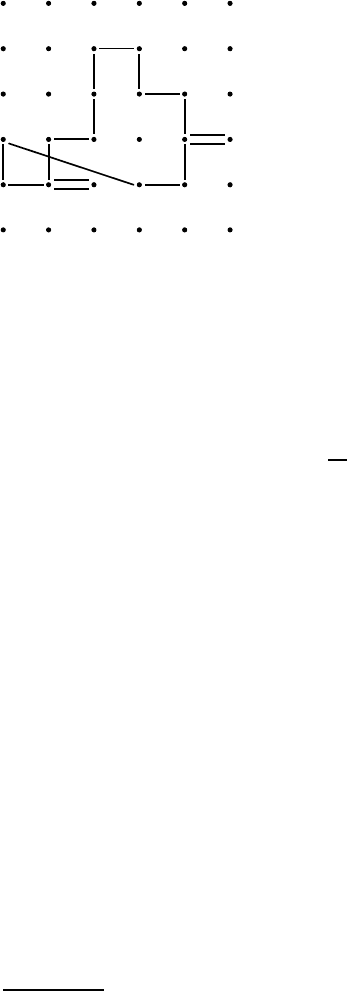
20 Helmut Mehrer



Fig. 1.6. Total displacement R of a particle on

a lattice composed of many individual jumps r

between sites of the normal lattice. The diﬀusivity on a lattice can be ex-

pressed in terms of physical quantities that describe the elementary jump

process. As we shall see below, these quantities are the jump length and the

jump rate.

The link between the displacement of particles on a (cubic) lattice and

the diﬀusion coeﬃcient is given by the relation

D =





(1.27)

where





denotes the mean square displacement of particles (see also

Chap. 18). Equation (1.27) is due to Einstein [36] and Smoluchowski [37].

It also includes correlation eﬀects as we shall see below.

Suppose that a particle carries out n jumps during time t. As illustrated

in Fig. 1.6 its total displacement

R =



i=1

(1.28)

is composed of n individual jump vectors r

and hence



i=1

n−1



i=1



j=i+1

. (1.29)

Taking the average over an ensemble of particles and using the fact that

the average of a sum of terms equals the sum of the averages of the terms we

get







i=1





n−1



i=1



j=i+1





. (1.30)

We restrict ourselves for reasons of simplicity to cubic lattices. The extension to

non-cubic lattices is straightforward and can be found, e.g., in [2].

1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 21

Correlation eﬀects are contained in the double sum of (1.30). For a true

random walk (index RW) the double sum in (1.30) vanishes as for every pair

one can ﬁnd another pair equal and opposite in sign. Then







i=1





. (1.31)

The degree of randomness in a long sequence of jumps can be expressed by

the so-called correlation factor f, which can be written as

f = lim

n→∞









= 1 + 2 lim

n→∞

n−1



i=1



j=i+1







i=1





. (1.32)

For diﬀusion on a lattice the jump vectors r

can take only a few deﬁnite

values. Let us consider a cubic coordination lattice with coordination number

Z and let us suppose that only nearest-neighbour jumps of equal length l

occur. Then (1.31) reduces to









, (1.33)

where





denotes the average number of jumps. For a true random walk (no

correlation) we get from (1.32) f = 1. It is convenient to deﬁne an average

jump rate of atoms into a certain direction, Γ ,by

Γ =





. (1.34)

The mean residence time τ of an atom on a certain lattice site is related to

the jump rate of the atom in a certain direction Γ via

τ =

ΓZ

. (1.35)

−1

is the mean atomic jump rate in any direction on a lattice. Then (1.27)

can be written as

D =

ZΓ =

6τ

, (1.36)

which is identical with (1.14) discussed in Sect. 1.3. Diﬀusion of interstitial

atoms in a dilute interstitial solution can be considered as a true random

walk process and hence (1.36) is an appropriate expression for the diﬀusion

coeﬃcient of interstitial diﬀusers.

Diﬀusion of self-atoms and of substitutional foreign atoms in metals,

metallic alloys, and in non-metallic solids is usually mediated by lattice va-

cancies. As already noticed by Bardeen and Herring [38] atoms migrating by

exchange with vacancies perform a correlated walk. The atom experiences

22 Helmut Mehrer

some ‘backward correlation’ since immediately after its exchange with the

vacancy the latter is still available for a backward hop of the atom. Then

the double sum in (1.30) does not vanish. For correlated diﬀusion on cubic

Bravais lattices

(1.36) must be replaced by

D =

ZΓ. (1.37)

In summary we can say that the diﬀusion coeﬃcient (in cubic crystals) for

interstitial diﬀusers as well as that for diﬀusers which migrate by exchange

with defects (vacancies, divacancies, self-interstitials, etc.) is described by

(1.37). For interstitial diﬀusers (in very dilute interstitial alloys) the corre-

lation factor is unity whereas for defect-mediated diﬀusion the correlation

factor is smaller than unity. Numerical values for the correlation factors of

self-diﬀusion can be found in Sect. 1.8. We emphasize that with increasing

degree of correlation the correlation factor decreases.

1.6.2 Atomic Jumps and Diﬀusion

Due to lattice vibrations atoms in a crystal oscillate around their equilibrium

positions with frequencies ν

of the order of the Debye frequency (typically

to 10

Hz). Usually an atom is conﬁned to a certain site by a potential

barrier of height G

, which corresponds to the Gibbs free energy diﬀerence

between the conﬁguration of the jumping atom at the saddle point and at

its equilibrium position. G

is denoted as Gibbs free energy of migration.

Diﬀusion is thermally activated which means that a ﬂuctuation of thermal

energy pushes the atom over the energy barrier between two neighbouring

sites.

Using statistical thermodynamics Vineyard showed [39] that the jump

rate ω, at which an atomic jump into an empty neighbouring site occurs, can

bewrittenintheform

ω = ν

exp



−



= ν

exp





exp



−



. (1.38)

On the right-hand side of (1.38) the Gibbs free energy according to

= H

− TS

(1.39)

is decomposed into enthalpy H

and entropy S

of migration (superscript

M).

A diﬀusion jump of a self-atom or of a substitutional solute atom will only

occur if a neighbouring lattice site is occupied by a vacancy. If p denotes the

vacancy availability factor (the probability that the neighbouring site of the

For an extension to non-cubic lattices see, e.g., [2].

1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 23

jumping atom is empty) the jump rate of the atom to this particular site is

given by

Γ = ωp. (1.40)

Inserting this expression into (1.37) yields

D =

Zωp. (1.41)

For interstitial diﬀusion in a very dilute interstitial alloy we have f =1,

p =1,andΓ ≡ ω. Then (1.41) reduces to (1.36).

1.6.3 Diﬀusion Mechanisms

Solid-state physics tells us that atoms in crystals oscillate around their equi-

librium positions. Occasionally these oscillations become large enough to al-

low an atom to change its site. As outlined above these jumps give rise to

diﬀusion in solids. Various atomic mechanisms of diﬀusion in crystals have

been identiﬁed and are catalogued in what follows:

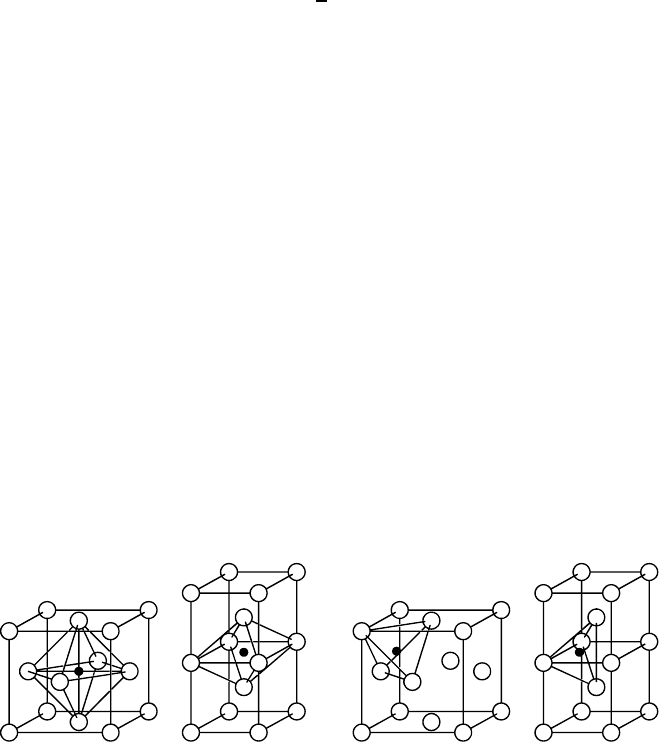
Interstitial Mechanism

Solute atoms which are considerably smaller than the solvent (lattice)

atoms (e.g. hydrogen, carbon, nitrogen, and oxygen) are usually incorpo-

rated in interstitial sites of a metal. In this way an interstitial solid solution

is formed. Interstitial solutes usually occupy octahedral or tetrahedral sites

of the lattice. Octahedral and tetrahedral interstitial sites in the fcc and bcc

lattices are illustrated in Fig. 1.7. Interstitial solutes can diﬀuse by jumping

from one interstitial site to the next as shown in Fig. 1.8. This mechanism

is sometimes also denoted as direct interstitial mechanism in order to distin-

guish it more clearly from the interstitialcy mechanism discussed below.

(a) (b)

Fig. 1.7. Octahedral (a) and tetrahedral (b) interstitial sites in the fcc (left) and

bcc (right) lattice. Lattice atoms (open circles); interstitial sites (full circles).

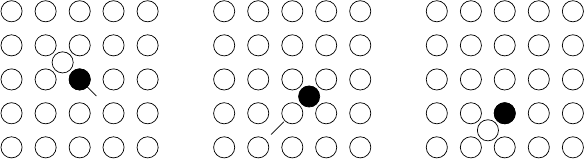
Vacancy Mechanism

Self-atoms or substitutional solute atoms migrate by jumping into a neigh-

bouring vacant site as illustrated in Fig. 1.9. In thermal equilibrium the

atomic fraction of vacancies C

in a monoatomic crystal is given by

24 Helmut Mehrer



Fig. 1.8. Direct interstitial

mechanism of diﬀusion.

⇒

Fig. 1.9. Vacancy mechanism of diﬀu-

sion.

⇒

Fig. 1.10. Divacancy mechanism of dif-

fusion.

=exp





exp



−



, (1.42)

where S

and H

denote formation entropy and enthalpy of a vacancy (super-

script F ). For self-diﬀusion the vacancy availability factor p in (1.40) equals

. Typical values for C

near the melting temperature of metallic elements

lie between 10

−4

and 10

−3

(in molar fractions) [40]. From (1.38), (1.40), and

(1.42) we get for the jump rate of an atom in the case of self-diﬀusion

Γ = ν

exp



+ S



exp



−

+ H



. (1.43)

Self-diﬀusion in metals and alloys, in many ionic crystals (e.g. alkali halides)

and ceramic materials occurs by the vacancy mechanism.

Attractive or repulsive interactions modify the probability to ﬁnd a va-

cancy on a nearest-neighbour site of a solute atom. For a very dilute sub-

stitutional solution the probability p of ﬁnding a vacancy next to the solute

atom is given by

p = C

exp





, (1.44)

where G

denotes the Gibbs free energy of binding between vacancy and

solute (superscript B). The quantity G

−G

can be considered as the Gibbs

free energy for the formation of a vacancy on a nearest neighbour site of

the foreign atom. For attractive interaction (G

> 0) p is enhanced and for

repulsive interaction (G

< 0) p is reduced compared to the equilibrium site

fraction of vacancies C

in a pure solvent

Note the convention: The binding energy is positive for attractive interaction.

1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 25

Divacancy Mechanism

Diﬀusion of self-atoms or substitutional solute atoms can also occur via

bound pairs of vacancies (denoted as divacancies or as vacancy pairs) as

illustrated in Fig. 1.10. At thermal equilibrium divacancies in an elemental

crystal are formed from monovacancies according to the reaction

V+V 2V . (1.45)

As a consequence of the law of mass action we have for the mole fractions

and C

of mono- and divacancies

= K (C

)

. (1.46)

The quantity K contains the Gibbs free binding energy of the vacancy pair.

Since the monovacancy population under equilibrium conditions increases

with temperature, the concentration of divacancies C

becomes more sig-

niﬁcant at high temperatures. Divacancies in fcc metals have a higher mo-

bility than monovacancies [40]. Therefore self-diﬀusion of fcc metals usually

has some divacancy contribution in addition to the vacancy mechanism. The

latter is, however, the dominating mechanism at temperatures below 2/3of

the melting temperature [22].

Interstitialcy Mechanism

In this case self-interstitials – extra atoms located between lattice sites –

act as diﬀusion vehicles. As illustrated in Fig. 1.11 a self-interstitial replaces

an atom on a substitutional site which then replaces again a neighbouring

lattice atom. Self-interstitials are responsible for diﬀusion in the silver sublat-

tice of silver halides. In silicon, the base material of microelectronic devices,

the interstitialcy mechanism dominates self-diﬀusion and plays a prominent

role in the diﬀusion of some solute atoms including important doping ele-

ments [41]. This is not surprising since the diamond lattice (coordination

number 4) provides suﬃcient space for interstitial species. For a detailed dis-

cussion of the diﬀusion mechanism in Si see Chap. 4, Sect. 3.

In densely packed metals contributions of this mechanism are negligible

for thermal diﬀusion. Self-interstitials in metals have a fairly high formation

enthalpy compared to vacancies [40]. Therefore the concentration of the lat-

ter is dominating completely under equilibrium conditions. The interstitialcy



Fig. 1.11. Interstitialcy mechanism of diﬀusion.

26 Helmut Mehrer

mechanism is, however, important for radiation induced diﬀusion, since then

self-interstitials and vacancies are created in equal numbers by irradiation of

a crystal with energetic particles.

Interstitial-Substitutional Exchange Mechanisms

Some solute atoms (B) can be dissolved on interstitial (B

) and substi-

tutional sites (B

) of a solvent crystal (A) and diﬀuse via an interstitial-

substitutional exchange mechanism (see Fig. 1.12). For some of these so-called

‘hybride solutes’ the diﬀusivity of B

is much higher than the diﬀusivity of B

whereas the opposite is true for the solubilities. Under such conditions the

incorporation of B atoms can occur by the fast diﬀusion of B

and the sub-

sequent change-over to B

. Two types of interstitial-substitutional exchange

mechanisms can be distinguished:

If the change-over involves vacancies (V) according to

+V B

(1.47)

the mechanism is denoted as dissociative mechanism (sometimes also: Frank-

Turnbull mechanism or Longini mechanism). The rapid diﬀusion of Cu in

germanium (see Chap. 4, Sect. 4.3) and of some foreign metallic elements in

polyvalent metals such as lead, tin, niobium, titanium, and zirconium has

been attributed to this mechanism (see Sect. 1.9).

If the change-over involves self-interstitials (A

) according to

 B

(1.48)

the mechanism is denoted as kick-out mechanism. The fast diﬀusion of Au, Pt

and Zn in silicon has been attributed to this mechanism [41,42] (see Chap. 4,

Sect. 4.3).

For a description of diﬀusion processes, which involve interstitial-substitu-

tional exchange reactions, Fick’s equations must be supplemented by reaction

- -



i V V





i V

Fig. 1.12. Interstitial-substitutional exchange mechanisms of foreign atom diﬀu-

sion. Upper part: dissociative mechanism. Lower part: kick-out mechanism.

1 Diﬀusion: Introduction and Case Studies in Metals and Binary Alloys 27

terms. Since three species are involved, sets of three coupled diﬀusion-reaction

equations result for both mechanisms mentioned above. Solutions of these

equations – apart from a few (interesting) special cases – can only be ob-

tained by numerical methods. For details we refer the reader to the literature

(e.g. [41,42]).

In the following four sections we consider examples of normal interstitial

diﬀusion, diﬀusion of hydrogen, self-diﬀusion in pure metals, and of impurity

diﬀusion in metals

. We shall see below that the Arrhenius parameters of

(1.20) can be readily interpreted in terms of properties of atomic defects.

1.7 Interstitial Diﬀusion in Metals

1.7.1 ‘Normal’ Interstitial Solutes

Carbon, nitrogen, and oxygen often form interstitial solid solutions with met-

als. Interstitial sites in fcc and bcc lattices are illustrated in Fig. 1.7. Inter-

stitial diﬀusers have diﬀusion coeﬃcients that are much larger than those

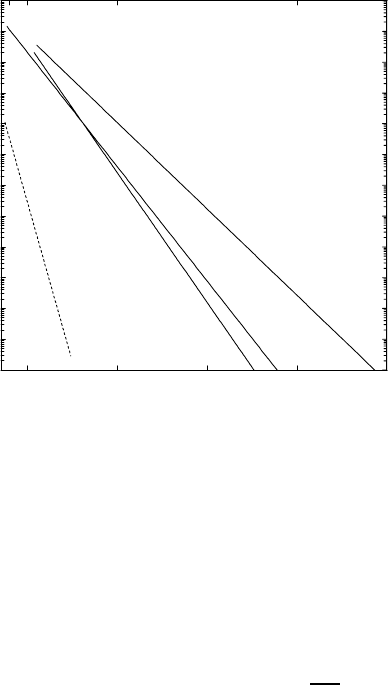
of self- and substitutional solute diﬀusion. Examples are shown in Fig. 1.13,

where diﬀusion of C, N, and O in niobium is displayed together with nio-

bium self-diﬀusion. The pertaining activation enthalpies and pre-exponential

factors are collected in Table 1.1 (for references see Chap. 8 in [6]).

Table 1.1. Activation parameters of some solutes in niobium (for references see [6]).

Diﬀuser C N O Nb

∆H [kJmol

−1

] 142 161 107 395

−1

]1× 10

−6

6.3 × 10

−6

4.2 × 10

−7

5.2 × 10

−5

For a dilute interstitial alloy the probability p in (1.40) is unity. The

magnitude of the activation enthalpy is also small with the result that the

diﬀusion coeﬃcients for interstitial diﬀusion are many orders of magnitude

larger than those for self-diﬀusion of lattice atoms. Interstitial diﬀusivities

near the melting temperature of the solvent can be as high as diﬀusivities in

liquids.

For interstitial solutes, which migrate by the direct interstitial mechanism,

(1.36) can be written as

D = ga

exp





exp



−



. (1.49)

Here a is the cubic lattice parameter and g a geometric factor, which depends

on the lattice geometry and on the type of interstitial sites (octahedral or

For reasons of simplicity we restrict ourselves to cubic crystals.

28 Helmut Mehrer

-20

-18

-16

-14

-12

-10

-8

5 10

15 20 25

2000 1000

500

-1

/ 10

-4

-1

D / m

-1

T / K

Fig. 1.13. Diﬀusion of C, N, O and Nb in niobium.

tetrahedral) occupied by the solute. For octahedral sites (Fig. 1.7) we have

g = 1 for the fcc lattice and g =1/6 for the bcc lattice. For interstitial

diﬀusers the Arrhenius parameters of (1.20) have the following meaning:

∆H = H

(1.50)

and

= ga

exp





. (1.51)

With reasonable values for the migration entropy (between zero and several

R) and the attempt frequency (between 10

and 10

−1

) (1.51) yields the

following limits for the pre-exponential factors of interstitial solutes:

−7

−1

≤ D

≤ 10

−5

−1

. (1.52)

The experimental values of Table 1.1 conﬁrm this estimate.

The fast diﬀusion of C, N, and O and the fact that N

and O

are gases, or,

in the case of carbon, readily available in gas or vapour form (CO

,CH

,...)

have an impact on the choice and availability of methods used to measure

their diﬀusion coeﬃcients. Anelastic relaxation, magnetic relaxation (in the

case of ferromagnetic materials), internal friction, steady-state and in- and

out-diﬀusion methods are often applied. For details the reader is referred to

textbooks [2,3].