Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

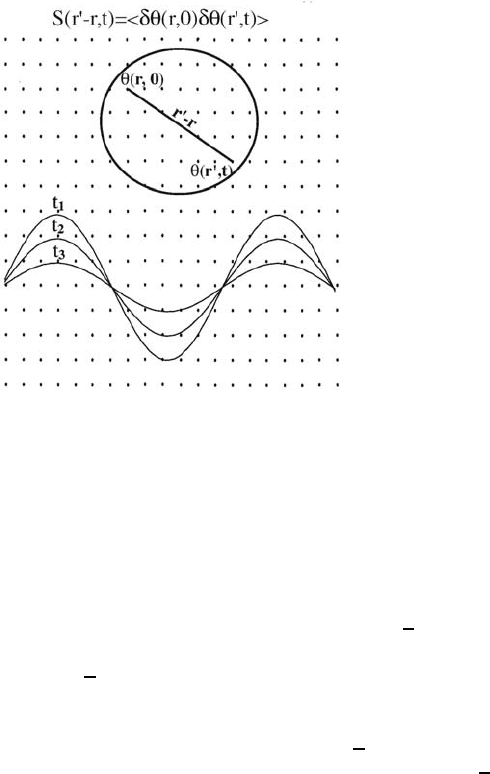
7 Fluctuations and Growth Phenomena in Surface Diﬀusion 293

Fig. 7.3. Schematic presenta-

tion of the diﬀusion experiment

to measure the decay of coverage

ﬂuctuations within a probe area

(upper part). Presentation of

the grating experiment when an

initial sinusoidal coverage pro-

ﬁle decays exponentially in time

(lower part).

Since only one spatial Fourier component of wavevector k is present, both

S(k, t) and the amplitude of the coverage variation δθ(t) decay exponentially

according to (7.6). The time constant τ of the decay can be used to deduce the

value of the diﬀusion coeﬃcient D

=(2π/k)

/τ. Experimentally a method

based on (7.6) has been implemented by forming a 1D grating from the in-

terference of two laser beams incident on the same surface spot [13]. Atoms

within the illuminated region desorb according to the local laser power which

varies sinusoidally because of the interference of the two waves. So within the

grating the coverage is lower than the average

θ. Diﬀusion of atoms from the

surrounding area reﬁlls the grating and returns the coverage back to its aver-

age value

θ. The reﬁlling is measured in time by using a third low power laser

which monitors the decaying second harmonic generation (SHG) or the ﬁrst

order diﬀraction signal, as the grating reﬁlls in time. Although the coverage

within the 1D grating is always below

θ (while in the case of the oscilla-

tory chemical potential the coverage oscillates around

θ) its reﬁlling follows

a similar time dependence as (7.6).

Equation (7.7) can be implemented in the frequency domain with a spec-

troscopic technique to measure S(k, ω). This technique is a well-developed

method to measure diﬀusion coeﬃcients in 3D systems with the use of qua-

sielastic neutron scattering (see Chap. 3). The equivalent technique in two

dimensions is quasielastic He-scattering which fulﬁlls the necessary require-

ments to have both wavevector and energy resolution [14]. A monochro-

matic beam of He-atoms scatters from the surface with momentum transfer

wavevector k and the scattered atoms are energy resolved to obtain the spec-

trum S(k, ω) (of (7.7)). The energy loss of the atom beam at ﬁxed wavevector

k is measured from the full width at half maximum (FWHM) of the quasi-

294 Michael C. Tringides and Myron Hupalo

elastic spectra ∆E = ∆ω (extracted after ﬁtting the experimental spec-

tra to Lorentzian lineshapes). The inverse ∆ω

−1

corresponds to the time

∆t =(D

)

−1

for the diﬀusing atom to reach a distance of about λ =2π/k.

For “hydrodynamic” (i.e. long wavelength) diﬀusion measurements, (espe-

cially at high coverage for systems with interactions when D

can diﬀer from

the one deduced at smaller length or time scales) it is necessary to perform the

measurements at suﬃciently small wavevectors k and long scattering times

∆ω

−1

being larger than the time for a time to the nearest neighbor site. This

imposes strong requirements on the wavevector and energy resolution of the

technique.

Diﬀusion in Externally Imposed Concentration Gradients

Other methods to measure surface diﬀusion are carried out under conditions

when the coverage gradient ∂θ/∂r is externally imposed. For example, in 1D

step proﬁle evolution experiments along a line r the coverage has one value

in region r<0andadiﬀerentvalueθ

in region r>0. With time, atoms

will move from the region of higher to the region of lower coverage (shown

schematically in Fig. 7.4) until a uniform concentration is established. If there

are no adatom interactions (except site exclusion) the proﬁle is described by

θ(r, t)=

(θ

− θ

)



1 − erf



(



. (7.9)

Such proﬁle experiments result in coverage independent D

values in agree-

ment with equilibrium methods.

In systems with interactions the coverage dependence D

(θ) is obtained

from the Boltzmann-Matano (BM) analysis (see Chap. 1, Sect. 1.11.1) of the

proﬁle shape. However, before applying the method to the experimental or

simulation results, it is essential to show ﬁrst that the proﬁles scale (i.e. they

canbewrittenintheformθ(r, t)=θ(r/t

0.5

)). It is not possible to satisfy

the scaling condition in the case of an initial 2D patch geometry [15]. If

the scaling condition is met, D

(θ

) is obtained for a range of coverages θ

(θ

<θ

)by

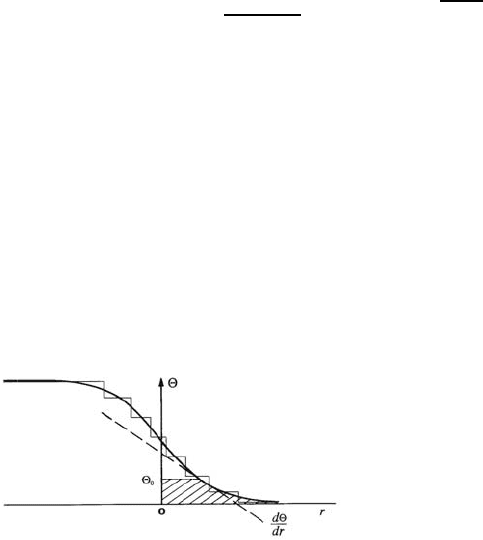
Fig. 7.4. Schematic representa-

tion of a step-proﬁle evolution ex-

periment and the geometric pa-

rameters (shaded integrated area

and local slope) needed to eval-

uate the Boltzmann-Matano in-

tegral (7.10). Each ﬂat segment

of constant coverage can approx-

imately be thought to be at equi-

librium.

7 Fluctuations and Growth Phenomena in Surface Diﬀusion 295

(θ



dθ





r dθ. (7.10)

If the scaling condition is not fulﬁlled, a time-dependent diﬀusion coeﬃ-

cient will be extracted from (7.10) where the value obtained at the earliest

times deviates the most from the equilibrium value. At longer times the pro-

ﬁle smoothes out, the gradient ∂θ/∂r is reduced, the coverage diﬀerences are

smaller and the scaling condition is met more easily.

We can consider limits in the steepness of the gradient ∂θ/∂r,soD

(θ)

extracted from proﬁle evolution experiments agrees with D

(θ) obtained at

equilibrium [16]. For a given system the gradient ∂θ/∂r must not exceed a

certain maximum value to ensure that the externally imposed ﬂuctuations

(from the initial steepness of the proﬁle) do not exceed the thermodynami-

cally generated ﬂuctuations. The proﬁle can be approximated as a staircase

of ﬂat segments of length L,(withL ≈ 5L

res

, i. e. equal to several times the

optimal spatial resolution limit L

res

≈ 0.1 µm) for reliable diﬀerentiation. It

is necessary that the externally imposed gradient (∆θ/∆r)

exp

is smaller than

the coverage gradient due to mean square ﬂuctuations within a system of size

L. The coverage variation (∆θ)

therm

is simply given by the ratio of the mean

square ﬂuctuations δN

(0)

0.5

and the number of sites (L/a

)(witha

the

lattice constant). This ratio, in turn, is simply the normalized compressibility

of the system. We thus have

(∆θ)

therm

= δN

(0)

0.5

/(L/a

)=(∂θ/∂(µ/k

T ))

0.5

. (7.11)

It follows that the condition

(∆θ/∆r)

exp

< (∆θ/∆r)

therm

=(∂θ/∂(µ/k

T ))

0.5

/L (7.12)

between the experimental and the thermodynamically generated gradient

should hold for the extracted D

(θ) to be the same as the equilibrium

one. Equation (7.12) most probably will not be satisﬁed at early times

when (∆θ/∆r)

exp

has its largest value of about θ/L (in practise larger

than 10

θ/cm). This value is comparable to the right-hand side of (7.12), at

least for the case of the Langmuir gas (i. e. site exclusion interaction) when

∂θ/∂(µ/k

T )=θ(1 − θ) < 1. Even at later times (7.12) can be violated

close to the ideal coverage of an ordered phase (i.e. at θ =0.5ML for the

p(2 × 1) phase and for T<T

the phase is least compressible, which means

∂θ/∂(µ/k

T ) → 0).

This discussion explains a recent Monte Carlo study of O/W(110) with

the p(2×1) the ordered phase from step proﬁle evolution with the BM method

[17]. In these simulations the larger deviation between the D

extracted from

BM and equilibrium methods was observed at early times and for a coverage

close to θ =0.5ML.

The BM step proﬁle method should fail to follow critical ﬂuctuations as

T → T

and ∂θ/∂(µ/k

T ) →∞, since ﬁnite size eﬀects become important,

296 Michael C. Tringides and Myron Hupalo

especially at early times when the constant coverage segments in Fig. 7.4 are

the smallest. Smaller “subsystems” cannot measure correctly thermodynamic

singularities of the free energy or its derivatives.

One of the major predictions in the variation of D

(θ, T ) is the critical

slowing down close to a second-order phase transition [18]. This is easily seen

from a widely used mean ﬁeld expression for the diﬀusion coeﬃcient, namely

= Γa

/(∂ ln θ/∂(µ/k

T )) with Γ denoting the average jump rate. This

expression is referred to also as the Darken equation when Γa

is identiﬁed

with the tracer diﬀusion coeﬃcient D

(cf., e. g., Chap. 1, Sect. 1.11.2). Close

to a second-order phase transition, critical ﬂuctuations generated thermody-

namically are so large (∂µ/∂θ →∞as T → T

) that no diﬀusion currents

can eliminate them. This eﬀectively means that D

(T )goesto0asT → T

Strictly speaking this is true for systems where the order parameter is the

coverage θ, since only then the compressibility ∂µ/∂θ is singular at T

.How-

ever, for systems which have order parameters diﬀerent from θ (e. g. an Ising

model with repulsive interactions and the order parameter being the “stag-

gered magnetization”) a weaker singularity is expected for (∂θ/∂µ)

−1

at the

phase transition. Critical slowing down eﬀects both in equilibrium and proﬁle

evolution methods should be smeared out, since only the “staggered” com-

pressibility (i.e. the inverse derivative of the order parameter with respect

to µ) is truly singular. However, D

is still reduced close to T

as a result

of the less singular behavior of ∂µ/∂θ (as will be seen later in Sect. 7.3.2

in connection with Fig. 7.9). In addition to the temperature dependence of

close to a phase transition, the coverage dependence D

vs θ (for ﬁxed

temperature T<T

) can show maxima as the ideal coverage of the ordered

phase θ → θ

is approached, since at θ

the perfect defect-free phase is least

compressible. The reason is that large energy is needed to generate deviations

from this ideal phase, i.e. ∂θ/∂µ → 0asθ → θ

. For the Ising model with

repulsive interactions at θ

=0.5 (the coverage of the c(2 × 2) phase) D

shows a maximum both in equilibrium and proﬁle evolution methods [19,20].

Clearly the behaviour of D

, whether it shows maxima or minima, depends

on the interaction Hamiltonian (i. e. the nature of the order parameter) and

the control parameters, i. e. temperature and coverage. Step proﬁle evolution

methods have been used in [21] to study phase transitions.

In addition to the interest in proﬁle evolution measurements of surface

diﬀusion, non-equilibrium methods based in the time evolution of a system

from a disordered to an ordered phase after a deep quench have been reviewed

in [22] and will not be covered here. Instead we will discuss the role of surface

diﬀusion in epitaxial growth because it has more technological signiﬁcance.

Since epitaxial growth is commonly carried out at far-from-equilibrium condi-

tions (i.e. low temperatures or high deposition rates) the observed structures

are metastable [1]. These epitaxially grown structures can have technological

importance when they are regular in size, shape and separation. In general,

many diﬀerent microscopic processes with diﬀerent activation barriers can

7 Fluctuations and Growth Phenomena in Surface Diﬀusion 297

operate during the growth. As discussed earlier, at low temperatures the

process with the lowest barrier is the controlling one.

We present below speciﬁc examples for equilibrium and non-equilibrium

experiments to illustrate the previous general discussion. The equilibrium ex-

periments are based on measuring coverage ﬂuctuations with high resolution

low energy electron diﬀraction (HLEED) on stepped Si(100) and with STM.

As for non-equilibrium experiments, we discuss the formation of Pb islands

of uniform height, ﬂat tops and steep edges on Si(111) and measurements of

interlayer diﬀusion on Ag/Ag(111).

7.3 Equilibrium Measurements of Surface Diﬀusion

7.3.1 Equilibrium Diﬀusion Measurements

from Diﬀraction Intensity Fluctuations

Are Diﬀraction Intensity Fluctuations Possible?

Experiments measuring diﬀusion at equilibrium are based on coverage ﬂuc-

tuations which have a low amplitude for systems truly at equilibrium. If the

ﬂuctuations are large, as discussed for step proﬁle evolution experiments, they

introduce a non-thermodynamic driving force in the diﬀusion current and the

extracted parameters cannot always be compared to the ones from equilib-

rium experiments. However, ﬂuctuations of low amplitude imply that the

measurable signal is small and it is necessary for the experimental technique

to have suﬃcient ampliﬁcation. Such a ﬂuctuation method has been imple-

mented with great success by exploiting the high magniﬁcation (≈ 10

)of

the ﬁeld emission microscope [11,16] to monitor the time dependence of cov-

erage ﬂuctuations within a probe area, as discussed in connection with (7.8).

Since it is reviewed elsewhere it will not be discussed further in this chapter.

An STM based probe area method [22, 23] will be described in Sect. 7.3.2.

The electron emission process requires high electric ﬁelds (typically 0.5 V/

which can potentially introduce bias to the random walk with atoms prefer-

entially diﬀusing towards the tip.

Despite the success of these methods, there are reasons to develop a

reciprocal-space method (i.e., surface diﬀraction) to measure equilibrium ﬂuc-

tuations. In addition to the disadvantages associated with the presence of an

electric ﬁeld, real space methods have to integrate over the atoms occupy-

ing the probe area (cf (7.8)) and therefore are not sensitive to the state of

the overlayer, i. e. are unable to decide whether it is an ordered or disor-

dered phase. On the other hand, diﬀraction-based methods are wavevector

selective and therefore sensitive to the ﬂuctuations within a speciﬁc phase,

when the overlayer supports the formation of diﬀerent phases. By “tuning”

the wavevector to the phase of interest the sensitivity of the technique is

enhanced. In such methods ﬂuctuations of the diﬀracted intensity deﬁned by

298 Michael C. Tringides and Myron Hupalo

I(k, t)=

(Nθ)



θ(r, t)θ(r



+ r, t)exp(−kr)d



r (7.13)

are measured which are more intimately related to theoretical quantities like,

e. g., S(k, t) (cf. (7.6)). The autocorrelation function of I(k, t) is deﬁned in

terms of ﬂuctuations δI(k, t)=I(k, t) −I(k, t) from the average value

I(k, t) at time t. Although it involves 4-point correlation functions, as shown

in [24], it can be expressed in terms of the structure factor S(k, t)

G(k, t)=δI(k, 0)δI(k, t) = cS

(k, t) (7.14)

with c representing a constant which depends on the details of the system

under investigation. Measurements of the autocorrelation function of I(k, t)

provide a new method of measuring S(k, t) [25–28].

The idea of the diﬀraction experiment is straightforward but it has not

been implemented earlier because several demanding experimental conditions

should be met [25, 26]: (i) coherence in the diﬀraction experiments extends

up to a ﬁnite distance ζ, so that the intensity ﬂuctuations are correlated

only up to this distance. Since the beam size d is larger than ζ it includes

(d/ζ)

incoherent scattering regions and the ﬂuctuation signal is reduced

since temporal correlations between diﬀerent regions are lost. To minimize

this eﬀect it is necessary to employ high-resolution diﬀractometers (i.e ∆k

better than 0.1% of the Brillouin Zone) or small d. The high resolution has

the additional advantage of prohibiting the integration of the measured time

constant τ(k) over a wider wavevector range. (ii) it is also essential to have

high acquisition speed to take full advantage of the high resolution, otherwise

a larger time constant than the true one will be extracted, a severe problem

at high temperatures.

As shown recently [25, 26] condition (i) depends on the brightness of the

incident beam (i.e. number of electrons per solid angle per time). It is met

with specialized electron guns of high current densities. The use of such guns

and modern high-gain channeltron-based detectors has shown the feasibility

of the technique, as discussed below in diﬀraction experiments on stepped

surfaces.

Fluctuation measurements have been also pursued in “speckle” X-ray ex-

periments [29] where the incident beam size is reduced to size comparable to

the coherence length d ∼ ζ with the use of µm size geometric apertures. Such

a stringent condition is necessary for “speckle” measurements (i. e. when the

relative scattering phase of all the atoms within the illuminated region is pre-

served). Features of the static structure factor S(k) (i. e. interference fringes)

have a one-to-one correspondence with the exact location of the atoms within

the illuminated area, which eﬀectively enables the technique to function like

a real space “microscope”. However, such reduction of beam size is not neces-

sarily beneﬁcial for time-dependent ﬂuctuation measurements, if the bright-

ness of the source (i. e. number of photons per area per second) remains the

same after the aperture is introduced. Because of the reduced beam size, the

7 Fluctuations and Growth Phenomena in Surface Diﬀusion 299

incident photon ﬂux will be correspondingly reduced which also lowers the

measurable signal.

Thermal Fluctuations at Steps

What kind of dynamic processes can be studied from diﬀraction intensity ﬂuc-

tuations? As the simplest example we can think of point defects or adatoms

diﬀusing on the surface, with atomic scattering factors diﬀerent from the

one of the substrate atoms f

= f

. As the adatoms diﬀuse their position

and scattering phase is time-dependent (f

(r, t)), which will cause ﬂuctua-

tions in the diﬀracted intensity I(k, t)=|



exp(ikr)|

. The autocorre-

lation function of the intensity ﬂuctuations will decay with time constant

τ(k)=(2π/k)

/4D

where D

is the adatom diﬀusion coeﬃcient. Such low

coverage experiments can be best performed with He-scattering since the

adatom scattering factor can diﬀer substantially from the substrate scatter-

ing factor [30] thus maximizing the measured signal. In a diﬀerent experi-

ment, ﬂuctuation measurements can be used to study the dynamics close to

phase transitions. This is an area where practically no experimental work

has been done so far in 2D systems. Close to a second-order phase transi-

tion, large ﬂuctuations of the order parameter (i.e. superstructure intensity)

at the ordering wavevector are expected. Changes in the functional form of

the time-dependent correlation function, critical slowing down and dynamical

critical exponents can be measured from the superstructure spot ﬂuctuations.

Another example are physisorbed systems (i.e. inert gases adsorbed at low

temperatures) with ﬂuctuations in the intensity of integer order spots, origi-

nating either from adatom diﬀusion or adsorption-desorption from or to the

gas phase. As shown in [24], the form of the autocorrelation function changes

as the relative contribution of the two processes, diﬀusion and desorption, is

varied with temperature. In such experiments the autocorrelation function

measured at diﬀerent temperatures can be used to deduce the barriers of

the two processes, i.e. the desorption energy, the corrugation of the potential

energy surface in the limit θ → 0 and the adatom interactions.

In general, for any microscopic process monitored with diﬀraction ﬂuctu-

ations of I(k, t), the ﬁrst theoretical priority is to work out the form of the

autocorrelation function to check if it agrees with the measured one. Such

comparison can be used to deduce the details of the microscopic mechanism

controlling the dynamic process and to measure in real time the relevant

time constants. Both pieces of information are diﬃcult to obtain with other

methods.

A full comparison between theoretical and experimental results has been

carried out in the dynamics of thermally induced step ﬂuctuations [27, 28].

When steps are heated to higher temperatures they deviate from their

straight positions because a ﬂuctuating step leads to a gain in entropy. Ele-

mentary excitations such as kinks, vacancies etc. are created which are highly

mobile and cause the ﬂuctuations. Dynamic measurements of the ﬂuctuations

300 Michael C. Tringides and Myron Hupalo

can be used to determine the type of microscopic process generating them

and the relevant energetic barriers.

Step ﬂuctuations result from several competing processes described in

[31]. Step mobility Γ (T ) is responsible for generating thermal excitations at

temperature T . This is opposed by the restoring force acting to return the step

back to its straight position. The restoring force consists of two terms. First,

the step stiﬀness

β describes the energy cost to generate a kink on a straight

step, since a kink atom has lower coordination than an atom at a straight step.

Second, long-range step-step interactions described in terms of an eﬀective

potential U(x)(wherex is the separation between two steps) constraints the

step to maintain the initial terrace length L. Excursions of the step separation

from L will increase the potential energy U(x) and as a result the elastic

forces between the steps act to restore the step back to its straight position.

This second component of the restoring force is parametrized by the “force

constant” of the potential c = ∂

U/∂x

evaluated at the initial average

terrace size L. The two parameters of the restoring force

β and c determine

the step average equilibrium properties: the mean square displacement w

∞



−x)

(where (x

−x) is the deviation of the ith atom from its average

position), the correlation length ξ along the step (deﬁned by the correlation

function C(y) ∼ exp(−|y|/ξ) between two atoms separated by distance y)

and

β the step-stiﬀness

∞

= k



8cβ



1/2

,ξ(T )=





1/2

. (7.15)

The Cartesian coordinate system is chosen in such a way that z is normal

to the terrace and x, y lie on the terrace, with x normal to the step and y along

the step. Both w

∞

and ξ can be extracted from ﬁts of the static intensity

proﬁle I(k

) at the out-of-phase condition k

= (odd) π/d =(2l +1)π/d,

where d is the step height and l an integer. At the out-of-phase condition,

neighboring terraces scatter destructively because the phase diﬀerence of the

scattered wave normal to the terrace is an odd multiple of π and therefore

I(k,t) is maximally sensitive to step ﬂuctuations. The static diﬀraction proﬁle

of an integer order beam normal to the step I(k

) is split with the separation

between the two split spots (located at k

= ±π/L) proportional to the

inverse of the average terrace length. The FWHM of each split spot in the

x direction can be used to extract w

∞

. On the other hand the static proﬁle

along the step I(k

) is sensitive to correlations in the atom positions and

in the step ﬂuctuations up to the correlation length ξ(T ) [28]. The inverse

of the FWHM of spot proﬁle along the spot for ﬁxed out-of-phase values of

= ±π/L (at the two maxima of the split spot) can be used to deduce the

correlation length ξ(T ) along the step.

Temporal step ﬂuctuations are measured by monitoring the peak of the

diﬀracted intensity at the maxima of the out-of-phase split spot I(k

±π/L, k

= 0). At in-phase-conditions, k

= (even)π =2lπ/d, no ﬂuctua-

7 Fluctuations and Growth Phenomena in Surface Diﬀusion 301

tions (and no splitting of the proﬁle I(k

)) are expected because neighboring

terraces scatter constructively. This diﬀerence between the temporal signal

measured at in-phase vs out-of-phase conditions, is the ﬁrst experimental ev-

idence that the experiment has suﬃcient sensitivity to step ﬂuctuations and

incoherent scattering has not washed out the ﬂuctuation signal.

The relative magnitude of the expected diﬀraction ﬂuctuations δI

(0)/I

for average intensity I with M incoherent domains (for a beam of size d and

coherence length ζ, M ≈ (d/ζ)

domains) can be expressed in terms of the

relative ﬂuctuation δ

(0)/I

 within a single coherent domain [26,28] by

δI

(0)

I

=1+

I

δI

(0)

I



. (7.16)

The unity term in the right hand side is simply the known result for statistical

uncorrelated noise δ

(0)/I = 1, expected for any measurement with

average signal I. It can be shown [28] that for the case of step ﬂuctuations

the term δ

(0)/I

 canbeexpressedas

δ

(0)

(ζ/ξ)

∞

)

(1 − exp(−(ζ/ξ))) (7.17)

with all other symbols deﬁned earlier. Equations (7.16) and (7.17) indicate

the optimal conditions for the step ﬂuctuation signal to be observed. First,

although the decrease of the beam size reduces the number of incoherent

domains M and suppresses the incoherent summation, this is not necessar-

ily an advantage, as seen in (7.16), if the current density I/M remains

constant. Second, experiments on surfaces with higher vicinality (i.e. lower

L for the same w

∞

, ζ, ξ) will have larger signal in the temporal measure-

ment since k

∼ L

−3

. Such experiments demonstrating the feasibility

of temporal ﬂuctuation experiments with high resolution LEED [26], have

been ﬁrst carried out on high-index stepped W(430) surfaces in the range

T = 700–900 K by taking advantage of the improved brightness of the elec-

tron source, the high resolving power of the instrument (∆k =0.005 nm

−1

or ζ =1/∆k = 200 nm) and the high vicinality of the surface (L =7a

i. e. 7 lattice units). Fluctuations δ

(0)/I

 which increase with temper-

ature as high as up to 5 times the statistical ﬂuctuations were observed at an

out-of-phase condition k

=5π/d, while smaller ﬂuctuations, consistent with

statistical ﬂuctuations, were observed at the adjacent in-phase-condition.

Microscopic Mechanisms for Step Fluctuations

The usefulness of diﬀraction ﬂuctuation experiments can be assessed further

from the time dependence of the correlation function and the extraction of

diﬀusion barriers from the corresponding Arrhenius plots. For step ﬂuctua-

tions, the measured diﬀraction signal (which originates from phase diﬀerences

302 Michael C. Tringides and Myron Hupalo

between neighboring steps) is a collective result of the contribution of sin-

gle atom hopping events. Information about the nature of these atomistic

processes can still be extracted from the ﬂuctuation signal, because the form

of the correlation function and the measured time constants are sensitive to

the atomistic processes operating.

Three atomistic processes have been proposed in the literature to explain

how collective step ﬂuctuations are generated [31]. Each process is described

by a characteristic quantity: the step mobility Γ , the 1D diﬀusivity along the

step edge D

and θ

(the product of the equilibrium adatom concentration

and the tracer diﬀusion coeﬃcient D

since in the third process atom

detachment from the step is balanced by diﬀusion away on the terrace).

Depending on which of these three rates is the controlling one, the analysis

of step ﬂuctuations results in diﬀerent functional forms for the correlation

function. By testing which form is in agreement with the experimental data

the controlling process can be identiﬁed. In the evaporation and condensation

mechanism (EC), atom transport to other steps is controlled by Γ . It is valid

whenever Γ is suﬃciently small. Step diﬀusion (SD) applies in the opposite

limit when the detachment of atoms from the steps is fast and diﬀusion along

steps is faster than terrace transport (D

 θ

). Terrace diﬀusion (TD)

applies when Γ is very large and terrace transport is faster than step edge

diﬀusion (D

 θ

). These limits are deduced from the general expression

for the eﬀective time constant τ(k) (of a step ﬂuctuation of wavevector k

with Σ the area of an elementary hop of the diﬀusing entity) when all three

atomistic processes have comparable contributions [32]

τ(k)=

T (Γ +2θ

k + Σ

3/2

)

Γθ

βk

(2θ

k + Σ

3/2

)

. (7.18)

When one of the three limits dominates, the measurement can be analyzed

as if only one of the three processes operates; otherwise in crossover regimes

more than one process should be taken into account.

Next we outline brieﬂy the methodology of deriving the form of the cor-

relation functions for the diﬀerent atomistic processes. In general, the step

ﬂuctuation correlation function G

(t) originating from a single coherent do-

main can be written [28] in terms of the time-dependent correlation along

the step C(y, t)

(t)

I



(ς/a



)

ς/2a



−ς/2a

cosh((k



C(y, t) − 1

. (7.19)

Equation (7.19) has been derived from the summation of the amplitude

of N

independently ﬂuctuating steps in the x-direction within the coher-

ence length of the instrument ζ and the summation along the step in the

y-direction still present in (7.19). Fluctuations along the step are correlated

up to ξ(T ), i.e. essentially the distance over which C(y, t) is non-zero. ξ(T )is