Heitjans P., Karger J. (Eds.). Diffusion in Condensed Matter: Methods, Materials, Models

Подождите немного. Документ загружается.

7 Fluctuations and Growth Phenomena in Surface Diﬀusion 303

temperature dependent and is determined by the thermodynamics of the step

interactions (cf (7.15)) while ζ as a parameter of the instrument is indepen-

dent of temperature. The step can be thought of as divided into ζ/ξ separate

regions and each region contributes independently to the total ﬂuctuation

signal. The expression (7.19) is evaluated at the wavevector of maximum

sensitivity at the split spot k

= ±π/L.

The diﬀerent atomistic models diﬀer as to the functional form of the

correlation function C(y, t) or equivalently the form of its Fourier components

(t)

C(y, t)=exp(−|y|/ξa



) −

1Na



π4w



∞

−∞

(t)cos(kya



)dk. (7.20)

Expressions for C

(t) have been derived from the solution of diﬀeren-

tial equations describing the local ﬂuctuating step amplitude ∆(y,t)forthe

diﬀerent atomistic mechanisms. We have

∂∆

∂t

∂

∆

∂y

−

2Γθ

∂

∆

∂y

η(y,t)

(7.21)

where η(y,t) is uncorrelated thermal noise. As an illustration, we give the

result for the SD model. Full derivations for the other models can be found

in [28]. The solution for the Fourier coeﬃcients of the correlation function

C(y, t)is

(t)=ξ

(1 − exp(−(t/τ

)(a/ξ)

{(ξk)

+(ξk)

}))

(ξk)

. (7.22)

All symbols in (7.22) have been deﬁned before except τ

,whichisthe

characteristic time for the rate controlling atomic event, i. e. the time for the

diﬀusing entity (i. e. atom, dimer, etc.) to hop a distance Σ

0.5

along the step

edge i. e. τ

≈ Σ/2D

From (7.22) one can derive the correlation function C(y, t)bymeansof

(7.20), the expected expression G

(t) for the single-domain (7.19) at an out-

of-phase condition k

=(2l +1)π/d, and ﬁnally the expression for the mea-

sured correlation function (7.16) which includes the eﬀect of the incoherent

summation over the beam size.

It has been shown in [28] that the expression for G

(t)attimest>τ

1/2

(where τ

1/2

is the time for the correlation function to drop to half its initial

value, G

(τ

1/2

)=G

(0)/2)) can be written in the general form

(t)=G

(0) exp



−A(n)(t/τ

)

1/n

(7.23)

with the exponent n diﬀerent for the three atomistic models, n =1forEC,

n =3forTDandn = 4 for SD kinetics. Equally important is the determina-

tion of the energetic barriers of the atomistic process, from the temperature

304 Michael C. Tringides and Myron Hupalo

dependence of the time constant τ

1/2

(T ) of the correlation function. The

connection between τ

1/2

(T ) and the microscopic time τ

of the individual

atomistic event is diﬀerent for each of the three cases and is made through

the model-dependent parameter A(n)via



A(n)

0.693



1/2

. (7.24)

For example, for the speciﬁc SD model already discussed in (7.21) and (7.22)

we have

A(n =4)=(0.74)





(2θ

Ω

3/2

)/k

T. (7.25)

Thermal Fluctuations on Stepped Si(100)

with High Resolution LEED

These theoretical predictions have been tested in high resolution LEED ex-

periments [27] on vicinal Si(100) crystals of misorientation ∼ 1

◦

(i.e. the

average terrace is L =6.5 nm). 200 independent samples were averaged

to minimize statistical noise. The experiment was performed in the range

950 K <T <1130 K. Fitting the static proﬁles along the step I(k

)wasused

to deduce the correlation length ξ(T ) and to extract the step stiﬀness

β from

(7.15) (

β in turn can be used to deduce the kink and corner step energies

within the terrace-step-kink TSK model [27]) and the step-step interaction

“force constant” c = ∂

U/∂x

. It is possible to deduce two independent pa-

rameters,

β(T )andc, from a single measured one (ξ(T )), because ξ(T )can

be uniquely written as the sum of a term varying strongly with temperature

and another term practically temperature independent. As seen from (7.15)

these components correspond to

β and c, respectively.

Time-dependent correlation functions are shown in Fig. 7.5(a) for the two

extreme temperatures 948 K and 1123 K. Both G(0) and τ

1/2

(T ) follow the

expected temperature dependence described earlier: G(0) being proportional

to w

∞

(where w

∞

is the mean square deviation of the step) increases with

T ,andτ

1/2

(T ), the time constant of the ﬂuctuations, decreases with T .The

value of G(0)/I = δ

I(0)/I is equal to 4 ×10

−3

and still small with re-

spect to the value 1 of statistical noise at t = 0. However, averaging over 200

independent samples reduces statistical noise for ﬁnite times t>0sothat

the correlation function is observed above the noise. Figure 7.5(b) shows a

ﬁt of the time dependence of the form of the correlation function accord-

ing to (7.23). Exponential decay (i.e. n = 1) is ruled out by the ﬁt so EC

is not the operating mechanism. The data are compatible with n =4(SD

mechanism) and with n = 3 (TD). The test of the functional form of G(t)is

therefore not suﬃcient to distinguish between these two possibilities. Ener-

getic considerations of the extracted diﬀusion barriers, to be discussed next,

favor n =4.

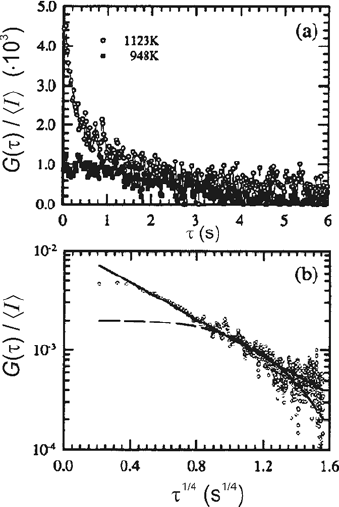
7 Fluctuations and Growth Phenomena in Surface Diﬀusion 305

Fig. 7.5. (a) High-resolution

LEED correlation function on

stepped Si(100) at two tempera-

tures. (b) The ﬁts of the time de-

pendence of the correlation func-

tion exclude exponential decay

and therefore rule out the EC

model for step ﬂuctuations.

From the temperature dependent data the decay times τ

1/2

(T )areex-

tracted for each correlation function with the two compatible ﬁts (n =3or

4). The τ

1/2

values clearly do not depend on n, however the atomistic times

which correspond to the single atomistic events generating the ﬂuctuations

(and therefore the microscopic barriers) do, through (7.24), (7.25). For SD

kinetics we measure the step edge diﬀusion barrier E

=0.8 ±0.2eV and the

prefactor ν

=10

10±2

−1

, while for the TD case we measure E

=1±0.2eV

and ν

=3× 10

8±2

−1

. In TD kinetics two activated barriers are involved

additively in the ﬁnal activation energy, i.e. the barrier controlling the equi-

librium coverage θ

of the detached entity (i.e. the dimer formation energy

for Si(100)) and the terrace diﬀusion barrier E

. The extracted activation

energy from the ﬂuctuation experiments should be the sum E

= E

.As

discussed in [27], from other experiments E

=0.67 eV is known and theo-

retical estimates give E

=1.6 eV, so the measured activation energy of 1 eV

(if n = 3 is assumed) is too low to be consistent with these independently

known energies. The data suggest that SD and n = 4 is the most probable

microscopic mechanism.

Step ﬂuctuations of Si(100) have been studied before with low energy

electron microscopy (LEEM), both at equilibrium [31] (by analyzing real-

space LEEM images of ﬂuctuating steps with video acquisition speed and

at length scales ≈ 10 times the LEED coherence length ζ) and during non-

306 Michael C. Tringides and Myron Hupalo

equilibrium ripening experiments [35] (by monitoring after Si deposition, how

the nucleated islands grow in time). Because the LEEM experiments follow

the evolution of the system over larger length scales higher temperatures

were used (T>1090 K) than in the diﬀraction experiments. From the LEEM

studies it was deduced that the microscopic mechanism responsible for the

step ﬂuctuations is not SD, as in the diﬀraction experiment, but EC. This

conclusion was based on the wavevector dependence of the time constants

(τ(k) ∼ k

) deduced from the relaxation of the Fourier components C

(t)

of the correlation function calculated from time-dependent LEEM images.

It was further supported from the linear dependence of the growing island

area (A ∼ t) in the non-equilibrium ripening experiments [35]. This raises

the interesting question why the diﬀraction experiments indicate that SD is

most probably the microscopic mechanism operating and not EC kinetics.

As mentioned before in discussing (7.18) all atomistic mechanisms operate

simultaneously and one can identify a single mechanism responsible for the

ﬂuctuations only when the inequalities between the atomistic rates Γ , θ

described in Sect. 7.3.1 (p. 302) are strictly obeyed. However, as seen in

(7.18), the limiting values, where a single atomistic process is the dominant

one, are strong functions of the temperature and the length scale of the exper-

iment (i.e. the inverse of the probing wavevector of the technique k

−1

). From

(7.18) it is seen that the various limits between Γ , θ

, D

depend both

on T (since in principle diﬀerent activation energies and prefactors describe

the diﬀerent rates) and the wavevector k. Since in LEEM both the tempera-

ture range is higher (by approximately 300 K) and the probing wavevector is

smaller by a factor of 10 than in the diﬀraction experiment, the EC process

is weighted more, but at lower temperatures or larger k the SD process is

favored. The main conclusion from this comparison is that although it is not

appropriate to assign a single atomistic process, the comparison of diﬀerent

experiments is legitimate, in terms of the Arrhenius parameters (i.e. activa-

tion energies and prefactors). The Arrhenius parameters are independent of

which atomistic process operates in a given temperature range.

7.3.2 STM Tunneling Current Fluctuations

Correlation Functions in Probe Area STM Experiments

The use of STM to study ﬁnite coverage diﬀusion and the role of interactions

has been demonstrated in [33, 34] by measuring the mean residence time of

an adatom as a function of adatom separation. Such FIM-like experiments

require a large number of statistics. No time-dependent correlation functions

were measured. As shown by (7.8), equilibrium diﬀusion measurements can

be carried out by analysing the decay of the autocorrelation of concentration

ﬂuctuations within a probe area A. In such experiments the possibility of

measuring ﬂuctuations at selective wavevectors is lost, since the measured

signal integrates the total number of adatoms within A. An area is naturally

7 Fluctuations and Growth Phenomena in Surface Diﬀusion 307

deﬁned in the STM geometry because the tunneling current depends expo-

nentially on the tip-surface separation and most of the current is conﬁned

within a narrow cone with its apex at the tip.

If the surface coverage θ is constant, the number of adatoms in A, N (t),

will ﬂuctuate around its average value

N = Aθ as adatoms diﬀuse in and out

of the area. The tunneling current i(t) depends on the tip-surface separation

z and the electronic structure within A (i. e. the local “workfunction” ∆ϕ)

which is determined by the number of adatoms within A. I(t) is uniquely

determined by N(t) at a given time, since both z and ∆ϕ are functions

of N(t). As N(t) changes, its ﬂuctuations δN(t)=N(t) −

N will produce

ﬂuctuations in the tunneling current ∆i(t)=i(t) −

i with i denoting the

average tunneling current. The time dependence of the current ﬂuctuations

∆i(t) will follow the time dependence of ∆N(t) and hence the ﬂuctuations due

to the adatom diﬀusion in and out of A. Equation (7.8) can be measured from

the tunneling current autocorrelation function for suﬃciently small ∆N/

N 

∆N(t)∆N(0) = γ

∆i(t)∆(0) = γ

k=N



k=1



i(t

+ t) − i



i(t

) − i



(7.26)

where γ is a proportionality constant relating ∆i(t)to∆N (t). For systems

with no interactions and for any size A (even as small as one unit cell) it has

been shown by Monte Carlo simulations [36] that the functional form of (7.8)

is given by

∆N(t)∆N(0) = δN

(0)



−r

/4Dt

4πD

r (7.27)

which is simply the probability for an initial ﬂuctuation of strength δN

(0)

to remain within A after time t. Equivalently, if the power spectrum W (ω)

is measured, instead of the correlation function, it is given by the Fourier

transform of (7.27),

W (ω)=



∆N(t)∆N(0)e

iωt

dt. (7.28)

The experimental situation is shown schematically in Fig. 7.6. The decay of

the correlation function in the short-time limit is approximately exponential

(equivalently (7.28) follows the Lorentzian ω

−2

dependence in frequency).

In the long-time or zero-frequency limit, the correlation function has the

characteristic 1/D

t tail, typical of diﬀusion in two dimensions. Equivalently,

W (ω) has the form

W (ω)=

δN

(0)A ln ω

4πD

for ω → 0 . (7.29)

Preliminary experiments [23] on O/Si(111) have shown that such STM

ﬂuctuation measurements are possible. The evidence was based on the much

308 Michael C. Tringides and Myron Hupalo

Fig. 7.6. Schematic presenta-

tion of the STM ﬂuctuation ex-

periment where either the time

dependent correlation (left) or,

equivalently, the power spectrum

(right) of the tunneling current I

vs time t canbeusedtomeasure

the diﬀusion coeﬃcient.

higher ﬂuctuation level ∆i

(0)

0.5

/i for the adsorbate covered vs clean sur-

face, on ﬁtting the measured spectra to the characteristic ln ω dependence on

ω as in (7.29) and to the Arrhenius dependence of the time constants τ(T )vs

1/T in the range T = 400–550 K to extract an activation energy of diﬀusion

E = 1 eV. However, the O/Si(111) system is highly complex with adsorbed

oxygen in diﬀerent bonding conﬁgurations [37], so it is diﬃcult to interpret

the extracted value of E in terms of the energetic barrier of a single diﬀusing

species.

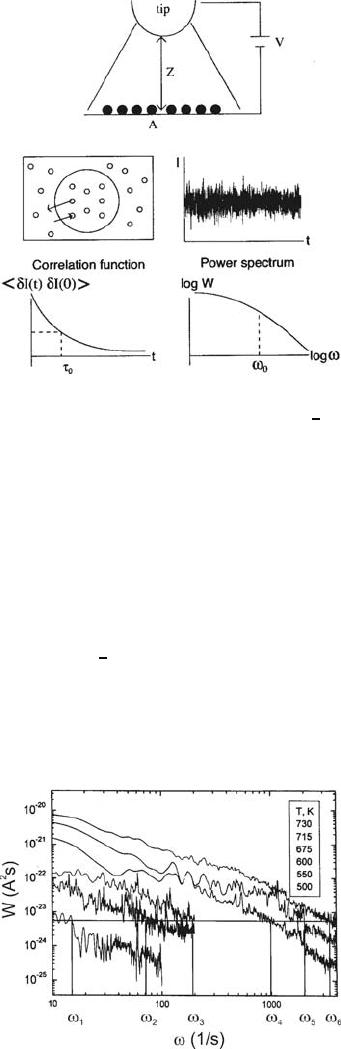
Figure 7.7 presents power spectra obtained for the H/Si(111) system at

saturation coverage, θ → 1, in the range T = 500–730 K. The tunneling con-

ditions are

i =1nAandV = −15 V (tunneling from the sample to the tip)

which corresponds to a tip-surface separation of ≈ 3 nm. The separation is

measured experimentally by modulating the position of the z-piezo ∆z and

detecting the corresponding current component ∆I with a lock-in ampliﬁer.

Fig. 7.7. Power spectra for

H/Si(111) close to saturation

(θ → 1) as a function of temper-

ature (T = 500–730 K) showing

that the mean square ﬂuctua-

tions δN

(0) increase while the

spectral content shifts to higher

frequencies with increasing tem-

perature.

7 Fluctuations and Growth Phenomena in Surface Diﬀusion 309

∆ log I/∆z corresponds to the tunneling barrier. The point where the barrier

“collapses” is identiﬁed as the contact point between tip and surface. Once

this point is identiﬁed, the tip-surface separation is determined by the diﬀer-

ence in the z-piezo voltages between the “contact” voltage and the voltage

of interest.

The spectra include higher frequencies outside the low frequency limit

of (7.29), so the ﬁtting requires the full expression (7.28). The spectra are

consistent with H diﬀusion as seen from the increase of the integrated area

under the curves (which is a measure of ∆N

(0)) and the shift of the

spectral content to higher frequencies with increasing temperature. The time

constants τ(T ) are obtained by ﬁtting the spectra to (7.27), (7.28) and, when

plotted in Arrhenius form, an activation energy E =1.3 eV is extracted, in

good agreement with earlier optical grating measurements on H/Si(111) [38]

over mesoscopic length scales.

For measuring only the diﬀusion activation energy, it is suﬃcient to ob-

tain the ratios of the time constants at diﬀerent temperatures τ(T

)/τ(T

However, full information about surface diﬀusion requires two additional is-

sues to be addressed. First, it is important to deduce the absolute value of D

(i.e. in addition to E) to be able to extract the diﬀusion prefactor. Second,

it is not clear whether the form of the correlation function (cf (7.27)) is true

in systems with interactions (i. e. it is an open question whether in the limit

t →∞the correlation function follows the 1/D

t dependence), especially at

low temperatures when ordered phases are present. Although changes in the

form of the correlation function do not aﬀect the extracted value of E,they

can indicate diﬀerent cooperative dynamics (i.e. critical slowing down close

to a second-order phase transition).

Tunneling Area Determination from STM Fluctuations

We can answer the ﬁrst question if the size of the tunneling area A can be

measured. In principle, the area can be estimated from a solution of the

Schroedinger equation to match the measured tunneling current i(V )ata

given voltage V . The accuracy of the estimate depends on the sophistication

of the model of the tunneling process and unknown experimental parame-

ters like tip shape and sharpness. Because of these caveats, we suggest an

experimental method to measure the tunneling area which is based on only

measurable quantities.

The tunneling area is expected to increase monotonically with the tip-

surface separation z. The tunneling current i(z,N) for a ﬁxed voltage V is a

function also of N where N is the number of adatoms within the tunneling

area since the local “workfunction” ∆ϕ is determined by N . For a change

∆N (and ﬁxed z), we can write the corresponding tunneling current change

as a result of an equivalent change of z

∆i =

∆i

∆z

∆N

· ∆N (7.30)

310 Michael C. Tringides and Myron Hupalo

or for the relative current change

∆i

∆ log i

∆z

∆N

· ∆N . (7.31)

This assumption is justiﬁed since ∆ log i/∆z is the eﬀective barrier in the

tunneling process with

N adatoms in A. ∆ log i/∆z is uniquely deﬁned be-

cause

N is approximately constant (when ∆N/N  1 is satisﬁed) and the

geometry of the two electrodes (i.e. “conically”-shaped tip and planar surface)

remains unchanged.

In the limit of θ → 1 diﬀusion is caused by the motion of a small number

of vacancies (θ

≈ (1 − θ)), so the problem can be analyzed by considering

a dilute gas of N

vacancies. When N

→ 0, the relative ﬂuctuation (using

the compressibility of a Langmuir gas) can be approximated as ∆N

max

(1 − θ)

θ)

0.5

max

(1 − θ)

∼

= N

−1/2

max

, i. e. it is the inverse of the square

root of the number of sites in the tunneling area.

The N

vacancies are generated in the adatom layer of thickness z

(where

is the apparent height of a single adatom). The rate of change ∆z/∆N for

N close to N

max

canbewrittenasz

max

since the motion of one atom into

or out of A causes on the average only 1/N

max

fractional change of z

, (i.e.

is the change of the tip-surface separation when all atoms are removed).

We can rewrite (7.31) in terms of the unknown quantity N

max

,whichis

the number of sites within A,

max



(∆ log i/∆z)z

/∆i/i



. (7.32)

All three quantities on the right hand side of (7.32) can be measured

experimentally: ∆i/

i is the ratio of the mean square ﬂuctuation to the average

current (or, equivalently, the area under the power spectrum W (ω)) to

i),

∆ log i/∆z is the eﬀective barrier height, measured with the lock-in technique

described before and z

(= 0.1 nm) is obtained from the apparent atom height

in STM images.

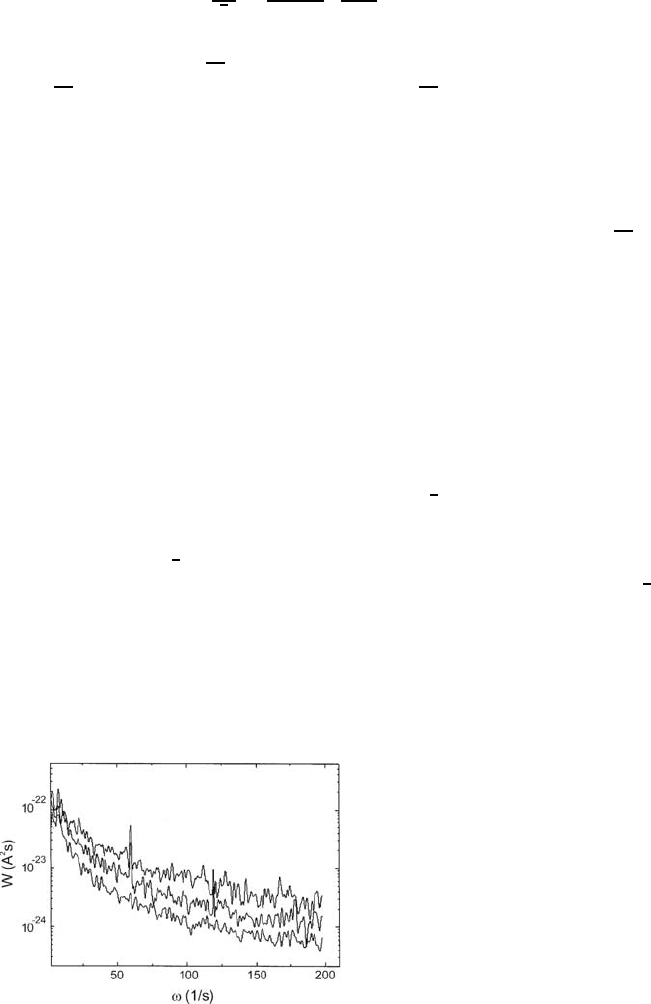
Figure 7.8 shows such power spectra at three tip-surface separations on

H/Si(111) at θ → 1 in the frequency range 0–200 Hz and T = 600 K [22].

Fig. 7.8. Power spectra for

H/Si(111) close to θ → 1asa

function of the tip surface sepa-

ration z showing that the lower

spectrum (V = −15 V and larger

tip-surface separation z ≈ 3nm)

has spectral content shifted to

lower frequencies because of the

larger tunneling area.

7 Fluctuations and Growth Phenomena in Surface Diﬀusion 311

In the spectra of Fig. 7.8 the tunneling current is ﬁxed (I = 1 nA) and

the tip-surface separation is varied from 0.4 nm to 3 nm by varying V (z is

measured from the point of “collapse” of the barrier ∆ log I/∆z ≈ 0and

the change of the voltage on the z-piezo). The spectra for the larger voltage

V = −15 V (i.e. larger tip-surface separation z =3nm)havemorespectral

weight to lower frequencies, as expected for larger tunneling area. By using

the measured values V = −15 V, ∆ log I/∆z =2.5nm

−1

, ∆i/i =0.038,

=0.1nm we obtain N

max

= 43 hydrogen binding sites. If we assume

that each site corresponds to a Si(1 × 1) unit cell this amounts to an area

A =4.5nm

which is used to deduce a prefactor D

=1.5 ×10

−7

/s in the

experiments of Fig. 7.7.

Correlation Functions in Interactive Systems

We return to the second question raised previously, viz what is the shape of

the correlation function ∆N(t)∆N(0) if there are interactions between the

adatoms. Such questions have been addressed with mean ﬁeld theory [39] and

Monte Carlo simulations in model systems [36], with the results of the two

methods being in good agreement with each other.

An Ising model with repulsive interactions was used for illustration. At low

temperatures the ordered c(2 × 2) phase forms. The most demanding condi-

tion for determining whether ∆N(t)∆N(0) follows the non-interactive (i. e.

site exclusion) expression (7.27) is for the smallest probe area A because in

this case the most pronounced deviations from the long-wavelength “hydro-

dynamic” regime are present. For this reason, in [36] the single-site correlation

function (i.e. the probe area side is one lattice constant) was used. As stated

before for the case of site-exclusion, even for such small areas ∆N (t)∆N(0)

obeys (7.27) and has the characteristic 1/D

t tail. This is not surprising

since the evolution of the step concentration proﬁle for site exclusion (which

also includes short-wavelength components) follows (7.9). i. e. the solution for

non-interactive systems.

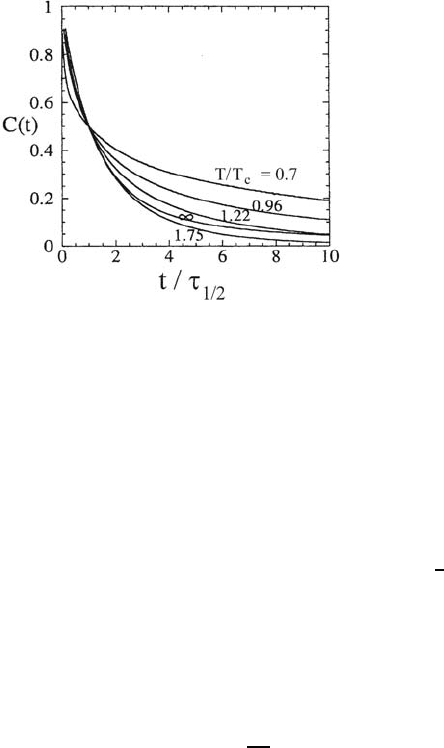
Figure 7.9 shows results for the single-site correlation function obtained

in [36] as a function of T/T

. The results are plotted in terms of the scaled

variable t/τ

1/2

(where τ

1/2

is the time for the correlation function to drop

to 1/2 of its initial value) to check for deviations from the non-interactive

form obtained for T/T

→∞. Deviations are seen at lower temperatures

and the characteristic 1/D

t tail is not observed for intensity levels as low as

−3

of the initial value of the correlation function at t =0.Itisnotknown

whether the tail will be seen for lower values of the correlation function,

although such values are below the detectability limit of current ﬂuctuation

experiments. Deviations of the correlation function from the non-interactive

form (cf (7.27)), are also expected for larger probe areas, but the degree of

deviation should be less. It is an open question to determine these deviations

in other lattice gas models with diﬀerent types of interactions.

312 Michael C. Tringides and Myron Hupalo

Fig. 7.9. Single-site (i.e. probe

area is 1×1 cell) correlation func-

tions as a function of the scaled

variable t/τ

1/2

in an Ising model

with repulsive interaction θ =

0.5 calculated with Monte Carlo

simulations. The results show

that for temperatures within the

orderedregion(T/T

< 1) there

are deviations from the non-

interactive (T/T

= ∞)formof

the correlation function.

The high electric ﬁeld E(r) present in STM experiments raises the ques-

tion whether the ﬁeld can aﬀect the measurements by changing diﬀusion,

from purely random to a biased random walk [40]. The magnitude of the

eﬀect will depend on the type of the adsorbed atom. Larger eﬀects should

be expected for adatoms which have non-zero dipole moments. For adatoms

with zero dipole moments the eﬀect should be smaller and should depend on

the adatom polarizability. We examine this latter case in detail because it is

applicable to the two ﬂuctuation experiments described earlier, i. e. H/Si(111)

and O/Si(111). The electrostatic energy between an adatom with polarizibil-

ity α in an electric ﬁeld E(r)isgivenbyU

(r)=

αE

(r). Since the energy

does not depend on the sign of the electric ﬁeld, similar eﬀects should be

expected independent of the voltage polarity. The energy U

will be lower

where E(r) is strongest (i. e. underneath the tip), so the diﬀusing atoms will

move towards the tunneling area. The ratio of the probability to diﬀuse to-

wards (P

↑

) over the probability to diﬀuse away (P

↓

) from the tunneling area

is given by

↑

↓

(r)/k

. (7.33)

Since the electric ﬁeld falls with the distance r from the tunneling area with

a power law dependence, this biased diﬀusion will extend over long distances.

The role of the ﬁeld on diﬀusion is based on two eﬀects. First, diﬀusion in

this “tilted” potential energy surface will have the eﬀect of rearranging the

atom distribution (if initially the atoms are deposited randomly on the sur-

face) to one with maximum coverage within the tunneling area underneath

the tip. This eﬀect has been observed in the H-on-Si(111) system, when af-

ter randomly depositing θ<0.05 ML, a circular region of higher coverage

(θ ≈ 0.25 ML, i. e. ﬁve times the initial θ) is seen underneath the tip if the

tunneling voltage 6 V is kept on for 1/2 hour [22]. Second, the shape of the

correlation function can deviate from the non-interactive shape (cf (7.27))