Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


26,
----'-
_
Analysis
of
Tensors
Tensor algebra deals with lifeless vectors and tensors--objects that do not move,
do not change, possess no dynamics. Whenever there is a need for tensors in
physics, there is also a need
to know the way these tensors change with position
and time. Tensors that depend on position and time are called tensor fields and are
the snbject of this chapter.
Instndying the algebra
of
tensors, we leamed that they are generalizations of
vectors. Once we have a vector space V and its dual space V*, we can take the
tensor products of factors
of
V and V* and create tensors
of
various kinds. Thus,
oncewe knowwhatavectoris, we canmakeup
tensors
from
it.
In the
previous
chapter,
we didnot
concern
ourselves withwhatavector
was;
we simply assumed that it existed. Because all the vectors considered there were
stationary,
their
mere
existencewas
enough.
However,
in
tensor
analysis,
where
things keep changing from point to point (and over time), the existence of vectors
atone pointdoesnot
guarantee
their
existenceat all
points.
Therefore,
we now
have to demand more from vectors than their mere existence. Tied to the concept
of
vectors is the notion of space, or space-time.
Let
us consider this first.
26.1 Differentiable Manifolds
Space is one
of
the undefinables in elementary physics. Length and time intervals
are concepts that are
"God
given," and any definitions of these concepts will be
circular. This is true as long as we are confined within a single space. In classical
physics, this space isthe three-dimensionalEuclideanspace in which every motion
takes place. In specialrelativity, space is changedto Minkowskispace-time.
Innon-
relativistic quantum mechanics, the underlying space is the (infinite-dimensional)
Hilbert space, and time is the only dynamical parameter. In the general theory

764 26.
ANALYSIS
OF
TENSORS
of
relativity, gravitation and space-time are intertwined through the concept
of
curvature.
Mathematicians have invented a unifying theme that brings the common fea-
tures
of
all spaces together. This unifying theme is the theory
of
differentiable
manifolds. A rigorous understanding
of
differentiable manifolds is beyond the
scope
of
this book. However, a working koowledge
of
manifold theory is surpris-
ingly simple.
Let
us begin with a crude definition
of
a differentiable manifold.
differentiable
manifold
provisionaily
defined
coordinate
functions
andcharts
eOO-related
charts
andatlases
26.1.1. Definition.
A differentiable
manifold
is a collection
of
objects called
pointsthat are connectedto each other in a smoothfashionsuch that the neighbor-
hood
of
each point looks like the neighborhood
of
an m-dimensional (Cartesian)
space; m
is called the dimension
of
the manifold.
As is customary in the literature, we use "manifold" to mean "differentiable
manifold."
26,1.2.
Example.
The following are examplesof differentiable manifolds.
(a) The space
R"
is an a-dimensional manifold.
(b) The surface of a sphere is a two-dimensional manifold.
(c)
A torus is a two-dimensional manifold.
(d)
The
collection
of
all n x n
real
matrices
whose
elements are
real
functions having
derivatives
of
all orders is an n
2-dimensional
manifold.
Here
a
point
is an n x n matrix.
(e)Thecollectionof allrotationsin
1R
3
is a three-dimensional manifold. (Hereapointis a
rotation.)
(f) Any smooth surface in]R3 is a two-dimensional manifold.
(g) The unit n-sphere
Sn,
which
is the collection
of
points in lR
n
+I satisfying
2 2 I
Xl +---+X
n
+
l
= ,
is a manifold.
Any surface with sharp kinks, edges, or points cannot be a manifold. Thus, neither
a cone nor a finite cylinder is a two-dimensional manifold. However, an infinitely long
cylinder
is a manifold.
III
Let
Up denote a neighborhood
of
P.
When
we say that this neighborhood
looks like an m-dimensional Cartesian space, we
mean
that thereexists a bijective
map
rp
: Up
->
IR
m
from a neighborhood Up
of
P 10 a neighborhood rp(Up)
of rp(P) in IR
m
,
such that as we move the
point
P continuously in Up, its image
moves
continuously in rp(Up). Since rp(P) E
IRm,
we
can
define functions xi :
Up
->
IR such that rp(P) =
(x1(P),
x
2(P),
...
,
xm(P».
These functions are
called
coordinate
functions
of
tp,
The
numbers xi
(P)
are called
coordinates
of
P.
The
neighborhood Up together with its mapping
rp
fomn a
chart,
denoted by
(Up,rp).
Now
let (Vp,
1-')
be another chart at P with coordinate functions I-'(P) =
(yl(p),
y2(p),
...
,ym(p»
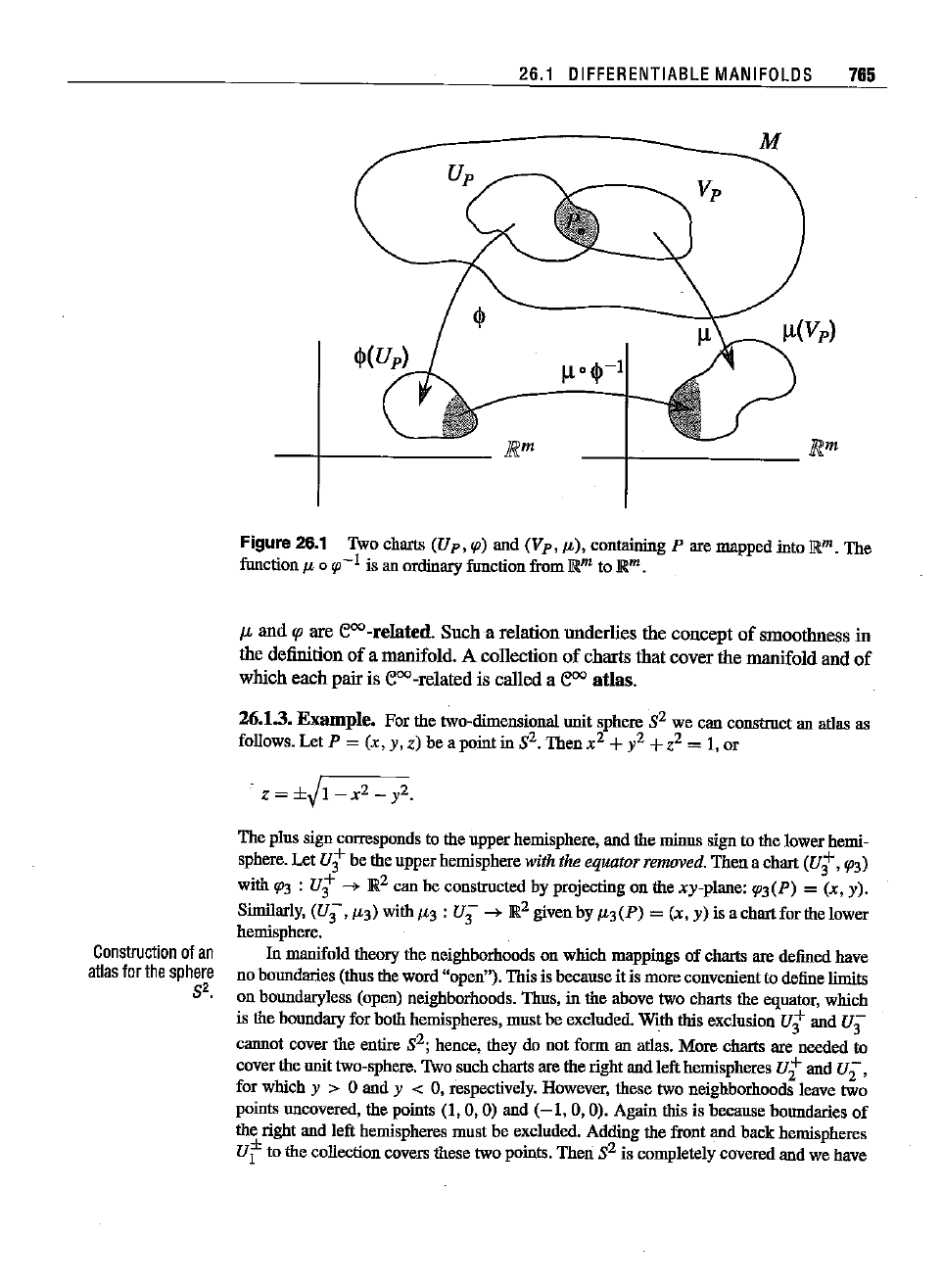
(see Figure 26.1).
It
is assumed that the function
I-' 0 rp-l : rp(Up nV
p)
->
I-'(Up nV
p),
which maps a subsel
of
IR
m
to another
subset
of
IR
m
, possesses derivatives
of
all orders. Then, we say that the two charts
26.1
DIFFERENTIABLE
MANIFOLDS
765
_-----
__
M
_-+
Jlf.m
Figure 26.1 1\vo charts
(Up,
'fJ)
and
(Vp,
JL),containing P are mapped into
Ill.m.
The
function
JL
0
cp
-1
is an
ordinary
functionfromIRm to
JRm.
f-L
and
'fJ
are e
oo
-related. Such a relation underlies the concept
of
smoothness iu
the definition of a manifold. A collection
of
charts that cover the manifold and
of
which each pairis e
oo
-related is called a
e
oo
atlas.
26.1.3.Example. For the two-dimensional unit sphere S2 we can construct an atlas as
follows. Let
P =(x, y, z) be a point in S2. Then x
2
+ y2 +z2 = I, or
Construction
of
an
atlas
for
the
sphere
S'.
Theplus sign
corresponds
to theupperhemisphere, andtheminussigntothelowerhemi-
sphere. Let
ut
be the upperhemisphere with the equator removed.Thena chart
(ut,
'fJ3)
with
'fJ3
:
ut
.....
]R2
can be constructed by projecting on the xy-plane: 'fJ3(P) = (x, y).
Similarly,
(U;,
JL3)
with
JL3
:
U;
.....
]R2
given by JL3(P) = (x, y) is a chart for the lower
hemisphere.
In manifold theory the neighborhoods on which mappings
of
charts are defined have
no
boundaries
(thus
the
word
"open").
Thisis becauseitis moreconvenient todefine
limits
on
boundaryless
(open)
neighborhoods. Thus,in the abovetwo
charts
the
equator,
which
is the
boundary
forbothhemispheres, mustbeexcluded.Withthisexclusion
Ui
andUi
cannotcoverthe
entire
S2; hence, they do not forman
atlas.
More
charts
areneededto
covertheunit
two-sphere.
1\\'0 such
charts
aretherightandlefthemispheres
ut
and
U2',
forwhich y > 0 andy <
O.
respectively.
However,
these twoneighborhoods leavetwo
points uncovered, the points
(1,0,0)
and
(-I,
0, 0). Again this is because boundaries
of
therightandleft
hemispheres
mustbe excluded. Addingthe frontandbackhemispheres
ut
to thecollectioncoversthesetwopoints.ThenS2 is completelycoveredandwe have

766 26. ANALYSIS
OF
TENSORS
anatlas.Thereis, ofcourse,a lotofoverlapamongcharts.Wenowshowthattheseoverlaps
are e
oo
-related.
Asan illustration, we consider the overlap between
ut
and
Ui.
This is the upper-right
quarter of the sphere. Let
(Ui,
1'3) aud
(Ui,
'fJ2)
be charts with
qJ3(x,
y, z) = (x, y),
qJ2(X,
y, z) = (x, z}.
The inverses are therefore given by
1'3
1
(x, y) = (x, y, z) = (x, y,
Jt
- x
2
- y2),
1',1
(x, z) = (x, y, z) = (x,
~t
- x
2
- z2, z),
aud
1'20
1'3
1
(x, y) =
qJ2(x,
y,
JI-x
2
- y2) = (x,
JI-x2
_ y2).
Let us denote
CfJ2
0
qJ3
1
by
F,
so that F :
JR2
--+
]R2
is descnbed by two functions, the
components
of
F:
Fl(X,
y) = x aud
,
illustration
of
stereographic
projection
The first component has derivatives
of
all orders at all points. The second component has
derivatives of all orders at all points except at x
2
+y2 = 1, which is excluded from the
region
of
overlap
of
ut
and
vt,
for
which
z can
never
be zero. Thus, F has derivatives
of
all orders at all points
of
its domain
of
definition.
One
can similarly show that all regions
of
overlap for all charts have this property, i.e.,
all charts are e
oo
-related.
IIIlI
26.1.4. Example. For 8
2
of the preceding example, we cau find a new atlas in terms
of new coordinate functions. Since
X[
+
xI
+
x~
= I, we can use spherical coordinates
e=
cos-
1
x3,
I'
=tau-I(X2/Xl). A chart is theu given by (8
2
- {I} -
(-I),
J1.),
where
Jk(P) = (8,
rp)
maps a point of 8
2
onto a region in
IR2.
This is 'schematically shown in
Figure 26.2. The singletons {I} aud
{-I}
are the north aud the south poles, respectively.
This chart cannot cover
all of 8
2,
however, because when e=0 (or
:n'),
the value of the
azimuthal angle
rp
is not determined. In other words, e = 0 (or :n') determines one point
of the sphere (the north pole or the south pole), but its image in
IR
2
is the whole range of
q;
values. Therefore, we must exclude e= 0 (or rr) from the chart (8
2,
Jk).To cover these
two points, we need more charts.
IIIlI
26.1.5. Example. Athird atlas for 8
2
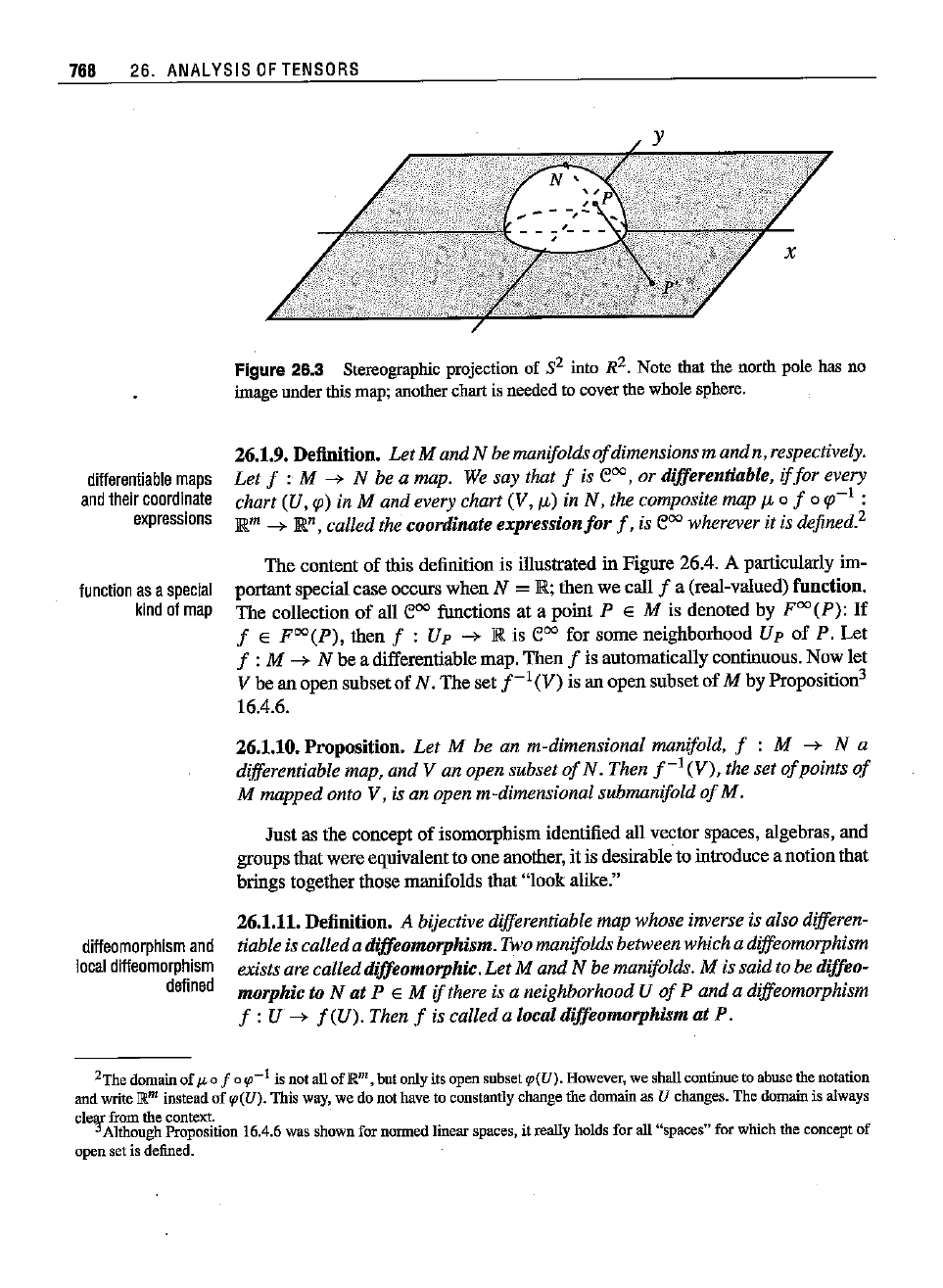
is the so-called stereographic projection shown
in Figure 26.3. In such a mapping the image of a point is obtained by drawing a line from
the north pole to that point
andextending it, if necessary, until it intersects the Xlxz-plane.
It
cau be verified that the mapping
I'
: 8
2
- {I}
-+
]R2
is given by
I'
(xtoX2,x3) =
(~,~).
I-X3
1-
X3
We see that this mapping fails for X3 = I, that is, thenorth pole. Therefore, the north
pole must be excluded (thus, the domain 8
2
- {Ij). To cover
the
north pole we need
another stereographic
projection-this
timefrom the south pole. Then the two mappings
will cover all of 8
2,
and it can be shown that the two charts are
e
oo
-related (see Example
~I.I~
•
26.1
DIFFERENTIABLE
MANIFOLDS
767
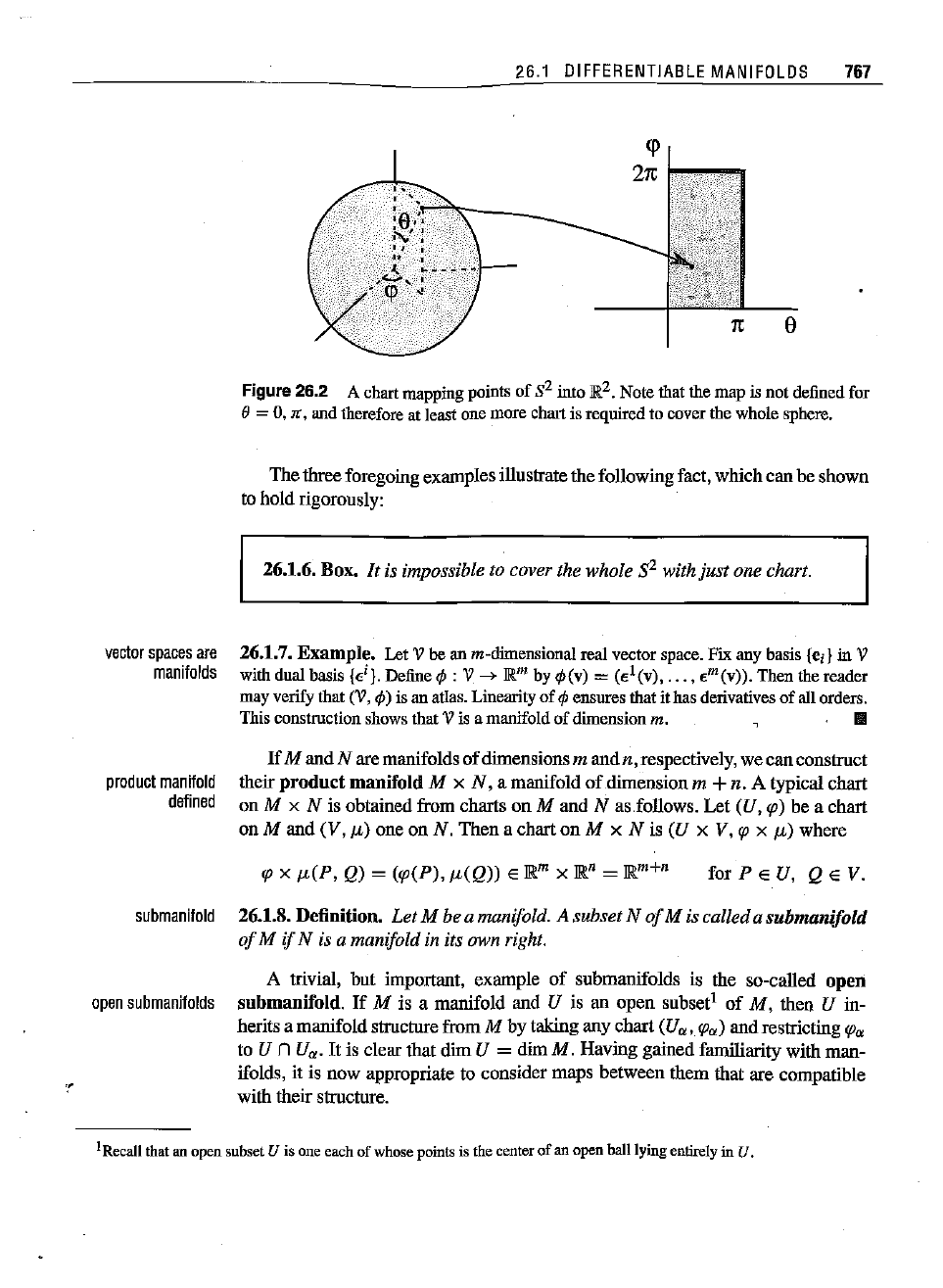
Figure
26.2 A chart mapping points
of
S2
into
}R2.
Note
that the
map
is
not
defined for
f) = 0, 1C, and therefore at least one
more
chart is required to cover the whole sphere.
The threeforegoing examples illustratethe following fact, whichcan he showu
to hold rigorously:
26.1.6. Box.
It
is impossible to cover the whole
S2
with
just
one chart.
vector
spaces
are
manifolds
product
manifold
defined
26.1.7. Example. Let Vbean m-dirnensional real vector space. Fix any basis
{es
I in V
withdualbasis [e'}. Define
</>
: V -e-
~"'
by
</>(v)
=
(el(v),
...
,
e"'(v».
Thenthereader
may verify that
('\7,
tP)
is an atlas. Linearity
of
¢ ensures that it has derivatives
of
all orders.
Thisconstruction showsthat Vis a manifold of dimension m.
11II
If
M and N are manifolds
of
dimensionsm and n, respectively, we can construct
their
product
manifold M x
N,
a manifold
of
dimension m +n. A typical chart
on
M x N is obtained from charts on M and N as.follows, Let (U, ",) be a chart
on
M and (V,
",)
one on N. Then a char1on M x N is (U x V, '" x ",) where
'"
x
",(P,
Q) =
(",(P),
",(Q» E jR"' x jRn = jR",+n
for P E U, Q E V.
submanifold
26.1.8. Defiuition. Let M be a manifold. A subsetN
of
M is calleda submanifold
of
M
if
N is a manifold in its own right.
A trivial, but important, example
of
submanifolds is the so-called
open
open
sub
manifolds
submanifold.
If
M is a manifold and U is an open subset!
of
M,
then U in-
herits a manifoldstructmefrnm
M by taking any chart
(U.,
"'.)
and restricting
"'.
to U n Ua-
It
is clear that dim U = dim M. Having gained familiarity with man-
ifolds, it is now appropriate to consider maps between them that are compatible
with their structme.
IRecall that an open subset U is one each
of
whose points is the center
of
an open ball lying entirelyin U.
768 26. ANALYSIS
OF
TENSORS
Figure 26.3
Stereographic
projection
of S2 into R
2.
Note
thatthe
north
potehasno
image under this map; another chart is needed to cover the whole sphere.
differentiable
maps
and
their
coordinate
expressions
function
asa
special
kind
of
map
diffeomorphism
and
local
diffeomorphism
defined
26.1.9.Definition. Let M and N be manifolds
of
dimensions m
and
n, respectively.
Let f : M
~
N be a map. We say that f is e
oo
, or differentiable,
if
for every
chart (U,
<p)
in M and every chart (V, Ik) in N, the composite map Ik0 f 0
<p-l
:
R
m
~
R", called the coordinate expression
for
I, is e
oo
wherever it is defined.
2
The content of this definitionis illustrated in Figure 26.4. A particularfy
im-
portant specialcaseoccurswhen N = R; then we call f a (real-valued) function.
The collection of all
e
oo
functions at a point P E M is denoted by
FOO(P):
If
f E
FOO(P),
then f : Up
~
R is e
oo
for some neighborhood Up of P. Let
f :M
~
N be a differentiablemap.Then f is automaticallycontinuous.Nowlet
V bean opensubsetof N. The set
f-I(V)
is anopen subsetof MbyProposition
3
16.4.6.
26.1.10.Proposition.
Let
M be an m-dimensional manifold, f : M
~
N a
differentiable map, and V an open subset
of
N. Then
f-I(V),
the set
of
points
of
M mapped onto V, is an open m-dimensional submanifold
of
M.
Just as the concept of isomorphismidentifiedall vector spaces,algebras,and
groupsthatwereequivalenttooneanother,it is desirableto introducea notionthat
bringstogetherthosemanifoldsthat "look alike."
26.1.11.Definition.
A bijective differentiable map whose inverse isalso differen-
tiable is called adiffeomorphism. Twomanifoldsbetween which a diffeomorphism
exists are called diffeomorphic.
Let
M and N be manifolds. M issaid to be diffeo-
morphic to N at P
E M
if
there is a neighborhood U
of
P and a diffeomorphism
f:
U
~
feU).
Then f iscalled a local diffeomorphism at P.
2The domain
of
J.L
0 f 0 (,0-1 is not all
of
R",
but only its open subset rp(U). However, we shall continue to abuse the notation
and write
jRm
instead
of
rp(U). This way, we do not have to constantly change the domain as U changes. The domain is always
clew
from the context.
Although Proposition 16.4.6 was shown for
Donned linear spaces, it really holds for all "spaces" for which the concept
of
open set is defined.

26.1 DIFFERENTIABLE MANIFOLDS
769
(26.1)
for i = 1,2,
...
,n.
In our discussion of groups, we saw that the set of linear isomorphisms of a
vector space
Vanta
itselfforms a group
GL(V).
The set
of
diffeomorphisms of a
manifold
M onto itselfalso forms a group, which is denoted by
Diff(M).
26.1.12. Example. The
generalization
ofa
sphere
istheunita-sphere,
which
isa
subset
of
JRn+
I defined by
Sn =
(xI,
..
"
Xn+l)
E JRn+ll
xf
+ ...
+X~+l
=
I).
The
stereographic
projection
definesanatlasfor Sn asfollows. Forallpointsof Snexcept
(0,0,
...
, I), the
north
pate, define the
cbart
9'+ :
S"
- (II '" U+
-+
JRn
by
'P+(Xb
...•
X
n+l )
= (
Xl,
...•
t x
n
.)
for(xl.
...•
X
n+l)EU+.
1 - x
n
+l - x
n
+l
To
include
the
north
pole,
consider
a second
chart
ip.: : Sn -
{-I}
==
U-
-+
R"
defined
by
CP-(xI
•...
, X
n
+ l )
= ( Xl ,
...
, I X
n
)
1+X
n+l
+X
n+l
Next,letus
find
the
inverses
of these
maps.
We
find
the
inverse
of
'P+:
that
of
C}J-
can
be found similarly.
Let
~k
ee
Xk/(t
-
x"H)'
Then
one
can
readily
sbow
that
f--.2
I+xn+t
EZ-l~l+1
L5k
=
=>
xn+ l = 2
k=l
I -
Xn+t
EZ=1
~k
- I
and
2~i
Xi
=-:-1
-_-=,,=n=--=."2
L..k=1 >k
From
the
definition
of
CP+.
wehave
9':;:1
(~j,
...
,
~n)
=
(XI,
...
, X
n,
X
n+l)
= ( .
2?
2"'"
2~
2'
E~-l~~+I).
I- E
k
=l
~k
I- E
k
=l
~k
E
k
= l
~k
- I
On the
overlap
of
U+
and
U-,
i.e., onall
points
of Sn exceptthe
north
and
the
south
poles,<p_ 0
<p.+
1
:
IR
n
-+
IRn
canbe
calculated
by
noting
that
<p_ hasthefollowing effect
on a typical entry
of
Eqnation
(26.1):
2~j
n-sphere
and
its
stereographic
projection
diffeomorphlsms
ofa
manifold
form
a
group
Therefore,
-I
.)
(~I
~n
)
<p_oCfJ+
(';lo
..
·,sn
= n
2"'"
n
2'
E
k
= l
~k
E
k
=l
~k
It
is
clear
that
CfJ-
0
CfJ'+
1
has
derivatives
of all
orders
exceptpossiblyatapointforwhich
';i
= 0 foralli. But this
would
correspond
tox
n
+ l = 1,
which
is
excluded
from the
region
of
overlap.
II
770
26. ANALYSIS
OF
TENSORS
M
IFIlm
f
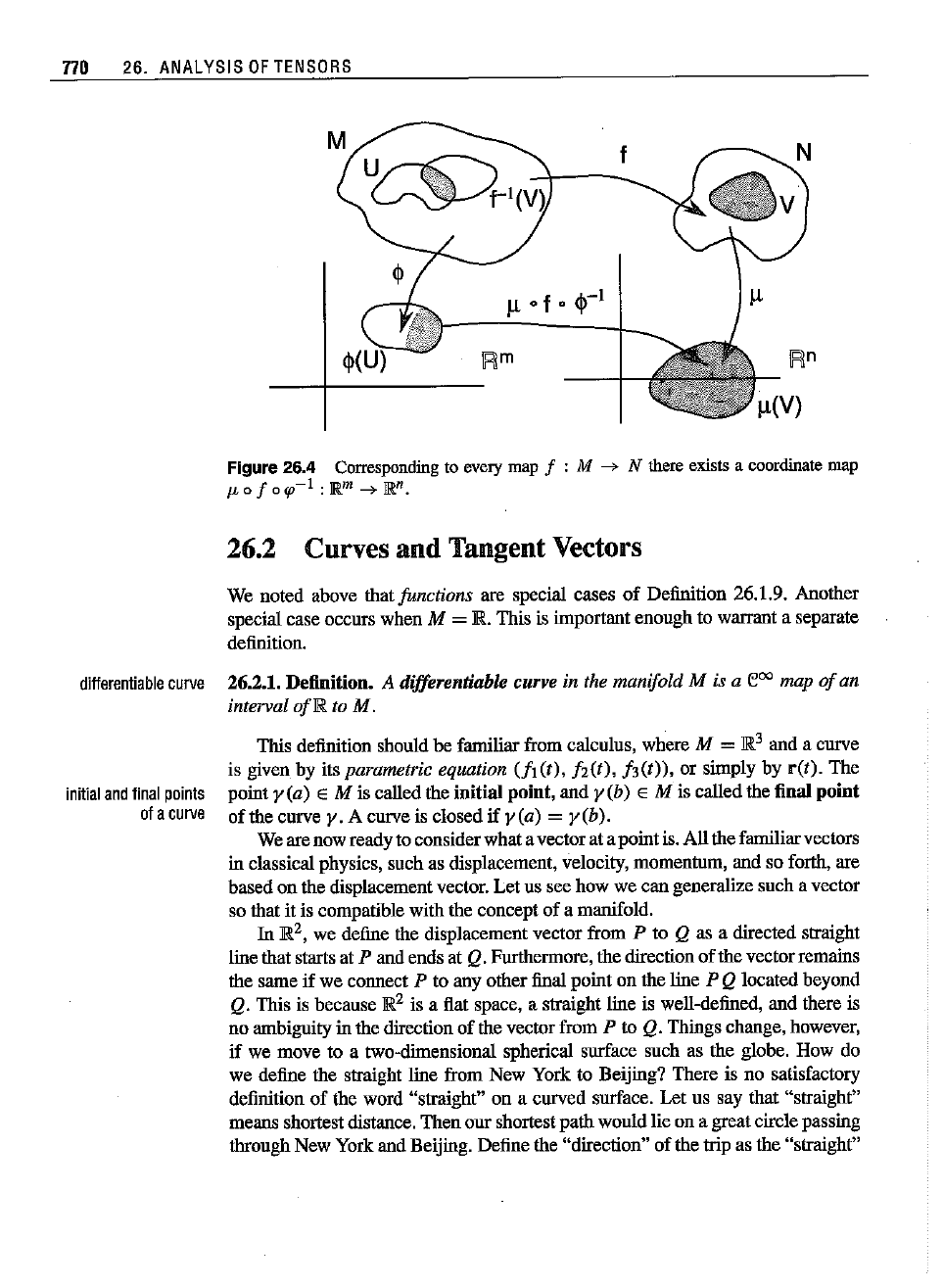
Figure
26.4
Corresponding to every map f : M
---+
N there exists a coordinatemap
JLO
f
o<p-l
: lR
1n
-+
IPt,n.
26.2 Curves and TangentVectors
We noted above that functions are special cases
of
Definition 26.1.9. Another
special case occurs when
M = R. This is important enough to warrant a separate
definition.
differentiable
curve
26.2.1. Definition. A differentiable curve in the manifold M is a e
oo
map
of
an
interval
of~
to M.
This definition should be familiar from calculus, where M =
~3
and a curve
is given by its
parametric equation (11(t),
h(t),
/3(t)), or simply by ret). The
initial
and
linal
points
poiot yea) E M is called the initial point, and
y(b)
E M is called the final point
01
a
curve
of the curve y. A curve is closed
if
yea) = y(b).
Weare now ready to considerwhata vectorat apoiotis. All the familiarvectors
io classical physics, such as displacement, velocity, momentum, and so forth, are
based on the displacement vector. Let us see how we
can
generalize such a vector
so that it is compatible with the concept of a manifold.
In
~2,
we define the displacement vector from P to Q as a directed straight
lioe that starts at
P and ends at Q.Furthermore, the direction of the vectorremaios
the same if we connect
P to any other final poiot on the lioe PQ located beyond
Q. This is because
~2
is a flat space, a straight lioe is well-defined, and there is
no ambiguity io the direction
of
the vector from P to Q.Thiogs change, however,
if we move to a two-dimensional spherical surface such as the globe. How do
we define the straight lioe from New York to Beijiog? There is no satisfactory
definition of the word "straight" on a curved surface.
Let
us say that "straight"
means shortest distance. Thenour shortestpathwould lie on a great circle passiog
through New York and Beijiog. Define the "direction" of the trip as the "straight"

26.2
CURVES
AND
TANGENT
VECTORS
771
arrow, say I km in length, connecting
our
present position to the next point I km
away. As we move from New York to Beijing, going westward, the tip of the arrow
keeps changing direction. Its direction in New York is slightly different from its
direction in Chicago.
InSan Francisco the direction is changed even more, and
by the time we reach Beijing, the tip
of
the arrow will be almost opposite to its
original direction.
The reason for such a changing arrow is,
of
course, the curvature of the manic
fold. We can minimize this curvature effect
if
we do not go too far from New York.
If
we stay close to New York, the surface
of
the earth appears flat, and we can draw
arrows between points. The closer the two points, the better the approximation
to flatness. Clearly, the concept
of
a vector is a local concept, and the process
of
constructing a vectoris a limiting process.
The limiting process in the globe example entailed the notions of "closeness."
Such a notion requires the concept
of
distance, which is natural for a globe but
not necessary for a general manifold. For most manifolds it is possible
to define
a metric that gives the "distance" between two points of the manifold. However,
the concept of a vector is too general to require such an elaborate stmcture as a
metric. The abstractusefulness of a metric is a result
of
its real-valucdness: given
two points PI and
P2,the distance betweenthem,
d(Pj,
P2), is a nonnegative real
number. Thus, distances between different points can be compared.
We have already defined two concepts for manifolds (more basic than the
concept of a metric) that together can replace the concept of a metric in defining
a vector as a limit. These are the concepts
of
(real-valued) functions and curves.
Letus see how functions andcurvescanreplacemetries.
Let y : [a, b] --> M be a curve in the manifold M.
Let
P E M be a point
of
M that lies on y such that
y(c)
= P for some c E [a, b].
Let
f E FOO(P).
Restrict f to the neighboringpointsof P that lie on y. Then the compositefunction
f 0 y : R --> R is a real-valued function on R.
We can compare values
of
f 0 y for various real numbers close to
c-as
in
calculus.
If
U E [a, b] denotes" the variable, then f 0
y(u)
=
f(y(u))
gives the
value
of
f 0 y at various
u's.
In particular, the difference
!'1(f
0
y)
sa
f(y(u»
-
f(y(c))
is a measure of how close the point
y(u)
E M is to P. Going one step
further, we define
d(~:
y)
I.=c
=
Y-Tc
f(Y(U)~
=
:(y(C))
,
(26.2)
the usual derivative of an ordinaryfunction of one variable. However, this derivative
depends on
y and on the point P. The function f is merely a test function. We
could choose any other function to test how things change with movement along
y.
Whatis important is not whichfunction we choose, but how the curve y causes
it to change with movement along
y away from P. This change is determined by
4Weusuallyuse u ort to denotethe(real)
argument
of the mapy : [a, b] --+ M.

772
26. ANALYSIS
OF
TENSORS
illustration
of
the
equality
of
vectors
and
directional
derivatives
the directional derivative along y at P, as given by (26.2). A directional derivative
determines a tangent which, in turn, suggests a tangent vector. That is why the
tangent vector at
P along y is defined to be the directional derivative itself!
The use of derivative as tangent vector may appear strange to the novice,
especially physicists encountering it for the first time, but it has been familiar to
mathematicians for a long time.
It
is hard for the beginner to imagine vectors
being chargedwith the responsibility
of
measuring the rate
of
changeof functions.
It
takes some mental adjustment to get used to this idea. The following simple
illustration may help with establishing the vector-derivative connection.
26.2.2.
Example. Let us take the familiar case
of
a plane and consider the vector a =
axe
x
+ayeyo
What
kindof a
directional
derivative
can
correspond
to a?
First
weneeda
curve
y : IR
-+
]R2
that
is
somehow
associated
witha. It is not
hard
to
convince
oneself
thatthemost
natural
association is
that
of vectorsto
tangents.
Thus,we seeka curvewhose
tangentis (paral1elto) a. The easiest(but not the only) way is simply to take the straight line
alonga;
that
is, let
y(u)
= (axu,
ayu).
The
directional
derivative
att =0 foran
arbitrary
functionf :
]R2
--+
lR
is givenby
d(f
0 y) I = lim
f(y(u»
-
f(y(O»
= lim
f(ax
u,
ayu) - f(O,
0).
du
u=O
U--70
U u-*O U
Taylor
expansion
intwo
dimensions
yields
afl
afl
f(ax
u,
ayu)
= f(O, 0) +aeu
-a
+ayu
-a
+....
x
u=o
y
u=o
(26.3)
tangent
vector
defined
derivation
properly
of
tangent
vectors
Substituting in (26.3), we obtain
d(f
0 y) I = lim
axu(af/ax)u~o
+
ayu(af/ay)u~o
+...
du
u=Q u-+O U
af af
(a
a)
= axax +ay ay = ax ax +ay ay f.
This
clearly
showsthe
connection
between
directional
derivatives
and
vectors.
In
fact,
the
correspondences
aI
ax
#
ex
anda
lay
#
ey
establish
this
connection
very
naturally.
Note
that
the
curve
y chosen
above
is byno
means
unique.
In fact,
there
are
infinitely
many
curves
that
havethesame
tangent
att = aandgive thesame
directional
deriva-
ti~.
•
Since
vectors
arethesameas
derivatives,
weexpectthemtohavethe
properties
shared by derivatives:
26.2.3.Definition.
Let
M bea differentiable manifold.A
tangent
vector at P E M
is an operator
t : Foo(P)
--+
R such that
for
every
f,
g E Foo(P) and
ex,
fJ
E R
1. t is linear: t(exf +fJg) = ext(!) +fJt(g);
2. t satisfies the derivation property:
l(fg)
=
g(P)t(f)
+
f(P)I(g).
