Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations

Подождите немного. Документ загружается.

17.1 CLASSIFICATION 493

in Chapter 6. Thus, for instance,

3(x,

(xl

K(l

IsIl (sll

dSI)K

IS2)

(s21

dS2)

Kit}

}

= Iv}

+).K

[u) +

...

+ ).nK

Iv} =

L().K)i

Iv} ,

i~O

whose integral form is

(17.8)

(17.9)

Un(x) =

t).i

Ki(x,t)v(t)dt.

j=O

Here Ki (x, t) is defined inductively by

KO(x, z) = (xl

It) =

(xI1It)

(xl

t) =

8(x

t),

Ki (x, t) = (xl

KKi-

It) = (xl K

Is) (si

dS)

Ki-

It}

= l

K(x,s)Ki-l(s,t)ds.

The limit

(x)

as n

gives

u(x)

f).i

Ki(x,

t)v(t)dt.

(17.10)

j=O

The

convergence

this series, called the Neumann series, is always guaranteed

for the Volterra equation.

For

the Fredholmequation, we

need

to impose the extra

condition

1).IIIKIl

< 1.

17.1.4. Example. As an example, let us find the solution of u(x) = 1

+).

u(t) dt, a

Volterra equation of the second kind. Here,

v(x) = I and K(x, t) = 1, and it is straightfor-

ward

calculate

approximations

to u(x):

Uo(x)

=v(x) =1,

UI(X)

foX

K(x,t)uo(t)dt

=1 +AX,

{X . (X

A2X2

U2(X)

K(x,t)uI(t)dt

= 1

+M)dt

=I +AX +

-2-'

494 17.

INTEGRAL

EQUATIONS

It is

clear

that the

nth

term will

look

).,2

).}lXn

)jx

u,,(x) =

l+h+--+

...

+-,-

= L-.,-.

2 n.

j=O

As n --+

00,

we obtain

u(x)

= e

• By direct substitution, it is readily checked that this is

indeed a solution of the original integral equation. II

17.2 Fredholm Integral Equations

We can use our knowledge

compactoperators gainedin the previous chapter to

study Fredholm equations

the secondkind. With A "" 0 a complex number, we

consider the characteristic equation

(l-AK)lu)

= Iv), or

u(x)

AK[u](x)

v(x),

(17.11)

where

all fuuctious are square-integrable on [a, bl, and

K(x,

t), the

Hilbert-

Schmidtkernel, is square-integrable on the rectangle [a, bl x [a, b].

Using Propositiou 16.2.9, we innnediately see that Equation (17.11) has a

unique solutiou if

IAIIiKIl

< I,

and

the solutiou is

theform

lu) = (1 - AK)-llv) =

LA"K"

Iv),

n=O

(17.12)

u(x)

L~oAnK"[vl(x),

where

Kn[v](x)

is defined as in Equation (17.4)

except that now

b replaces x as the upper limit

integration.

17.2.1.

Example.

Considerthe integralequation

u(x)

K(x,

t)u(t)

dt = x, where

{

ifO~x

<t,

K(x,

r) = t

ift

<x::::::

Here )" = 1; therefore, a Neumann series solution exists if

IIKIf

< 1.

is convenient to

write K

in terms

the thetafunction:

K(x,

t) = xO(t - x) +

to(x

- r),

(17.13)

This gives

IK(x, t)1

= x

20Ct

- x) +t

20(x

- t) because 02(x - t) = O(x - t) aod

O(x - t)O(t - x) =

Thus,we have

IIKII

= f

dtIK(x,

t)1

fo1dx

folx20Ct-X)dt+

fo1dx

1t2

0(X-t)dt

(t3)

)

= fo dt fo x

dx +f

dt = f

+fo dx 3" = 6'

1Recall

that

the theta function is defined to be 1

its argument is positive, and 0

it is negative.

17.2

FREDHOLM

INTEGRAL

EQUATIONS

495

Sincethisis less

than

I, the

Neumann

series

converges,

andwehave

u(x)

I»

Ki(x,t)v(t)dt=

flo

Ki(x,t)tdt=

ffi(x).

j=O

a j=O 0

j=O

The firstfew terms areevaluatedas follows:

fo(x) =

KO(x,t)tdt

8(x,t)tdt

!J(x)

K(x,t)tdt=

(I[X8(t-X)+t8(x-t)]tdt

=x 1

_ x

x 1

2 6

Thenextterm is

trickier

than

the

first

two

because

ofthe

product

ofthe

theta

functions.

We first substitute Equation (17.13) in the integral for the second-order term, and simplify

h(x)

2(x,t)tdt

tdt

K(x,s)K(s,t)ds

t dt

[x8(s - x) +sO(x - s)][sO(t - s) +tOrs - t)] ds

tdt

sO(s-x)8(t-s)ds+x

2dt

O(s-x)8(s-t)ds

(\dt

0(x-s)8(t-s)ds+

t2dt

(\O(X-s)O(s-t)ds.

Itis convenientto

switch

the

order

integration

atthispoint, Thisis

because

ofthe

presence

ofO(x - s) and O(s

-x),

which do not involve t and are bestintegrated last. Thus, we have

h(x)

s8(s-x)ds

/,1

tdt+x

8(s-x)ds

loS

2dt

foIS20(X-S)dS

/,I

t d

foIS8(X-S)dS

2dt

=x1IsdS(~_s2)+x11

(Xs2dS(~_s2)+

f'sds

x 2 2 x 3

2 2 1

5 1 3 1 5

=-x--x

+-x

24 12 120

As a test of his/her knowledge of O-function manipulation, the reader is orged to perform

the

integration

reverse

order.

Addingalltheterms, we

obtain

approximation

foru(x)

that

is validfor0::: x

:::

2Note

that

inthiscase

(Fredholm

equation),

wecan

calculate

the

jth

terminisolation. In the

Volterra

case,itwasmore

natural

calculate

thesolutionup to agiven

order.

496 17.

INTEGRAL

EQUATIONS

We have seen that the Volterra equation of the second kind has a unique so-

lution which can be written as an infinite series (see Theorem 17.1.2). The case

of the Fredholm equation

the second kind is more complicated because of the

existence

eigenvalues. The general solution of Equation (17.11) is discussed in

the following:

Fredholm

alternative

17.2.2.

Theorem.

(Fredhohn Alternative) Let K be a Hilbert-Schmidt operator

and

A a complex number. Then either

1. A is a regular value

Equation (17.11)---or A

-I

is a regular point

ofthe

operator

K-in

which case the equation has the unique solution lu) = (1 -

AK)-I Iv), or

2. A is a characteristic value

Equation (17.11) (A

-1

is an eigenvalue

ofthe

operator K), in which case the equation has a solution if and only if Iv)

is in the orthogonal complement

the (finite-dimensional) null space

1-A*Kt.

Proof The first partis trivial if we recall that by definition, regularpoints of Kare

those complex numbers

fl. which make the operator K-

fl.1

invertible.

For

part (2), we first show that the null space of 1 - A*Kt is finite-dimensional.

We note that 1 -

is invertible if and only if its adjoint 1 - A*Kt is invertible,

and A

E P(K) iff

1.*

E P(Kt). Since the specttum of an operator is composed of

all points that are not regular, we conclude that A is in the specttum of K

and

only

1.*

is in the specttum of Kt. For compact operators, all nonzero points of

the specttum are eigenvalues. Therefore, the nonzero points of the specttum of

Kt, a compactoperator by Theorem 16.5.7, are all eigenvalues

Kt, and the nnll

space

1 - A*Kt is finite-dimensional (Theorem 16.6.2). Next, we note that the

equation itselfrequires that

Iv) be in the range

the operator 1 -

AK,

which, by

Theorem 16.6.2, is the orthogonal complement

the nnll space

of1

- A*Kt. D

Erik

IvarFredholm (1866-1927) was born inStockholm, the

sonof awell-to-do

merchant

family.

received

thebestedu-

cationpossibleandsoonshowedgreatpromiseinmathematics,

leaningespecially

toward

the

applied

mathematics

practi-

cal mechanics in a year

study at Stockholm's Polytechnic

Institute.

Fredholm

finished

his

education

attheUniversity of

Uppsala, obtaining his doctorate in 1898. He also studied at

the

University

Stockholm

during

thissameperiodandeven-

tuallyreceivedan

appointment

to the

faculty

there.

Fredholm

remained

there

therestof hisprofessional life.

His

first

contribution

mathematics

was

contained

inhis

doctoral

thesis,in whichhe

studied

first-order

partial

differential

equation

three

vari-

ables, a

problem

that

arises

in the

deformation

anisotropic

'media.

Several

years

later

17.2

FREDHOLM

INTEGRAL

EQUATlDNS

497

he completedthis work by

finding

the fundamental solntion to a general elliptic partial

differential

equation

with

constant

coefficients.

Fredholm

perhaps

bestknownforhis

studies

of the

integral

equation

that

bears

his

name.

Such

equations

occur

frequently

in physics.

Fredholm's

geniusled himto notethe

similarity

betweenhis

equation

andarelatively

familiar

matrix-vector

equation,

resulting

inhis

identification

of a

quantity

that

playsthesameroleinhis

equation

asthe

determinant

playsinthematrix-vector

equation.

Hethusobtainedamethodfordeterminingtheexistence

of a

solution

and

later

usedan

analogous

expression to

derive

solution

to his

equation

akintothe

Cramer's

rulesolution to the

matrix-vector

equation.

further

showed

that

the

solution could

expressed

asa powerseriesin a complex

variable.

This

latter

resultwas

considered

important

enoughthat

Poincare

assumed

without

proof(infacthe was

unable

prove

it)ina

study

partial

differential

equations.

Fredholm

then

considered

the homogeneous

form

of his

equation.

He showedthat

under

certain

conditions, the vectorspaceof solutionsis

finite-dimensional.

David

Hilbert

later

extended

Fredholm's

worktoacompleteeigenvalue

theory

of the

Fredholm

equation,

whichultimately ledtothediscovery of

Hilbert

spaces.

17.2.1 HermitianKernel

special interest are integral equations in which the kernel is hermitian, which

occursexactly when the operatoris hermitian. Sucha kernel has the property thar'

(r] K[r)"

= (tl KIx) or

[K(x,

t)]*

K(t,

x).

For

such kernels we

can

use the

spectral theorem for compact hermitian operators to find a series solution for the

integral equation. First we recall that

where we have used

J..

to denote the eigenvalue

the operator" and expanded

the projection operatorin terms

orthonormal basisvectors

the corresponding

finite-dimensional eigenspace. Recall that

can

be infinity. Instead

the double

sum, we can sum once over

allthe basisvectors and write K =

L:~I

J..;llu

(unl·

Here n counts all the orthonormal eigenvectors

the Hilbert space, and J..;1is the

eigenvalue corresponding to the eigenvector

n).

Therefore, J..;I may be repeated

in the sum.

The

action

Kon a vector Iu} is given by

lu)

I>;I

(unl u) lu

n).

11=1

(17.14)

3Sincewe aredealingmainlywithreal

functions,

hermiticity

of Kimpliesthe

symmetry

of K, i.e., K (x, t) = K (t,

x).

4)"

j is the

characteristic

valueof the

integral

equation,

orthe

inverse

of theeigenvalue of the

corresponding

operator.

498 17.

INTEGRAL

EQUATIONS

If the Hilbert space is

.(,2[0,

b],we may be interested in the functional form of this

equation. Weobtain such a form by multiplying both sides by (x

00 00

K[u](x)

(xIKlu) =

I);!

(unlu)

(xlu

I);l

(unlu)un(x).

n=l

(17.15)

Hilbert-Schmidt

theorem

That this series convergesuniformly in the interval [0, b] is known as the

Hilbert-

Schmidt theorem.

17.2.3. Example. Letus

solve

u(x)

=x +A

K(x,

t)u(t)dt,

where

K(x,

symmetric

(hermitian)

kernel,

by the

Neumann

series

method.

Wenote

that

IIKII

= l

IK(x,t)1

2dxdt

= l

2dxdt

x2dx

t2dt

2dX)

~(b3

_ a

)2,

IIKII

= l

2dx

!(b

andthe

Neumann

series

converges

I)..

I(b

- a

)

< 3.

Assuming

that

thisconditionholds;

we have

u(x)

= x +

I>i

Ki(x,

t)tdt.

j=l

The

specIal

formofthe

kernel

allows

usto

calculate

(x, t)

directly:

Ki(x,t)

= l

K(x,SI)K(s!,S2)

...

·K(si_J,t)dslds2···dsi_l

b···l

xsfs~

...

S~_ltdslds2···

dSj_l

a a a J

(

1s2 ds = xtllKlli-

follows

that

(x,

t)t

dt = xIlKlli-

1!(b

) = xllKlli.

Substituting

thisinthe

expression for

u(x)

yields

00 00

u(x) =x +

I>ixlIKlli

+xAIiKII

I>i-11IKll

j=l

+AIIKIII_~IIKII)

I-:IIKII

Becauseofthesimplicity of the

kernel,

wecansolvethe

integral

equation

exactly.

First

wewrite

u(x)

= x + Al

xtu(t)

dt =x +

tu(t)

x(1

+ AA),

17.2

FREDHDLM

INTEGRAL

EQUATIDNS

499

whereA =

tu(t) dt. Multiplying both sidesbyx audintegrating, we obtain

A = lab

xu(x)dx

= (I

+AA)

lab x

2dx

+AA)

KII

A = I

~~::KII

Substitutiug A in Equation(17.15)gives

_ ( A

IIKII

) _ x

u(x) - x 1+

AIIKII

AIIKII"

Thissolution is thesameasthe

first

onewe

obtained.

However,

noserieswasinvolvedhere,

and

therefore

assumption

necessary

concerning

l'AIIiKIl.

one cau calculate the eigenvectors Iun} and the eigenvalues A;;

then one

can obtain a solution for the integral equation in terms of these eigenfunctions as

follows: Substitute (17.14) in the Fredholm equation [Equation (17.3)] to get

lu) = Iv) +A

~:::>;;1

(unl u) Iu

n).

n=l

Multiply both sides by (u

(17.16)

(uml u) = (uml v) +A

LA;;1

(unl u) (uml un) = (uml v) +).).;;;1 (uml U),

n=1

(17.17)

or,if

)..

is notoneof theeigenvalues.

(

- Am(umlv)

Urn U - .

- A

Substituting this in Equation (17.16) gives

(unl v)

lu} = Iv) +A

A _ A Iu

n),

n=l

and in the functional form,

(unl v)

u(x)

v(x)

-r-r--r-un

(x),

n=l

- A

(17.18)

(17.19)

In case

A =

for some m, the Fredholm alternative (Theorem 17.2.2) says

that we will have a solution only

Iv) is in the orthogonal complementof the null

space of

1 -

AmK.

Moreover, Equation (17.17) shows that (uml u), the expan-

sion coefficients of the basis vectors of the eigenspace

cannot be specified.

5Remember

thatKis hermitian;

therefore,

isreal.

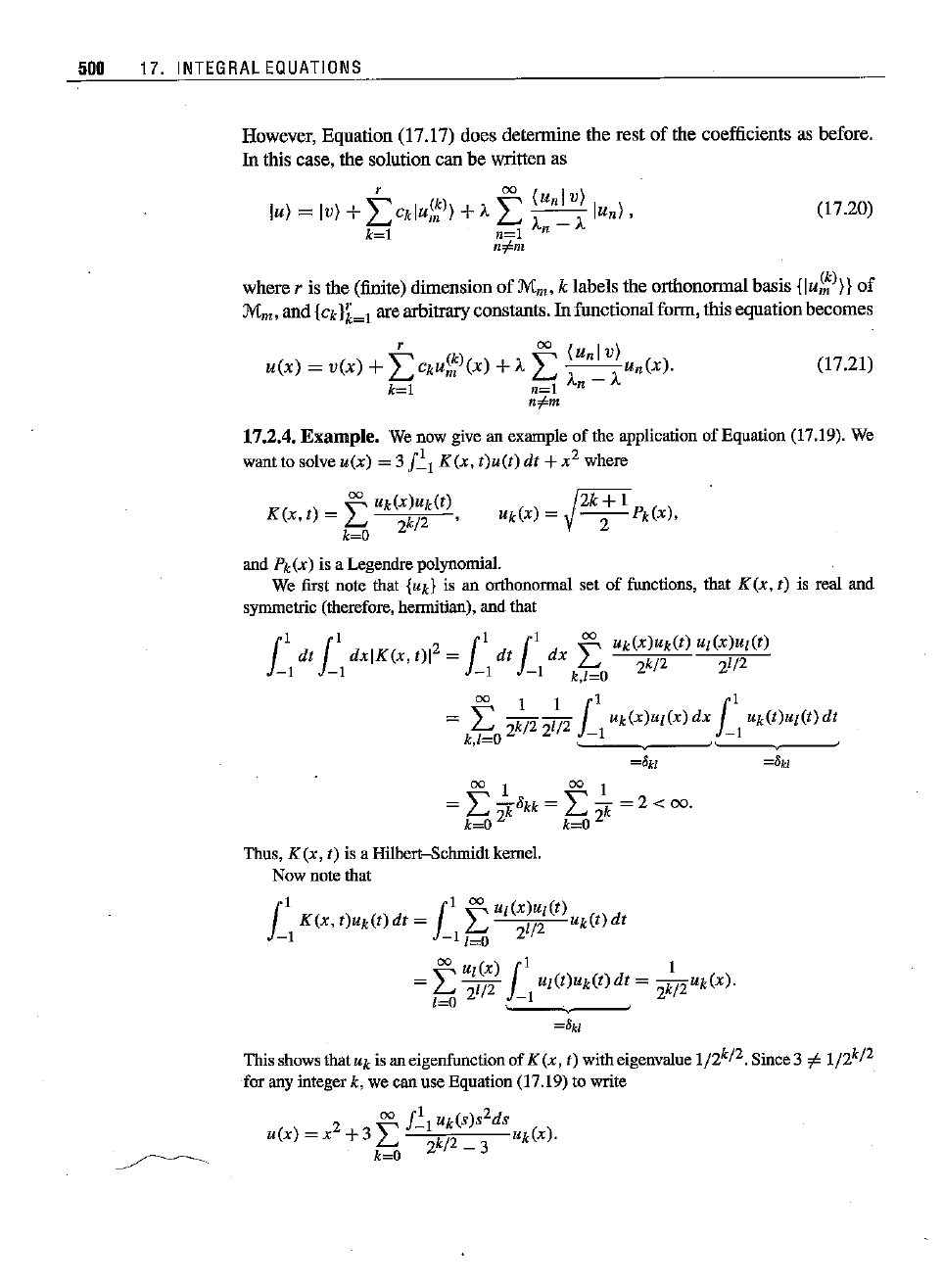
(17.20)

(17.21)

500 17.

INTEGRAL

EQUATIONS

However, Equation (17.17) does determine the rest

the coefficients as before.

this case, the solution can be written as

(k)

(u,,1v)

lu) = Iv) +

L..,

ckl

u",

} +A

L..,

A _ A lu,,),

k=l

11=1

n=f:.m

where r is the (finite) dimension

M"" k labels the

ottbononnal

basis {Iu!:»}

M"" and {Ck

}k~1

are arbitraryconstants.

functionalform, this equationbecomes

(ulv)

u(x)

v(x)

CkU~~)(X)

_n_un(x).

k=l

11=1

- A

n"",

17.2.4. Example. Wenow give an exampleof the applicationof Equation (17.19).We

wantto solve

u(x)

= 3

J~1

K(x,

t)u(t)

where

and

(x)

is a Legendrepolynontial.

first

note

that

{Uk}

is an

orthonormal

set of

functions,

that

K(x,

t) is real and

symmetric (therefore, hermitian), andthat

1 dt 1

dxIK(x,

t)1

= 1

dx t

Uk(X~U:(t)

u/(x;u;(t)

-1

-1 -1 -1

k,/=O 2 / Z /

1 I 1

k/2172

Uk(X)U/(x) dx Uk(t)U/(t) dt

k,/=O

2 2

-I

-1

~~~~

=Okl

=clkl

001

8kk

"k = 2 <

00.

k~O

Z k=OZ

Thus, K (x, t) is a Hilbert-Schutidtkernel.

Now

note that

This

ahows

that zq isaneigenfunctionof

K(x,

r) witheigenvalue

1/2

k/2.

Since3

I/Z

for

any

integer

k,we canuse

Equation

(17.19) to write

J~1

Uk(S)s2ds

u(x)

= x +3

k/2 Uk(X).

k=O Z -

17.2

FREDHDLM

INTEGRAL

EQUATIDNS

501

But

J~I

Uk(S)s2ds =0 fork

2::

3.Fork ::: 2, weuse thefirstthree Legendrepolynomials

to get

1 2 ..ti

uo(s)s ds =

-I

3 1

1 UI(s)s2

= 0,

-I

degenerate

separable

kernel

Thisgives u(x) = !-2x

. The

reader

urged

substitute

thissolution in the

original

integral

equationandverify

that

itworks. II

17.2.2 Degenerate Kernels

The preceding example involves the simplest kind

degenerate, or separable,

kernels.

A kernel is called

degenerate,

separable,

if it cao be written as a finite

sum of products of functions of one variable:

K(x,

I>/>j(x)1frj(t),

j=l

(17.22)

where

<Pj

aod 1frjare assumed to be square-integrable. Substitoting (17.22) in the

Fredhohn integral equation of the second kind, we obtain

u(x)

- A

<Pj

(x) a

1frj(t)u(t)

v(x).

we define f.'j =

1frj(t)u(t)

dt,

the preceding equation becomes

u(x)

- A

Lf.'j<Pj(X)

v(x).

j=l

Multiply this equation by 1frt

(x)

aod integrate over x to get

(17.23)

f.li - A

LfJ-jAij

= Vi

j~l

for i =

...

,n,

(17.24)

where

Aij

1frt(t)<pj(t)

aod Vi =

1frt(t)V(t)

dt.

With f.'i, Vi, aod

Aij

components

column

vectors

u,v,

and

matrix

A,we canwritethe

above

linear

system of equations as

u -

)"Au

= v,

(1-AA)u

=v.

(17.25)

cao

now determine the f.'i by solving the system

linear equations given

by (i7.24). Once the

f.'i are determined, Equation (17.23) gives

u(x).

Thus, for a

degenerate kernel the Fredholm problem reduces to a system of linear equations.

502 17.

INTEGRAL

EQUATIONS

17.2.5. Example. As a

concrete

example

of an

integral

equation

with

degenerate

kernel,

we solve

u(x)-l

fJ(I+xt)u(t)

=x for two differentvalues ofA.

Thekemel,

K(x,

t) =

xt,

isseparable with

9'>1

(x) = I,

1/Jl

(I)

= I,

9'>2(X)

= x, and

1/J2(t)

= t. This gives the

matrix

t)·

2 3

Forconvenience,we definethe

matrix

Bsa 1 -

)"A.

(a)Firstassume

that)"

= 1.Inthatcase Bhasa nonzero determinant. Thus,

exists,and

canbe calculatedtobe

With

VI = f

1/J;(I)v(t)dt

= f

tdt

and "2 =

1/J

; (I)V(t) dt =

2dt

= j

weobtain

(

fl.I)

B-Iv

(-i

fl.2

-2

Equation

(17.23)

then gives

u(x)

fl.19'>1

(x) +f1.2¢2(x)+x =

-2.

(b) Now, forthe

purpose

illustrating theother

alternative

Theorem 17.2.2,letus

take

l = 8 +

203.

Then

(

203

)

B = 1 - AA = - 4 +

(5 +

203)/3

anddetB=

Thisshowsthat8 +2.../13is acharacteristic value

the

equation.

Wethus

havea solution only

vex)

x is

orthogonal

to thenull

space

of 1 - A*At =

at.

determine

abasisforthisnull

space,

have

find

vectors

Iz)such

that

lz)

Since

). is real,andBisrealandsymmetric, Bt = B,andwe mustsolve

(

203

)

«I)

4 +

(5+

203)/3

Thesolution to this

equation

is a multiple of lz)

(-2!,JI3

).lfthe

integral

equation

is to

havea solution,thecolumnvectorv (whosecorresponding ketwe denote

by Iv)) mustbe

orthogonal to lz). But

(zl v) = (3

-2

03)

(t)

Therefore,

the

integral

equationhasno solution.

III