Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.

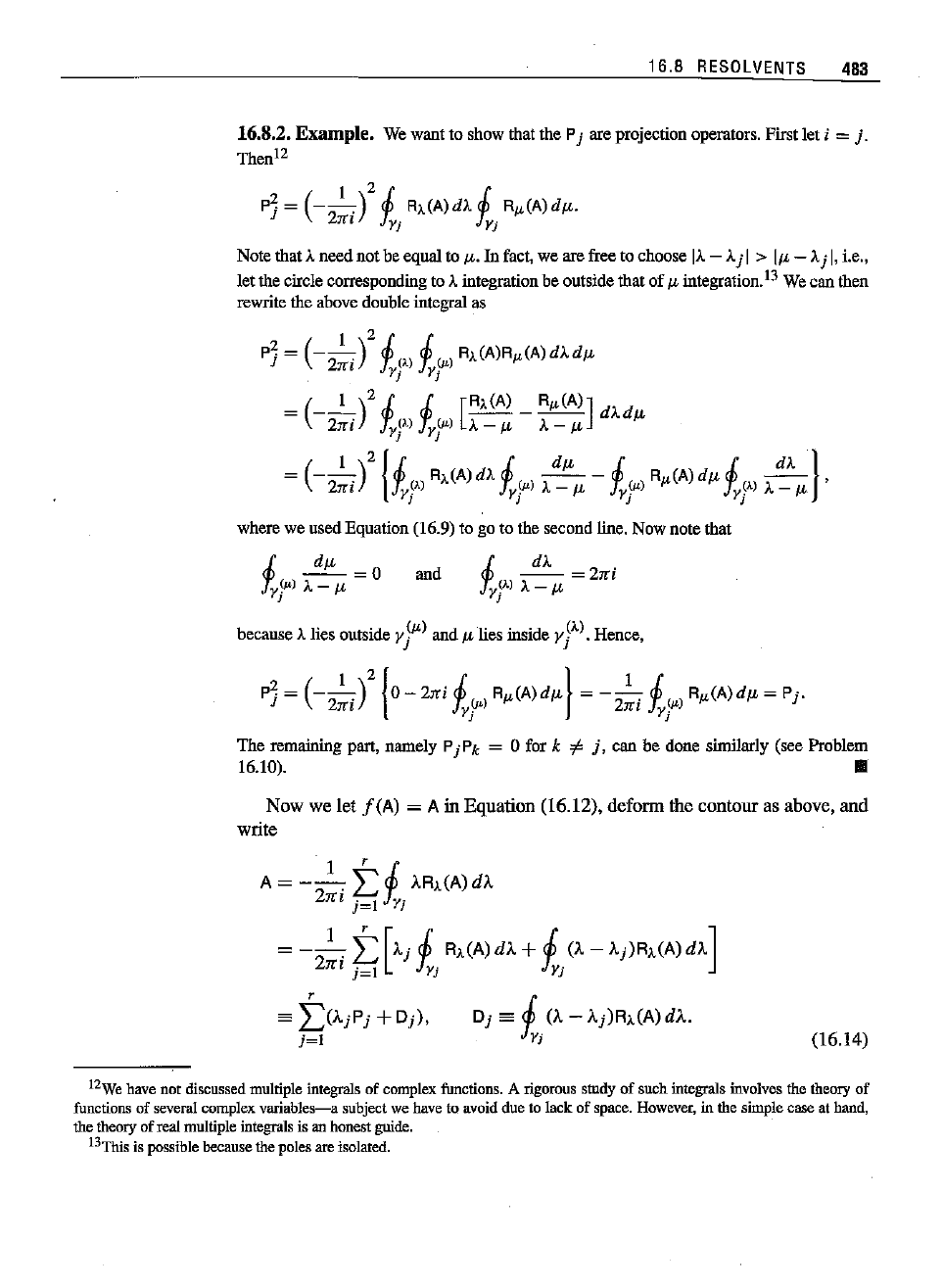
16.8
RESOLVENTS
483
16.8.2.
Example.
We want to show that the Pj are projection operators. First let i =
j.
Then
12
P]
= (
__
1_.)2
1.
R)JA)dA
1.
Rtt(A)dl-'.
27l'Z
t;
jYi
Note that Aneed not be equal to
1-'.
In fact, we are free to choose
IA
- Aj I >
II-'
- Aj I,i.e.,
letthecircle
corresponding
to
)..
integration
beoutsidethatof
JL
integration.U Wecanthen
rewrite
theabovedouble
integral
as
P]
= (_f)2
1.
(')
1.
V»
Rie(A)Rtt(A)dAdl-'
1rl
ir
j
ir
j
= (
__
I
)21.
1.
[Rie(A) _ Rtt(A)]
dAdl-'
21ri
1'r~},.)
J;,~)
)..
-
JL
J...
-
JL
I I
=
h~J
{it,)
Rie(A)
dA
i(.)
A
~
I-' -
i<.)
Rtt(A)du:
it,)
A
~
I-'} ,
J J J J
wherewe used Equation (16.9) to go to thesecondline. Now notethat
and
i
dA
--
=2rri
y~).)
A-
JL
I
because
Alies
outside
rJIL)
andn lies inside
yy).
Hence,
P] =
(-
2~i)2
{o-
'Ixi
iiV»
Rtt(A)dl-'}
= -
2~i
i
y
)
Rtt(A)dl-' =
Pj.
The remaining part, namely
PjPk
= 0 for k
'"
j,
can be done sbnilarly (see Problem
16.10).
..
Now
we
let
I(A)
= A in
Eqnation
(16.12),
deform
the
contonr
as above,
and
write
(16.14)
12We
havenot discussed multiple
integrals
of complex
functions.
A
rigorous
studyof such
integrals
involvesthe
theory
of
functions
of
several
complexvariables-a subjectwe haveto avoiddue to lack of space.
However,
in thesimplecase at
hand,
the
theory
ofrealmultiple
integrals
is anhonestguide.
13
This
is possiblebecausethepolesareisolated.

484 16.
AN
INTRODUCTION
TO
OPERATOR
THEORY
It
can be shown (see Problem 16.11) that
OJ =
1.
(A - Aj)" R
A
(A)
o:
t;
In particular, since R
A
(A) has only poles as singularities, there exists a positive
integer
m such that OJ' = O.We have
not
yet
made
any assumptions about A.
If
we assume that A is hermitian, for example, theu R
A
(A) will have simple poles
(see Problem 16.12).
It
follows that (A - Aj)RA(A) will be analytic at Aj for all
j =
1,2,oo.,r,andOj
=OiuEquatiou(16.14).
We thus have
,
A=
I>jPj,
)=1
whichis the spectral decomposition discussed in Chapter4. Problem 16.13 shows
that the
Pj are hermitian.
16.8.3.
Example.
Themostgeneral2 x 2 hermitiaomatrixis of theform
A =
(a~l
a
12
) ,
a
l2
aZ2
where
au
andaZ2 are-real
numbers.
Thus,
whichhas
roots
Al = ![411 +a22 -
)(all
- 422)2+
4141212].
A2
=
![all
+a22+
)(all
- a22)2 +
4141212].
The
inverse
of A- A1can
immediately
be
written:
I I (a22 - A 412 )
R(A)-(A-A1)-
- -
A - -
det(A-A1)
-ai2
411-A
I
(a
Z2
-
A
-a
I2 )
=
(A
-
AI)(A
-
A2)
-ah
411
- A .
Wewantto verify that
R).
(A)has only simple poles. Twocases arise:
1.
If
Al
i'
A2,
thenit is clearthat R
A
(A)
has simplepoles.
2.
If
Al =
A2,
itappears
that
R}"
(A)
mayhaveapole of
order
2.
However,
notethat
if
Al = A2.thenthe
square
rootsintheabove equationsmustvanish.This happensiff
all
=aZ2 sa a and
aiz
=
O.
It
then follows that
A}
=
A2
==
a, and
I
(4-A
0)
RA(A)
=
(A-a)2
0
a-A'
This clearlyshowsthat
RA(A)
has only simplepolesin dtis case.
III

Jordan
canonical
form
16.9
PROBLEMS
485
If
A is not hermitian, Dj
oF
0; however, Dj is nevertheless nilpotent. That
is,
Dj'
= 0 for some positive integer m. This property and Equation (16.14) can
be used to show that
A can be cast into a Jordan canonical
form
via a similarity
transformation. That is, there exists an
N x N matrix S such that
("'
0 0 ...
n
SAS-
1
= J = I
J2
0
...
0
0
where Jk is a matrix
of
the form
A I
0 0
0 0
0
A I
0
0 0
Jk =
0 0 A I 0 0
0 0 0 0
A I
in which A is one
of
the eigenvalnes
of
A. Different Jk
may
contain the same
eigenvalues of A. Fora discussion of theJordan
canonical
form of a
matrix,
see
[Birk 77], [Denn 67], or [Halm 58].
16.9 Problems
16.1. Suppose that S is a bounded operator, T an invertible operator, and that
Show that S is invertible. Hint: Show that
T-
1
S is invertible. Thus, an operator
that
is "sufficiently close"to an
invertible
operator
is
invertible.
16.2.
Let
V and W be finite-dimensional vector spaces. Show
that
T E .G(V,W)
is necessarily bounded.
16.3.
Let
Jf
be a Hilbert space, and T E .G(Jf) an isometry, i.e., a linear operator
that does not change the norm
of
any vector. Show that
IITII
= 1.
16.4.
Show that (a) the unit operator is not compact, and that (b) the inverse
of
a compact operator cannot be bounded. Hint: For (b) use the resnlts
of
Example
16.5.3.
16.5. Prove Corollary 16.6.7. Hint: Let [x) E Ni
q
+
l
)
and writeit as [x) =
In)+
Ir)
with In) E Ni
q)
and Ir) E
:1<i
q).
Apply (K - A
1)q+1
to [r), and invoke part (3)
of
Theorem 16.6.6 to show that Ir) E Ni
q).
Conclude that Ir) =0,
Niq+l)
=Ni
q)
,

486
16.
AN
INTROOUCTION
TO
OPERATOR
THEORY
and q 2: p. To establish the reverse inequality, apply (K -
I-.l)P
to both sides
of
the direct sum
of
part
(I)
of Theorem 16.6.6, and notice that the LHS is
~i.P),
the
second term
of
the RHS is zero, and the first term is
~iq+p).
Now conclude that
p 2:q.
16.6. Let]«) E
~andletMbeasubspaceof1f.ShowthatthesubsetE
=
lu}-M
is convex. Show that E is not necessarily a subspace
of~.
16.7. Show that for any hermitian operator H,we have
4(Hxly}
= (H(x
+Y)lx
+y) - (H(x -
Y)lx
- y)
+i[(H(x +iy)1x +iy} - (H(x - iy)1x -
iy)].
Now let Ix) =
I-.Iz)
and Iy) =
1Hz)
II-.,
where
I-.
= (IIHzll/llzlI)1/2, and show that
IIHzll
2
= {Hx] y) ::: MllzlIlIHzlI,
where
M = maxl] (Hz] z) 1/IIIzIl
2}.
Now conclude that
IIHII
::: M.
16.8. Show that the
twokemels
Kj(x,
r) =
e-
I
x-
tl
and K2(X,
t)
=
sinxt,
where
the first one acts on
,(,2(-00,00)
and the second one on ,(,2(0, 00), have the two
eigenfunctions
and
o at t
V2
e
+ a
2
+t
2
'
respectively, corresponding to the two eigenvalues
a>
0,
2
1-.=I+a
2
'
aEIR,
and
16.9. Derive Equation (16.9). Hint: Multiply
R,,(T)
by 1 =
R"m(T
-
iLl)
and
R"m
by 1 = R,,(T)(T -
1-.1).
16.10. Finish Example 16.8.2by showing that PjPk = 0 for k
i'
j,
16.11. Show thalD) =
:FYi
(I-.
- I-.j)nR"(A)
d):
Hint: Use mathematical induction
and the technique used in Example
16.8.2.
16.12. (a) Take the inner product of lu) = (A -
1-.1)
[u) with Iv) and show that
for a hermitian A,
1m(vi u) =
-(1m
1-.)
IIv
11
2
. Now use the Schwarz inequality to
obtain
IIvll:::
I~~~I
=>
IIR,,(A)lu)lI:::
I~~I~I'
(b) Use this result to show that

16.9
PROBLEMS
487
where eis the angle that A- Aj makes with the real axis and Ais chosen to have
an imaginary part. From this result conclude that
R.
(A) has a simple pole when A
is
hermitian.
16.13. (a) Show that when A is hermitian,
[R.(A)]t
= R•• (A).
(b) Write A - Aj =
rje
ie
in the definition
of
Pj in Equation (16.13). Take the
hermitian conjugate of both sides and use (a) to show that P
j is hermitian. Hint:
You will have to change the variable of integration a number of times.
Additional Readings
1. DeVito, C. Functional Analysis and Linear Operator Theory, Addison-
Wesley, 1990. Our treatment
of
compact operators follows this reference's
discussion.
2. Glimm, J. and Jaffe, A. Quantum Physics, 2nd ed., Springer-Verlag, 1987.
One of the mostmathematicaltreatments
of
the subject,and therefore agood
introduction to operator theory (see the appendix to Part I).
3. Reed, M. and Simon,
B.FourierAnalysis, Self-Adjointness, AcademicPress,
1980.
4. Richtmyer,
R. Principles
of
Advanced Mathematical Physics, Springer-
Verlag, 1978. Discusses resolvents in detail.
5. Zeidler, E.
AppliedFunctional Analysis, Springer-Verlag, 1995.

17
-,------
_
Integral Equations
The beginning of Chapter 16 showed that to solve a vector-operator equation one
transforms it into an equation involving a sum over a discrete index [the matrix
equationofEquation (16.1
n,
or an equationinvolvingan integralover a continuous
index [Equation (16.2)]. The latter is called an
integral
eqnation,
which we shall
investigate here using the machinery of Chapter 16.
17.1 Classification
Volterra
and
Fredholm
equations
offirst
and
second
kind
Integral equations can be divided into two majorgroups. Those that have avariable
limit of integration are called
Volterra
equations; those that have constant limits
of integration are called
Fredholm
equations.
If
the unknown function appears
only inside the integral, the integralequation is said to be of
the
first kind. Integral
equations having the unknown function outside the integral as well as inside are
said to be of
the
second kind. The four kinds of equations can be written as
follows.
Volterra equation
of
the
Ist
kind,
Volterra equation of the 2nd kind,
Fredhohn equation of the Ist kind,
Fredhohn equation of the 2nd kind.
l'
K(x,
t)u(t)
dt
=
v(x),
1
b
K(x,
t)u(t)
dt
=
v(x),
u(x)
=
v(x)
+l'
K(x,
t)u(t)dt,
u(x)
=
v(x)
+1
b
K(x,
t)u(t)dt,
In all these equations, K (x, t) is called the
kernel
of the integral equation.

17.1
CLASSIFICATION
489
In
the theory of integral equations of the second kind, one nsually multiplies
the integral by a nonzero complex number A.Thus, the Fredhohn equation of the
second kind becomes
A Athat satisfies (17.2) with
v(x)
= 0 is called a
characteristic
vaiue of the
integral equation.
In
the abstract operatorlanguage both equations are written as
characteristic
value
of
an
Integral
equation
u(x)
=
v(x)
+A1
b
K(x,
t)u(t)
dt,
and for the Volterra equation
of
the second kind one obtains
u(x)
=
v(x)
+A1
X
K(x,
t)u(t)
dt.
lu} = Iv) +
AK
lu}
=}
(K
- A-I) lu) = -A
-llv).
(17.1)
(17.2)
(17.3)
Thus A is a characteristic value for (17.1) if and only
if
A-1 is an eigenvalue
of
K.Recall that when the interval
of
integration (a, b) is finite,
K(x,
t) is called a
Hilbert-Schmidt kemel. Example 16.5.10 showed that Kis a compact operator,
and by Theorem 16.6.9, the eigenvalues of Keitherform a finite set or a sequence
that
converges to zero.
17.1.1.
Theorem.
The characteristic values
of
a Fredholm equation
of
the second
kind either
form
afinite set or a sequence
of
complex numbers increasing beyond
limit in absolute value.
Our maintask in this chapter is to study methods of solving integral equations
of
the secondkind. We treat the Volterra equationfirst because it is easierto solve.
Let us introduce the notation
K[u](x)
==
1
x
K(x,
t)u(t)
dt
and
Kn[u](x)
=
K[K
n-
1[u]](x)
(17.4)
whereby
K [u1denotes a function whose value at x is given by the integral on the
RHS
of
the first equation in (17.4). One
can
show with little difficulty that the
associated operator
Kis compact. Let M = max{IK (x, t) I Ia ::; t ::; x ::; b} and
note that
IAK[u](x)1 =
IA
1
x
K(x,
t)u(t)
dtl
::;
IAIIMlliulloo(x
-
a),
where
lIulioo
==
max{lu(x)
I I x E (a, b)}.
Usingmathematical induction, one
can
show that (see Problem 17.1)
(x a)n
I(AK)n [u](x) I s
1'-lnlMlnllulioo
,
n.
(17.5)

490 17.
INTEGRAL
EQUATIONS
Since b
2::
x, we can replace x with b and still satisfy the inequality. Then the
inequality
of
Eqnation (17.5) will hold for all x, and we can write the equation as
an operator norm ineqnality:
II
(J.K)n
II
:s:
1J.lnlMl
n
lIu
II
oo(b- a)n
[n':
Therefore,
Volterra
equalion
of
the
second
kind
has
a
unique
solution
and
no
nonzero
characterislic
value
and the series
I:~o(J.K)n
converges for all J..
In
fact, a direct calculation shows
that the series converges to the inverse
of
1 - J.K.Thus, the latter is invertible and
the spectrum
of
Khas no nonzero points. We have
just
shown the following.
17.1.2.
Theorem.
The Volterra equation
of
the second kind has no nonzero char-
acteristic value. In particular, the operator
1 - J.K is invertible, and the Volterra
equation
of
the second kind always has a unique solution given by the conver-
gent infinite series
u(x)
=
I:j:o
J.i
J:
K i (x,
t)v(t)
dt
where Ki (x, t) is defined
inductively in Equation (/7.4).
VitoVolterra (1860-1940)wasonly t1whenhehecameinterested
inrnathematics
while
reading
Legendre's
Geometry. Attheageof 13.
he
began
to
study
the
three
body
problem
and
made
some
progress.
Hisfamilywereextremety poor(hisfatherhaddiedwhenVito
was two yearsold) butafter
attending
lecturesatFlorencehe was
abletoproceedtoPisa
in 1878.AtPisahestudied
under
Betti,
grad-
uating
asa
doctor
of
physics
in 1882.Histhesison
hydrodynamics
included
some
results
of
Stokes,
discovered
later
but
independently
by
Volterra.
He
became
Professor
of
Mechanics
atPisain 1883,andupon
Betti's
death,
he
occupied
the
chair
of
mathematical
physics.
Af-
ter
spending
sometimeat
Turin
as the
chair
of
mechanics,
he was
awarded
the
chair
of
mathematical
physics
atthe
University
ofRomein 1900.
Volterra
conceived
theideaof a
theory
of
functions
that
depend
ona
continuous
setof
values
of
another
function
in 1883.
Hadamard
was
later
to
introduce
the
word
"functional,"
which
replaced
Volterra's
original
terminology.
In 1890
Volterra
usedhis
functional
calculus
toshow
that
the
theory
of
Hamilton
and
Jacobi
forthe
integration
ofthe
differential
equations
of
dynamics
couldbe
extended
to
other
problems
of
mathematical
physics.
Hismost
famous
work
wasdoneonintegralequations.He
began
this
study
in1884,and
in1896he
published
several
papers
on
what
isnowcalledthe
Volterra
integral
equation.
He
continued
to
study
functional
analysis
applications
to
integral
equations
producing
a
large
number
of
papers
on
composition
and
permutable
functions.
During
the
First
World
War
Volterra
joinedthe Air
Force.
He
made
many
journeys
to
France
and
England
to
promote
scientific
collaboration.
Afterthe
war
he
returned
to
the
University
of
Rome,
and
his
interests
moved
to
mathematical
biology. He
studied
the
Verhulst
equation
andthelogistic
curve.
Healso
wrote
on
predator-prey
equations.
In 1922
Fascism
seized
Italy,
and
Volterra
fought
against
it in the
Italian
Parliament.
However,
by 1930the
Parliament
was
abolished,
andwhen
Volterra
refused
to
take
anoath

ural =
cj
, u'(a) =
C2.
17.1
CLASSIFICATION
491
of allegiance to the
Fascist
government
in 1931,he was
forced
to leavethe
University
of
Rome.
From
thefollowingyearhe livedmostly
abroad,
mainlyin
Paris,
butalso in Spain
and
other
countries.
17.1.3. Example.
Differential
equations
canbe transformed into
integral
equations.
For
instance, considerthe
SOLDE
d
2u
du
dx
2
+Pt
(x)
dx
+
po(x)u
=
r(x),
By
integrating
theDE once,we
obtain
du
LX LX LX
- = - PI
(t)u'
(t)
dt
-
po(t)u(t)
dt
+
ret)
dt +
C2.
dx a a a
Integrating
the
first
integral
by
parts
gives
u'(x)
=
-PI
(x)u(x)
+
LX
[p\
(t)
-
po(t)]u(t)
dt
+
LX
ret)
dt
+PI
(a)ct
+
C2.
~f(X)
~g(X)
III
Neumann
series
solution
Integrating
once moreyields
u(x)
=
-LX
PI
(t)u(t)
dt
+
LX
f(s)
ds +
LX
g(s)ds +(x -
a)[PI
(a)ct
+C2]
=
-LX
PI
(t)u(t)
dt
+
LX
ds l'
[p\
(t)
-
po(t)]u(t)
dt
+
LX
ds l'ret)
dt
+(x -
a)[PI
(a)ct
+C2]+ct
=
LX
(x
-
t)[p\
(t)
- poet)] - PI
(t)}
u(1)
dt
+
LX
(x -
t)r(t)
dt
+(x -
a)[PI
(a)Cj +C2]+cr. (17.6)
where
we haveusedthe
formula
LX
ds l'
f(t)
dt
=
LX
(x -
t)f(t)
dt,
whichthe
reader
mayverifyby
interchanging
the
order
of
integration
ontheLHS.
Equation
(17.6)
isa
Volterra
equation
ofthe
secoud
kind
with
kernel
K(x,
t) sa (x -
t)[p\
(t)
- poet)] - PI (t)
andvex)
'"
f:
(x -
t)r(t)
dt
+(x -
a)[PI
(a)ct
+C2]+ct.
Wenow outline a systematicapproachto obtainingthe infinite seriesof Theo-
rem 17.1.2,which also works for the Fredholmequation of the second kind as we
shallsee in the next section.
In
the latter case, the seriesis guaranteedto converge

492 17.
INTEGRAL
EQUATIONS
only
if
IAIII
KII < 1. This approach has the advantage that in each successive step,
we obtain a better approximation to the solution. Writing the equation as
Iu) = Iv) +AKIu) ,
(17.7)
we can interpret
it as follows. The difference between lu) and [u) is AKlu). If
AK were absent, the two vectors lu) and Iv) would be equal. The effect
of
AK
is to change lu) in such a way that when the result is added to [u), it gives lu).
As our initial approximation, therefore, we take Iu) to be equal to Iv) and write
luo) = [u), where the index reminds us of the order (in this case zeroth, because
AK = 0) ofthe approximation. Tofindabetterapproximation, we always snbstitute
the latest approximation for
lu) in the RHS of Equation (17.7). At this stage, we
have lUI) = Iv) +AKluo) = Iv) +AKIv). Still a betterapproximation is achieved
if we substitute this expression in (17.7):
The procedure is now clear. Once
lu
n),
the
nth
approximation, is obtained, we can
get IUn+l) by substituting in the RHS of (17.7).
Before continuing, let us write the above equations in integral form. In what
follows, we shall concentrate on the Fredhohn equation. To obtain the result for
the Volterraequation, one simply replaces b,the upperlimit of integration, with
x.
The first approximation can be obtained by substituting
v(t)
for
u(t)
on the RHS
of Equation (17.1). This yields
Uj(x)
=
V(X)+A
l
b
K(x,t)v(t)dt.
Substituting this back in Equation (17.1) gives
U2(X) =
v(x)
+Al
b
dsK(x,
s)Uj(s)
=
v(x)
+Al
b
dsK(x,
s)v(s)
+
A21b
dt
[l
b
K(x,
s)K(s,
t)
dS]
v(t)
=
v(x)
+Al
b
dtK(x,
t)v(t)
+
A21b
dtK
2(x,
t)v(t),
where K
2(x,
t) sa
J:
K(x,
s)K(s,
t)ds.
Similar expressions can be derived for
U3(X), U4(X), and so forth. The integrals expressing various "powers" of K can be
obtained
using
Dirac
notation
and
vectors
with
continuous
indices,as discussed
