Hassani S. Mathematical Physics: A Modern Introduction to Its Foundations
Подождите немного. Документ загружается.


15 _
Integral
Transforms
and
Differential
Equations
The discussion in Chapter 14 introduced a general method of solving differential
equations by power series-i-also called the Frobenius
method-which
gives a
solution that converges within a circle
of
convergence. In general, this circle
of
convergence
maybe
small;
however,
thefunction
represented
by thepowerseries
can be analytically continued using methods presented in Chapter
II.
This chapter, which is a bridge between differential equations and operators
on Hilbert spaces (to be developed in the next part), introduces another method
of
solving DEs, which uses integral
transforms
and incorporates the analytic con-
tinuation automatically. The integral transform
of
a function v is another function
u given by
u(z) =
fc
K(z,
t)v(t)dt,
(15.1)
kernel
of
integral
transforms
examples
of
integral
transforms
where C is a convenient contour, and
K(z,
t),
called the
kernel
of the integral
transform, is an appropriate function of two complex variables.
15.0.1.
Example.
Letus consider some examples of
integral
transforms.
(a)TheFouriertransform is
familiar
from
thediscussionof
Chapter
8. The
kernel
is
K(x,
y) = e
ixy.
(b) The
Laplace
transform is used frequently in electrical engineering. Its kernel is
K(x,
y) =
e-
xy.
(c)TheEuler transform hasthekemel
K(x,
y) = (x _ y)v.

434 15.
INTEGRAL
TRANSFORMS
AND
DIFFERENTIAL
EQUATIONS
(d) The Mellintransform has the kernel
st»,
y) =
G(x
Y).
where G is an arbitrary function.
Most
of
the time
K(x,
y) is taken to be simply x
Y.
(e)TheHankel transform has thekernel
K(x,
y) =
yJn(xy),
IIIi
Strategy
for
solving
DEs
using
integral
transforms
where In is the nth-orderBesselfunction.
(f) A transform that is useful in connection with the Bessel equation has the kernel
K(x,y)
=
Gf
e
y-
x'/4y.
The idea behind using integral transform is to write the solution u(z)
of
a DE
in
z in terms
of
an integral such as Equation (15.1) and choose v and the kernel
in such a way as to render the DE more manageable. Let
L
z
be a differential
operator(DO) in the variable z. We want to determine
u(z) suchthat
Ldu]
= 0, or
equivalently, such that
Ie
Lz[K
(z,
t)]v(t)
dt
=
O.
Snppose that we can find
M"
a
DO in the variable
t, such that
LdK(z,
t)l
=
M,[K(z,
t)]. Then the DE becomes
Ie(M,[K(z,
t)]Jv(t)
dt
=
O.
If
C has a and b as initial and final points (a and b
may be equal), then the Lagrange identity [see Equation (13.24)] yields
0=
Lz[u] = t
K(z,
t)M;[V(t)]dt
+
Q[K,
v]I~,
where
Q[K,
v] is the "surface term."
If
vet) and the contour C (or a and b) are
chosen in such a way that
Q[K,
v]l~
= 0
and M;[V(t)]
= 0, (15.2)
the problemis solved. The trickis to find an
M,suchthatEquation(15.2) is easierto
solve thanthe original equation,
L
z
[u] =
O.
Thisin torn demands a cleverchoice
of
the kernel, K(z, t). This chapterdiscusses how to solve some common differential
equations
of
mathematical physics using the general idea presented above.
15.1 IntegralRepresentation ofthe Hypergeometric
Function
Recall that for the hypergeometric function, the differential operator is
d
2
d
L
z
= z(1 - z)dz
2
+[y - (a +
fJ
+
I)zl
dz - afJ
For such
operators-whose
coefficient functions are
polynomials-the
proper
choice for
K(z,
t) is the
Euler
kernel,
(z -
t)'.
Applying L
z
to this kernel and

15.1
INTEGRAL
REPRESENTATION
OF
THE
HYPERGEOMETRIC
FUNCTION
435
rearrmgmgrenns,weO~IDn
Lz[K(z, t)] = /Z2[
-s(s
- 1) -
s(a
+,B
+1) -
a,B]
+
z[s(s-
1) +
sy
+st(a
+,B +1) +2a,Bt] -
yst
- a,BP}(z -
t)'-2.
(15.3)
Notethat exceptfor a multiplicative constant,
Kiz;
t) is synunetric in z
and
t.
This suggests that the general form
of
M,
may
be chosento
be
the same as that
of
L
z
except for the interchange
of
z and t.
If
we
can
manipulate the parameters in
sucha way that
M,becomes simple, then we havea chance
of
solving the problem.
For instance,
if
M, has the form
of
L
z
with
the constant term absent, then the
hypergeometric DE effectively reduces to a
FODE
(in
dv
/
dt).
Let
us exploit this
possibility.
The
general form
of
the M, that we are interested in is
d
2
d
M,
= P2(t)
dt
2
+PI
(t)
dt'
i.e., with no Po term. By applying M, to
K(z,
t) = (z -
t)'
and
setting the result
equal to the RHS
of
Equation (15.3), we obtain
s(s
- 1)p2 - PISZ +
pist
=
Z2[-s(s
- 1) -
s(a
+,B +1) -
a,B]
+ z[s(s - 1) +
sy
+
st(a
+
,B
+1) +2a,Bt]
-
yst
- a,Bt
2,
for which the coefficients
of
equal powers
of
zon
both
sides
must
be
equal:
-
s(s
- 1) -
s(a
+,B +1) - a,B= 0
=}
s =
-a
or s =
-,B,
- PIS =
s(s
- 1) +
sy
+
stt«
+,B +1) +2a,Bt,
s(s
- 1)p2 +pvst =
-yst
- a,Bt
2.
If
we choose s =
-a
(s =
-,B
leads to an equivalent representation), the coeffi-
cient functions
of
M,
will be completely determined.
In
fact, the second equation
gives
PI(t), and the third determines P2(t). We finally obtain
PI(t)
=a+l-y
+t(,B
-a
-1),
and
2 d
2
d
M, = (t - t
)-2
+[a +1 - y +t(,B - a -
1)]-,
dt dt
(15.4)
(15.5)
which, according to Equation (13.20), yields the following DE for the adjoint:
d
2
d
Mi[v] =
-2
[(t - t
2)v]
-
-{[a
- y +1 +t(,B - a - l)]v} =
O.
dt
dt

(15.6)
436 15.
INTEGRAL
TRANSFORMS
AND
DIFFERENTIAL
EQUATIONS
The
solution to this equation is
v(t)
=
Cta-Y(t-
I)Y-~-l
(see
Problem
15.5).
We also
need
the
surface tenm,
Q[K,
v], in the Lagrangeidentity (see
Problem
15.6 for details):
Q[K,
v](t) =
Cat
a-
y+
1(t
-
l)Y-~(z
-
t)-a-l.
Finally, we
need
a specification
of
the
contour.
For
different contours we
will
get differentsolutions.
The
contour
chosen
must,
of
course, have the property that
Q[K,
v] vanishes as a result
of
the
integration.
There
are two possibilities: Either
the
contour
is closed [a = b in (15.2)] or a
i'
b
but
Q[K,
v] takes on the
same
value at a
and
at b.
Let
us
consider
the
second
of
these possibilities. Clearly,
Q[K,
v](t) vanishes
att
= 1
ifRe(y)
> Re(,8). Also, as t
--->
00,
Q[K,
v](l)
--->
(_l)-a-1Cata-y+ltY-~t-a-l
=
(_l)-a-1Cat-~,
which
vanishes
if
Re(,8) >
O.
We thus take a = 1
and
b =
00,
and
assume
that
Re(y)
> Re(,8) >
O.
It
then
follows
that
u(z)
=l
b
K(z,
t)v(t)dt
= c1
00
(t -
z)-ata-
y
(t -
l)y-~-ldt.
The
constaot C' Can be determined to be
r(y)/[r(,8)r(y
- ,8)] (see
Problem
15.7). Therefore,
u(z)
sa
F(a,,8;
y;
z) =
r(,8)~i~)
_ ,8) 1
00
(t -
z)-ata-
y
(t
-l)y-~-ldt.
Euler
formula
for
fhe
hypergeomelric
function
It
is customary to change the variable
of
integration from t to 1/t.
The
resulting
expression is called the
Euler
formula
for
the
hypergeometric function:
F(a
,8'
y'
z) =
r(y)
t(l
-
tz)-at~-l(l-
t)y-~-ldt.
, "
r(,8)r(y
- ,8) 1
0
(15.7)
Note
that
the tenm (1 -
tz)-a
in the integral
has
two
branch
points in
the
z-
plane,
one
at z =
l/t
and
the
other
at z =
00.
Therefore, we
cut
the z-plane
from
Zl =
l/t,
a
point
on the positive
real
axis, to
Z2
=
00.
Since
0
:'0
t
:'0
1, Zl is
somewhere in
the
interval [1,
(0).
To
ensure
that
the
cutis
applicable
for
all values
of
t, we take Zl = 1
and
cut
the
plane
along
the positive
real
axis.
It
follows
that
Equation (15.7) is well behaved as
long
as
o<
arg(l
- z) <
21f.
(15.8)
We
could
choose
a differentcontour,which,in general,
would
lead
to a different
solution.
The
following
example
illustrates
one
such
choice.
15.1.1.Example. Firstnotethat
Q[K,
v]vanishes
att
= Oandt = 1aslongasRe(y) >
Re(li) andRe(a) >
Re(y)
-I.
Hence, wecan choose the contourto start
att
=0 and end

15.2
INTEGRAL
REPRESENTATION
OF
THE
CONFLUENT
HYPERGEOMETRIC
FUNCTION
437
att = 1.Wethenhave
(15.9)
Tosee the
relation
between
w(z) andthe
hypergeometric
function,
expand
(1-
t/z)-a
in
the
integral
to get
w(z) =
e"z-
u
f
r(a
+
n)
(~)n
[I
t
u
+
n-
y
(1 _
tly-P-1dt.
n~O
f(a)r(n
+1) z
Jo
(15.10)
Nowevaluatethe integralby changingt to
l/t
and osing Eqoations(11.19)and (11.17).
Thischangesthe
integral
to
[00
t-u-n-l+P(t
_
l)y-P-
1dt
=
r(a
+n +1 -
y)r(y
- fJ)
Jl
r(a
+n +1 - fJ)
Snbstitnting thisin Equation(15.10), weobtain
c"
-a
~
f(a
+n)f(a
+n
+1-
y)
(1)"
w(z) =
r(a)
r(y
- fJ)z
f;;n
F'(e +n +1-
fJ)r(n
+1) Z
c"
r(a)r(a
+
1-
y)
=
r(a)
f(y
-
fJ)z-a
r(a
+
1-
fJ)
F(a,
a - y +1;a - fJ+1;
l/z),
where
we
have
used
the
hypergeometric
series
of
Chapter
14.
Choosing
e" =
f(a
+1 - fJ)
r(y
-
fJ)r(a
+1 -
y)
yieldsw(z) =
z-a
F(a,
a - y +1;a - fJ+1;
l/z),
whichis oneof the solutions of the
hypergeometric DE [Equation
(14.30)].
II!I
15.2 Integral Representation
of
the Confluent Hy-
pergeometric Function
Having obtained the integral representation
of
the hypergeometric fnnction, we
can readily get the integral representation
of
the conflnent hypergeometric func-
tion by taking the proper limit.
It
was shown in Chapter 14 that
<I>(a,
y; z) =
limp-+oo
F(a,
fJ;
y;
zlfJ).
This snggests taking the limit
of
Equation (15.7). The
presence
of
the ganuna functions with
fJ
as their arguments complicates things,
but on the otherhand, the symmetry
of
the hypergeometric function
can
be utilized

438 15. INTEGRAL
TRANSFORMS
AND
DIFFERENTIAL
EQUATIONS
toour
advantage.
Thus,we may write
<1>(a,
y;
z) = lim F
(a,
fJ;
y;
.:.)
= lim F
(fJ,
a;
y;
.:.)
~
....oo
fJ
~
....
oo
fJ
= lim
r(y)
r
(1-
IZ)-~
1.-
1
(1_
t)y-.-Idl
~
....co
r(a)r(y
-
a)
J
o
fJ
=
<1>(a,
y;
z) =
r(y)
t
eztl·-I(I
_
t)y-.-Idl
r(a)r(y
- a) Jo
(15.11)
becausethe limit
of
the
firsttenn
in the integralis simplye
tz
.Note that the condition
Re(y)
>
Re(a)
> 0 must still hold here.
Integral transforms are particularly useful in determining the asymptotic be-
havior
of
functions. We shall use them in deriving asymptotic formulas for Bessel
functions lateron, and Problem 15.10 derives the asymptotic formula for the con-
fluent hypergeometric function.
15.3 Integral Representation
of
Bessel Functions
Choosing the kernel, the contour, and the function
v(l)
that lead to an integral
representation
of
a function is an art, and the nineteenth century produced many
masters
of
it. A particularly popular theme in such endeavors was the Bessel
equation
and
Bessel
functions.
Thissectionconsiders the
integral
representations
of
Bessel functions.
The
most effective kernel for the Bessel DE is
K(z,
I)
=
Gr
exp
(I
-
~:).
d
Z
I d ( V
Z)
.
When
the Bessel DO L
z
sa
-z
+
--
+
1-
-z
acts on
K(z,
I), it yields
dz z dz z
(
v+1
ZZ)(Z)V
'/4
(d
V+I)
L
K(z,
t) =
---
+I +- - e
t
-
z
t = - -
--
K(z
I).
z I 41
z
2
dt
I '
Thus, M
t
=
df
dt
- (v +
1)/1,
and Equation (13.20) gives
t dv v +I
M
t
[V(I)] =
--
-
--v
= 0,
dt I
whose solution, including the arbitrary constant ofintegrationk, is
v(l)
= ta:":",
Whenwe substitutethis solution and the kernelin the surface term
of
the Lagrange
identity, Equation (13.24), we obtain
Q[K,
V](I) =
PIK(z,
l)v(l)
= k
G)
v
l-
v-I
e
t-
z
' / (4t) .
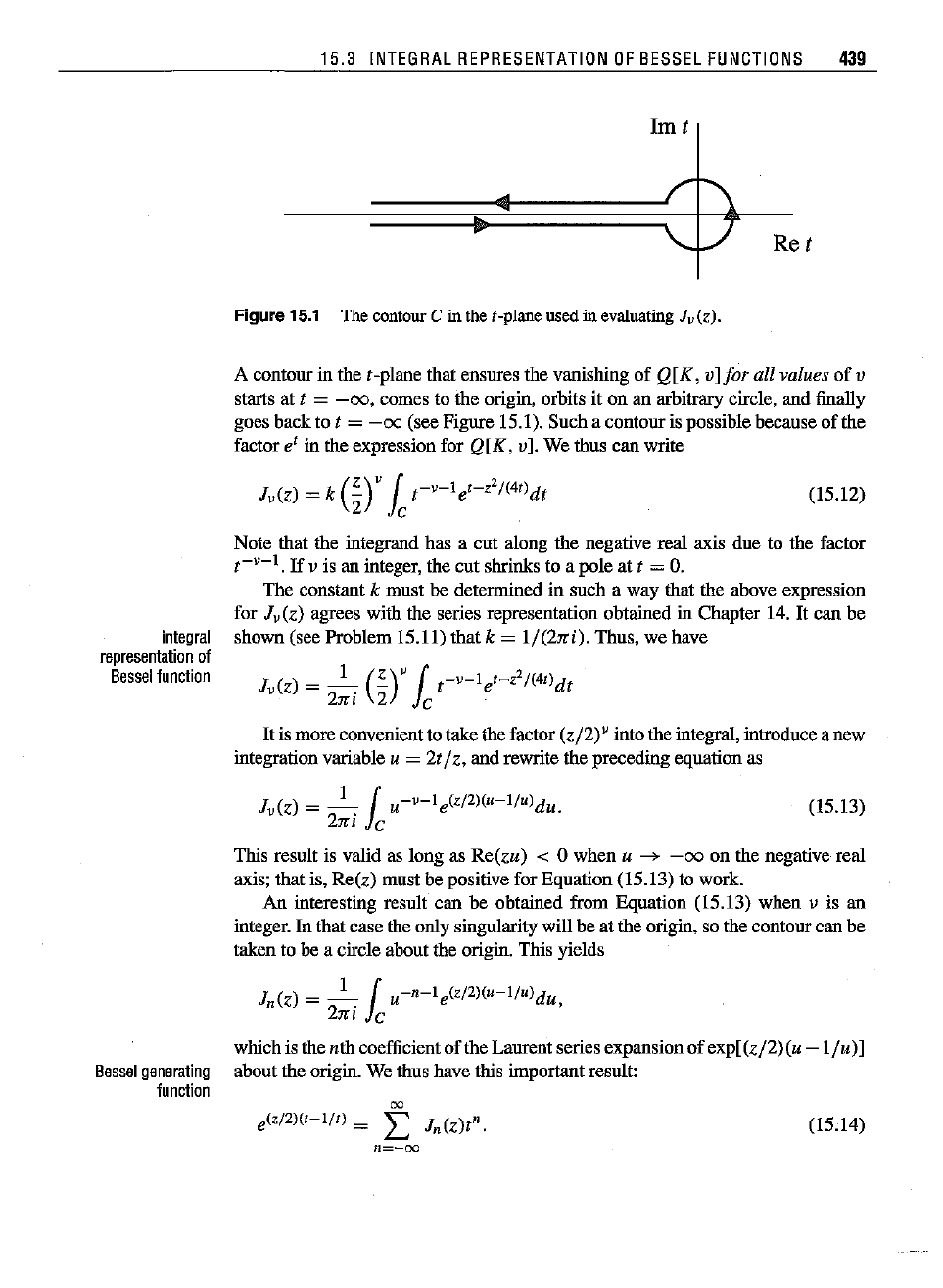
15.3
INTEGRAL
REPRESENTATION
OF
BESSEL
FUNCTIONS
439
Imt
Ret
(15.12)
(15.13)
inlegral
representation
of
Bessel
function
Figure 15.1 ThecontourC in ther-planeusedin evaluating Jv(z).
A contour in the I -plane that ensures the vanishing of Q[K, v]for all values
of
v
starts at I =
-00,
comes to the origin, orbits it on an arbitrary circle, and finally
goes back to
t =
-00
(see Figure 15.1). Such a contour is possible because of the
factor
e
t
in the expression for Q[K, v]. We thus can write
Jv(z) = k
G)
v
fc
t-V-Iet-z2/(4t)dt
Note that the integrand has a cut along the negative real axis due to the factor
I-v-I.
If
v is an integer, the cut shrinks to a pole
att
=
O.
The constant k must be determined in such a way that the above expression
for
Jv(z) agrees with the series representation obtained in Chapter 14. It can be
shown (see Problem 15.11) that
k = 1/(2,,;). Thus, we have
Jv(z) =
~
(~)V
r
t-v-let-z2/(41)dt
2",
2 lc
It
is more convenientto take the factor
(zI2)
vinto the integral, introduce a new
integration variable
u = 2t [z, and rewrite the preceding equation as
Jv(z) =
~
r
u-
v-
1e(z/2)(u-lfu)du.
2",
J
c
This result is valid as long as
Re(zu)
< 0 when u -->
-00
on the negative real
axis; that is,
Re(z)
must be positive for Equation (15.13) to work.
An interesting result can be obtained from Equation (15.13) when v is an
integer.
In
that case the only singularity will be at the origin, so the contour can be
taken to be a circle about the origin. This yields
J (z) = _1_ r
u-
n-
Ie(z/2)(u-lfu)du
n
2ni
Jc
'
which is the nth coefficient of the Laurentseries expansion
of
exp[(zI2)(u
-l/u)]
Bessel
generating
about the origin. We thus have this important resnlt:
function
DO
e(z/2)(t-l/l) = L
In(z)t
n.
n=-oo
(15.14)

(15.15)
440 15.
INTEGRAL
TRANSFORMS
AND
DIFFERENTIAL
EQUATIONS
The
function exp[
(zIZ)
(t - 1
It)
1is therefore appropriately called
the
generating
fnnction
for
Bessel
functions
of
integer
order
(see
also
Problem
14.40).
Equation
(15.14)
can
be usefulin derivingrelations
for
such
Bessel
functionsas
the
following
example shows.
15.3.1.
Example.
Let us rewrite the LHS of (15.14) as eZI/2e-z/21, expand the expo-
nentials,
andcollect
terms
to
obtain
e(z/2)(t-ljt)
=
ezt/2e-z/2t
= f
~
(~)m
f
~
(_~)n
m=Om. 2 n=On. 2t
= f f
(-~)~
(~)m+n
t
m-
n.
m=On=O
m.n.
2
If
we letm - n = k,
change
them
summation
tok, andnote
that
k goes
from
-00
to
00,
we get
e(z/2)(I-I/I) = f f
(_I)n
(~)2n+k
rk
k~-oon~O
(n
+k)!n!
2
00
[(Z)k
00
(_I)n
(Z)2n]
k
k~oo
2:
E
r(n
+k +
l)r(n
+1)
2:
1 .
Comparing
this
equation
with
Equation
(15.14)yieldsthe
familiar
expansion
fortheBessel
function:
(
Z) k
00
(_I)n
(Z)1.
h(z)
=
2:
E
r(n
+k +
l)r(n
+ 1)
2:
.
Wecanalso
obtain
a
recurrence
relation
forI
n
(z),
Differentiating
bothsides
of
Equation
(15.14)with respect to t yields
~
(1
+
k)e(Z/2)(I-I/I)
= f nJn(Z)l
n-
1
n=-oo
UsingEquation (15.14) on the LHS gives
00 00
00
L G+--;)
In(z)t
n
=
~
L
In(z)t
n
+
~
L I
n(z)t
n-
2
n=-oo
2t
n=-oo
n=-oo
00 00
=~
L
In_l(Z)t''-I+~
L I
n+I(Z)I,,-I,
n=-oo n=-oo
(15.16)
where
we
substituted
n - 1forn in the
first
sumandn +1forn inthe
second.
Equating
the
coefficientsof equalpowersof 1onthe LHSandthe RHS ofEquations (15.15) and(15.16),
we get
z
nJn(z)=
2:[J
n-I(Z)
+ J,,+I(Z)],
which was obtainedhy a different method in Chapter 14 [seeEq. (14.48)].
III

15.3
INTEGRAL
REPRESENTATION
OF
BESSEL
FUNCTIONS
441
Imw
Rew
Figure 15.2 ThecontourC' in the w-plane used in evaluatingJvCz).
(15.17)Re(z) > 0,
We can start with Equation (15.13) and obtain other integral representations
of Bessel functions by making appropriate substitutions. For instance, we can let
u =
e"
and assume that the circle of the contour C has unit radius. The contour
C'in thew-plane is
determined
asfollows.
Write
u = rei()
and
w sa x +iy, sol
re
iO
=eXe
iy
yielding r =eXand e
iO
= e
iy.
Along the firstpart
of
C, e=
-rr
and
r goes from
00
to 1.Thus, along the corresponding part of C', y =
-rr
and x goes
from
00
to
O.
On the circular part
of
C, r = 1and egoes from
-rr
to -l-z, Thus,
along the corresponding part of
C', x = 0 and y goes from
-rr
to
+rr.
Finally, on
the last part of C', y = rr and x goes from 0 to
00.
Therefore, the contour C' in
the w-plane is as shown in Figure 15.2.
Substituting
u = e
W
in Equation (15.13) yields
Jv(z) =
---.!:...,
( ezsmhw-vwdw,
21rl
lei
which can be transformed into (see Problem 15.12)
1
In"
sin vrr
In
oo
.
Jv(z) = - cos(ve
-zsine)de
_
--
e-
v
t-
z
sinh
'dt.
n 0 1r 0
(15.18)
integral
representation
of
Bessel
functions
of
integer
order
For the special case
of
integer v, we obtain
I
n
(z) =
~
("
cos(ne - z sin e) de.
rr Jo
In particular,
1
In"
Jo(z) = - cos(z
sine)
de.
rr 0
We can use the integral representation for J
v
(z) to find the integral repre-
sentation for Bessel functions of other kinds. For instance, to obtain the integral
1Do notconfusex andy withtherealand
imaginary
parts
of z,

442 15.
INTEGRAL
TRANSFORMS
AND
DIFFERENTIAL
EQUATIONS
Imw
in
1------1~----
en
Rew
Figure15.3 Thecontourc" in the w-planeusedin evaluating
HS
1
)
(z).
representation for the Neumann function Yv(z), we use Equation (14.44):
1
Yv(z) = (cot V1f)J
v(z)
-
-.--Lv(z)
sm V1r
cot V1l' i
1C
cos VJr
i""
inh
=
__
cos(ve-zsine)de---
e-
Vf
-
z S
"dt
tc 0 7i 0
1
i"
1
i""
.
-.
cos(ve
+zsine)de
_ _ evt-zsinhtdt
tt
smVll' 0
1C
0
with Re(z) >
O.
Substitute tc - e for e in the third integral on the RHS. Then
insertthe resulting integrals plus Equation
(15.18) in HJl) (z) = Jv(z) +iYv(z) to
obtain
Re(z) >
O.
These integrals can easily be shown to result from integrating along the contour
e" of Figure 15.3. Thus, we have
Re(z) >
O.
By changing i to
-t,
we can show that
Re(z)
> 0,
where
e
lll
is the mirror image of
e"
about the real axis.
