Hancock G.J., Murray Th.M., Ellifritt D.S. Cold-Formed Steel Structures to the AISI Specification
Подождите немного. Документ загружается.


Try
P
u
3:65 kips
M
uy
P
u
B ÿ x
cea
5:641 kip-in:
P
Ey
As
ey
34:11 kips
a
y
1 ÿ
P
y
P
Ey
0:893 Eq: C5:2:2-5
P
u
f
c
P
n
C
my
M
uy
f
b
M
ny
a
y
3:65
0:85 25:41
1 5:641
0:90 8:476 0:893
0:997 < 1:0
Eq: C5:2:2-1
P
u
f
c
P
no
M
uy
f
b
M
n
3:65
0:85 39:38
5:641
0:90 8:476
0:849 < 1:0
Eq: C5:2:2-2
Hence, the required axial strength for a load applied
eccentrically at the ¯ange tip is
P
u
3:65 kips
8.5.2 Unlipped Channel Section Beam-Column
Bent About Plane of Symmetry
Problem
Calculate the design axial compressive load in the channel
shown in Figure 7.8, assuming that the channel is loaded
with an axial force on the intersection of the y-axis with one
¯ange. The following section numbers refer to the AISI
Speci®cation.
Solution
A. Elastic Critical Stress for Flexural-Torsional Buckling
due to Bending about Plane of Symmetry
Chapter 8
238

Section C3.1.2.1 (1999 Supplement No. 1)
C
b
1:0 uniform moment
S
f
I
x
D=2
2:038 in:
3
F
e
C
b
Ar
0
S
f
s
ey
s
t
p
48:2 ksi Eq: C3:1:2:1-5
Since 2:78F
y
> F
e
> 0:56F
y
,
F
c
10
9
F
y
1 ÿ
10F
y
36F
e
31:67 ksi Eq: C3:1:2:1-3
B. Effective Section Modulus (S
cx
) and Nominal Flexural
Strength (M
nx
) at a Stress F
c
For the loading eccentricity causing uniform compres-
sion on the top ¯ange and bending in the web as shown in
Figure 8.7, the effective widths of the compression ¯ange
under bending need to be calculated.
Section B3.1 applied to compression ¯ange of channel
k 0:43 f F
c
l
1:052
k
p
w
t
f
E
r
0:736 Eq: B2:1-4
r
1 ÿ 0:22=l
l
0:953 Eq: B2:1-3
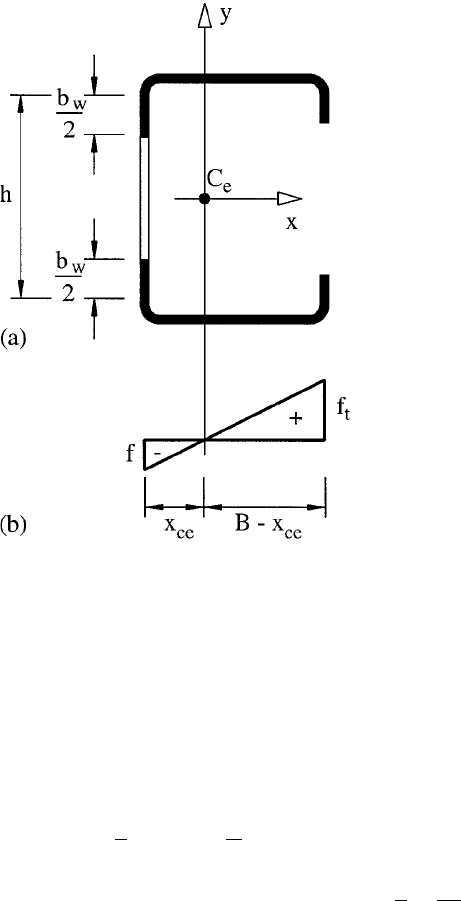
FIGURE 8.7 Effective section for bending about axis of symmetry.
Members in Combined Axial Load and Bending
239

Since l > 0:679, then
b
f
rw 1:667 in: Eq:B2:1-2
A
e
tw b
f
h 2u1:188 in:
2
y
ce
t
2
b
f
ut R ÿ c
D
2
h
uD ÿ t ÿ R cwDÿ
t
2
t
A
e
3:026 in:
I
xe
t
2
2
b
f
ut R ÿ c
2
D
2
2
h
"
uD ÿ t ÿ R c
2
wDÿ
t
2
2
#
t
t
h
3
12
ÿ A
e
y
2
ce
6:024 in:
4
S
cx
I
xe
y
ce
1:991 in:
3
M
nx
S
cx
F
c
63:05 kip-in:
C. Combined Axial Compressive Load and Bending
Section C5 For uniform moment
C
mx
C
m
1:0
Section C5.2.1 ASD method
O
c
1:80 O
b
1:67
Try
P 6:6 kips
M
x
PD
2
19:8 kip-in:
A 1:199 in:
2
Example 7:6:2
s
ex
412:6 ksi
P
Ex
As
ex
494:5 kips
a
x
1 ÿ
O
c
P
P
Ex
0:976 Eq: C5:2:1-4
Chapter 8
240

O
c
P
P
n
O
b
C
mx
M
x
M
nx
a
x
1:80 6:6
25:41
1:67 1 19:8
63:05 0:976
1:00
Eq: C5:2:1-1
O
c
P
P
no
O
b
M
x
M
nx
1:80 6:6
39:38
1:67 19:8
63:05
0:83
Eq: C5:2:1-2
Hence, the nominal axial compressive load applied eccen-
trically on one ¯ange is
P 6:6 kips
Section C5.2.2 LRFD method
f
c
0:85 f
b
0:90
Try
P
u
9:9 kips
M
ux
P
u
D
2
29:7 kip-in:
P
Ex
As
ex
494:5 kips
a
x
1 ÿ
P
u
P
Ex
0:980 Eq: C5:2:2-5
P
u
f
c
P
n
C
mx
M
ux
f
b
M
nx
a
x
9:9
0:85 25:41
1 29:7
0:90 63:05 0:98
0:992 < 1:0 Eq: C5:2:2-1
P
u
f
c
P
no
M
ux
f
b
M
nx
9:9
0:85 39:38
29:7
0:90 63:05
0:819 < 1:0 Eq: C5:2:2-2
Hence, the required axial strength for a load applied
eccentrically on one ¯ange is
P
u
9:9 kips
Members in Combined Axial Load and Bending
241
8.5.3 Lipped Channel Section Beam-Column
Bent in Plane of Symmetry
Problem
Calculate the design axial compressive load in the lipped
channel shown in Figure 7.9, assuming that the channel is
loaded with an axial force on the intersection of the x-axis
with the web outer edge. The following section numbers
refer to the AISI Speci®cation.
Solution
A. Section Property ( j ) for Torsional-Flexural Buckling
From Figure 7.9b and Example 7.6.3,
a 3:94 in: b 2:94 in: c 0:595 in:
t 0:60 in:
m
s
b3a
2
b c6a
2
ÿ 8c
2
a
3
6a
2
b c8c
2
ÿ 12ac 6a
2
1:493 in:
x
bb 2c
a 2b 2c
1:103 in:
x
os
ÿm
s
ÿ
x 2:596 in:
I
ys
2b
3
t
12
2bt
b
2
ÿ
x
2
at
x
2
2ctb ÿ
x
2
0:83 in:
4
Note that the distances x
os
and
x and the value of I
ys
have all
been computed for the square corner model in Figure 7.9b.
b
w
ÿ
t
xa
3
12
ÿ t
x
3
a ÿ0:654 in:
5
b
f
1
2
tb ÿ
x
4
ÿ
x
4
1
4
a
2
tb ÿ
x
2
ÿ
x
2
0:80 in:
5
b
1
2ctb ÿ
x
3
2
3
tb ÿ
x
a
2
3
ÿ
a
2
ÿ c
3
0:814 in:
5
j
b
w
b
f
b
1
2I
ys
ÿ x
os
3:174 in:
Chapter 8
242

B. Elastic Critical Stress for Torsional-Flexural Buckling
due to Bending in Plane of Symmetry
Section C3.1.2.1 (1999 Supplement No. 1)
Use s
ex
, s
t
, r
0
from Example 7.6.3: s
ex
127:9 ksi,
s
t
78:89 ksi, r
0
3:28 in.
C
s
1 compression on shear center side of
centroid
C
TF
1:0 uniform moment
S
f
I
y
x
c
0:705 in:
2
F
e
C
s
As
ex
j C
s
j
2
r
2
0
s
t
=s
ex
q
hi
C
TF
S
f
849 ksi
Since F
e
5 2:78F
y
, then
F
c
F
y
45 ksi Eq: C3:1:2:1-2
C. Effective Section Modulus (S
cy
) and Nominal Flexural
Strength (M
ny
) at a Stress F
c
For the loading eccentricity causing tension in the
lips and compression in the web under the bending com-
ponent, the effective widths of the ¯anges under bending
may need to be calculated. First the effective width of the
web is calculated in compression. The section is shown in
Figure 8.8.
Section B2.1 applied to web of channel
k 4:0 f F
c
l
1:052
k
p
w
t
f
E
r
1:243 Eq: B2:1-4
r
1 ÿ 0:22=l
l
0:662 Eq: B2:1-3
Members in Combined Axial Load and Bending
243
Since l > 0:673, then
b
w
rh 2:404 in: Eq:B2:1-2
A
e
t2w b
w
4u 2d0:571 in:
2
x
ce
t
2
b
w
2w
B
2
2ut R ÿ c
2uB ÿ R ÿ t c2dBÿ
t
2
t
A
e
1:265 in:
FIGURE 8.8 Effective section for bending in plane of symmetry
(web in compression): (a) effective section; (b) bending stresses.
Chapter 8
244

Since the ¯anges are fairly stocky when treated as webs in
bending, they will be fully effective and their effective
widths in bending do not need to be calculated.
I
ye
t
2
2
b
w
2w
B
2
2
2ut R ÿ c
2
"
2uB ÿ R ÿ t c
2
2dBÿ
t
2
2
#
t
2t
w
3
12
ÿ A
e
x
2
ce
0:693 in:
4
S
cy
I
ye
x
ce
0:548 in:
3
M
ny
S
cy
F
c
24:65 kip-in: Eq: C3:1:2-1
The moment M
ny
may be greater than the nominal section
¯exural strength M
no
since it is based on the effective
section modulus for the compression ¯ange at a stress F
c
as stated in Section C3.1.2. The nominal section ¯exural
strength for the tension ¯ange at yield also needs to be
calculated.
Assume a stress in the compression ¯ange which will
produce yield in the tension ¯ange and iterate until the
tension ¯ange is at yield as shown in Figure 8.8. Assume
f 30:8 ksi.
k 4:0
l
1:052
k
p
h
t
f
E
r
1:028 Eq: B2:1-4
r
1 ÿ 0:22=l
l
0:764 Eq: B2:1-3
Members in Combined Axial Load and Bending
245
Since l > 0:673, then
b
w
rh 2:775 in: Eq: B2:1-2
A
e
t2w b
w
4u 2d0:593 in:
2
x
ce
t
2
b
w
2w
B
2
2ut R ÿ c
2uB ÿ R ÿ t c2dBÿ
t
2
t
A
e
1:218 in:
f
t
f
B ÿ x
ce
x
ce
45:0 ksi
Hence, tension ¯ange is at yield and compression ¯ange is
at a stress lower than yield.
Since the ¯anges are fairly stocky when treated as
webs in bending, they will be fully effective and their
effective widths in bending do not need to be calculated.
I
ye
t
2
2
b
w
2w
B
2
2
2ut R ÿ c
2
"
2uB ÿ R ÿ t c
2
2dBÿ
t
2
2
#
t
2t
w
3
12
ÿ A
e
x
2
ce
0:725 in:
4
S
ey
I
ye
B ÿ x
ce
0:407 in:
3
M
no
S
ey
F
y
18:32 kip-in: Eq: C3:1:1-1
This value of M
no
is less than M
ny
24:65 kip-in. computed
above since the tension ¯ange is at yield. Hence,
M
ny
M
no
18:32 kip-in:
Chapter 8
246
D. Combined Axial Compressive Load and Bending
Section C5.2 For uniform moment
C
my
C
m
1:0
Centroid of effective section under axial force alone from
Section 7.6.3D:
x
cea
0:958 in:
Use P
no
, P
n
from Example 7.6.3: P
no
19:74 kips, P
n
15:75 kips.
Clause C5.2.1 ASD method
O
c
1:80 O
b
1:67
Try
P 4:8 kips
M
y
Px
cea
4:60 kip-in:
A 0:645 in:
2
Example 7:6:3
s
ey
223:6 ksi
P
Ey
As
ey
144:1 kips
a
y
1 ÿ
O
b
P
P
Ey
0:940 Eq: C5:2:1-5
O
c
P
P
n
O
b
C
my
M
y
M
ny
a
y
1:80 4:8
15:75
1:67 1 4:60
18:32 0:940
1:0
Eq: C5:2:1-1
O
c
P
P
no
O
b
M
y
M
ny
1:80 4:8
19:74
1:67 4:60
18:32
0:857
Eq: C5:2:1-2
Hence, the nominal axial compressive load applied eccen-
trically at web is
P 4:8 kips
Section C5.2.2 LRFD method
f
c
0:85 f
b
0:90
Members in Combined Axial Load and Bending
247
