Hammond C. The Basics of Crystallography and Diffraction

Подождите немного. Документ загружается.

154 The reciprocal lattice

101

002

001

102

(100)

(001)

(002)

(001)

(101)

(102)

002

001

000

001

101

100

(101)

101

(a) (b) (c)

101

102

100

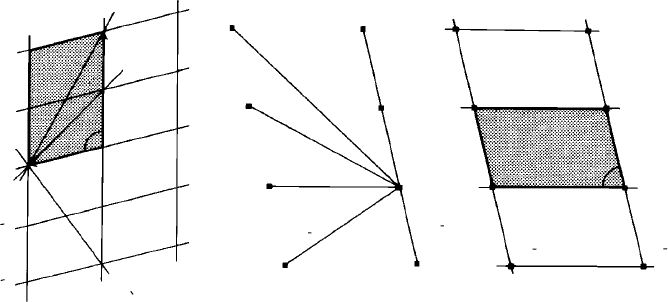
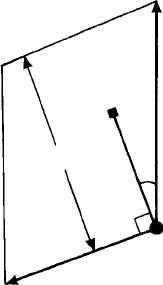
Fig. 6.4. (a) Plan of a monoclinic P unit cell perpendicular to the y-axis with the unit cell shaded. The

traces of some planes of type {h0l} (i.e. parallel to the y-axis) are indicated, (b) the reciprocal (lattice)

vectors, d

∗

hkl

for these planes and (c) the reciprocal lattice deﬁned by these vectors. Each reciprocal

lattice point is labelled with the indices of the plane it represents and the unit cell is shaded. The angle

∗

is the complement of β.

(i.e. containing the a and c lattice vectors) from which we will ﬁnd the reciprocal lattice

unit cell vectors a

∗

and c

∗

. This then enables us to express reciprocal lattice vectors in

this section in terms of their components on these unit cell vectors. It is then a simple

step to extend these ideas to three dimensions.

Figure 6.4(a) shows a section of a monoclinic P lattice through the origin and per-

pendicular to the y-axis or b unit cell vector. The section of the unit cell is outlined by

the lattice vectors a and c at the obtuse angle β and also the traces of some planes of the

type (h0l) (i.e. those planes parallel to the y-axis). In Fig. 6.4(a), (and Fig. 6.7(a)) no

distinction is made between Miller indices and Laue indices—the indices of the planes

are all put in brackets whether or not they all pass through lattice points.

Figures 6.4(b) and (c) show the reciprocal lattice vectors for these planes constructed

in the same way as before (Section 6.2), with the reciprocal lattice points labelled with

the index of the planes they represent. Note again the reciprocal relationships between

the lengths of the vectors and the d

hkl

-spacings, e.g. the (002) planes with half the d -

spacing of the (001) planes are represented by a reciprocal lattice point 002, twice the

distance from the origin as the reciprocal lattice point 001. Obviously, 003 will be three

times the distance, and so on.

It can be seen that the reciprocal lattice points (the ‘end points’ of the reciprocal

lattice vectors) do indeed form a grid or lattice—hence the name. This is emphasized in

Fig. 6.4(c), which also shows the reciprocal lattice unit cell for this section outlined by

reciprocal lattice unit cell vectors a

∗

and c

∗

, where

∗

= d

∗

100

and |a

∗

|=1/d

100

; c

∗

= d

∗

001

and |c

∗

|=1/d

001

6.3 Reciprocal lattice unit cells 155

102

002

001

000

101

100

102

002

102

112

012

112

011

111

110

111

112

111

011

010

110

012

111

(a) section

h0l

(b) section

h1l

101

100

101

102

001

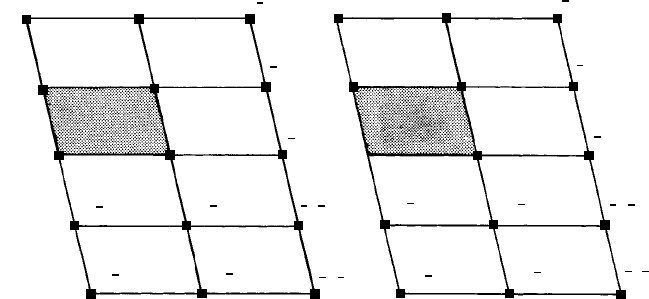
Fig. 6.5. Sections of a monoclinic reciprocal lattice perpendicular to the b

∗

vector or y

∗

-axis, (a) h0l

section through the origin 000, built up by simply extending the section in Fig. 6.4(c); (b) h1l section

(representing planes intersecting the y-axis at one lattice vector b) ‘one layer up’ along the b

∗

axis.

Note that a

∗

and c

∗

are not parallel to a and c, respectively, because the normals to the

(100) and (001) planes in the monoclinic lattice are not parallel to a and c, respectively.

Also the angle β

∗

between a

∗

and c

∗

is the complement of the angle β.

Figure 6.4(c) shows just part of the reciprocal lattice for the few planes we have

labelled in Fig. 6.4(a). It can obviously be extended for many more planes and the

reciprocal lattice points labelled by adding indices like coordinates, as is shown in

Fig. 6.5(a), with the origin labelled 000.

These ideas are readily extended to the third dimension; the b

∗

vector is perpendicular

to the plane of the paper, normal to the (010) planes which are parallel to the plane

of the paper, i.e. in the monoclinic system b is parallel to b

∗

and the 010 reciprocal

lattice point is ‘one step above’ 000 out of the plane of the paper. Similarly with all

the other reciprocal lattice points whose k index is 1; the 011 reciprocal lattice point

is ‘one step above’ 001 and so on. All these points form another layer, or section of

the reciprocal lattice as shown in Fig. 6.5(b). Obviously we can build up as many

sections of the reciprocal lattice, representing as many planes in the crystal, as we

please; the ‘ground ﬂoor’ layer containing the h0l reciprocal lattice points, the section

one step along the b axis (the ‘ﬁrst ﬂoor’layer) containing the h1l reciprocal lattice points

and so on.

Now, before expressing these ideas in vector notation, we can reﬂect on what we have

already achieved. First, we are able to represent any set of planes in a crystal by a single

reciprocal lattice point: consider how difﬁcult and confusing it would be to have to draw

very many different planes in crystal in the same way as in Figs 5.2 or 5.3! Second,

the indices (strictly the Laue indices since they have common factors) are represented

simply as coordinates of reciprocal lattice points.

156 The reciprocal lattice

111

011

101

110

100

010

000

001

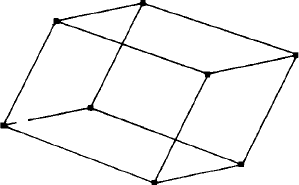
Fig. 6.6. The reciprocal lattice unit cell of a monoclinic P crystal deﬁned by reciprocal lattice vectors

∗

, b

∗

and c

∗

. β

∗

is the angle between a

∗

and c

∗

In vector notation, the reciprocal lattice vectors can now be expressed in terms of

their components of the reciprocal unit cell vectors a

∗

, b

∗

, c

∗

. For example, for the

(102) family of planes (Figs 6.4(b) and (c)) d

∗

102

= 1a

∗

+ 0b

∗

+ 2c

∗

, or, in general,

∗

hkl

= ha

∗

+ kb

∗

+ lc

∗

Hence, just as direction symbols [uvw] are the components of a vector r

uvw

in direct space

(Section 5.2), so also plane indicesare the components of avector d

∗

hkl

in reciprocalspace.

It is worth while rewriting these two equations once again to emphasize their

importance and what might be called their symmetry:

uvw

= ua + vb + wc

(direction symbols are simply the components of a direct lattice vector)

∗

hkl

= ha

∗

+ kb

∗

+ lc

∗

(Laue indices are simply the components of a reciprocal lattice vector).

The reciprocal lattice unit cell of the monoclinic crystal is drawn in Fig. 6.6 in an

orientation where the a

∗

, b

∗

and c

∗

unit cell vectors and the reciprocal lattice points

at the corners can be seen clearly. Notice that the idea of ‘layers’ of reciprocal lattice

points applies (of course) to all orientations, for example the ‘bottom face’ of the cell

contains the hk0 reciprocal lattice points, the ‘top face’, one step along c

∗

contains the

hk1 reciprocal lattice points—and so on.

6.4 R eciprocal lattice cells for cubic crystals

In crystals with orthogonal axes (cubic, tetragonal, orthorhombic) the reciprocal lattice

vectors a

∗

, b

∗

, c

∗

are parallel to a, b, c, respectively. Hence we have the further identities

that a ·b = 0, a

∗

· b = 0, etc. The reciprocal lattice unit cell of a simple cubic crystal

(cubic P lattice) is obviously a cube with reciprocal lattice points only at the corners. The

reciprocal unit cells of the cubic I and cubic F lattices also have additional lattice points

6.4 Reciprocal lattice cells for cubic crystals 157

110

000 020 040

130

240220

200

400

(211)

(200)

(110)

(020)

(a) (b)

420 440

310 330

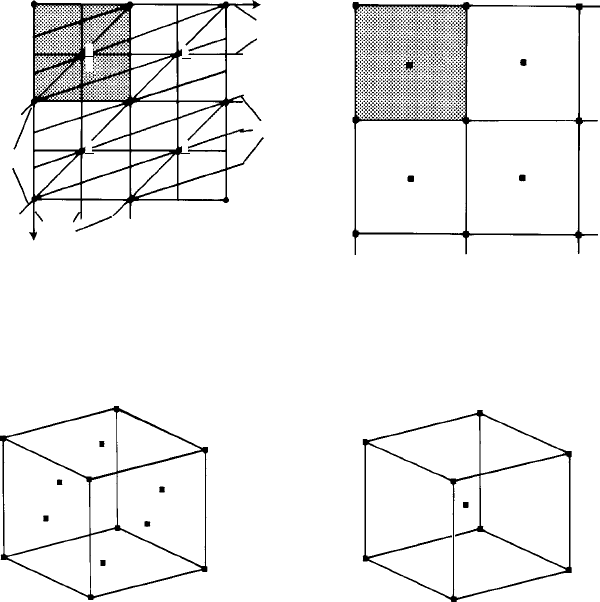
Fig. 6.7. (a) Plan of a cubic I crystal perpendicular to the z-axis and (b) pattern of reciprocal lattice

points perpendicular to the z-axis. Note the cubic F arrangement of reciprocal lattice points in this plane.

002

022

222

202

111

020

220

200

000

022

222

220

200

(a) (b)

000

002

112

202

121

211

020

110

101

011

Fig. 6.8. (a) The cubic F reciprocal lattice unit cell of the cubic I (direct) lattice; (b) The cubic I

reciprocal lattice cell of the cubic F (direct) lattice.

within the unit cells, i.e. they are also not primitive. This is illustrated for the case of the

cubic I lattice in Fig. 6.7, which shows four unit cells with the z-axis perpendicular to the

plane of the paper and the traces of several hk0 planes (parallel to the z-axis) sketched

in. Notice (for example) that in the direction of the x-axis the ﬁrst set of lattice planes

encountered is not (100) but (200) because of the presence of the additional lattice points

in the centres of the cells (see also Fig. 5.4). Hence the reciprocal lattice vector in this

direction is equal to d

∗

200

not d

∗

100

; similarly, in the direction of the y-axis it is d

∗

020

.In

the [110] direction, however, the ﬁrst set of lattice planes encountered is (110), which

gives a reciprocal lattice point in the centre of the face of the cell and the second-order

220 reciprocal lattice point at the corner. Proceeding in this way we ﬁnd that this section

of the reciprocal lattice is face-centred. Repeating this procedure in the other sections

gives a face-centred cubic reciprocal lattice (cubic F ) (Fig. 6.8(a)) for the body-

centred cubic (direct) lattic (cubic I )—the two are reciprocally related. In the same

158 The reciprocal lattice

way, we ﬁnd that the reciprocal lattice of the face-centred cubic lattice is body-centred

(Fig. 6.8(b)).

There is another way of looking at these reciprocal relationships. Recall that the cubic

lattices may all be referred to rhombohedral axes (primitive cells) with axial angles at 60

◦

(cubic F), 90

◦

(cubic P), and 109.47

◦

(cubic I ) (Section 3.2, Fig. 3.2). The reciprocals

of these cells are again rhombohedral cells with axial angles 109.47

◦

(i.e. cubic I ), 90

◦

(i.e. cubic P) and 60

◦

(i.e. cubic F), respectively.

Finally, just as we can deﬁne the environments around lattice points in terms of

Voronoi polyhedra, or Wigner–Seitz cells (Section 3.4), so also can we deﬁne the envi-

ronments around reciprocal lattice points in just the same way and in this case the

polyhedra are called Brillouin zones. Brillouin zones are useful in describing the energy

states of electrons in metallic crystals. For a cubic F crystal, for which the reciprocal

lattice is cubic I , the ﬁrst Brillouin zone is a truncated octahedron and for a cubic I

crystal, for which the reciprocal lattice is cubic F, it is a rhombic dodecahedron (see

Fig. 3.7(d) and (e) and Appendix 2).

6.5 Proofs of some geometrical relationships

using reciprocal lattice vectors

Some useful geometrical relationships stated without proof in Chapter 5 can be proved

very simply using the concept of the reciprocal lattice and an elementary knowledge of

vector algebra (see Appendix 5). The results are summarized in Appendix 4.

6.5.1 Relationships between a, b, c and a

∗

, b

∗

, c

∗

Consider, for example, c

∗

(Fig. 6.4) and its relationships with a, b and c, which are

redrawn for clarity in Fig. 6.9. showing in addition the angle φ between c and c

∗

001

Fig. 6.9. Plan of a monoclinic unit cell perpendicular to the y-axis emphasizing the geometrical

relationships between a, c and c

∗

(see Fig. 6.4 and Section 6.5.1).

6.5 Proofs of some geometrical relationships 159

Since c

∗

is perpendicular to both a and b, the scalar (or dot) products are zero, i.e.

∗

· a = 0, c

∗

· b = 0 and similarly for a

∗

and b

∗

, i.e. a

∗

· b = 0, a

∗

· c = 0, b

∗

· a =

0, b

∗

· c = 0.

Now consider the scalar product c · c

∗

= c|c

∗

|cos φ. However, since |c

∗

|=1/d

001

by deﬁnition and c cos φ = d

001

, then c · c

∗

= d

001

= 1 and similarly for a · a

∗

= 1

and b · b

∗

= 1.

6.5.2 The addition rule

This rule is simply based on the addition of reciprocal lattice vectors. For example (Fig.

6.4(b)), d

∗

102

= d

∗

101

+ d

∗

001

or, in general,

∗

(mh

+nh

)(mk

+nk

)(ml

+ml

)

= d

∗

m(h

)

+ d

∗

n(h

)

6.5.3 The Weiss zone law or zone equation

If a plane (hkl) lies in a zone [uvw], then d

∗

hkl

is perpendicular to r

uvw

, i.e. d

∗

hkl

·r

∗

uvw

= 0

Writing d

∗

hkl

and r

uvw

in terms of their components,

(ha

∗

+ kb

∗

+ lc

∗

) · (ua + vb + wc) = 0

Hence

hu +ku + lw = 0 because a

∗

· a = 1, a

∗

· b = 0, etc.

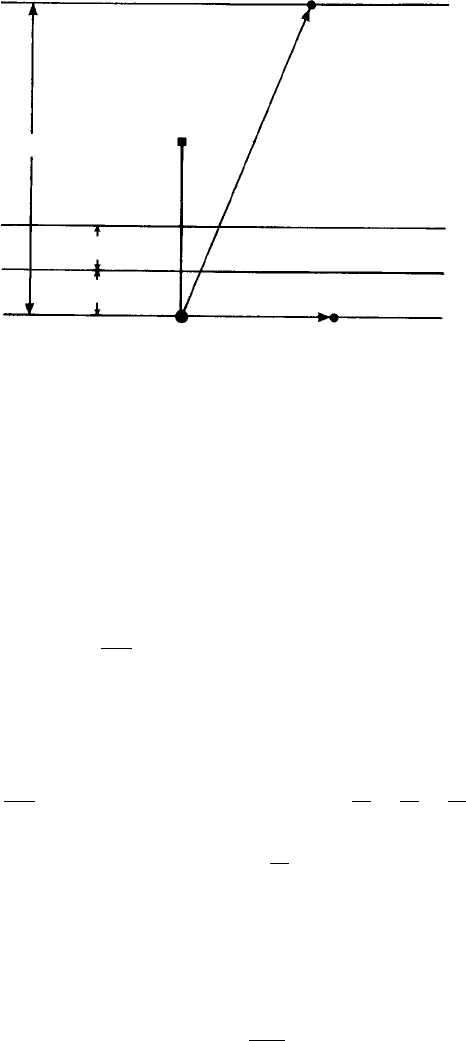
The zone law can be generalized as follows. Consider the condition for a lattice

point with coordinates uvw (or with position vector r

uvw

) to lie in a lattice plane (hkl)

(Fig. 6.10). For the lattice plane passing through the origin, r

uvw

is perpendicular to d

∗

hkl

and hence hu + kv + lw = 0 as before. Now consider the nth lattice plane which lies at

a perpendicular distance nd

hkl

from the origin.

The condition for a lattice point to be in this plane is that the component of r

uvw

perpendicular to the planes should equal this distance; i.e. r

uvw

· i = nd

hkl

where i is a

unit vector perpendicular to the planes. Now, since by deﬁnition

i =

∗

hkl

∗

hkl

= d

∗

hkl

then

uvw

· d

∗

hkl

= nd

hkl

;

hence

uvw

· d

∗

hkl

= n

and, substituting for r

uvw

and d

∗

hkl

as before,

hu +ku + lw = n.

160 The reciprocal lattice

lattice point on

plane through the

origin

lattice point nth

plane from the origin

O(origin)

hkl

uvw

Fig. 6.10. Diagram representing the geometry of the (generalized) zone law. A set of hkl planes are

drawn ‘edge on’. When a lattice point uvw lies on a plane through the origin then hu + ku + lw = 0;

when a lattice point lies on the nth plane from the origin then hu +kv +lw = n.

6.5.4 d-spacing of lattice planes (hkl)

Recalling (Appendix 5) that the scalar product of a vector multiplied by itself is the

modulus squared:

∗

hkl

· d

∗

hkl

= (ha

∗

+ kb

∗

+ lc

∗

) · (ha

∗

+ kb

∗

+ lc

∗

Simple expressions are onlyobtained for crystals with orthogonal axes (orthorhombic,

tetragonal, cubic) where a

∗

· b

∗

= 0, etc., i.e. for orthorhombic crystals;

hkl

= ha

∗

· ha

∗

+ kb

∗

· kb

∗

+ lc

∗

· lc

∗

since a

∗

· a

∗

, etc.

6.5.5 Angle ρ between plane normals (h

) and (h

)

The angle ρ between two vectors a and b is given by (Appendix 5):

cos ρ =

a · b

6.6 Lattice planes and reciprocal lattice planes 161

Hence:

cos ρ =

∗

· d

∗

||d

∗

Again, substituting in terms of components gives a simple expression only for cubic

crystals.

6.5.6 Deﬁnition of a

∗

, b

∗

, c

∗

in terms of a, b, c

The volume of the unit cell V is given by a ·(b × c) (see Appendix 5). Now, as (b ×c)

is a vector parallel to a

∗

and of modulus equal to the area of the face of the unit cell

deﬁned by b and c, then a

∗

= (b ×c)/V = (b ×c)/a ·(b ×c), and similarly for b

∗

and

∗

. a, b and c can be deﬁned in the same way, i.e. a = (b

∗

× c

∗

)/V

∗

, and similarly for

b and c, where V

∗

is the volume of the reciprocal unit cell.

Hence to summarize:

∗

b × c

, b

∗

c × a

∗

a × b

a =

∗

× c

∗

, b =

∗

× a

∗

c =

∗

× b

∗

6.5.7 Zone axis at intersection of planes (h

) and (h

)

The zone axis is deﬁned by r

uvw

, the vector product of

∗

and d

∗

Substituting in terms of their components and remembering the identities a = (b

∗

)/V

∗

, etc., gives

ua + vb + wc = a(k

− k

) + b(l

− l

) + c(h

− h

)

therefore (see Memogram, Section 5.6.2)

u = (k

− k

); v = (l

− l

); w = (h

− h

6.5.8 A plane containing two directions [u

] and [u

]

The plane is deﬁned by d

∗

hkl

, the vector product of r

and r

. Proceeding as

above gives (see Memogram, Section 5.6.3)

h = (v

− v

); k = (w

− w

); l = (u

− u

6.6 Lattice planes and reciprocal lattice planes

Just as we have lattice planes passing through lattice points in the ‘direct’ lattice, so

also we have planes (or layers) passing through reciprocal lattice points in the reciprocal

162 The reciprocal lattice

lattice. There is, as far as I know, no standard terminology to describe these reciprocal

lattice planes or layers nor their spacings (unlike the familiar (hkl) and d

hkl

for lattice

planes) so I will call them (uvw)

∗

reciprocal lattice planes with spacing r

∗

uvw

—the stars

to indicate that they are planes and spacings in reciprocal space. In the case of X-

ray diffraction, the reciprocal lattice planes correspond to the layer-lines of spots in

oscillation photographs (Fig. 9.17) and in the case of electron diffraction they are called

Laue zones—the plane or layer of reciprocal lattice points passing through the origin

being called the zero order Laue zone; the next plane or layer ‘up’ from the origin being

called the ﬁrst order Laue zone, and so on (Fig. 11.1).

The spacings r

∗

uvw

of reciprocal lattice planes are deﬁned in a precisely analogous way

to that for the spacings of lattice planes, d

hkl

, so we will write the equations side-by-side

to emphasise their ‘symmetry’:

∗

uvw

ua + vb + wc

hkl



∗

hkl



∗

+ kb

∗

+ lc

∗

In short, just as lattice planes (hkl) are, by deﬁnition, perpendicular to the reciprocal

lattice vector d

∗

hkl

and of reciprocal spacing, so also are reciprocal lattice planes (uvw )

∗

perpendicular to the direct lattice vector r

uvw

and of reciprocal spacing.

These interrelationshipsare perhaps best understoodby means ofaparticular example.

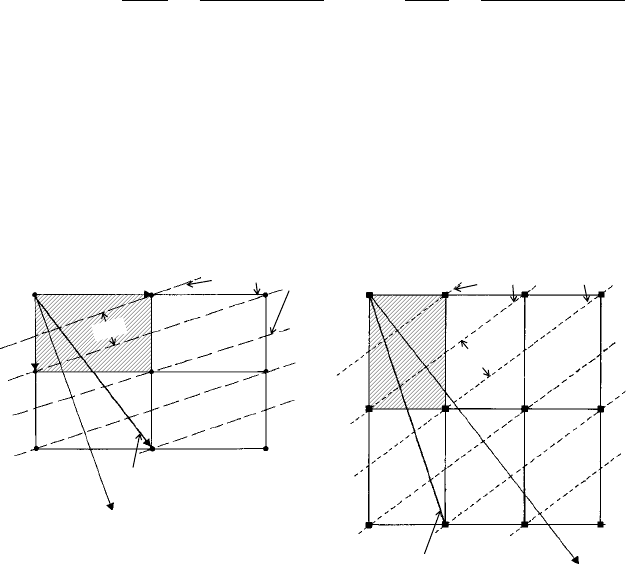
Figure 6.11(a) shows a plan view (perpendicular to the c-axis) of an orthorhombic crystal.

The unit cell, lightly shaded, is outlined by lattice vectors a and b. The traces of a

particular set of lattice planes, (210), are indicated by the long dashed lines together

lattice planes (210)

reciprocal lattice planes (210)

000 010 020 030

100 110 120 130

200 210

(a) (b)

220 230

210

= 2a + 1b + 0c

210

= 2a

+ 1b

+ 0c

normal to (210) planes

and parallel to d

210

normal to (210)

reciprocal lattice planes

and parallel to r

210

Fig. 6.11. (a) The (direct) lattice of a simple (primitive) orthorhombic crystal with the unit cell shaded,

traces of the (210) lattice planes (long dashed lines) and their normal and the lattice vector r

210

. (b) The

corresponding reciprocal lattice with the unit cell shaded, traces of the (210)

∗

reciprocal lattice planes

or layers (short dashed lines) and their normal (parallel to r

210

) and the reciprocal lattice vector d

∗

210

(parallel to the normal to the lattice planes 210).

6.7 Summary 163

with their normal and also the lattice vector r

210

= (2a +1b +0c). Note that the normal

to the lattice planes is not parallel to the direction [210] (see Fig. 5.5).

Figure 6.11(b) shows the corresponding plan view of the reciprocal orthorhombic

lattice, the unit cell, lightly shaded, being outlined by reciprocal lattice vectors a

∗

and

∗

. (In this case, (orthogonal axes) a

∗

is parallel to a and b

∗

is parallel to b.) The traces

of the reciprocal lattice planes (210)

∗

are indicated by the short dashed lines together

with their normal and also the reciprocal lattice vector d

∗

210

= (2a

∗

+ 1b

∗

+ 0c

∗

Note, by comparing the diagrams, that d

∗

210

is (by deﬁnition) perpendicular to the lattice

planes (210) and that r

210

is also (by deﬁnition) perpendicular to the reciprocal lattice

planes (210)

∗

The Weiss zone law or zone equation (Section 6.5.3) also applies to reciprocal lattice

planes: for the reciprocal lattice points (hkl) lying in the plane through the origin and

perpendicular to the lattice vector r

uvw

hu +kv + lw = 0

and for the reciprocal lattice points lying in the nth reciprocal lattice plane from the

origin:

hu +kv + lw = n.

You can easily ‘check’ these equations with reference to Fig. 6.11(b). For example,

reciprocal lattice point (130) lies in the ﬁfth plane in zone [210] and n = 1.2+3.1+0.0 =

5. For crystals with orthogonal axes and primitive unit cells, the spacings d

hkl

(of lattice

planes) and the spacings r

∗

uvw

(of reciprocal lattice planes) may be readily calculated (see

Section 6.5.4):

hkl



∗

hkl





(

∗

)

(

∗

)

(

∗

)





















∗

uvw



(

)

(

)

(

)



(

)

(

)

(

)

For crystals with centred lattices, analogous conditions apply to the symbols (uvw)

∗

for

reciprocal lattice planes as they do to (hkl) for lattice planes. For example, for the cubic

F lattice, for which the reciprocal lattice is cubic I (Section 6.4), u +v +w = an even

integer.

Now, having completed this chapter, you should feel as conﬁdentand familiar with the

concept of reciprocal space as you do with direct space—for as we shall see in subsequent

chapters, diffraction patterns reveal, or are imperfect images of, the reciprocal lattices

of crystals.

6.7 Summary

In thischapterwe have developed thereciprocallattice as a purelygeometricalexercise—

as simply a method of representing the orientations and spacings of planes in a crystal