Hammond C. The Basics of Crystallography and Diffraction

Подождите немного. Документ загружается.

184 The diffraction of light

The diffraction-limited resolution of a microscope can be treated in two ways. First,

it may be treated in the same way as for a telescope or camera—by considering the

separation between theAiry discs of two closely spaced points of light and situated close

to the front focal plane of the objective rather than (as in the telescope or camera) a

long distance away. In so doing a simplifying assumption is made that the light from

the two point sources is incoherent (just as in the case of two stars) and hence inter-

ference between them can be neglected (see Section 7.3). The assumption is generally

invalid—microscopial specimens do not consist of independent points of light of differ-

ent intensities across their surfaces. It is more reasonable to assume that the specimen

is illuminated with coherent light and that interference occurs between the light waves

diffracted at the light/dark regions across the specimen surface.

This leads us to the

second way of treating the diffraction-limited resolution of the microscope which was

ﬁrst developed by Ernst Abbe,

∗

the optical designer for Carl Zeiss.

It turns out from a rigorous analysis that the expressions for the limit of resolution

are closely identical irrespective of the assumptions made about the illumination or self-

illumination of the specimen. We shall follow both approaches, not least because they

serve as useful applications of the diffraction theory we have already learned.

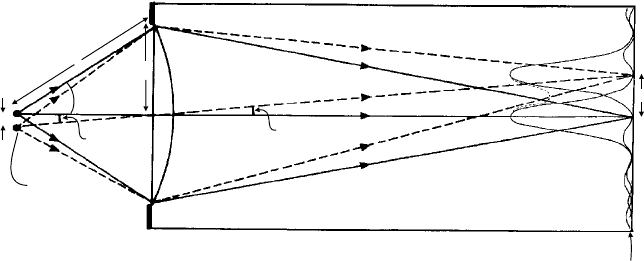
The ﬁrst approach is represented in Fig. 7.12 which shows two such points of light and

their Airy disc images—an axial point (solid lines) and an off-axis point (dashed lines).

In a microscope the plane in which the Airy disc images occur is called the primary

image plane—the plane which is ‘observed’ in the eyepiece.

Two point sources

separation

Primary

image

plane

zom

Fig. 7.12. The limit of resolution in a microscope for two points of light separated by distance a and

which subtend angle α

zom

at the objective lens. At this angle the zero order minimum of the Airy disc

of one point source corresponds with the central maximum of the Airy disc of the adjacent point source.

The sources are situated at a distance from the objective lens close to f , the focal length.

The condition for incoherent illumination is closely approached in the case of ﬂuorescence microscopy.

Otherwise, in the usual Köhler illumination arrangement (in which each point in the light source gives rise to

a parallel pencil of rays at the specimen as in Fig 7.6), the illumination is coherent.

∗

Denotes biographical notes available in Appendix 3.

7.5 The resolving power of optical instruments 185

Just as in a telescope, the limit of resolution is given when the angular separation

between the two point sources, α

zom

= 1.22λ/d (see Fig. 7.11). We now have to express

this limit in terms of a, the separation of the two point sources and i, the semi-angle

subtended by the objective lens at the point-sources. Let f be the focal length of the

objective lens as indicated in Fig. 7.12, then sin i = d /2f and α

zom

≈ a/f . Hence

zom

= 1.22λ/d = a /f from which a = 1.22λ/(f /d). Substituting (f /d) = 1/2 sin i

we obtain

limit of resolution = a =

1.22λ

2 sin i

0.61λ

sin i

In the case of microscope objectives of very small focal length (i.e. ‘high power’ objec-

tives), the space between the specimen and front element of the lens may be ﬁlled with a

drop of oil, of refractive index n, which is simply the ratio of the wavelength λ of light in

air (or vacuum) to the wavelength λ



in the oil, i.e. by deﬁnition n = λ/λ



. Substituting

this factor gives:

limit of resolution = a =

0.61λ



sin i

0.61λ

n sin i

The second approach, due to Ernst Abbe, is as follows: in order for the microscope

to form an image of the specimen (i.e. in order to resolve the slits or lines of a grating),

at least two beams (usually the direct beam and the ﬁrst order diffracted beam) should

enter the objective lens. This situation is shown in Fig. 7.13. The specimen/grating is

illuminated with a parallel beam of light (from a distant source or a sub-stage condenser

in which the aperture diaphragm is almost fully closed) and the ﬁrst order diffracted

beams (on either side of the direct beam) are just collected by the objective lens.

These parallel beams are then focused by the objective lens to give diffraction spots

which are situated, as shown, in its back focal plane (a screen placed here would record

Diffraction

grating

object

Incident

beam

Objective

lens

Back focal plane

of objective lens

(Primary) image

plane

Fig. 7.13. Image formation in the light microscope. The direct and diffracted beams enter the objective

lens and are focused to form a diffraction pattern in its (back) focal plane (compare with Fig. 7.6). The

rays ‘continue on their way’ to form an image by the recombination of the diffracted light, e.g. incident

ray X is separated into z (direct) and y (diffracted) light; these two rays recombine in the image plane.

186 The diffraction of light

this diffraction pattern, just as shown in Fig. 7.6). However, the beams or rays continue

on their way and intersect, as shown, to form the (primary) image, (which is then

magniﬁed by the eyepiece or photographic projection lens). The important point is that

the image is formed by the recombination of light which was separated at the specimen

by diffraction. Consider, for example, the incident beam marked X (Fig. 7.13); this is

separated by diffraction into z (direct beam) and y (diffracted beam). These two beams

then contribute to the separate (zero and ﬁrst order) diffractionspots, but then continue on

their way to be reunited or recombined and, as Abbe pointed out, it is this recombination

that constitutes an image. The greater the number of diffracted beams which are collected

by the objective lens and thence recombined, the closer the image approximates to the

object, but the limit of resolution is determined by the criterion that at least two beams

should enter the objective.

Hence, for the case of normal incidence, in which the direct and two ﬁrst order beams

enter the objective lens (Fig. 7.14(a)), the limit of resolution is simply obtained from the

(a)

(b)

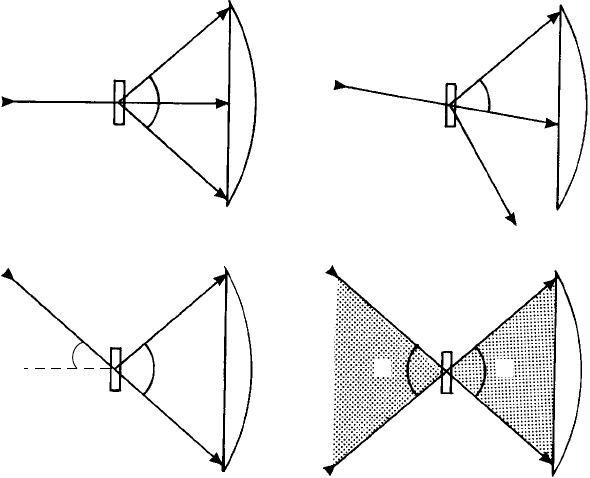
Fig. 7.14. TheAbbe criterion for the limit of resolution of an objective lens of (semi-angular) aperture

i. (a) normal incidence, parallel light (condenser diaphragm closed down); the direct and two ﬁrst-order

beams at angle i enter the objective and contribute to the image; (b) as (a) but a slightly inclined incident

parallel beam, the direct beam and just one ﬁrst-order beam enter the objective lens but at an angle

greater than i; (c) as (b) but the incident beam is inclined at the maximum angle i; it passes inside one

edge of the objective lens and one diffracted beam at angle 2i passes inside the opposite edge; (d) the

practical arrangement; the condenser diaphragm is opened to admit a convergent cone of light on to

the specimen (in practice rather less than 2i) to admit direct and diffracted light to the objective over a

whole range of angles.

7.5 The resolving power of optical instruments 187

equation derived in Section 7.4, i.e. 1λ = a sin α

= a sin i, i.e. the limit of resolution

a = λ/ sin i, where i is the semi-angle of the objective lens subtended at the specimen

which is set equal to α

the angle between the direct and ﬁrst order diffracted beams.

This equation may be modiﬁed in two ways. First, Fig. 7.13 shows an overfulﬁlled

case in which, because the incident beam is normal to the specimen and axial with the

microscope, two ﬁrst-order diffracted beams, as well as the direct or zero order beam,

enter the objective. This situation is sketched for emphasis in Fig. 7.14(a). However,

if the incident beam is inclined to the axis of the microscope as shown in Fig. 7.14(b),

then the ﬁrst order beam on one side of the direct beam is lost but a ﬁrst order beam on

the other side of the direct beam of greater diffraction angle can enter the objective lens.

The extreme or limiting case arises when the incident beam is inclined at angle i to the

microscope axis (Fig. 7.14(c)), in which case the direct or zero order beam just passes

inside one edge of the objective lens and one ﬁrst order diffracted beam, now at twice

the angle, 2i to the direct beam, just passes inside the opposite edge. The Abbe criterion

is still satisﬁed because two beams (zero order and ﬁrst order) enter the objective lens

and are recombined to form an image in the same way as shown in Fig. 7.13.

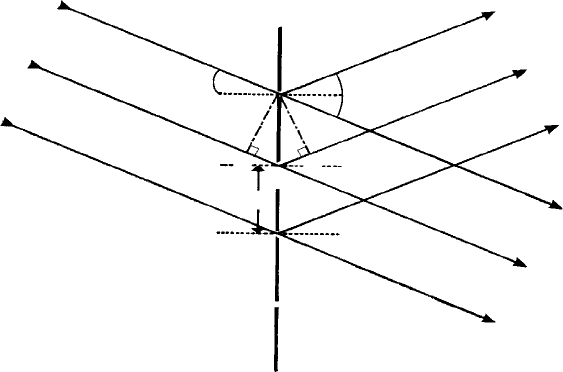
We must now work out the path difference for this inclined case. The geometry is

shown in detail in Fig. 7.15, which should be compared with that for normal incident light

shown in Fig. 7.5. The path difference between the direct and ﬁrst order diffracted beam

is now AB +BC = 1λ for constructive interference, i.e. a sin i +a sin i = 2a sin i. This

equation, it should be noted, is identical to the Bragg equation (see Section 8.3) since

both describe the same geometrical conditions: in both cases the incident and diffracted

Incident

beam

First order

diffracted

beam

Direct or

zero order

beam

Fig. 7.15. The geometry for constructive interference when the incident and diffracted beams make

equal angle i to the diffraction grating. For constructive interference (ﬁrst order) the path difference =

AB+BC=a sin i + a sin i = 2a sin i = 1λ. This condition is equivalent to Bragg’s law where a is the

interplanar spacing d and i is θ , the Bragg angle.

188 The diffraction of light

beams are at the same angle to the diffraction grating or lattice planes (i.e. i = θ) and

the grating spacing a corresponds to the interplanar spacing d.

Rearranging the equation gives:

limit of resolution = a =

2 sin i

0.5λ

sin i

which differs from our previous equation by a factor of 0.5.

Second, the space between the specimen and the front element of the objective lens

may be ﬁlled with oil of refractive index n. Proceeding as before:

limit of resolution = a =

0.5λ



sin i

0.5λ

n sin i

In practice we do not in general illuminate the specimen with a single parallel inclined

beam as shown in Fig. 7.14(c), but we open the aperture diaphragm of the condenser

lens to give a highly convergent beam on the specimen of semi-angle i (in practice

slightly less) as shown in Fig. 7.14(d). This is analogous, in terms of illumination, to

the case of the point sources of light radiating out in all directions as described above

and the equations for the limit of resolution which we have derived—one for incoherent

illumination (diffraction at the objective aperture) and the other for coherent illumination

(diffraction at the specimen)—are, except for theAiry factor 1.22, precisely the same.As

mentioned above, amuchmore rigorous analysis also predicts closely identical solutions.

The important quantity in the equations n sin i was called by Abbe the numerical

aperture, NA and fulﬁls, in effect, the same role with respect to the microscope as

does the aperture d of the objective lens (or mirror) with respect to the telescope. To

summarize:

Angular–limit of resolution of a telescope = α

zom

1.22λ

Distance–limit of resolution of a microscope = a =

0.61λ

0.5λ

The concept of numerical aperture NA = n sin i is of enormous importance in optics.

It is closely related to the f -number, the ratio of focal length/aperture, (f /d) of a lens.

Referring again to Fig. 7.12, since sin i = d/2f then (f /d ) = 1/2 sin i since sin i =

NA/n,

f -number, (f /d) =

NA.

The Abbe criterion applies equally to light microscopes and electron microscopes.

The enormous decrease in the limit of resolution obtainable in the transmission electron

microscope arises because of the much smaller values of λ for electrons (typically 4 pm

for 100 kV instruments compared with light (typically 500 nm)). This (approximate)

100 000 decrease is however offset because of the high inherent spherical aberrations in

electron lenses which limit NA values to the order of 0.01 compared with NA values up

to 1.4 for oil immersion light objectives.

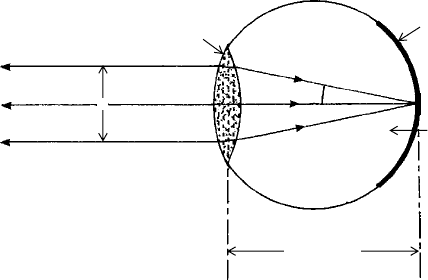
7.5 The resolving power of optical instruments 189

Lens

Retina

Vitreous

humour

n = 1.3

f ≈ 17 mm

Fig. 7.16. The components of the eye (a) considered as a telescope or camera (light path to the right),

the retina being the image plane. The angular-limit of resolution (for d = 3mm) = 0.77 min of arc

or 0.07 mm at the near distance of 250 mm. (b) The eye considered as a water-immersion microscope

objective (light path to the left), the retina being the object plane. The numerical aperture NA = 0.115

and the distance-limit of resolution = 2.9 μm (see text for calculations). These values correspond (a)

for visual acuity of ≈0.1 mm at 250 mm and (b) to the spacing of the central retinal cone cells.

Finally, we may apply these ideas to those most important and precious optical

instruments—our eyes.

We may treat the eye either as a telescope or camera to determine the angular-limit of

resolution between two distant points, or as a microscope, with the direction of the light

in effect reversed, to determine the distance-limit of resolution at the retina, the space

between the objective (eye) lens and the retina (corresponding to the microscope object

or specimen-plane) being ﬁlled with liquid (the vitreous humour) of refractive index n

(see Fig. 7.16).

If we take f = 17 mm, n = 1.3, d (the diameter of the pupil) ≈3 mm (which varies

of course roughly in the range 1 ∼ 4 mm depending on the intensity of the light) and λ

(for green light) ≈0.55 μm, then the f -number of the eye is (17/3) mm = 5.67 and the

numerical aperture NA is 1.3/2(5.67) = 0.115.

Substituting these values of λ and d into the expression for the angular-limit of

resolution α

zom

gives 0.22 × 10

−3

rads or 0.77 min of arc which is close to that for

normal vision (∼1 min of arc or 0.07 mm at the near distance of 250 mm).

Similarly, substitution of these values of λ and d into the expression for the distance-

limit of resolution a at the retina gives 2.9 μm—which is approximately equal to the

spacing of our visual receptors (the cone cells) in the central part (the fovea centralis)of

our retina. In short, our eyes have evolved, as we should expect, with a perfect balance

between the sizes of their physiological components.

A note on light and radio telescopes

It is of interest to compare the performance of light and radio telescopes with regard to

the observation of extragalactic objects. The equation for the angular-limit of resolution,

190 The diffraction of light

zom

1.22λ

, applies (approximately) equally to radio telescopes where d is now

the diameter of the paraboidal receiving dish and λ is in the range 5 cm upwards. For

λ = 1 m and d = 100 m we obtain α

zom

= 0.012 rads = 42 min of arc—a resolution

inferior to that of the human eye. However, it should be noted that substantially decreased

limits of resolution are obtained by interferometric techniques, i.e. by linking the signals

from widely spaced radio telescopes. Resolutions down to a thousandth of an arc second

or so are obtainable using the technique of very long baseline interferometry (VLBI).

This is superior to anything that can be presently obtained using optical telescopes.

Radio telescopes also have the advantage of using larger area collecting dishes than is

currently possible with optical telescopes. They therefore enable very faint radio sources

to be detected.

Exercises

7.1 Figure 7.17(a)shows anet with asingle twinand thecorresponding diffraction pattern (optical

transform) and Fig. 7.17(b) shows a net with several twins and the corresponding diffraction

(a)

(b)

Fig. 7.17. (a) A net with a single twin, and (b) a net with several twins and their corresponding

diffraction patterns (from Atlas of Optical Transforms by G. Harburn, C. A. Taylor and T. R. Welberry,

Bell & Hyman, 1983, an imprint of HarperCollins).

Exercises 191

pattern (see Figs. 1.18, 1.21 and 4.4(b)). Using a tracing paper overlay on the diffraction

pattern in Fig. 7.17(a), outline the reciprocal lattice unit cells of the two twin orientations

and note those reciprocal lattice points which are common to both twin orientations.

The diffraction pattern in Fig. 7.17(b) is similar to that in Fig. 7.17(a) except that some of

the spots are streaked in a direction perpendicular to the twin plane. Explain this streaking

qualitatively after you have read Section 9.3.

7.2 With reference to Fig. 7.7(c), describe the diffraction pattern which you would obtain with

a diffraction grating in which the slit width d is equal to half the slit spacing a.

X-ray diffraction: the

contributions of Max von Laue,

W. H. and W. L. Bragg and

P.P. Ewald

8.1 Introduction

The experimental technique which has been of the greatest importance in revealing the

structure of crystals is undoubtedly X-ray diffraction.

The story of the discovery of X-ray diffraction in crystals by Laue,

∗

Friedrich and

Knipping in Munich in 1912 and the development of the technique by W. H. Bragg

∗

and W. L. Bragg

∗

in Leeds and Cambridge in the years preceding the First World War is

well known. But why did the Braggs make such rapid advances in the analysis of X-ray

diffraction photographs in comparison with Laue and his co-workers? An important fac-

tor in the answer seems to be that Laue envisaged crystals in terms of a three-dimensional

network of rows of atoms and based his analysis on the notion that the crystal behaved,

in effect, as a three-dimensional diffraction grating. This approach is not wrong, but it

is in practice rather clumsy or protracted. On the other hand, the Braggs (and here the

credit must go to W. L. Bragg, the son) envisaged crystals in terms of layers or planes

of atoms which behaved in effect as reﬂecting planes (for which the angle of incidence

equals the angle of reﬂection), strong ‘reﬂected’ beams being produced when the path

differences between reﬂections from successive planes in a family is equal to whole

number of wavelengths. This approach is not correct in a physical sense—planes of

atoms do not reﬂect X-rays as such—but it is correct in a geometrical sense and provides

us with the beautifully simple expression for the analysis of crystal structure:

nλ = 2d

hkl

sin θ,

where λ is the wavelength, n is the order of reﬂection, d

hkl

is the lattice plane spacing

and θ is the angle of incidence/reﬂection to the planes.

What led W. L. Bragg to this novel perception of the diffraction? Simply his obser-

vation of the elliptical shapes of the diffraction spots, which he noticed were also

characteristic of the reﬂections from mirrors of a pencil-beam of light (see the Laue

photograph on p. xiv). Only connect!

∗

Denotes biographical notes available in Appendix 3.

8.2 Laue’s analysis of X-ray diffraction: the three Laue equations 193

Finally, we come to the contribution of P. P. Ewald,

∗

a physicist who never achieved

the recognition that was his due. The story is brieﬂy recorded in his autobiographical

sketch in 50 Years of X-ray Diffraction. Ewald was a ‘doctorand’—a research student

working in the Institute of Theoretical Physics in the University of Munich under Pro-

fessor A. Sommerfeld. The subject of his thesis was ‘To ﬁnd the optical properties of

an anisotropic arrangement of isotropic oscillators’. In January 1912, while he was in

the ﬁnal stages of writing up his thesis, he visited Max von Laue, a staff member of

the Institute, to discuss some of the conclusions of his work. Ewald records that Laue

listened to him in a slightly distracted way and insisted ﬁrst on knowing what was

the distance between the oscillators in Ewald’s model; perhaps 1/500 or 1/1000 of the

wavelength of light, Ewald suggested. Then Laue asked ‘what would happen if you

assumed very much shorter waves to travel through the crystal?’ Ewald turned to Para-

graph 6, Formula 7, of his thesis manuscript, saying ‘this formula shows the results of

the superposition of all wavelets issuing from the resonators. It has been derived with-

out any neglection or approximation and is therefore valid also for short wave-lengths.’

Ewald copied the formula down for Laue shortly before taking his leave, saying that

he, Laue, was welcome to discuss it. Laue’s question, of course, arose from his intu-

itive insight that if X-rays were waves and not particles, with wavelengths very much

smaller than light, then they might be diffracted by such an array of regularly spaced

oscillators.

The next Ewald heard of Laue’s interest was through a report which Sommerfeld gave

in June 1912 on the successful Laue–Friedrich–Knipping experiments. He realized that

the formula which he had copied down for Laue, and which Laue had made no use of,

provided the obvious way of interpreting the geometry of the diffraction patterns—by

means of a construction which he called the reciprocal lattice and a sphere determined

by the mode of incidence of the X-rays on the crystal (the Ewald or reﬂecting sphere).

Ewald’s interpretation of the geometry of X-ray diffraction was not published until 1913,

by which time rapid progress in crystal structure analysis had already been made by W. H.

and W. L. Bragg in Leeds and Cambridge.

8.2 Laue’s analysis of X-ray diffraction:

the three Laue equations

Laue’s analysis of the geometry of X-ray diffraction patterns has been referred to in

Section 8.1. What follows is a much simpliﬁed treatment which does not take into

consideration Laue’s interpretation of the origin of the diffracted waves from irradiated

crystals.

Consider a simple crystal in which the motif is one atom and the atoms are simply

to be regarded as scattering centres situated at lattice points. The more general situation

in which the motif consists of more than one atom and in which the different scattering

amplitudes of the atoms and the path differences between the atoms have to be taken into

account is discussed in Section 9.2. The crystal may be considered to be built up of rows

∗

Denotes biographical notes available in Appendix 3.