Hammond C. The Basics of Crystallography and Diffraction

Подождите немного. Документ загружается.

124 Crystal symmetry

(a) (b) (c)

(d)

(f) (g) (h)

(i) (j)

(e)

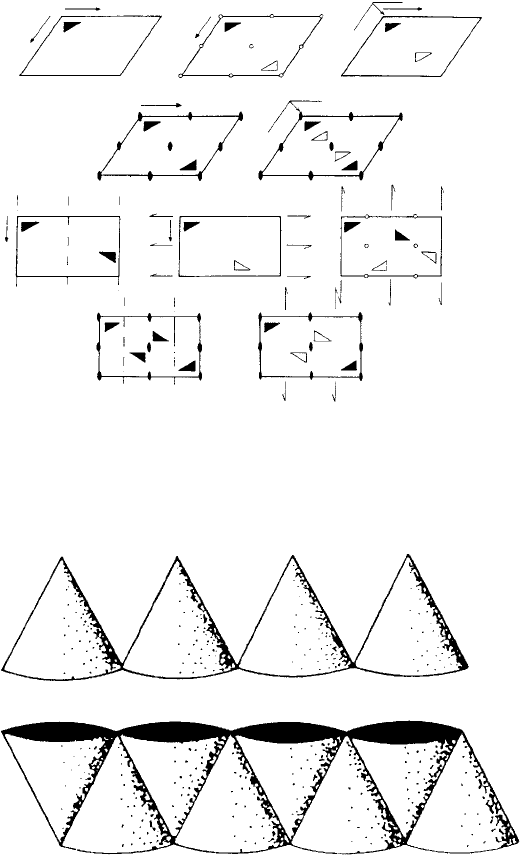
Fig. 4.18. Representation of the ten symmetry groups allowing coordination close packing of three-

dimensional motifs in a plane. Single-headed arrows indicate in-plane screw diads, dashed lines indicate

vertical mirror planes (from Macromolecular Physics, Volume 1, by B. Wunderlich, Academic Press,

New York and London, 1973).

(a)

(b)

Fig. 4.19. Representation using a cone as a motif of the packing of (a) polar and (b) non-polar layers

(from Macromolecular Physics, Volume 1, by B. Wunderlich, Academic Press, New York and London,

1973).

4.8.2 L ong-chain polymer molecules

The crystal structures and space groups formed by long-chain polymer molecules are

also in accord with the principles outlined above.

4.8 The crystal structures and space groups of organic compounds 125

In the case of atactic polymers (i.e. those in which the side-groups are large and/or

randomly distributed along the chain), crystal structures rarely occur—the side-groups

keep the chains well apart—hence the name atactic. Crystal structures only occur in

tactic polymers in which the side-groups are regularly distributed on one side of the

chain (isotactic) or alternatively each side (syndiotactic). We shall consider just two

polymers—polyethylene (polythene) and isotactic polypropylene (polypropene).

Polyethylene n(CH

) is the simplest polymer, made up of a planar zig-zag chain of

carbon atoms, each carbon tetrahedrally coordinated to two hydrogen atoms. Two crystal

structures occur, polyethylene I (orthorhombic, space group Pnam—equivalent to Pnma

by change of axes) and polyethylene II (monoclinic, space group C



). Polyethylene I

is the common, stable form and the arrangement of the chains in the unit cell is shown in

Fig. 4.20(a). The zig-zag planes of the chains are at 45

◦

to the unit cell axes and are so

arranged that the protrusions of one chain ﬁt into the ‘hollow’ or recess formed by three

neighbouring chains as is also shown in Fig. 4.20(a) by the outlines or the envelopes of

the molecules. Screw diad axes of symmetry run in the directions of all three axes in the

unit cell—principally along and through the centres of the chains.

Table 4.1 Space groups for closest, limitingly and permissible close packing.

Motif symmetry Closest packed Limitingly close packed Permissible

1, P2

,P2

/c,Pca2

Pna2

,P2

None P1, C

, C2, P2

Pbca

1, P2

/c,C2/c,Pbca None Pccn

2 None C2/c,P2

2, Pbcn C2, Aba2

m None Pmc2

,Cmc2

,Pnma C

,P2

/m,Pmn2

Abm2, Ima2, Pbcm

(a)

Fig. 4.20. (continued)

126 Crystal symmetry

3Å

B

A

(b)

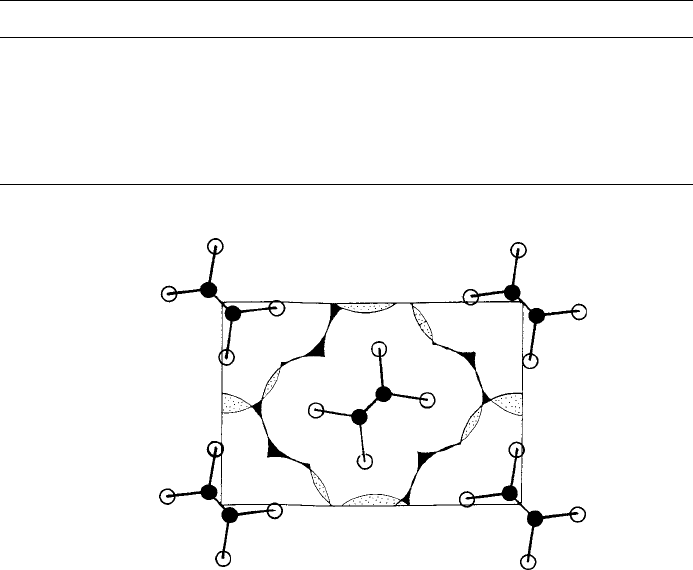
Fig. 4.20. Projections of polymer unit cells perpendicular to the chain axes. (a) Polyethylene, space

group Pnam, the centres of the carbon and hydrogen atoms in the planar zig-zag chains are shown by

black and open circles respectively; the envelopes of the molecules show clearly the close packing (from

Macromolecular Physics, Volume 1, by B. Wunderlich, Academic Press, New York and London, 1973).

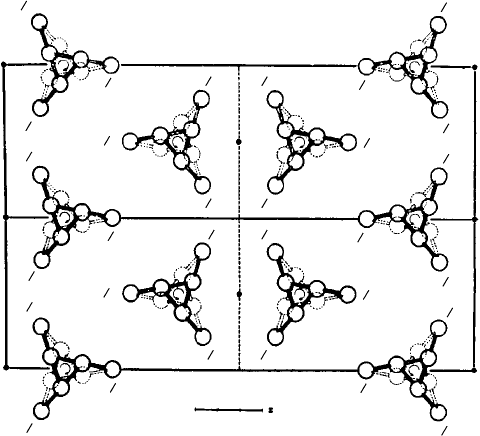
(b) Isotactic polypropylene, space group P 2

/c; the senses of the helices are indicated by the  and 

symbols (from Structure and properties of isotactic polypropylene by G. Natta and P. Corradini, Nuovo

Cimento, Suppl. to Vol 15 1, 40, 1960).

In polypropylene (polypropene), n(CH

-CHCH

), the CH

side-groups approach

too closely for the backbone to remain planar and their efﬁcient packing results in

the backbone being twisted into a helical conformation, both right and left handed.

In isotactic polypropylene the crystal structure is monoclinic and the space group is



—the commonest space group of all. Figure 4.20(b) shows a projection of the

unit cell perpendicular to the chain axes. The packing together of the helices is dictated

by the intermeshing of the CH

side-groups and this occurs most efﬁciently when the

rows of helices along the c-axis are alternatively right and left handed as shown in Fig.

4.20(b). The packing is, in fact, very close to hexagonal, like a bundle of pencils, and

an hexagonal unit cell may also occur. (Figure 10.11(b) shows a ﬁbre photograph of

isotactic polypropylene and Exercise 10.4 shows how the orientation of the chains in the

unit cell may be determined.)

4.9 Quasiperiodic crystals or crystalloids

The 230 space groups represent all the possible combinations of symmetry elements,

and therefore all the possible patterns which may be built up by the repetition, without

4.9 Quasiperiodic crystals or crystalloids 127

any limit, of the structural units of atoms and molecules which constitute crystals. But

real crystals are ﬁnite and the atoms or molecules at their surfaces obviously do not

have the same environment as those inside. Moreover, crystals nucleate and grow not

according to geometrical rules as such but according to the local requirements of atomic

and molecular packing, chemical bonding and so on. The resulting repeating pattern or

space group is the usual consequence of such requirements, but it is not a necessary

one. We will now consider some such cases where ‘crystals’ nucleate and grow such

that the resulting pattern of atoms or molecules is non periodic and does not conform to

any of the 230 space groups—in short the three-dimensional analogy to the non-periodic

patterns and tilings discussed in Section 2.9. But ﬁrst we need to adopt a new name

for such structures and, following Shechtman

can call them quasiperiodic crystals or

materials, or following Mackay

call them crystalloids.

We will start ‘where we began’ in Section 1.1 of this book by model-building with

equal size closely packed spheres. In the ccp structure, as we have seen, each sphere is

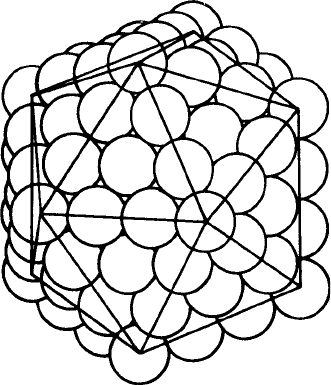
surrounded or coordinated by 12 others as shown in Fig. 4.21(a). The polyhedron formed

around the central sphere is a cubeoctahedron. It is one of the thirteen semi-regular

or Archimedean solids (see Sections 3.4 and Appendix 2). However, even though all the

spheres are close-packed, they are not all evenly distributed around the central sphere

the interstices between them are different: some ‘square’, some ‘triangular’.

(a) (b) (c)

Fig. 4.21. (a) The close packing of 12 spheres around a central sphere as in the ccp structure. The solid

is a cubeoctahedron; note that the spheres are not evenly distributed round the central sphere, some of

the interstices are square, some triangular, (b) The twelve spheres shifted to obtain an even distribution;

note that the spheres are surrounded by, but not in contact with, ﬁve others. (c) The spheres brought

together such that they are now in contact; the central sphere is now ∼10% smaller. The solid now has

the 20 triangular faces of an icosahedron (see also note on pp. 129–30).

D. Shechtman, I. Blech, D. Gratias and J. W. Cahn. ‘Metallic phase with long-range orientational order

and no translational symmetry.’ Phys. Rev. Lett. 53, 1951 (1984).

A. L. Mackay. Phys. Bull. p. 495 (1976).

128 Crystal symmetry

Now, we can shift the spheres around the central sphere to obtain an even distribution

and as we see (Fig. 4.21(b)), this occurs when each sphere is surrounded by (but not

now touching) ﬁve others and with ‘open’ triangular interstices between them. (This

operation is best carried out by making the central sphere out of soft modelling clay and

using pegs sticking from the spheres into the clay to keep them in place.) Finally, we can

squeeze the whole model (i.e. compress the central sphere) in our cupped hands to bring

all the spheres into contact and make a close-packed shell of 12 spheres as shown in Fig.

4.21(c). We have created icosahedral packing because the solid has the 20 triangular

faces of an icosahedron. The central sphere or interstice now has a radius some 10%

smaller than the 12 surrounding spheres.

The icosahedron can be extended by adding a second, then a third shell of spheres, the

spheres succeeding each other to give cubic close packing on each of the 20 triangular

faces (Fig. 4.22). Icosahedral packing is not the densest packing (cubeoctahedral pack-

ing is the densest), nor is it crystallographic packing—the non-repeating pattern of the

shells of spheres constitutes a crystalloid with point group symmetry 2

5 indicating the

presence of 30 two-fold, 20 three-fold and 12 ﬁve-fold axes of symmetry. It is, however,

an extremely stable structure (the spheres naturally ‘lock’together during the squeezing

operation) and it is the basis of Buckminster Fuller’s construction of geodesic domes

(Section 1.11.6) as well as being characteristic of many virus structures (e.g. the polio

virus) which makes them so indestructible.

Icosahedral structuresalsooccur in several metallicalloys, in particularthose based on

aluminium with copper, iron, ruthenium, manganese, etc. These quasiperiodic crystals

were ﬁrst recognised (in an Al-25% Mn alloy) from the ten-fold symmetry of their

electron diffraction patterns (i.e. ﬁve-fold symmetry) plus a centre of symmetry resulting

from diffraction—Friedel’s law—see Section 9.2). Many such quasiperiodic crystals,

Fig. 4.22. Icosahedral packing of spheres showing close-packing on each of the 20 triangular faces

(from ‘A dense non-crystallographic packing of equal spheres’, by A. L. Mackay, Acta. Cryst. 15, 916,

1962).

4.9 Quasiperiodic crystals or crystalloids 129

Fig. 4.23. A quasicrystal of a 63% Al, 25% Cu-11% Fe alloy showing pentagonal dodecahedral

faces (from ‘A stable quasicrystal in Al-Cu-Fe system’ by An-Pang Tsai, Akihisa Inoue and Tsuyoshi

Masumoto, Jap. J. Appl. Phys. 26, 1505, 1987).

formed by rapid solidiﬁcation from the melt, are metastable and revert to crystalline

structures on heating, but stable quasiperiodic crystals as large as a few millimetres

in size have been prepared. Figure 4.23 is a scanning electron micrograph of a 63%

Al-25% Cu-11% Fe alloy quasicrystal showing the existence of beautiful pentagonal

dodecahedral faces. The pentagonal arrangement of atoms in such a face can be revealed

by scanning tunnelling microscopy of carefully prepared surfaces and Fig. 4.24 shows

such a (Fourier ﬁltered) image of the quasicrystalline alloy Al

. Icosahedral

shells of atoms may also occur as the motif within crystal structures. For example, the

alloy MoAl

consists of Mo atoms surrounded by icosahedral shells of 12 Al atoms,

the icosahedra themselves being packed together in a bcc array.

Icosahedral groups of molecules also occur in a number of gas hydrates which can be

crystallized in the form of highly hydrated solids, called clathrates. For example, chlorine

hydrate, Cl

O, hasa body-centred cubic structureat the centreandcorners of whichthe

water molecules are arranged at the corners of pentagonal dodecahedra—an arrangement

analogous to dodecahedrene (see Section 1.11.6). Further water molecules occupy the

interstices between four such dodecahedra and the chlorine molecules are ‘imprisoned’

within this framework—hence the name clathrate, meaning latticed or screened.

A note on the transformation from crystallographic to quasiperiodic

atom packing

The transformation from the cubeoctahedron to the icosahedron (Fig 4.21 and the front

cover illustration of this book) may be described in another way. In cubic close-packing

130 Crystal symmetry

Fig. 4.24. Image (10 nm ×10 nm) of a surface of the alloy Al

showing the ﬁve-fold ‘dark

star’ quasiperiodic pattern. (Photograph by courtesy of Prof. Ronan McGrath, University of Liverpool.)

the ‘middle’ ring of six atoms is planar with a group of three close-packed atoms above

and three below. In icosahedral packing the corresponding ring of six atoms is puckered

(resulting in a ∼10% smaller central cavity) with again three close-packed atoms above

and three below. Hence, the transformation may proceed by such small displacive atom

movements.

Exercises

4.1 Draw the space group Pba2 with the pattern unit  at the following positions:

(a) on the b glide plane, i.e. at







;

(b) at the intersections of the a and b glide planes, i.e. at







;



);

(d) on a diad axis through the mid-points of the cell edges, i.e. at







Hence, show that only (c) and (d) constitute special positions.

4.2 Make and examine the crystal models of NaCl, CsCl, diamond, ZnS (sphalerite), ZnS

(wurtzite), Li

OorCaF

(ﬂuorite), CaTiO

(perovskite). Identify the Bravais lattice and

describe the motif of each structure.

Describing lattice planes and

directions in crystals: Miller

indices and zone axis symbols

5.1 Introduction

In previous chapters we have described the distributions of atoms in crystals, the sym-

metry of crystals, and the concept of Bravais lattices and unit cells. We now introduce

what are essentially shorthand notations for describing directions and planes in crystals

(whether or not they correspond to axes or planes of symmetry). The great advantages of

these notations are that they are short, unambiguous and easily understood. For example,

the direction (or zone axis) symbol for the ‘corner-to-corner’ (or triad axis) directions

in a cube is simply



111



. The plane index (or Miller index) for the faces of a cube is

simply {100} or of an octahedron {111} (Fig. 4.1). The various faces and the directions

of their intersections in crystals such as those illustrated in Fig. 4.3 can also be precisely

described using these notations. Without them one would have to resort to carefully

scaled drawings or projections.

Now direction symbols and plane indices are based upon the crystal axes or lattice

vectors which outline or deﬁne the unit cell (see Section 3.2) and the only ambiguities

which can arise occur in those cases in which different unit cells may be used. For

example, crystals with the cubic F Bravais lattice may be described in terms of the

‘conventional’face-centred cell (Fig. 1.6) or in terms of the primitive rhombohedral cell

(Fig. 1.7). Because the axes are different, the direction symbols and plane indices will

also be different. Hence it is important to know (1) which set of crystal axes, or which

unit cell, is being used and (2) how to change or transform direction symbols and plane

indices when the set of crystal axes or the unit cell is changed. This topic is covered in

Section 5.8. It is a serious problem only in the case of the trigonal system for crystals with

a rhombohedral lattice where there are two almost equally ‘popular’ unit cells—unlike,

say, the rhombohedral cells for the cubic Fand cubic I lattices which are rarely used. In

addition, in the trigonal and hexagonal systems it is possible to introduce, because of

symmetry considerations, a fourth axis, giving rise to ‘Miller-Bravais’plane indices and

‘Weber’ direction symbols, each of which consist of four, rather than three, numbers.

This topic is covered in Section 5.7, but ﬁrst the concept of a zone and zone axis needs

to be explained, a topic which is covered in more detail in Section 5.6.

A zone may be deﬁned as ‘a set of faces or planes in a crystal whose intersections

are all parallel’. The common direction of the intersections is called the zone axis.

All directions in crystals are zone axes, so the terms ‘direction’ and ‘zone axis’ are

132 Describing lattice planes and directions in crystals

synonymous. So much for the deﬁnition. The concept of a zone is readily understood by

examining an ordinary pencil. The six faces of a pencil all form or lie in a zone because

they all intersect along one direction—the pencil lead direction—which is the zone axis

for this set of faces. The number of faces in a zone is not restricted and the faces need not

be crystallographically equivalent. For example, the edges of a pencil may be shaved

ﬂat to give a 12-sided pencil, i.e. an additional six faces in the zone. Or consider an

orthorhombic crystal (Fig. 3.5(b)), or a matchbox. Each crystal axis is the zone axis for

four faces, or two crystallographically equivalent pairs of faces. Each face lies in two

zones; for example, the ‘top’ and ‘bottom’ faces of Fig. 3.5(b) lie in the zones which

have the x- and y-directions as zone axes. In general, a face or plane in a crystal belongs

to a whole ‘family’ of zones, the zone axes of which lie in or are parallel to the face.

Verbal deﬁnitions are frequently rather clumsy in relation to the simple concepts

which they seek to express. Take a piece of paper and draw on it some parallel lines.

Fold the paper along the lines—and there you have a zone!

5.2 Indexing lattice directions—zone axis symbols

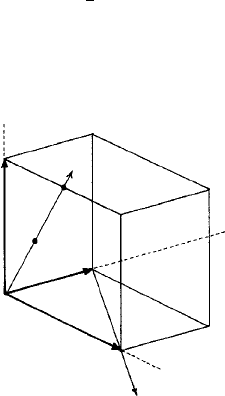
First, the direction whose symbol is to be determined must pass through the origin of the

unit cell. Consider the unit cell shown in Fig. 5.1, which has unit cell edge vectors a, b, c

(which are not necessarily orthogonal or equal in length)

. The steps for determining the

zone axis symbol for the direction OL are as follows. Write down the coordinates of a

point—any point—in this direction—say P—in terms of fractions of the lengths a, b and

c, respectively. The coordinates of P are

, 0, 1. Now express these fractions as the ratio

of whole numbers and insert them into [square] brackets without commas; hence [102].

This is then the direction or zone axis symbol for OL. Notice that if we had chosen a

Fig. 5.1. Primitive unit cell of a lattice deﬁned by unit cell vectors a, b, c. OL and SN are directions

[102] and [1

10] respectively.

See Appendix 5 for a simple introduction to vectors.

5.3 Indexing lattice planes—Miller indices 133

different point along OL—say Q—with coordinates

,0,

, we would have obtained

the same result.

Now consider the direction SN. To ﬁnd its direction symbol the origin must be shifted

from O to S. Proceeding as before (e.g. ﬁnding the coordinates of G with respect to the

origin at S) gives the direction symbol [1

10] (pronounced one bar-one oh), the bar or

minus sign referring to a coordinate in the negative sense along the crystal axis.

Directions in crystals are, of course, vectors, which may be expressed in terms of

components on the three unit cell edge or ‘base’vectors a, b and c. In the above example

the direction OL is written

102

= 1a +0b +2c .

The general symbol for a direction is [uvw] or, written as a vector,

uvw

= ua + vb + wc.

The direction symbols for the unit cell edge vectors a, b and c are [100], [010] and

[001], and very often these symbols are used in preference to the terms x-axis, y-axis

and z-axis.

5.3 Indexing lattice planes—Miller indices

First, for reasons which will be apparent shortly, the lattice plane whose index is to be

determined must not pass through the origin of the unit cell, or rather the origin must

be shifted to a corner of the cell which does not lie in the plane. Consider the unit cell

in Fig. 5.2 (identical to Fig. 5.1 but drawn separately to avoid confusion). We shall

determine the index of the lattice plane which is shaded and outlined by the letters RMS.

It is important ﬁrst to realize that this plane extends indeﬁnitely through the crystal; the

shaded area is simply that portion of the plane that lies within the unit cell of Fig. 5.2.

It is also important to realize that we are not just considering one plane but a whole

family of identical, parallel planes passing through the crystal. The next plane ‘up’ in

Fig. 5.2. Primitive unit cell (identical to Fig. 5.1), showing the ﬁrst two planes, RMS and PGFH, in

the family. These planes are shaded within the conﬁnes of the unit cell.