Хамханова Д.Н. Основы квалиметрии

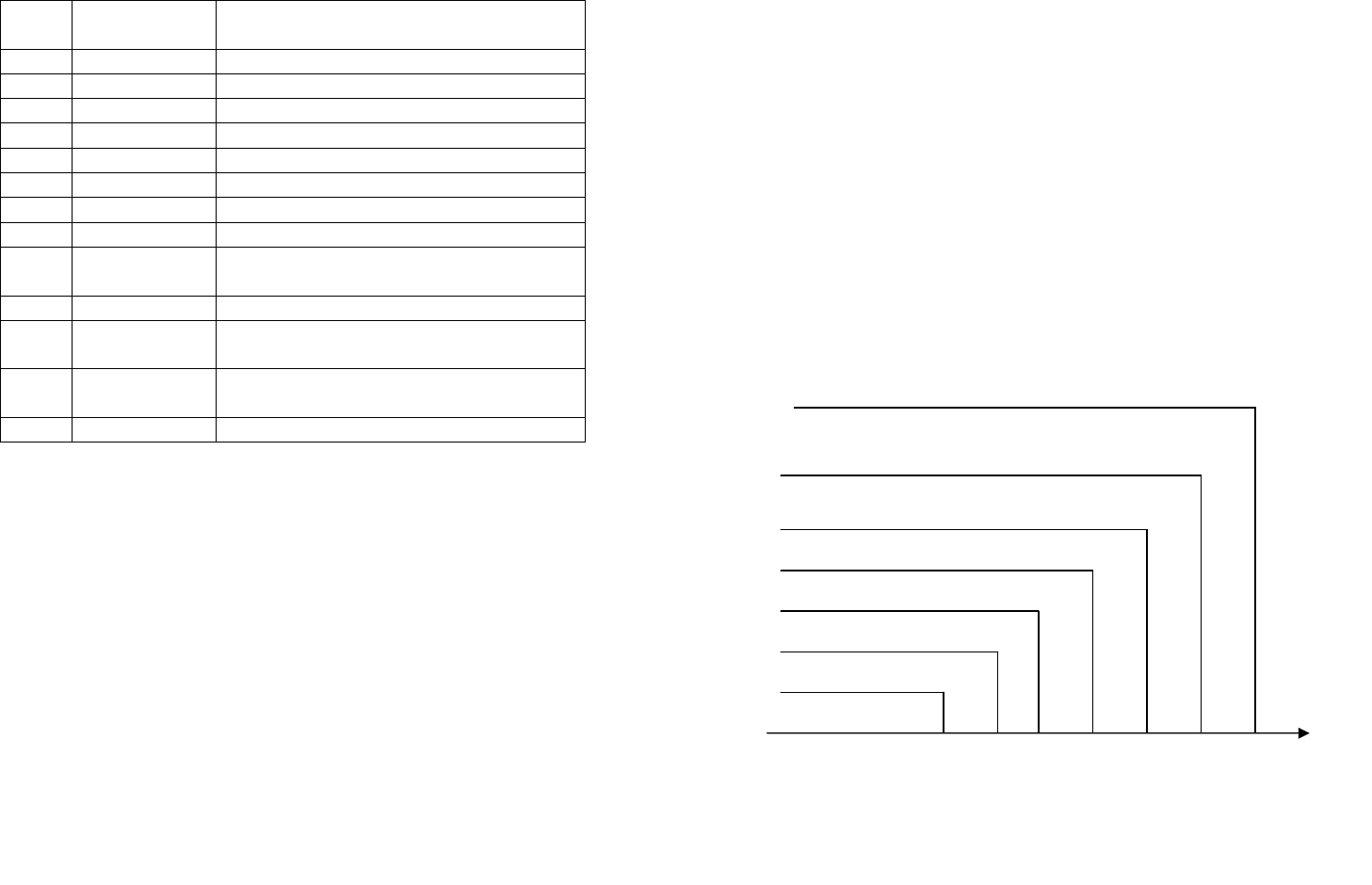
Таблица 4

Балл Название

ветра

Действие

0 Штиль Дым идет вертикально

1 Тихий Дым идет слегка наклонно

2 Легкий Ощущается лицом, шелестят листья.

3 Слабый Развеваются флаги

4 Умеренный Поднимается пыль

5 Свежий Вызывает волны на воде

6 Сильный Свистит в вантах, гудят провода

7 Крепкий На волнах образуется пена

8 Очень

крепкий

Трудно идти против ветра

9 Шторм Срывает черепицу

10 Сильный

шторм

Вырывает деревья с корнем

11 Жестокий

шторм

Большие разрушения.

12 Ураган Опустошительное действие

Шкала интервалов.

Более совершенными в этом отношении являются шкалы

интервалов, составленные из строго определенных

интервалов. На шкале интервалов откладывается разность

между размерами. Общепринятой является измерение

времени по шкале, разбитой на интервалы, равные периоду

обращения Земли вокруг Солнца (летоисчесление). Эти

интервалы (годы) делятся в свою очередь на более мелкие

(сутки), равные периоду обращения Земли вокруг оси. Сутки в

свою очередь делятся на часы, часы на минуты, минуты на

секунды. Такая шкала называется шкалой интервалов

Принцип построения шкалы интервалов для размеров,

образующих ранжированный ряд Q

1

,<Q

2

<

Q

3

< Q

4

<Q

5

<

Q

6

<

Q

7

, показан на рис.5.

Математической моделью теоретического сравнения

между собой двух размеров одной меры служит выражение

ijji

QQQ

Δ

=

−

(51)

в котором при построении шкалы интервалов с размером

j

Q

сравниваются все размеры

i

Q

.

На рис. 5 в качества

j

Q

выбран четвертый размер. Если

бы в качестве

j

Q

был бы выбран размер

5

Q

, произошло бы

смещение нуля вправо, а если

3

Q

, то влево.

Начало отсчета на шкале интервалов произвольное.

Q

7

Q

6

Q

5

Q

4

Q

3

Q

2

Q

1

Q

Δ

−

2

Q

Δ

−

3

Q

Δ

−

0

5

Q

Δ

6

Q

Δ

7

Q

Δ

Q

Рис. 5. Построение шкалы интервалов для семи

размеров

79 80

На шкале интервалов определены такие математические

действия, как сложение и вычитание. Интервалы с учетом

знаков можно складывать друг с другом и вычитать друг из

друга. Благодаря этому можно определить, на сколько один

размер больше или меньше другого.

5757

QQQQ Δ−

Δ

=

−

()

255525

QQQQQQ

Δ

+

Δ

=Δ−−

Δ

=

−

(52)

()

311313

QQQQQQ

Δ

−

Δ

=

Δ−−

Δ

−

=

−

.

Аддитивные операции по формуле (52) выполняются с

размерами интервалов, полученных по формуле (51), т.е. по

неотградуированной шкале. Если шкала отградуирована, то

размеры единиц выражены в определенных единицах

измерения. По отградуированной шкале остаются

справедливыми формулы (52).

Ввиду неопределенности начала отсчета

мультипликативные операции на шкале интервалов не

определены. Соответственно на шкале интервалов нельзя

определять во сколько раз один размер больше или меньше

другого. Например, при любом летоисчеслении коренной

перелом в ходе второй мировой войны произошел под

Сталинградом спустя 700 лет после разгрома Александром

Невским немецких рыцарей Ливонского ордена на льду

Чудского озера. Если поставить вопрос о том, «во сколь раз

позже наступило это событие, то окажется, что по нашему

григорианскому стилю в 1942/1241=1,56 раза, по юлианскому

календарю, отсчитывающему время от «сотворения мира», - в

7448/6748=1,10 раза, по иудейскому, где время отсчитывается

«от сотворения Адама», - в 5638/4938=1,14 раза, а по

магометскому летоисчеслению, начатому с даты бегства

Магомета из Мекки в священный город Медину, где была

обоснована первая мусульманская община, - 1320/620=2,13

раза.

Иногда шкалы интервалов иногда получают путем

пропорционального деления интервала между реперными

точками. Так, на температурной шкале Цельсия за начало

отсчета принята температура таяния льда. С ней сравниваются

все другие температуры. Для удобства пользования шкалой

интервалов шкала между температурой таяния льда и

температурой кипения воды разбит на 100 равных интервалов

– градации или градусов. Вся шкала Цельсия разбита на

градусы как в сторону положительных, так и в сторону

отрицательных интервалов (рис.6).

Рис. 6. Температурные шкалы Цельсия (

0

С), Реомюра (

0

R),

Фаренгейта (

0

F) и Кельвина (

0

К).

81 82

На температурной шкале Реомюра за начало отсчета

принята та же температура таяния льда, но интервал между

этой температурой и температурой кипения воды разбит на 80

равных частей. Тем самым используется другая градация

температуры: температура Реомюра больше чем температура

Цельсия.

На температурной шкале Фаренгейта тот же интервал

разбит на 180 частей. Следовательно, градус Фаренгейта

меньше градуса Цельсия. Кроме того, начало отсчета

интервалов на шкале Фаренгейта сдвинут на 32

0

в сторону

низких температур.

Деление шкалы на рваные части – градации –

устанавливает на ней масштаб и позволяет выразить результат

измерения в числовой мере. При наличии масштаба измерение

на шкале интервалов сводится к подсчету числа градации,

укладывающихся в интервале

ij

QΔ

Структурная схема средства измерений по шкале

интервалов представлена на рис.7.

i

Q

[]

Q

Рис. 7. Структурная схема средства измерения по шкале

интервалов

В устройстве сравнения осуществляется операция. Так

как размер

j

Q

, с которым производится сравнение, остается

одним и тем же при разных

i

Q

,

подавать его всякий раз на

вход средства измерений нет необходимости. Информация о

нем закладывается в устройство сравнения один раз и

хранится в нем постоянно.

Шкала отношений.

Если в качестве одной из двух реперных точек выбрать

такую, в которой размер не принимается равным нулю, а

равен нулю на самом деле, то

по такой шкале можно

отсчитывать абсолютное значение размера и определять во

сколько раз один размер больше ли меньше другого. Эта

шкала называется шкалой отношений. Примером может

служить температурная шкала Кельвина. В ней за начало

отсчета принят абсолютный нуль температуры, при котором

прекращается тепловое движение молекул. Второй реперной

точкой служит температура таяния льда. По шкале Цельсия

интервал между этими реперными точками равен 273,16

0

С.

Поэтому на шкале Кельвина интервал между этими точками

делят на 273,16 частей. Каждая такая часть называется

Кельвином и равна градусу Цельсия, что облегчает переход от

одной шкалы в другую.

Шкала отношений является самой совершенной, наиболее

информативной. На ней определены все математические

действия.: сложение, вычитание, умножение и деление.

Отсюда следует, что значения любых размеров на шкале

отношений можно складывать между собой, вычитать,

перемножать и делить. Следовательно, можно определить,

насколько или во сколько раз один размер больше или меньше

другого.

В зависимости от того , на какие интервалы разбита

шкала, один и тот же размер проставляется по разному.

Например, 0,001 км; 1 м; 100 см; 1000 м – четыре варианта

представления одного и того же размера. Их называют

значениями измеряемой величины.

Устройство

сравнения

Отсчетное

устройство

83 84

Таким образом, значение измеряемой величины – это

выражение ее размера в определенных единицах измерения.

Входящее в нее отвлеченное число называется числовым

значением. Оно показывает, на сколько единиц измеряемый

размер больше нуля или во сколько раз он больше единицы

(измерения). Например, в выражениях: 5 кг; 100 гр; 20 ч; 500

т; 7 руб.; 6 баллов, числа 5, 100, 20, 500, 7, 6 являются

числовыми значениями величин: кг, гр, ч, т, руб., балл.

Значение измеряемой величины Q определяется ее

числовым значением g м некоторым размером

[

]

Q

,

принятым за единицу измерения:

[]

QgQ =

. (53)

где Q – измеряемая величина;

[]

Q

- единица измерения;

g – числовое значение.

Выражение (53) называется основным уравнением

измерения.

Увеличение или уменьшение

[

]

Q

влечет за собой

обратно пропорциональное изменение g . Поэтому значение

как и размер измеряемой величины от выбора единиц

измерения не зависит.

Абсолютные шкалы. Они обладают всеми свойствами

шкал отношений. Единицы абсолютных шкал естественны, а

не выбраны по соглашению, но эти единицы безразмерны

(разы, проценты, доли, полные углы и т. д.). Единицы

величин, описываемые абсолютными, не являются

производными единицами СИ, так как по определению

производные единицы не могут быть безразмерными. Это

внесистемные единицы. Стерадиан и радиан – это типичные

единицы абсолютных шкал. Абсолютные шкалы бывают

ограниченными и неограниченными.

Ограниченные шкалы – это, обычно, шкалы с диапазоном

от нуля до единицы (КПД, коэффициент поглощения или

отражения и т. п.). Примерами неограниченных шкал

являются шкалы, на которых измеряются коэффициенты

усиления, ослабления и т. п.

Эти шкалы принципиально нелинейны. Поэтому они не

имеют единиц измерений

3.3 Способы определения весовых коэффициентов

В зависимости от измерительной задачи разработаны

различные алгоритмы определения весовых коэффициентов.

Анализ существующих способов определения весовых

коэффициентов показывает, что наибольшее распространение

получили три способа: способ ранжирования, способ

попарного сопоставления и способ двойного попарного

сопоставления. Они отличаются как подходами к постановке

вопросов, на которые отвечают эксперты, так и проведением

экспериментов и обработкой результатов экспертиз.

Способ ранжирования. Представление результата

измерения ранжированным рядом имеет смысл тогда, когда

несколько объектов экспертизы можно рассматривать как

один составной объект той же природы. Порядок действий

при этом бывает следующий.

1. Объекты экспертизы располагаются в

порядке их предпочтения (ранжирование). Место, занятое при

такой расстановке в ранжированном ряду, называется рангом.

2. Наиболее важному, по мнению эксперта,

объекту экспертизы приписывается наибольший балл, всем

остальным в порядке уменьшения их относительной

значимости – баллы до 1.

3. Полученные результаты измерений

нормируют, т.е. делят на общую сумму баллов. Полученные,

85 86

таким образом, весовые коэффициенты принимают значения

от 0 до 1, а их сумма становится равной 1.

Значения весовых коэффициентов в таком случае

рассчитываются по формуле:

∑∑

∑

==

=

n

i

ji

m

j

n

i

ji

j

G

g

1

,

1

,

(54)

где

ji

G

,

- балл (ранг) j-го показателя, проставленный i-ым

экспертом;

n - количество экспертов;

m - количество «взвешиваемых» показателей.

При обработке результатов экспертиз, полученных

ранжированием необходимо выполнить следующие операции:

1) определить сумму баллов, проставленных всеми

экспертами j-му объекту экспертизы (показателю);

2) определить сумму баллов всех объектов экспертизы

(показателей), проставленных всеми экспертами;

3) определить весомость или весовой коэффициент j-го

объекта экспертизы (показателя).

Пример. 5.

Мнения пяти экспертов о семи объектах экспертизы выражены

следующим образом:

первый эксперт:

7461235

QQQQQQQ

〈

〈〈

〈

второй эксперт:

7146235

QQQQQQQ

〈

〈〈

〈

третий эксперт:

7461523

QQQQQQQ

〈

〈〈

〈

четвертый эксперт:

7641235

QQQQQQQ

〈

〈〈

〈

пятый эксперт:

7462135

QQQQQQQ

〈

.

По сумме рангов каждого объекта экспертизы построить

ранжированный ряд, являющийся результатом многократного

измерения.

Определить весомость членов ряда.

Решение.

1. Сумма рангов

Q

1

равна 4 + 6 + 4 + 4 + 3 = 12;

Q

2

равна 3 + 3 + 2 + 3 + 4 = 15;

Q

3

равна 2 + 2 + 1 + 2 + 2 = 9;

Q

4

равна 6 + 5 + 6 + 5 + 6 = 28;

Q

5

равна 1 + 1 + 3 + 1 + 1 = 7;

Q

6

равна 5 + 4 + 5 + 6 + 5 = 25;

Q

7

равна 7 + 7 + 7 + 7 + 7 = 35.

Результат многократного измерения имеет вид:

7461235

QQQQQQQ

〈

2. По формуле (1):

15,0

140

21

1

==g ; 11,0

140

15

2

==g ; 06,0

140

9

3

==g ;

2,0

140

28

4

==g ; 05,0

140

7

5

==g ; 18,0

140

25

6

==g ;

25,0

140

35

7

==g ;

∑

=

7

1

j

g

Способ попарного сопоставления. При этом способе

эксперт получает матрицу, в которой по вертикали и

горизонтали проставлены номера объектов экспертизы

(показателей качества). Эксперту необходимо проставить в

87 88

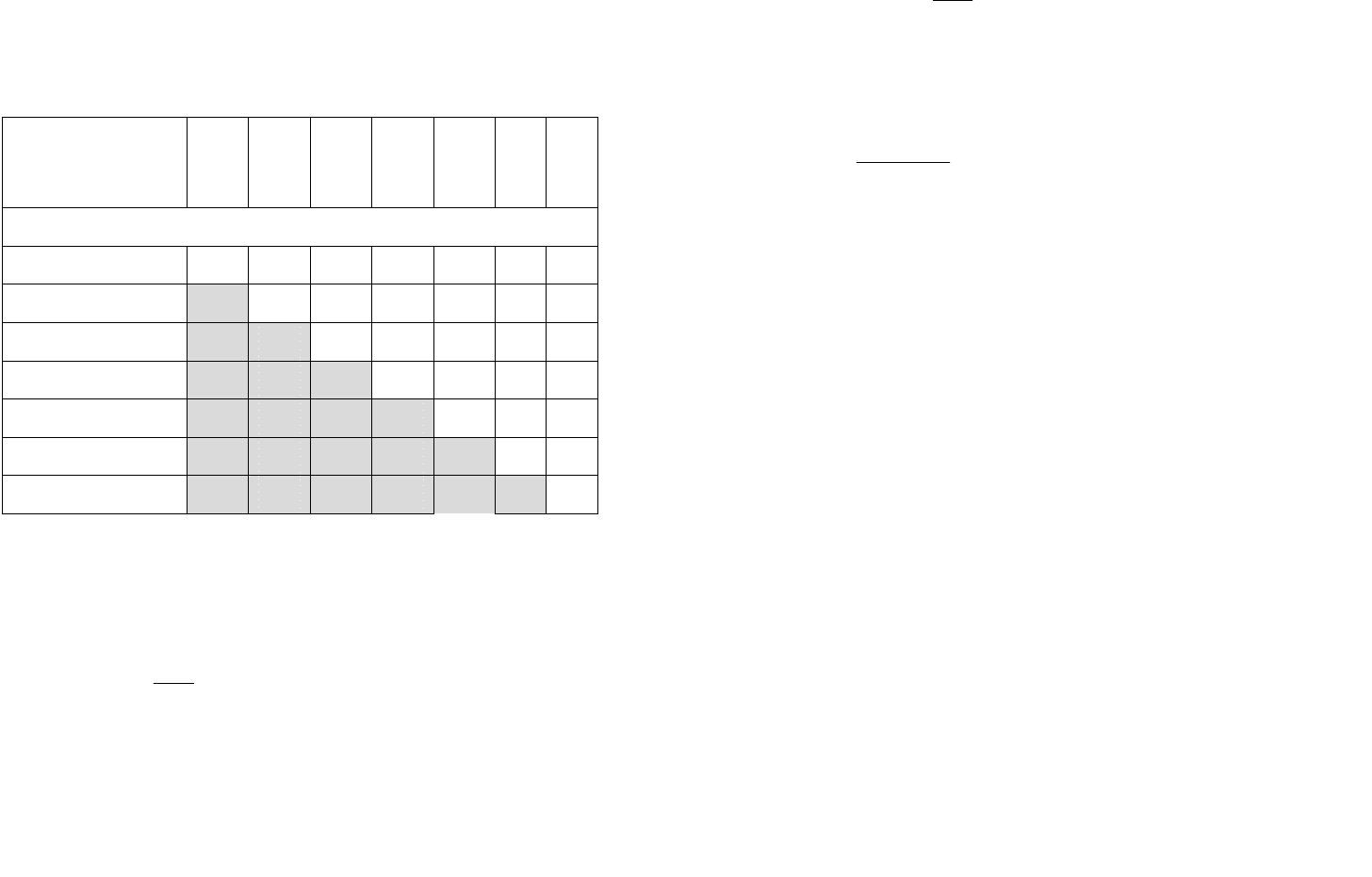
каждой клетке, относящейся двум сравниваемым объектам

(показателям), номер того объекта (показателя), который он

считает наиболее важным так, как это показано в табл. 3.

Таблица 3.

При попарном сопоставлении используется только

верхняя часть таблицы. Расчет весовых коэффициентов

производится по формуле:

∑

=

n

i

ij

j

n

F

g

1

(55)

где

ji

F

,

- частота предпочтения i–ым экспертом j-го

объекта экспертизы, определяемая как:

C

K

F

ij

ji

=

,

(56)

K

i,j

– число предпочтений i–ым экспертом j-го объекта

экспертизы;

С - общее число суждений одного эксперта, связанная с

числом объектов экспертизы m соотношением:

2

)1(

−

=

mm

C

(57)

При обработке квалиметрической информации,

полученной попарным сопоставлением, порядок действий

будет выглядеть следующим образом:

- определение числа предпочтения i-ым экспертом j-го

объекта экспертизы К

i,j

;

- определение числа суждений одного эксперта -С;

- определение частоты предпочтения i-ым экспертом j-го

объекта экспертизы F

i,j

;

- определение частоты предпочтения всеми экспертами j-

го объекта экспертизы

∑

=

n

i

ji

F

1

,

;

-

определение весомости или весового коэффициента j-

го объекта экспертизы, по мнению всех экспертов – g

j

.

Пример. 6. Мнения четырех экспертов о шести объектах

экспертизы выражены следующим образом, как это показано в

таблицах 4-7.

По сумме предпочтений каждого объекта экспертизы

построить ранжированный ряд, являющийся результатом

многократного измерения.

Определить весомость членов ряда.

Номера

объектов

экспертизы

1 2 3 4 5 6 7

1-ый эксперт

1 Х 1 2 1 1 1 1

2 Х 3 2 2 2 2

3 Х 3 3 3 3

4 Х 5 6 4

5 Х 6 7

6 Х 6

7 Х

89 90

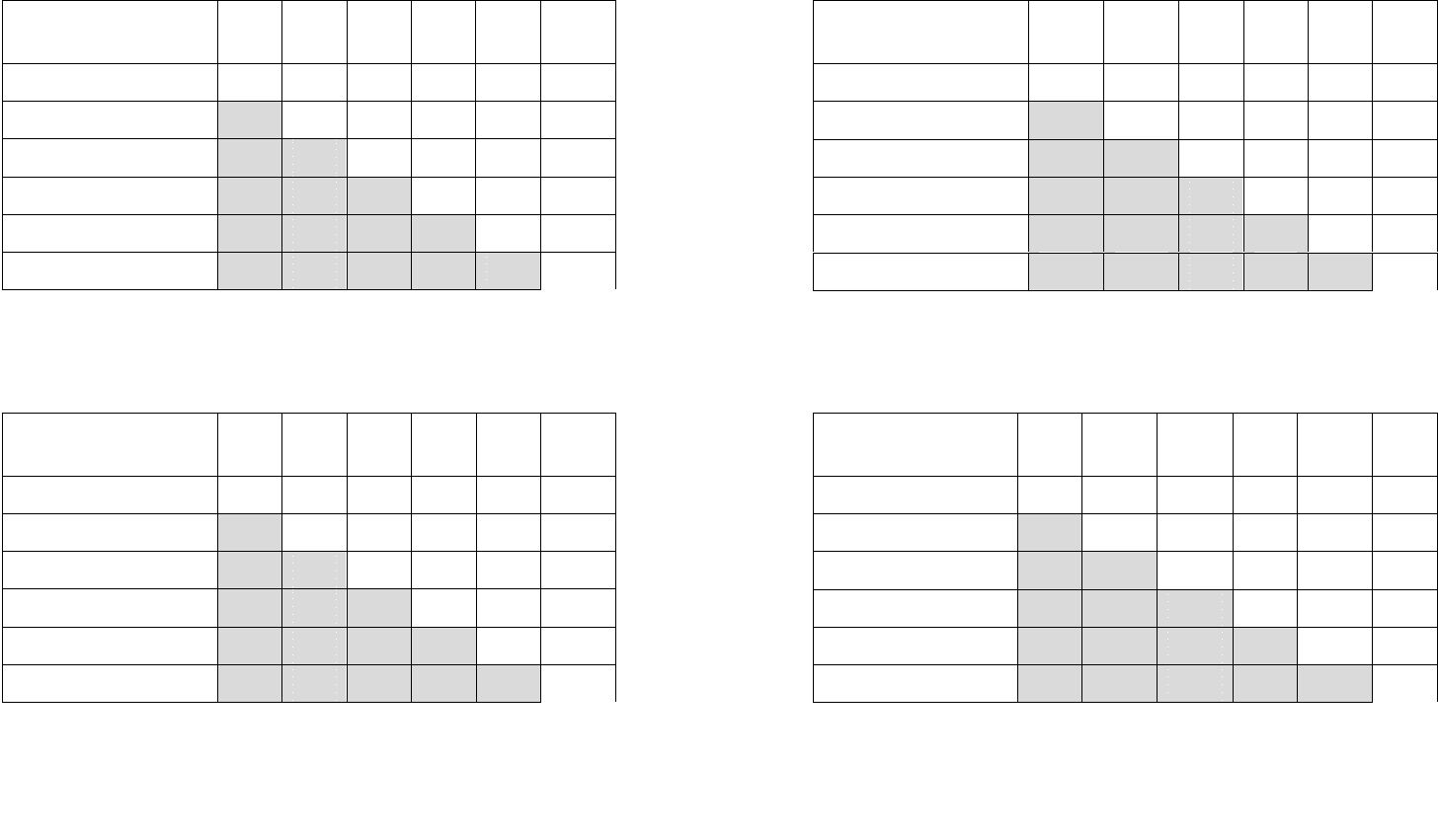
Таблица 4 Мнение первого эксперта

Таблица 5 Мнение второго эксперта

Таблица 6 Мнение третьего эксперта

Таблица 7 Мнение четвертого эксперта

Номера объектов

экспертизы

1 2 3 4 5 6

1 Х 1 1 1 1 1

2 Х 3 4 2 2

3 Х 3 3 3

4 Х 5 6

5 Х 6

6 Х

Номера объектов

экспертизы

1 2 3 4 5 6

1 Х 1 1 1 1 1

2 Х 3 2 2 2

3 Х 3 3 3

4 Х 5 4

5 Х 6

6 Х

Номера объектов

экспертизы

1 2 3 4 5 6

1 Х 1 3 1 1 1

2 Х 3 4 2 2

3 Х 3 3 3

4 Х 5 6

5 Х 6

6 Х

Номера объекта

экспертизы

1 2 3 4 5 6

1 Х 1 3 1 1 1

2 Х 3 2 2 2

3 Х 3 3 3

4 Х 5 6

5 Х 6

6 Х

91 92

Решение.

1. Число предпочтений i–ым экспертом j-го объекта

экспертизы:

K

1,1

= 4; K

2,1

= 4; K

3,1

= 5; K

4,1

= 5;

K

1,2

= 3; K

2,2

= 2; K

3,2

= 2; K

4,2

= 3;

K

1,3

= 5; K

2,3

= 5; K

3,3

= 4; K

4,3

= 4;

K

1,4

= 0; K

2,4

= 1; K

3,4

= 1; K

4,4

= 1;

K

1,5

= 1; K

2,5

= 1; K

3,5

= 1; K

4,5

= 1;

K

1,6

=2; K

2,6

= 2; K

3,6

= 2; K

4,6

= 1.

2. Общее число суждений одного эксперта

15

2

)16(6

2

)1(

=

−

=

−

=

mm

C

3. Частота предпочтения i-ым экспертом j-го объекта

экспертизы F

i,j

15

4

1,1

=F

;

15

4

1,2

=F

;

15

5

1,3

=F

;

15

5

1,4

=F

;

15

3

2,1

=F

;

15

2

2,2

=F

;

15

2

2,3

=F

;

15

3

2,4

=F

;

15

5

3,1

=F

;

15

5

3,2

=F

;

15

4

3,3

=F

;

15

4

3,4

=F

;

15

0

4,1

=F

;

15

1

4,2

=F

;

15

1

4,3

=F

;

15

1

4,4

=F

;

15

1

5,1

=F

;

15

1

5,2

=F

;

15

1

5,3

=F

;

15

1

5,4

=F

;

15

2

6,1

=F

;

15

2

6,2

=F

;

15

2

6,3

=F

;

15

1

6,4

=F

.

4. Весовой коэффициент j-го объекта экспертизы, по

общему мнению всех экспертов

30

9

15

5

15

5

15

4

15

4

1

=

⎟

⎠

⎞

⎜

⎝

⎛

+++=g

;

30

5

15

3

15

2

15

2

15

3

4

1

2

=

⎟

⎠

⎞

⎜

⎝

⎛

+++=g

;

30

9

15

4

15

4

15

5

15

5

4

1

3

=

⎟

⎠

⎞

⎜

⎝

⎛

+++=g

;

60

3

15

1

15

1

15

1

15

0

4

1

4

=

⎟

⎠

⎞

⎜

⎝

⎛

+++=g

;

30

2

15

1

15

1

15

1

15

1

4

1

5

=

⎟

⎠

⎞

⎜

⎝

⎛

+++=g

;

60

7

15

1

15

2

15

2

15

2

4

1

6

=

⎟

⎠

⎞

⎜

⎝

⎛

+++=g

.

5. Сумма рангов

1

60

7

15

1

60

3

30

9

30

5

30

9

1

=+++++=

∑

=

m

j

g

6. Ранжированный ряд объектов экспертизы имеет вид: №1;

№3; №2; №6; №5; №4. Объекты №1 и №2 равноценны.

Способ полного (двойного) попарного сопоставления

Опыт попарного сопоставления показывает, что в силу

особенностей человеческой психики эксперты иногда

бессознательно отдают предпочтение не тому объекту

экспертизы, который важнее, а тому, который стоит в

рассматриваемой паре первым. Чтобы избежать этого

проводят двойное или полное попарное сопоставление. Для

этого используют свободную часть (нижнюю) таблицы 3 и

проводят попарное сопоставление дважды.

Например,

проводят сопоставление первого объекта со вторым, третьим,

четвертым и т.д, затем второго с первым, третьим, четвертым,

… и так до последнего, а потом в обратном порядке:

последнего с предпоследним, … и до первого;

предпоследнего с последним, предыдущим, … и вновь до

первого. Таким образом, каждая пара объектов сопоставляется

дважды, причем в

разном порядке и по истечении некоторого

времени. При таком сопоставлении

93 94

иногда удается избежать случайных ошибок, кроме того

выявить экспертов, небрежно относящихся к своим

обязанностям или не имеющих определенной точки зрения.

Иначе говоря, двойное попарное сопоставление обладает

более высокой надежностью, чем однократное Порядок

расчетов остается прежним, за исключением

)1(

−

= mmC

(58)

При обработке результатов экспертиз, полученных

двойным попарным сопоставлением, выполняются те же

операции, что при попарном сопоставлении, за исключением

того, что число суждений одного эксперта определяется по

формуле 58. Кроме перечисленных выше способов

определения весовых коэффициентов выделяют: способ

предпочтения, второй способ попарных сопоставлений и

способ последовательных сопоставлений.

3.4 Способы уточнения весовых коэффициентов

Уточнить результаты измерений или значения весовых

коэффициентов, полученных попарным сопоставлением,

можно методом последовательного приближения.

Первоначальные результаты рассматриваются в этом случае

как первое приближение. Во втором приближении они

используются как весовые коэффициенты

)2(

j

G

суждений

экспертов. Полученные с учетом этих весовых коэффициентов

новые результаты в третьем приближении рассматриваются

опять как весовые коэффициенты

)3(

j

G

тех же мнений

экспертов и т.д. Согласно теореме Перрона-Фробениуса, при

определенных условиях, которые

на практике выполняются, этот процесс сходится, т.е.

нормированные результаты измерений

j

g

или весовые

коэффициенты стремятся к некоторым постоянным значениям

строго отражающим соотношения между объектами

экспертизы при установленных экспертами исходных данных.

Первый способ уточнения весовых коэффициентов

методом последовательного приближения

Первый способ уточнения весовых коэффициентов

основан в определении весовых коэффициентов в (ω)

приближении как среднее арифметическое взвешенное.

В случае обозначении предпочтений эксперта через

ij

K

,

, первоначальные результаты

(

)

1

j

G

будут

определяться формулой:

()

∑

=

m

i

jiJ

KG

1

(59)

где

ij

K

,

- число предпочтений j-го объекта одним

экспертом;

(

)

1

j

G

- результат измерения j-го объекта в первом

приближении.

А результаты измерения в (ω) приближении будут равны:

()

(

)

(

)

(

)

ϖ

jmjjJ

KGKGKGG

⋅

−

+

⋅

−

+

⋅

−

=

1...11

2211

(60)

где

(

)

1

−

ω

j

G

- результат измерения j-го объекта в (ω)

приближении.

Очевидно, что значения весовых коэффициентов в ω

приближении, определяемые как

()

(

)

()

∑

=

m

j

J

G

g

1

ϖ

(61)

95 96

будут значительно отличаться от значения весовых

коэффициентов в 1-ом приближении.

В ходе уточнения все более подчеркивается

предпочтительность одного и низкая значимость другого

показателя. Процесс уточнения значений продолжается до тех

пор, пока точность не достигнет заданной, т.е. пока не

выполнится условие:

()

(

)

εωω

≤−− 1

jj

gg

,

где

ε

- заданная точность вычислений.

Пример 7. Результаты полного попарного сопоставления

одним экспертом пяти объектов экспертизы представлены в

таблице 8 где предпочтение j-го объекта перед i-м обозначено

цифрой 2, равноценность – цифрой 1, а предпочтение i-го объекта

перед j-м – цифрой 0.

Что можно сказать о результате измерения в третьем

приближении? На сколько отличаются весовые коэффициенты в

первом и третьем приближениях?

Таблица

8

ш

1 2 3 4 5

(

)

1

j

G

()

1

j

g

()

2

j

G

(

)

2

j

g

(

)

3

j

G

(

)

3

j

g

1 1 2 2 1 2 8 0,32 36 0,395 124 0,435

2 0 1 2 2 2 7 0,28 27 0,297 83 0,291

3 0 0 1 0 0 1 0,04 1 0,011 1 0,004

4 1 0 2 1 1 6 0,24 22 0,242 70 0,246

5 0 0 2 0 0 3 0,12 5 0,055 7 0,024

25 1,00 91 1,00 285 1,00

Решение. 1.

В первом приближении:

(

)

()

3102001

6212011

1001001

7222101

8212211

5

4

3

2

1

=++++=

=

+

=

G

2. Во втором приближении:

3. В третьем приближении:

.

4. Значения

j

g

, приведенные в таблице 7, заметно

отличаются в первом и третьем приближении. С каждым

следующим приближением они будут уточняться. В ходе уточнения

все более подчеркивается предпочтительность первого объекта

экспертизы и низкая значимость третьего (в меньшей мере –

пятого).

(

)

()

513062107082

3223162107182

123061107082

2723162117082

3623162127182

5

4

3

2

1

=⋅+⋅+⋅+⋅+⋅=

=

⋅

+

⋅

+

⋅

+

⋅

+

⋅

=

G

()

715022210270363

7025122210271363

125022110270363

8325122211270363

12425122212271363

5

4

3

2

1

=⋅+⋅+⋅+⋅+⋅=

=

⋅

+

⋅

+

⋅

+

⋅

+

⋅

=

G

97

98

Хамханова Д.Н. Основы квалиметрии

Подождите немного. Документ загружается.