Хамханова Д.Н. Основы квалиметрии

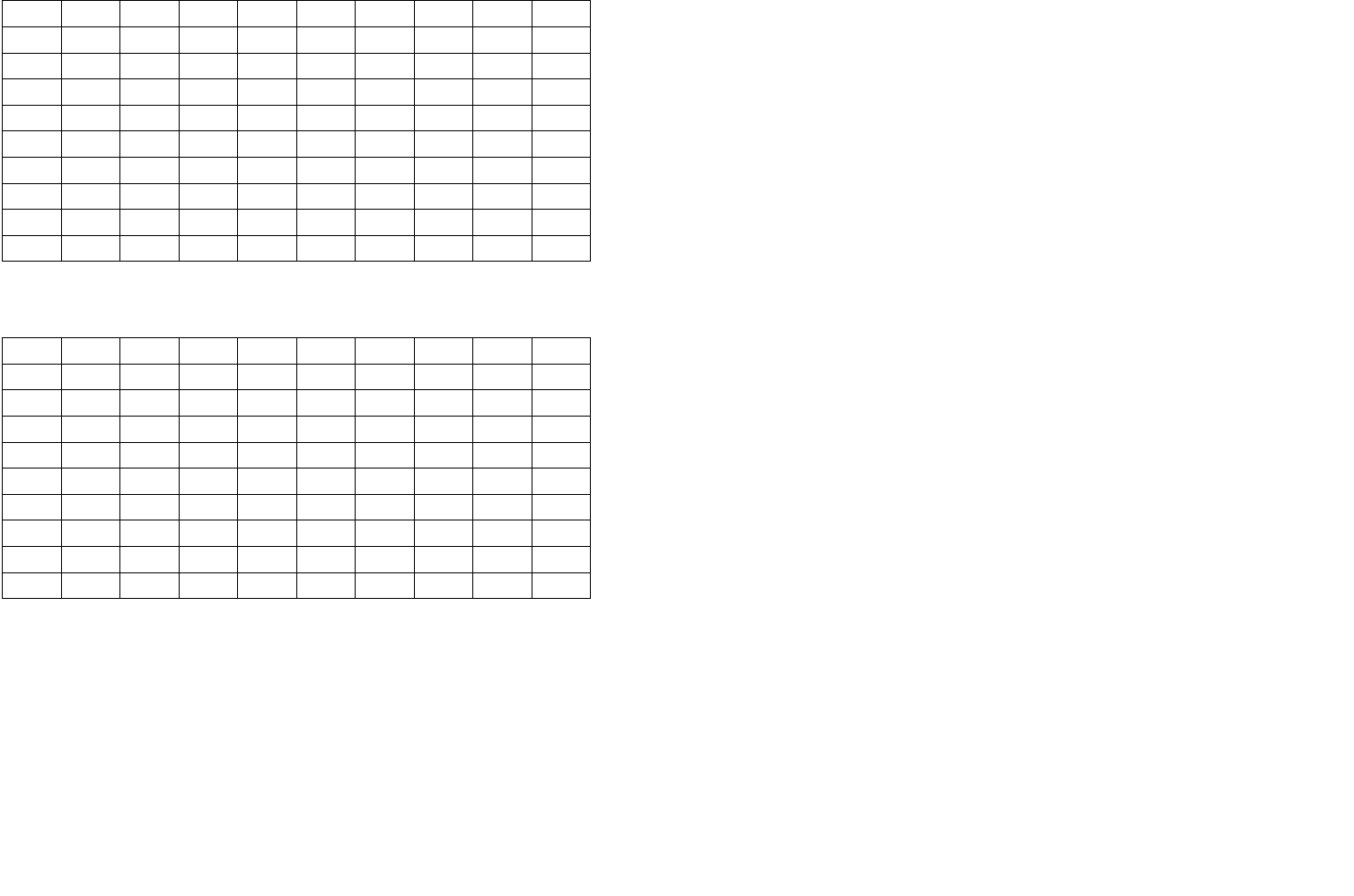
в)

г)

Рис.8 Графическое двумерное представление

средневзвешенных комплексных показателей качества: а)

гармонического; б) арифметического; в) геометрического; г)

квадратического.

Комплексный средневзвешенный показатель качества,

например

Q

ˆ

, можно представить точкой А (см. рис. 8) с

координатами

)(

2,1 AA

QQ

, рядом с которой указано в

скобках числовое значение этого показателя (0,55). Точки,

имеющие одинаковое числовые значения комплексного

показателя (например,

)

ˆ

( constQ =

, можно соединить

между собой и получить линию равного качества,

изоквальную линию, кратко изоквалиту (гр. isos – равный,

лат. gualis – какой по качеству). Тогда внутри квадрата,

ограниченного осями координат и линиями, проходящими

параллельно осям координат через точки (0,1) и (1,0),

можно построить сетки изоквальных линий (изоквалит) для

разных средневзвешенных: гармонического,

геометрического, арифметического и квадратического.

На каждой

изоквалите указаны числовые значения

комплексного показателя качества. Чем дальше от начало

координат находится изоквалита, тем больше числовые

значения комплексных показателей качества. Сетки

изоквалит для разных средневзвешенных можно наложить

друг на друга. Фрагмент такого наложения изоквалит для

разных средневзвешенных, имеющих одно и то же значение

комплексного показателя качества представлен на рис. 9. В

точках, расположенных на главной диагонали (А1 на рис. 9)

квадрата

max2max1

0 QQQ −−−

)

, изоквалиты,

имеющие одинаковое значение показателя, сходятся. Таким

образом, если происходит комплексирование равных по

значению единичных показателей качества (при любых

весах), то вид среднего взвешенного не имеет значения.

Если комплексируют разные по значению единичные

показатели, то вид среднего взвешенного имеет значение

(А2 на рис. 9).

119

120

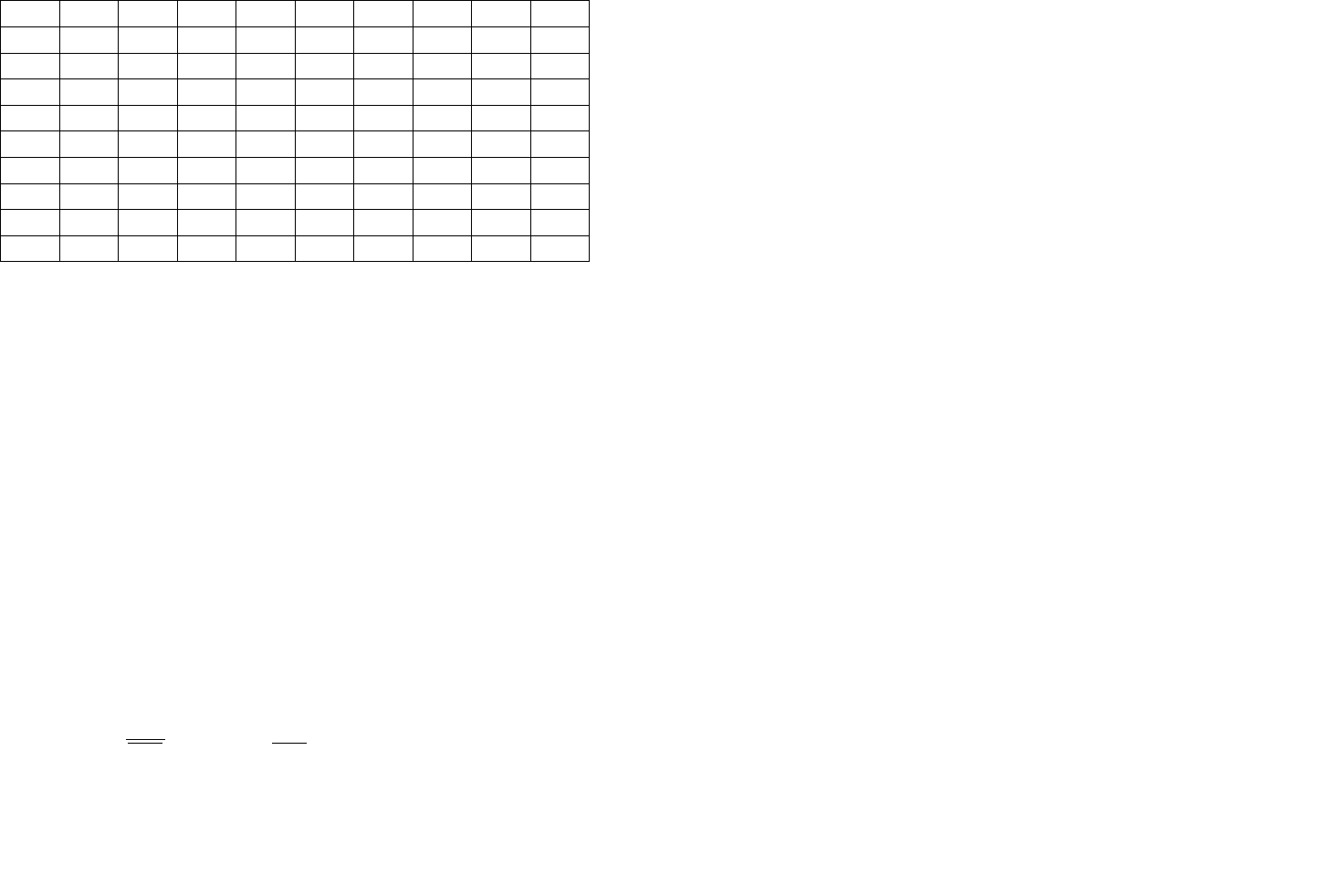
Рис.9 . Взаимосвязь средневзвешенных комплексных

показателей качества

Точка А2 отображает комплексный показатель качества

отн

Q

ˆ

, в которой были объединены единичные показатели

9,0

1

=

отн

Q

и

5,0

2

=

отн

Q

, с весами g

1

и g

2

,

обеспечивающие для

отн

Q

ˆ

значения 0,7. В данном

примере

5,0

21

=

gg

, и тогда

∑

=

=⋅+⋅=+==

2

1

2211

7,09,05,05,05,0

ˆ

m

j

отнотнjоотjотн

QgQgQgQ

.

Изоквалиты со значением

7,0=

отн

Q

)

для других

средневзвешенных проходят вне точки А2. Из рис. 9 видно,

что при заданных

отн

Q

1

и

отн

Q

2

значения разных

средневзвешенных комплексных показателей связаны

неравенством

QQQQ ∠∠∠

ˆ

~

(83)

Чтобы наглядно изобразить комплексный

средневзвешенный показатель, объединяющий три

единичных показателя, надо перейти к трехмерной

пространственной (например, прямоугольной) системе

координат (рис.10). В этом случае изоквальные линии

превращаются в изоквальные поверхности (поверхности

равного качества). Форма изоквальной поверхности зависит

от вида средневзвешенного. Например, для среднего

арифметического взвешенного это будет плоскость (рис.

10, а

), для среднего квадратического взвешенного это будет

плоскость (рис. 10, б). Комплексный средневзвешенный

показатель качества как и ранее, можно изобразить точкой

(А1, А2, …) только уже не плоскости, а в пространстве.

Координатами точки, например А1, являются значения

единичных показателей:

1

3

1

2

1

;;

отнотнотн

QQQ

.

Рядом с точкой А1 в скобках может быть указано

числовое значение комплексного показателя. Внутри куба,

ограниченного координатными плоскостями, проведенными

через максимальные значения единичных показателей

параллельно координатным плоскостям, можно построить

совокупность изоквальных поверхностей для каждого вида

средневзвешенного.

При пересечении этих изоквальных поверхностей

диагональной плоскостью, проведенной через ось Q

2

и

диагональ горизонтальной плоскости (линия

max1max2

,0 QQ⎯→←

, получится картина аналогичная

изображенной на рис. 9.

При комплексировании четырех и более показателей

дать наглядное изображение изоквальной многомерной

поверхности невозможно.

Однако взаимное расположение этих многомерных

наблюдаемых гиперповерхностей остается прежним,

остается справедливым неравенство 83.

121 122

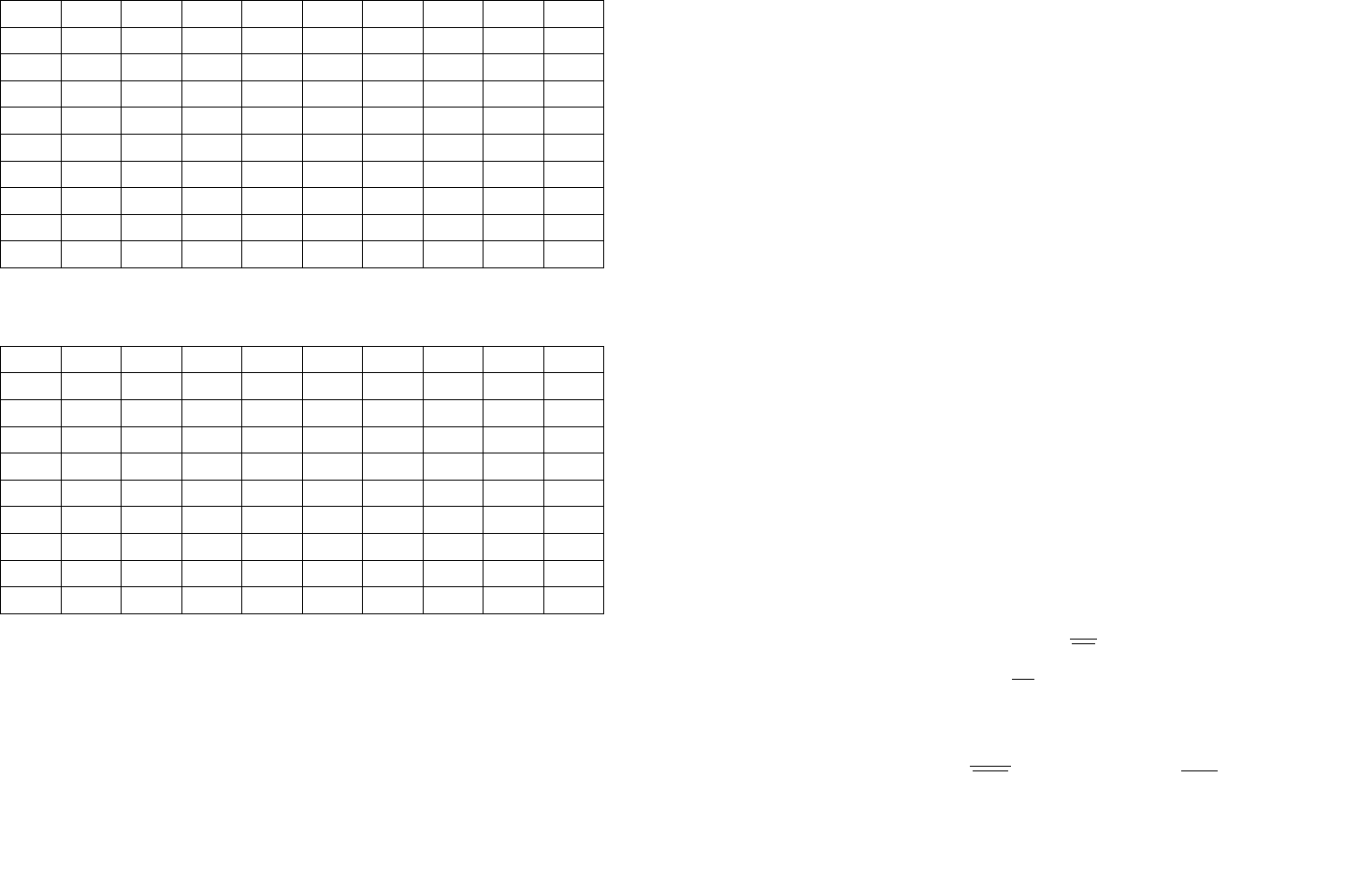
а)

б)

Рис.10. Графическое трехмерное представление

средневзвешенных комплексных показателей качества

Использовав рис.1.8, также можно наглядно показать

чувствительность средневзвешенных комплексных

показателей к изменению единичных.

Пусть точка А3 на рис. 9 характеризует комплексный

показатель качества

Q

)

. Расположение точки А3 на

главной диагонали свидетельствует о том, что комплексный

показатель качества сформирован из двух равных по

значению единичных показателей качества

1

Q

и

1

2

Q

.

Допустим, что в результате каких-то причин единичный

показатель качества

1

Q

изменился (получил приращение)

на

1

QΔ

, а единичный показатель качества

1

2

Q

остается

прежним. За счет

1

QΔ

изменится и комплексный

показатель качества

Q

)

на

Q

)

Δ

.

На рис. 9 изменение значения комплексного показателя

означает перемещение точки А3 в новое положение на

плоскости координат м переход в точку А3

1

.

Точка А3

1

соответствует новому значению

комплексного показателя

QQ

)

Δ+

. Чтобы показать на

рис. 9 значение

Q

)

Δ

, надо через точку А3 провести

изоквалиты (или следы изоквальных поверхностей),

соответствующие разным средневзвешенным. Изоквалиты

будут пересекать диагональ в соответствующих точках.

Расстояние от этих точек от точки А3 и есть приращение

комплексных показателей качества для средневзвешенных:

Q

~

Δ

- гармонического;

QΔ

- геометрического;

Q

ˆ

Δ

-

арифметического;

QΔ

- квадратического. Из рис. 9

следует, что между этими приращениями существует

неравенство

QQQQ Δ∠Δ∠Δ∠Δ

ˆ

~

, (84)

которое имеет тот же смысл, что и формула (81). Оба эти

123 124

неравенства являются следствием выбора параметра

γ

в

формуле (64).

Если разделить приращение соответствующего

средневзвешенного на приращение единичного показателя,

получим неравенство

1

ˆ

~

Q

Δ

∠

Δ

∠

Δ

∠

Δ

. (85)

Это неравество служит практической рекомендацией

при выборе вида средневзвешенного по признаку

чувствительности к изменениям единичного показателя.

Если исходная точка А3 будет находится на диагонали,

методика определения приращений

Q

)

Δ

останется

прежней. Однако и в этом случае необходимо значение

Q

)

Δ

определять на диагонали.

Обычно среднее арифметическое взвешенное

Q

ˆ

Δ

используют тогда, когда в комплексный показатель

качества объединяют однородные показатели, разброс

значений между которыми невелик;

среднее гармоническое взвешенное

Q

~

Δ

применяют,

если разброс значений между слагаемыми более

значительный;

среднее геометрическое взвешенное

QΔ

считают

наиболее универсальным и распространенным

комплексным показателем. По схеме среднего

геометрического взвешенного объединяют

(комплексируют) единичные показатели качества, когда они

неоднородны (относятся к разнородной продукции и

разным условиям его применения) и имеют значительный

разброс;

среднее квадратическое взвешенное

QΔ

используют в

методе наименьших квадратов, а также во многих других

случаях. Принципиально можно использовать любой из

них.

3.7. Чувствительность к изменениям средних

взвешенных

Субъективный характер выбора параметра логики

усреднения при образовании комплексных показателей

качества по принципу среднего взвешенного ставит вопрос

о том, какая разновидность среднего взвешенного

предпочтительнее в конкретных условиях. Это проблема не

новая. Еще в ХV11 в. шла дискуссия между Галилеем и

Кацилино о преимуществах среднего арифметического

перед средним геометрическим. Галилей отдавал

предпочтение

среднему арифметическому, а Кацилино –

среднему геометрическому. Чтобы ответить на

поставленный вопрос, выбирают ряд признаков, по

которому ведут сравнение средних взвешенных. Один из

таких признаков – чувствительность к изменениям

(приращениям значений каждого из единичных показателей

качества

j

Q

. Понятно, что чувствительность к изменениям

определяет дифференциал средневзвешенного

комплексного показателя:

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∂

∏

=

m

j

g

j

jj

j

Q

QQ

Q

1

;

ˆ

1

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∂

∑

=

m

j

jj

Qg

QQ

Q

125 126

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∂

∑

=

m

j

jj

Q

g

QQ

Q

1

~

;

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∂

∑

=

m

j

jj

Qg

QQ

Q

1

2

.

Для среднего арифметического взвешенного

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∂

∑

=

m

j

jj

Qg

QQ

Q

1

=

j

m

j

jj

j

gQgQg

Q

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅+⋅

∂

∑

≠

=

l

ll

1

(86)

чувствительность к изменениям единичного показателя

является величиной постоянной и равной весу этого

единичного показателя среди других слагаемых.

Для среднего геометрического взвешенного:

⎥

⎦

⎤

⎢

⎣

⎡

⋅

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∂

≠

==

jj

g

j

g

m

j

g

j

m

j

jj

QQП

Q

QП

QQ

Q

l

l 11

(87)

Постоянный множитель обозначим через С, равное

l

g

m

j

QПC

≠

=

1

.

Тогда формула (86) примет вид:

(

) ()

1−

⋅=

∂

=⋅

∂

=

∂

j

jj

g

j

g

j

g

j

jj

QCQ

Q

CQC

QQ

Q

(88)

Как видно из формулы (87) чувствительность к

изменениям единичного показателя среднего

геометрического взвешенного зависит от веса и от значения

этого единичного показателя.

Для среднего гармонического взвешенного

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∂

∑

=

m

j

jj

Q

g

QQ

Q

1

~

Полагая

1

~

−

= иQ

, где

∑

=

m

j

Q

g

и

1

имеем:

2

1

2

1

~

⎟

⎠

⎞

⎜

⎝

⎛

−=−=

∂

∑

=

−

m

j

Q

g

u

и

Q

,

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

∂

=

⎟

⎠

⎞

⎜

⎝

⎛

∂

=

∂

∑∑

=

−

=

m

j

jj

j

m

j

jj

Qg

QQ

g

QQ

u

1

2

1

11 −

≠

=

−−

⋅−=

⎥

⎦

⎤

⎢

⎣

⎡

⋅+⋅

∂

=

∑

jj

m

j

jj

j

QgQgQg

Q

l

ll

Следовательно,

2

1

2

1

~

⎟

⎠

⎞

⎜

⎝

⎛

=⋅⋅

⎟

⎠

⎞

⎜

⎝

⎛

+=

∂

⋅

∂

=

∂

∑∑

=

−

=

m

j

jj

m

j

jj

Q

g

Q

g

Qg

Q

g

Q

u

Q

(89)

127 128

Чувствительность к изменениям единичного показателя

среднего гармонического взвешенного также зависит от

веса и от значения этого единичного показателя.

Для среднего квадратического взвешенного

∑

=

⋅=

∂

=

∂

m

j

jj

Qg

QQ

Q

1

2

)

(90)

Здесь имеем следующую цепочку зависимостей:

∑

=

⋅==

m

j

jj

QguuQ

1

2

1

,

~

Тогда

∑

=

−

⋅⋅

==

∂

m

j

jj

Qg

u

Q

1

2

1

2

1

2

1

~

,

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

∂

=

∂

∑

=

m

j

jj

Qg

QQ

u

1

2

jj

m

j

jj

j

QgQgQg

Q

⋅=

⎟

⎠

⎞

⎜

⎝

⎛

⋅+⋅

∂

=

∑

≠

=

2

1

22

l

ll

Подставив полученные выражения в формулу (90)

окончательно получим:

2

1

2

~

∑

=

⋅

=

∂

⋅

∂

=

∂

m

j

jj

Qg

Q

u

Q

(91)

В этом случае чувствительность к изменениям

единичного показателя является также функцией от веса и

от значения этого единичного показателя. В общем случае

чувствительность к изменениям единичных показателей

является функцией

()

jj

j

Qgf

Q

,=

∂

)

.

Чтобы показать различие средневзвешенных по

чувствительности к изменению единичных показателей

построим графики зависимости чувствительности к

изменению единичных показателей средневзвешенных от

этого изменения. Допустим, что в комплексный показатель

объединены пять единичных показателей

,35,0,4,0,5,0,7,0,9,0

54321

=

отнотнотнотнотн

QQQQQ

с

весами

54321

,,,, gиgggg

. В данном

примере

2,0

54321

=

ggggg

и тогда

комплексные средневзвешенные показатели равны:

5

7

,02,035,02,04,02,05,02,07,02,09,0

ˆ

1

=⋅+⋅+⋅+⋅+⋅==

∑

=

m

j

jjотн

QgQ

;

60

5

,035,02,04,02,05,02,07,02,09,02,0

ˆ

22222

1

2

=⋅+⋅+⋅+⋅+⋅==

∑

=

m

j

jjотн

QgQ

;

∏

=

=++++==

m

j

g

jотн

j

QQ

1

2,02,02,02,02,0

424,435,04,05,07,09,0

ˆ

;

505,0

979,1

1

35,0

2,0

4,0

2,0

5,0

2,0

7,0

2,0

9,0

2,0

11

ˆ

1

==

++++

==

∑

=

m

j

отн

Q

g

Q

.

130 129

Также допустим, что единичный показатель

отн

Q

5

получает приращение

9,0...35,0

5

=∂Q

.

На рис. 11 показано зависимость чувствительности

средневзвешенных от изменения единичного показателя

качества.

Рис. 11. Зависимость чувствительности средневзвешенных

комплексных показателей от приращения единичных показателей

Из полученных зависимостей видно, что для

средневзвешенных остается справедливым неравенство 84.

3.8 Многоуровневая структура показателей качества

Комплексные показатели качества, как и производные

физические величины, можно и дальше комбинировать

между собой, добиваясь все большего и большего

обобщения свойств, формулирующих в целом

представление о качестве объекта и представить в виде

иерархической структуры дерева качества (рис. 12).

В многоуровневой структуре показателей качества на

самом низком уровне располагаются единичные показатели

качества,

характеризующие одно свойство продукции.

Комплексные показатели низкого уровня образуются по

функциональной зависимости или по принципу среднего

взвешенного. Принципы формирования комплексных

показателей более высокого уровня такие же, как на

нижнем уровне. Комплексные показатели качества,

относящиеся к определенной группе, называются

групповыми. Понятие групповой показатель достаточно

условно. Так, например, физико-химические показатели

хлебобулочных изделий

можно считать групповым.

Обобщенный показатель относится к такой

совокупности свойств продукции, по которой оценивается

качество продукции. При экономических расчетах в роли

обобщенного показателя выступает интегральный

показатель.

Правила квалиметрии выработала некоторые правила

построения структуры показателей качества. Условно эти

правила делятся на общие и частные. К общим правилам

относят такие, как деление

по равному основанию,

исключительность, корректируемость, учет взаимосвязей в

системе «человек – среда – объект», жесткость структуры

начальных уровней дерева, потребительская и

функциональная направленность формулировок

131 132

,

показателей качества на любом уровне, необходимость и

достаточность числа свойств в комплексе, однозначность

толкования показателей качества, недопустимость

включения в комплексный показатель зависимых

единичных показателей качества, одновременность

существования единичных показателей качества,

включаемых в комплексный, и др. к частным правилам

относят такие показатели, как учет затрат и

результатовясность признака

деления, минимум единичных

показателей в комплексном, исключение одинаково

выраженных показателей и др.

Структура показателей качества в форме

иерархического дерева не единственная. Различают и

другие формы графического представления структуры

показателей качества в виде дерева (рис. 13),

квалификационной таблицы (рис. 14) и строгого графа (рис.

15).

Рис. 13. Дерево качества

Рис.12 Многоуровневая структура показателей качества

133

134

1

2

3

13

4

5

6

7

17

14

8

9

18

15

10

11

19

16

12

Рис. 14. Структура показателей качества в виде

квалификационной таблицы

Пример 11 На рис. 16. показана трансформация

комплексного показателя качества «функциональность здания

столовой» с учетом вышеперечисленных правил. «Дерево» а

содержит комплексные показатели, скомбинированные из

единичных показателей, имеющих разные классификационные

признаки. Поскольку всякое дерево показателей качества

является частным случаем классификации, ошибочность дерева в

том, что здесь нарушен принцип деления (классификации) по

равному основанию(единому

признаку для всех показателей

качества, объединенных в групповой). Чтобы соблюсти этот

принцип (правило),надо заменить «дерево» а «деревом» б.

1

2

13

3

4

17

5

18

6

14

7

8

9

15

10

11

16

12

Рис. 15. Структура показателей качества в виде строго графа

135

136

а)

в)

Рис.16 Трансформация комплексного показателя

3.9 Зависимость показателей качества от времени

Показатели качества, как и физические величины

меняются со временем. В одних случаях этим изменением

можно пренебречь, а в других – нельзя. Например, качество

продукции снижается к концу службы, причем в течение

этого периода могут быть интервалы, когда продукция

снята с эксплуатации из – за неисправностей, на ремонт или

техобслуживание. Эти обстоятельства учитывают

показатели

надежности (безотказность, долговечность,

ремонтопригодность, сохраняемость и др.) Показатели

надежности по своей природе в корне отличаются от других

показателей качества. Суть этого отличия хорошо поясняет

афоризм, часто приводимый в литературе: «надежность –

качество развернутое во времени» Каждый из указанных

выше показателей надежности можно выразить через

соответствующие интервалы времени, либо через

вероятность наступления

состояния, характеризуемое

показатели качества. Временное содержание показателей

надежности, а также их тесная взаимосвязь с другими

показателями, такими как показатели назначения, не

позволяет оперировать с ними, как с другими показателями

при комплексировании. Так, показатели надежности нельзя

включать в формулы средневзвешенных. Их влияние на

комплексный показатель учитывается особо.

Совершенно другое дело с остальными

показателями,

как эстетические и эргономические. Ускоренные темпы

научно - технического прогресса позволяют с каждым

годом совершенствовать производство и выпускать все

новые и новые виды аналогичной продукции с более

совершенными параметрами, кроме того на эстетические

показатели влияние оказывает мода. Так, например, с

каждым годом выпускаются новые поколения компьютеров,

137

138

Хамханова Д.Н. Основы квалиметрии

Подождите немного. Документ загружается.