Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.


270
APPENDIX
For the case of a load varying linearly in the y direction, the resultant force on the area
is the load intensity at the centroid times the area,
W=
w1y&4
This acts at the point
(x;,
y
k)
where:
In these expressions the axis Ox must be the line of zero load and the axis
Oy
'is
any
axis
normal to Ox:
A
similar analysis may be made for a
load
which varies linearly in the
x
direction and is
constant in the y direction,
Oy
'
being the
axis
of zero load. Such
a
load would have
a
resultant:
W=
w1xLA
acting at
(x;,
y
K)
where:
The second moment
I
,is given by:
YP
Iy,y.
=
Jx'%k2yf
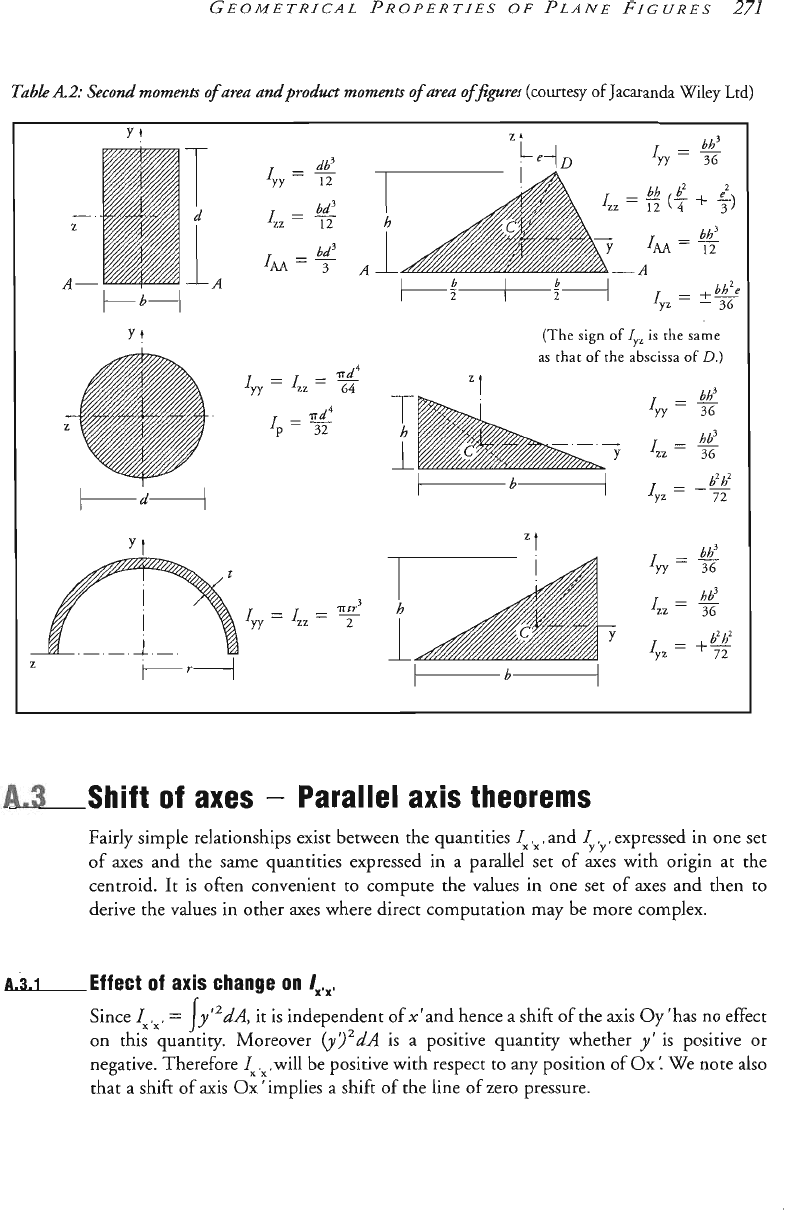
The second moments of area and product moment of area of some simple shapes are
given in Table
A.2.
GEOMETRICAL PROPERTIES
OF
PLANE
FIGURES
271
a.
T
A-
I,
2
(The
sign
of
lyz
is the same
as that
of
the abscissa
of
D.)
Fairly simple relationships exist between the quantities
,,,
and
Iy
expressed in one set
of axes and the same quantities expressed in a parallel set of axes with origin at the
centroid.
It
is often convenient to compute the values in one set of axes and then to
derive the values in other axes where direct computation may be more complex.
'X'
Since
I,
,,,
=
/yf2dA,
it is independent of x'and hence a shift of the axis Oy 'has no effect
on this quantity. Moreover
(jy2dA
is a positive quantity whether
y'
is positive or
negative. Therefore
I,
,,
,will be positive with respect to any position of Ox We note also
that a shift of axis Ox 'implies a shift of the line of zero pressure.

*X
Figwe
A.
10
Figure
A.
10
shows
a
typical element of area
dA
at distance
y
from axis
x
Its distance
from the parallel axis
Cx
through the centroid is
y,
hence:
Y1= Y
+
Y;:
The second moment of area about
Cx
is:
I,,
=
/y2dA
The second moment of area about
Ox
'is:
Now:
IXx
=
/YdA; /yd.
is
the first moment of
A
about the axis
Cx
through the
centroid and is therefore zero; and
/dA
is the area
A.
Hence:
Ixk,
=
In
+
(
Y~)~A
The term
(
Y;J)~A
is positive whether
y;:
is positive or negative. Therefore the second
moment of area about an axis through the centroid is less than that about any other
parallel axis.
Equation
A.26
is
often called the
Theorem
o~~~r~ZZeZ~e~.
It enables us to re-state
Equation
A.
16
in a more convenient form. From Equation
A.
16,
we have:
I,*,*
yK=y;:A
and using Equation
A.26:
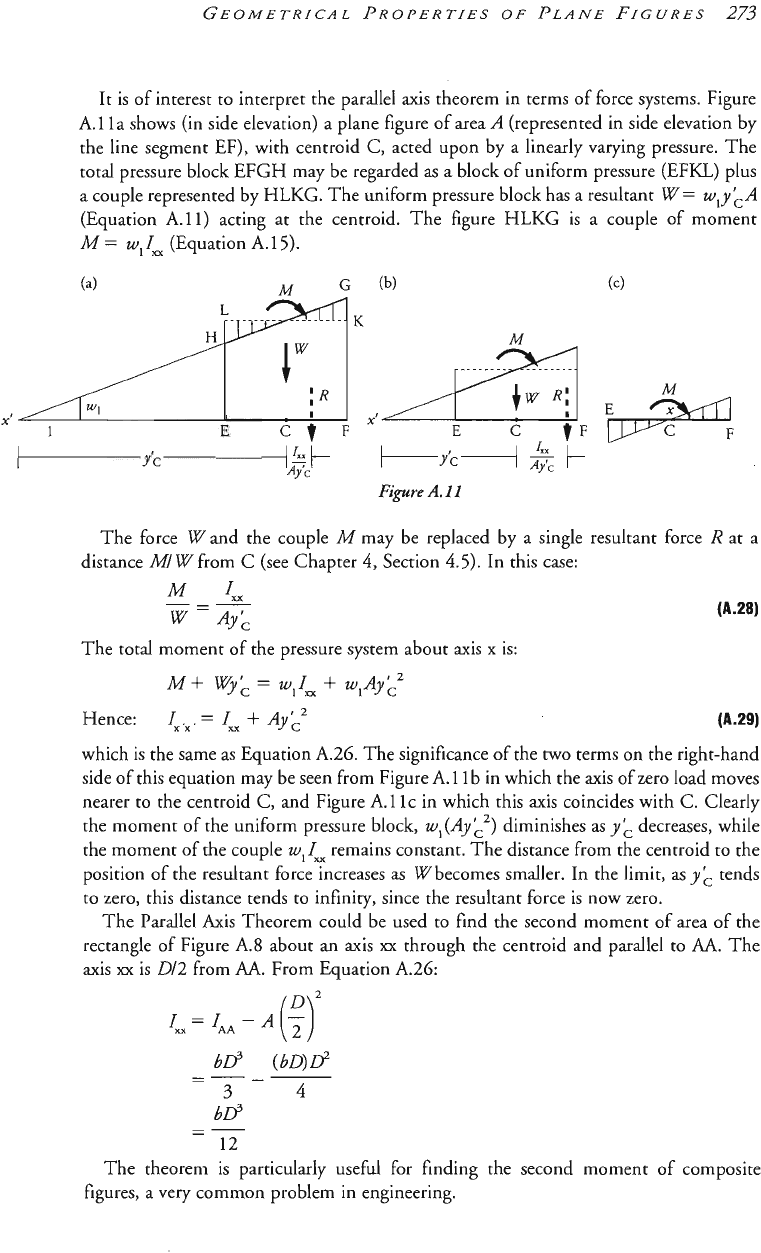
It is of interest to interpret the parallel axis theorem in terms of force systems. Figure
A,
l
la shows (in side elevation) a plane figure
of
area
A
(represented in side elevation by
the line segment
EF),
with centroid C, acted upon by a linearly varying pressure. The
total pressure block EFGH may be regarded as a block of uniform pressure
(EFKL)
plus
a couple represented by
HLKG,
The uniform pressure block has a resultant
W
=
wIy LA
(Equation
A.1
1) acting at the centroid. The figure
HLKG
is a couple of moment
M
=
w1
I,
(Equation A. 15).
K
M
X'
Fipre
A.
l l
The force
W
and the couple
M
may be replaced by a single resultant force
R
at a
distance
M/
W
from
C
(see Chapter
4,
Section
4.5).
In this case:
The total moment of the pressure system about axis
x
is:
M+ Wy;:
=
w,Ixx
+
w,AyL2
which
is
the same as Equation A.26. The significance of the
two
terms on the right-hand
side of this equation may be seen from Figure
A.
1
1
b
in which the axis of zero load moves
nearer to the centroid
C,
and Figure A.
l
IC in which this axis coincides with
C.
Clearly
the moment of the uniform pressure block,
w1
(Ay
L2)
diminishes
as
y
decreases, while
the mom~nt of the couple
w,Ixx
remains constant. The distance from the centroid to the
position of the resultant force increases as Wbecomes smaller. In the limit, as
y;:
tends
to zero, this distance tends to infinity, since the resultant force is now zero.
The Parallel Axis Theorem could be used to find the second moment
of
area
of
the
rectangle of Figure
A.8
about an axis
xx
through the centroid and parallel to
M.
The
axis
xx
is D/2 from
M.
From Equation A.26:
The
figures,
bd
(&l)@
3
4
bd
"
-
-
-
--
-
12
theorem is particularly useful for finding the second moment of composite
a very common problem in engineering.
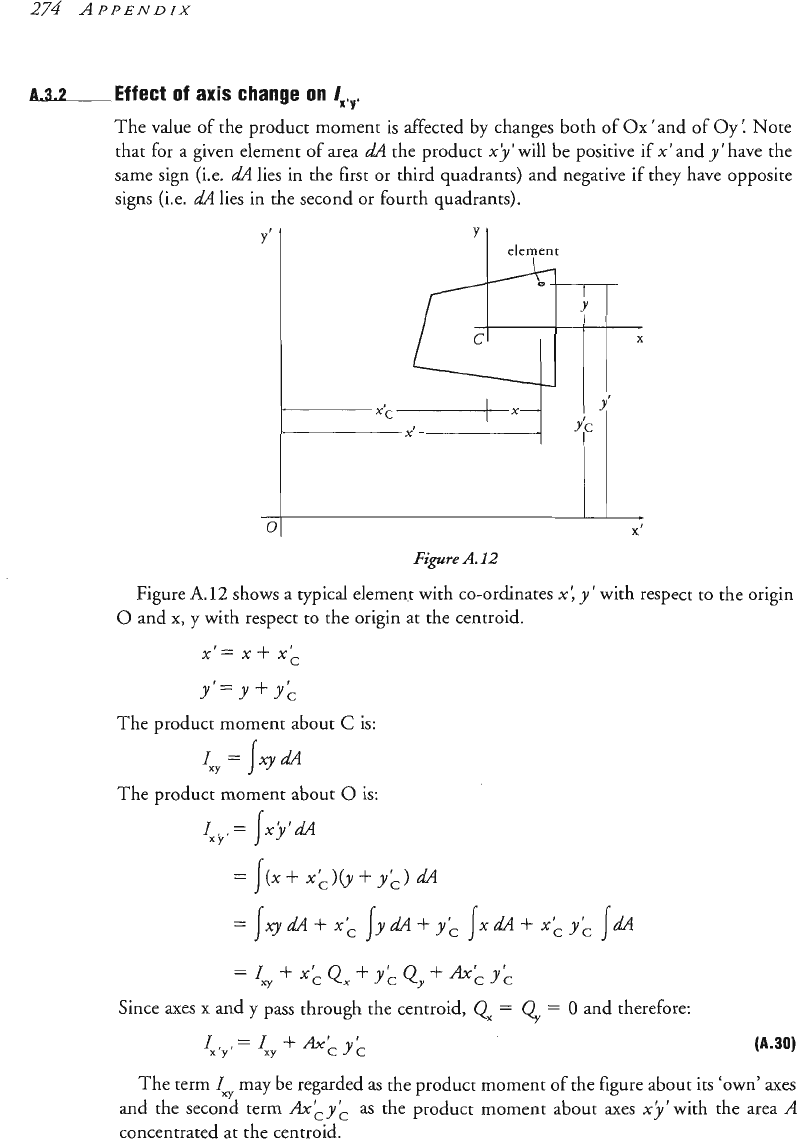
'Y'
The value of the product moment is affected by changes both of
Ox
'and of
Oy
Note
that for a given element of area
d4
the product xly'wiil be positive
if
x'and y'have the
same sign (i.e.
d4
lies in the first or third quadrants} and negative if they have opposite
signs (i.e.
d4
lies in the second or fourth quadrants).
Figure
A.
12
Figure
A.
12
shows a typical element with co-ordinates x;
y
'
with respect to the origin
0
and
x,
y
with respect to the origin at the centroid.
x'
=f:
x+ x;:
.Y'":Y+Y:,
The product moment about
C
is:
I-=
Ixyd
I&'=
~xlyld4
The product mo~ent about
0
is:
=
!(x+ x;:,(Y+y:,>
=I,'x;:Q,+Y;:QY+~;:y;:
Since axes
x
and
y
pass through the centroid,
Q
=
=
0
and therefore:
I&
=
I-
+
Ax:,
y;:
The term
Iw
may be regarded as the product moment of the figure about its 'own' axes
and the second term
Ax;
y
as
the product moment about axes xj
'
with the area
A
concentrated at the centroid.
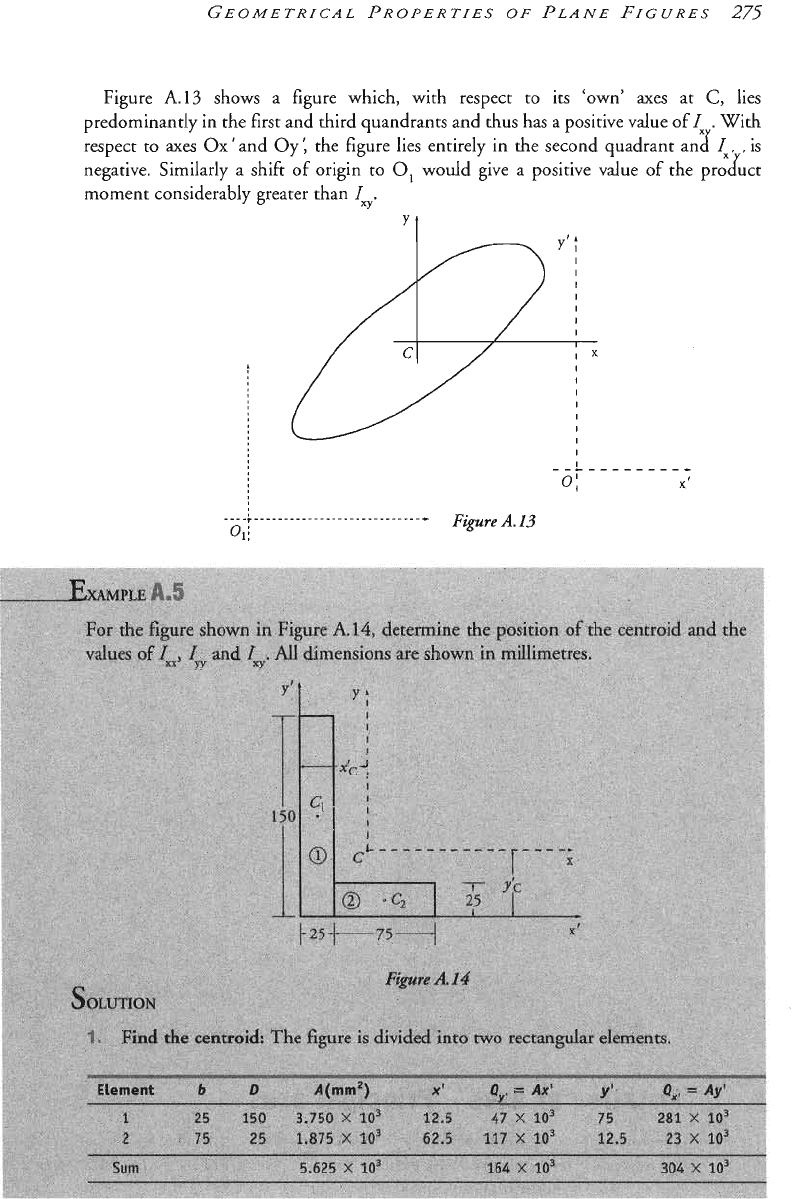
Figure
A13
shows a figure which, with respect to its 'own' axes at
C,
lies
predominantly in the first and third quandrants and thus has a positive value of
I
With
respect to axes
Ox
'
and Oy the figure lies entirely in the second quadrant an2
L,
,
is
negative. Similarly a shift of origin to
0,
would give a positive value
of
the proluct
moment considerably greater than
Ix,.
t
I
I
""""""
0:
X'
""t"""""""""""""""
01
i
Figwe
A.
13

Suppose that the figure shown in Figure
A.
14
(page
27’5)
is
subjected to
a
linearly varying
pressure with zero pressure along either
Cx
or
Cy.
There will be no resultant force but
there will be a moment about both
Cx
and Cy since
Ixy
is
not zero.
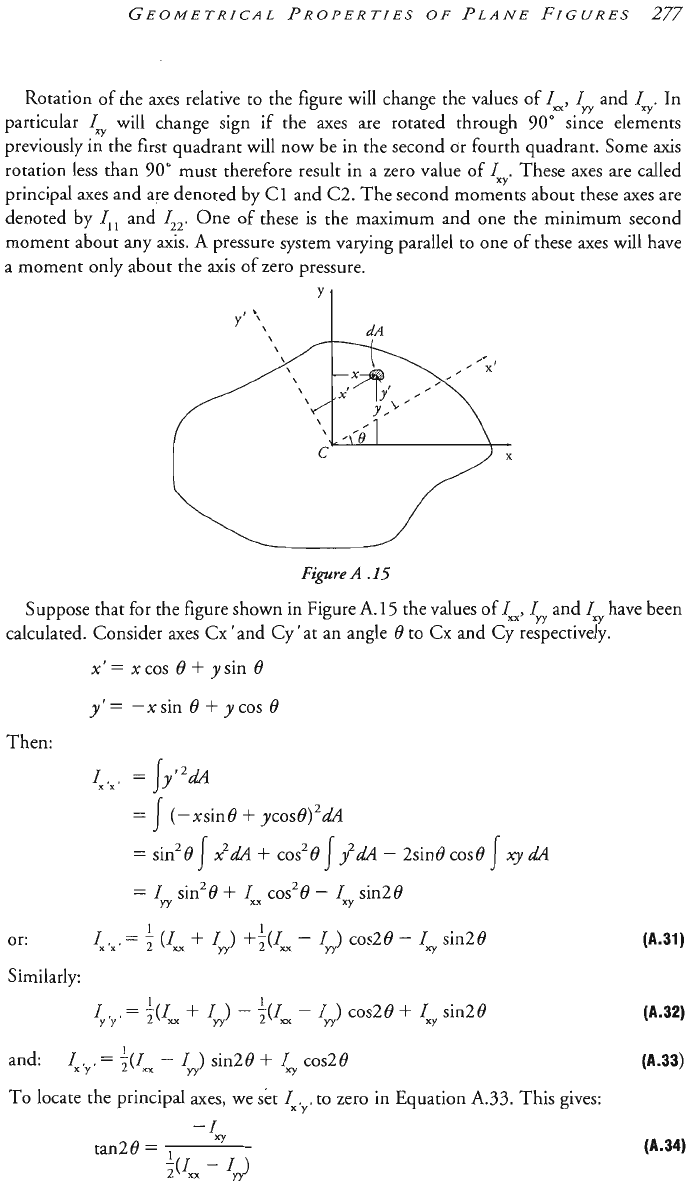
Rotation of the axes relative to the figure will change the values of
IXX,
Iyy
and
IXy.
In
particular
IXy
will change sign if the axes are rotated through
90"
since elements
previously in the first quadrant will now be in the second ar fourth quadrant, Some axis
rotation less than
90"
must therefore result in a zero value of
IT.
These axes are called
principal axes and are denoted by C1 and C2. The second moments about these axes are
denoted by
I,,
and
122.
One of these is the maximum and one the ~inimum second
moment about any axis.
A
pressure system varying parallel to one of these axes will have
a moment only about the axis
of
zero pressure.
'l
Suppose that for the figure shown in Figure
A.
15 the values
of
I=,
Iyy
and
IXy
have been
calculated. Consider axes Cx
'
and Cy
'
at an angle
8
to
Cx and Cy respectively.
X'=
xcos
8
+
ysin
8
yr
=
-xsin
8
+
y
cos
8
Then:
=
sin28
J"
+
cos28
J"
yd
-
2sin8 cos8
J"
qt
=
r'
sin2@
+
I~,
cos2@
-
I~
sin2
8
I'
(x
~
=
?
(I,
+
1')
+;(Im
-
I")
cos2
8
-
Ixy
sin2
8
or:
Similarly:
l
S
'y,y,
=
?(I=
+
I,,,
-
z(Im
-
IT)
cos28
+
Ixy
sin28
S S
and:
I
,
~
=
?(Ixx
-
IT)
sin28
+
IT
cos28
To locate the principal axes, we set
IXt,
to
zero in Equation
A.33.
This gives:
1
XY

which results in
two
values of
20
which differ by
1
80",
or
two
values of
0
which diflier
by
90".
For
the figure examined in Example
A.5
(page
275),
we have:
1-3906 X
lo3
0.5(12012
-
4199)
X
10
tan20
=
7
=
+
1.00
Hence
20
=
45"
and
0
=
22.5",
or
20
=
225"
and
0
=
112.5"
The values of
AI
and are obtained from Equations
A31
and
A.32:
h,
=
0.5(12012 t-4199)
X
lo3
+
0.5(12012
-
4199) X
lo3
cos
45
+
3906
X
lo3
sin
45
=
$105 X
lo3
+
2762 X
lo3
+
2762 X
lo3
=
13629 X
lo3
mm4

(a)
F'
=
8.66 kN;
F'
=
5.0
kN.
(b)
Fx
=
-20.0 kN;
F'
=
-34.64 kN,
(c)
F,
=
-3.54
kN;
Fy
=
"3.54
kN,
(a)
F,
=
109.8 kN;
F,
=
77.65
kN.
(b)
F,
=
269.0
W;
F'
=
219.6 kN.
(C)
F,
=
200.0
kN;
Fv
=
-
103.5
W.
P
=
73.21 N and
Q
=
51.76
N.
R
=
91.70
N
at
0
=
23.67".
R
=
62.5
N
at
8
=
39.84".
R
=
834.5 N at
8
=
7.32".
(a)
R
=
6.38
N
at
0
=
-
16.42".
(b)
R
=
3.427
N
at
8
=
-10.01".
(c)
R
=
97.90 N at
0
=
102.4".
R
=
8.04
kN
at
0
==
223.2".
(i) (a)
a
=
53.1" (or -53.1") and
A
=
20 N (or -20 N).
(b)
a
=
25.84" (or -25.84") and
A
=
19.11 (or 1.67
N).
(c)
a
=
100.3"
and
A
=
11.1 N or
a
=
199.7" and
A
=
-27.1 N.
(ii) (a)
a
=
126.9" (or
-
126.9") and
A
=
20
N
(or -20 N),
(b)
a
=
154.2" (or -154.2") and
A
=
-1.67 N (or -19.10
N).
(c)
a=
19.7" and
A=
"27.1
N
or
a
=
-79.7" and
A
=
-11.1
N.
0
=
41.54" and
P
=
283.4 N.
FA,
=
1795
N
and
FBc
=
2199 N.
R
=
95.39 N at 53.01";
FUR
=
98.62 N and
FvR
=
30.53
N.
0
=
146.0".
a
=
69.92" and
p
=
9.39".
R
=
26.90 kN and
P
=
27.90 kN.
P
=
6.66 kN and
a
=
121.7".
Q
=
-15.63
N
and
P
=
-24.92
N.
F',
=
-120.2 N and
FBc
=
833.3 N.
169.4." and 253.1" respectively, or 219.8" and 136.1" respectively.
H=
10.56
N
RA
=
10.29 kN at 48.33" to the horizontal and
&
=
11.1
1
kN (upwards).
Force in connecting rod,
F,,
=
1.02
kN
compression; Force
on
cylinder wall
=
0.20 kN.
(i)
RB
=
0.289K
(ii)
RA
=
0.764W at 10.9" to the vertical.
p
=
0.577.
F
=
19.36 N.
FA,
=
219.9
W
cornpression;
FAc
=
72.3 kN tension;
FDA
=
100 kN.
