Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.


x
If
any component is acted upon by only
two
forces, these forces must be equal and
opposite and in the same line. Suppose the bar
AB
(Figure 6.4a) has forces exerted on it
through the pins at
A
and
B
only. Then
F'
=
FB
and these act along the line
AB.
If
the
forces have been expressed in terms of components (Figure 6.5b), then not only is:
(<)A
=
(<)B
and
(Fy)A
(Fy
)B
as
we can see by taking moments about
B.
p/
If
a body
is
acted on by three forces only, these forces must be concurrent.
The laws of equilibrium may be applied to the complete structure and also to any
subsection of the structure. It cannot be too strongly emphasized that before any
equatio~s are written it
is
essenti to decide what p~ticular force system
is
under
co~si~eration,
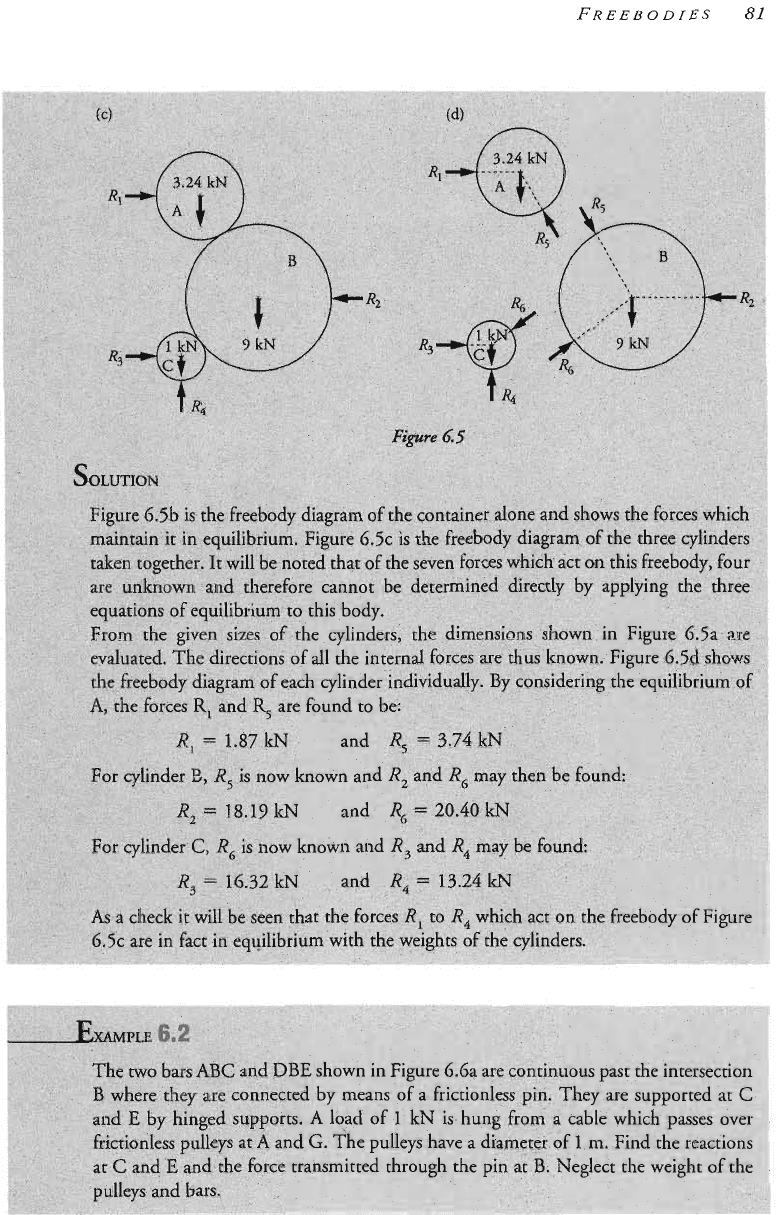

A
great many practical problems cannot be solved without considering the equili~rium
of components as we11
as
the equilibrium of the whole structure.
A
com~on
case
is
that
of a simple plane frame (Figure 6.7a) consisting of
two
rigid members
ABC
and
C
joined together by a frictionless hinge at
C
and supported at
A
and
E
by pin supports.
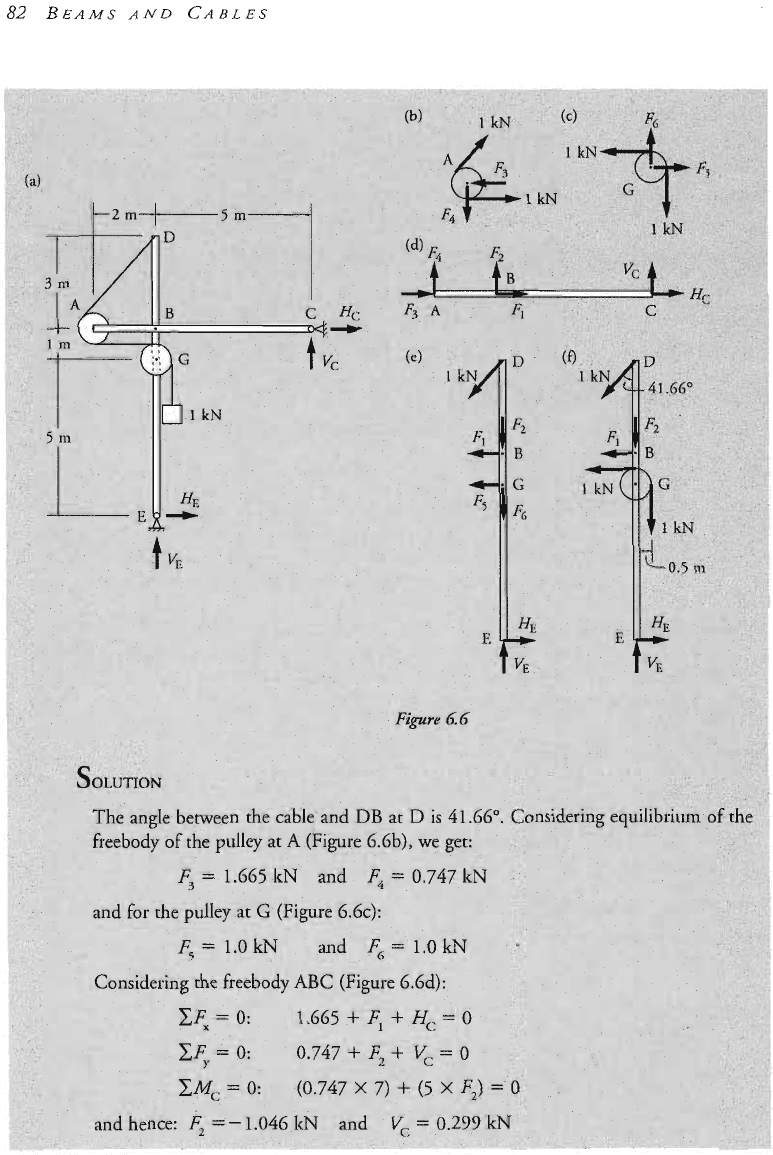
Reference to Figure 6.3a indicates that there are four reactions components altogether,
namely
HA
and
VA
at A and
H,
and
V,
at
E.
Since there are only three equations of
equilibrium for the frame
as
a whole, the external reactions cannot be evaluated without
considering freebodies of the components, Figure 6.7b shows freebody diagrams for each
of the Components ABC and
CDE
separately. We now have a total of six unknown force
components, but since there are three equilibrium equations for each component, the
problem is easily solved.
As
an alternative we could have drawn a freebody of the whole
frame and a freebody of one component. This particular type of problem will be
discussed in more detail in Chapter
8.
Many structures are built up of physically identifiable components. For instance the
ladder of Figure
6.1
comprises the part
AD
with the steps, the supporting leg DF and
the rope BE. A roof truss comprises a number of bars which are connected together at
their ends. In this chapter so far the impression may have been given that a freebody
should be separated from the complete structure at the junction between physical
components. In fact the components themselves may be subdivided.
A single beam may be arbitrarily divided into
two
parts and one part considered
as
a
freebody in order that we may find the force transmitted at the interface between the
two
parts. This particular problem is considered in Chapter
7.
For each of the structures shown in Figure
PG.
1,
draw freebody diagrams of
the complete system and of each of the components including the pins which
connect the various bars.

For each of the structures shown in Figure
P6.2,
draw a freebody diagram
for
each bar, each pin, the rope and the pulley.
For the pin-jointed truss of Figure
P6.3,
draw a freebody diagram for each bar
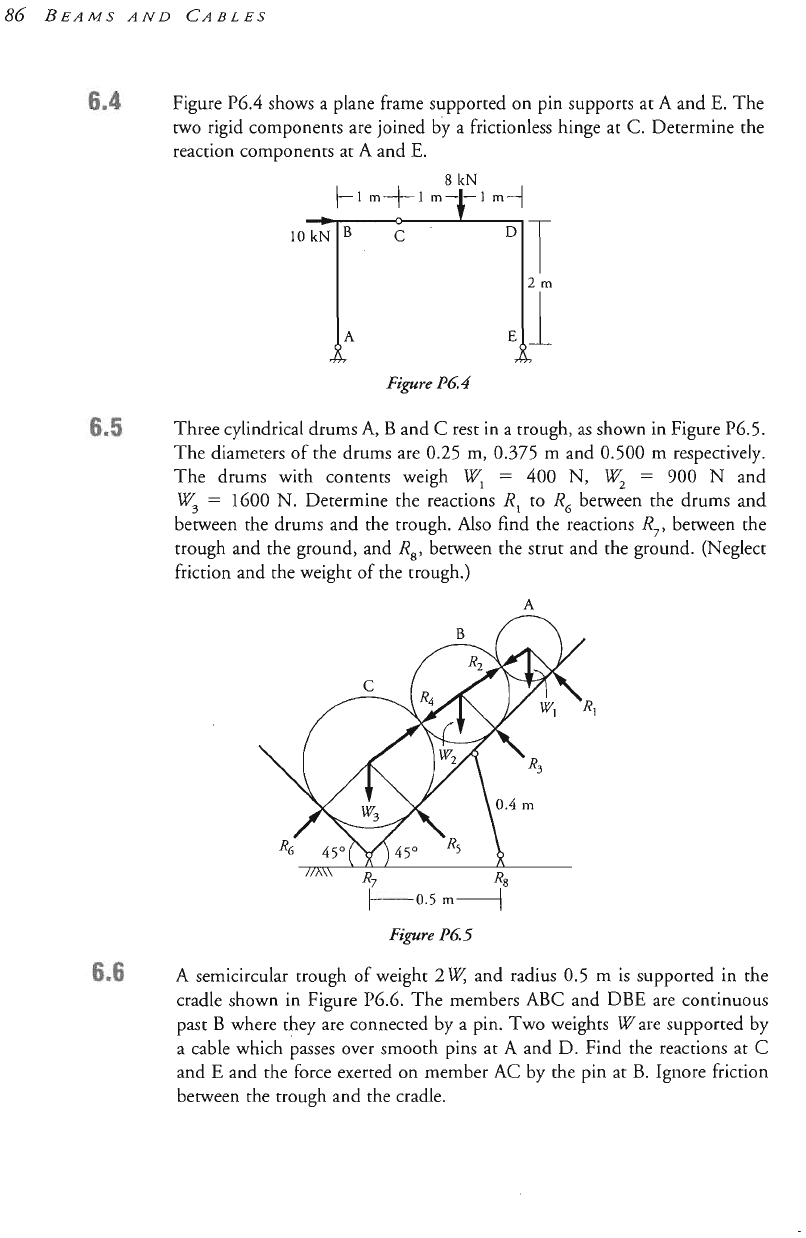
Figure
P6.4
shows a plane frame supported on pin supports at
A
and
E.
The
two rigid components are joined by a frictionless hinge at
C.
Determine the
reaction Components at
A
and
E.
Three cylindrical drums
A,
and
C
rest in a trough,
as
shown in Figure
P6.5.
The diameters of the drums are 0.25 m,
0.375
m
and 0.500 m respectively.
The drums with contents weigh
VI
=
400
N,
Wz
=
900 N and
W3
==
1600
N.
Determine the reactions
R,
to
R6
benveen the drums and
between the drums and the trough.
Also
find the reactions
R7,
between the
trough and the ground, and
R,,
benveen the strut and the ground. (Neglect
friction and the weight
of
the trough.)
A
A
semicircular trough of weight
2
W,
and radius
0.5
m
is supported in the
shown in Figure
P6.6.
The members
ABC
and
where they are connected
by
a pin. Two weight
a cable which passes over smooth pins at
A
and
D.
Find
and
E
and the force exerted on member
AC
by
the pin at
between the trough and the cradle.
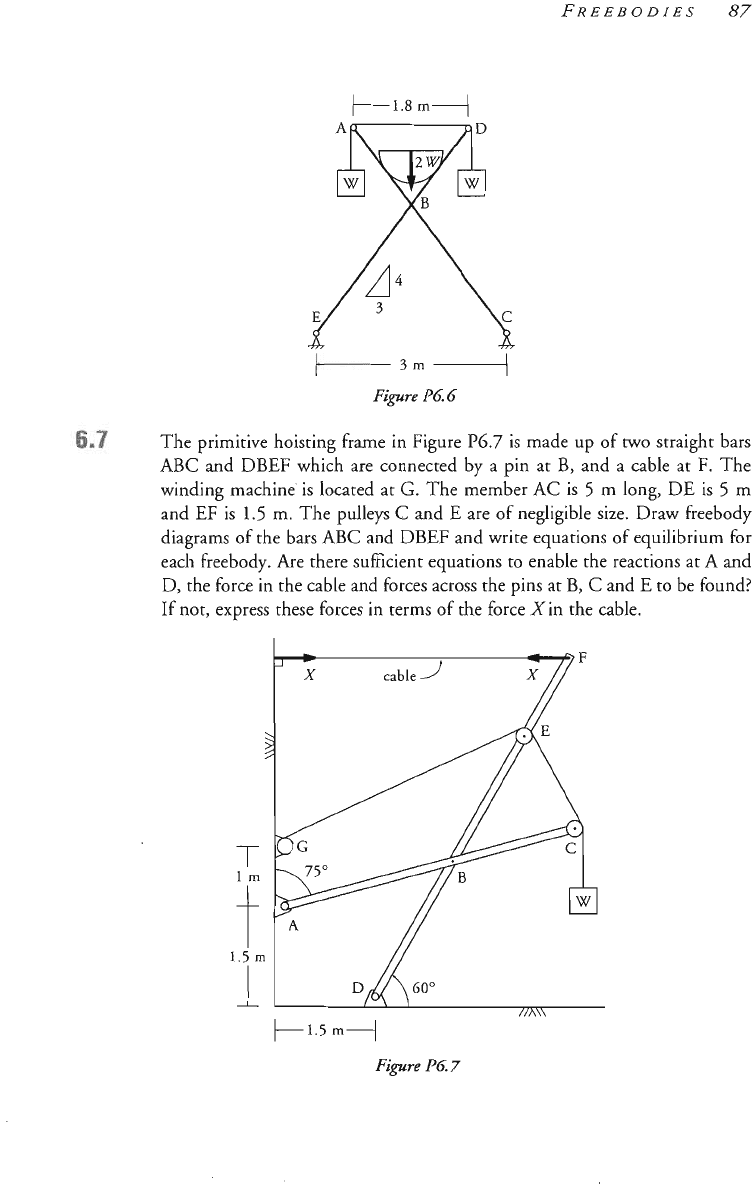
The primitive hoistin frame in Figure
P6.7
is
made up of
which are connected by a pin at
,
and a cable at
F,
The
is
located at
G.
The member
AC
is
5
m
i
.
The pulleys
G
and E are of ne~li~ible
siz
diagrams
of
the bars
ABC
and
DBEF
and write equations of equili~rium for
ch freebody. he there sufficient equations to enable the reactions at
A
and
,
the force in the cable and forces across the pins
at
B,
C
and E to be found?
If
not, express these forces in terms of the force Xin the cable.


ointed out in Chapter
G
that internal forces may
be
studied by ‘cuttin
a freebody diagram of one part. If the
n question is then an external force acti
freebody and it can be determined by statics.
his method
is
of importance when studying the forces and couples acti
beam by reason of externally applied loads. That such internal actions
e seen by consideri~~~ a beam AB in Figure
7.
l,
supported at each end and carryin
a
weight
K
In this condition, each part of the beam is at rest. Now if the beam
is
cut
through at a cross-section such as C, each part collapses (i.e. neither
AC
nor CB is
in
~~uilibrium). Some force must therefore have been tra~~smitted previously across the
secrion C
in
order to maintain equilibrium. The details of this force
the laws of statics either to the body AC or to the body
section
C
is an external surface of both of these bodies,
The present treatment will be confined to beams lying in one plane and subjected to
Consider the straight beam
ABCD
in e~uilibrium under the action of the forces
ure 7.2a. Suppose that it
is
required to determine the force transmitted
across the section C which
is
3
m
from
A.
The bar is cut through at C and the
equilibriu~~ of either AC or CD is examined. Figure 7.2b shows the freebody diagram of
the portion AC which is acted upon
by
the given forces at
A
and
B
and by an
unknown
force
Q.
Since AC
is
in equilibriu~, the unknown force Qmust be the equilibrant of the
other
WO
and is determined by the method of Section
5.1.
forces lying in the same plane.
