Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.

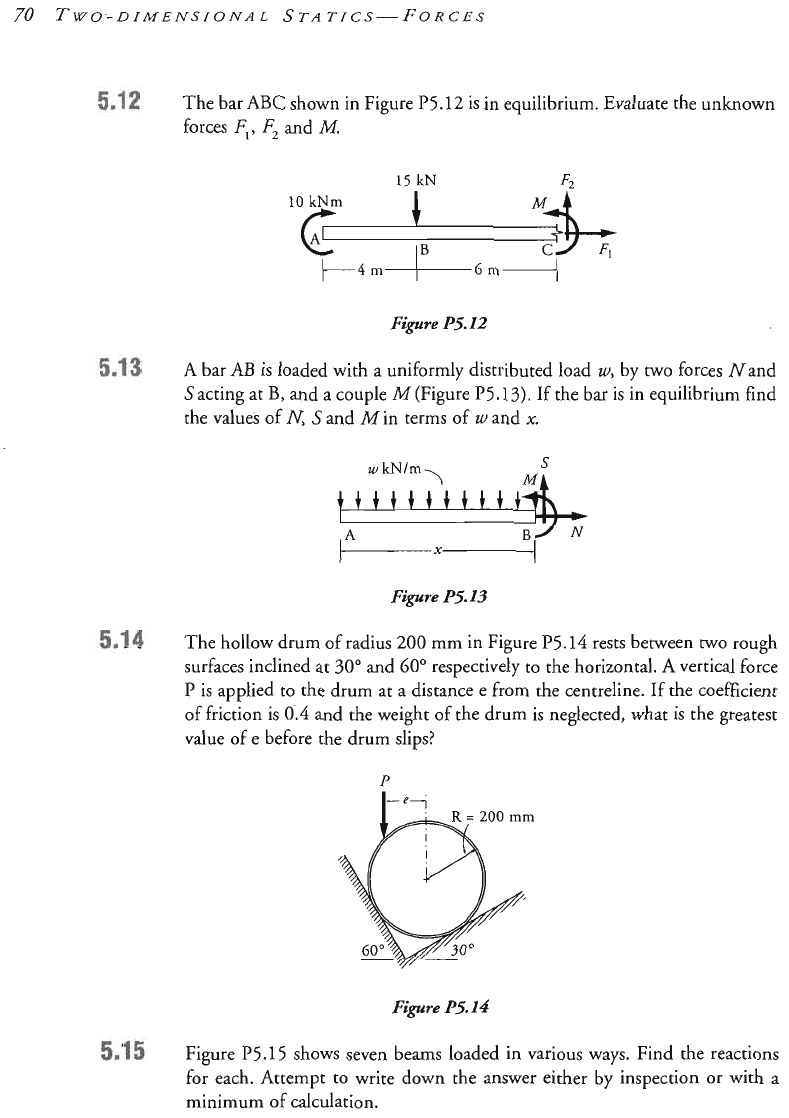
The bar
ABC
shown in Figure P5.12
is
in e~uilibrium. Evaluate the unknown
forces
F,,
Fz
and
M.
re
A
bar
AB
is
loaded with
a
uniformly distributed load
W,
by
two
forces Nand
S
acting at
B,
and a couple
M
(Figure PS.
13).
If the bar is in e~uilibrium find
the values
of
N,
S
and
M
in terms
of
W
and
x.
W
kNlm
-..
S
The hollow drum of radius
200
mm
in Figure P5.14 rests between
two
rough
surfaces inclined at
30"
and
60"
respectively to the horizontal.
A
vertical force
P
is applied to the drum at
a
distance e from the centreline. If the
coefficient
of friction is 0.4 and the weight of the drum is neglected, what
is
the greatest
value of e before the drum slips?
P
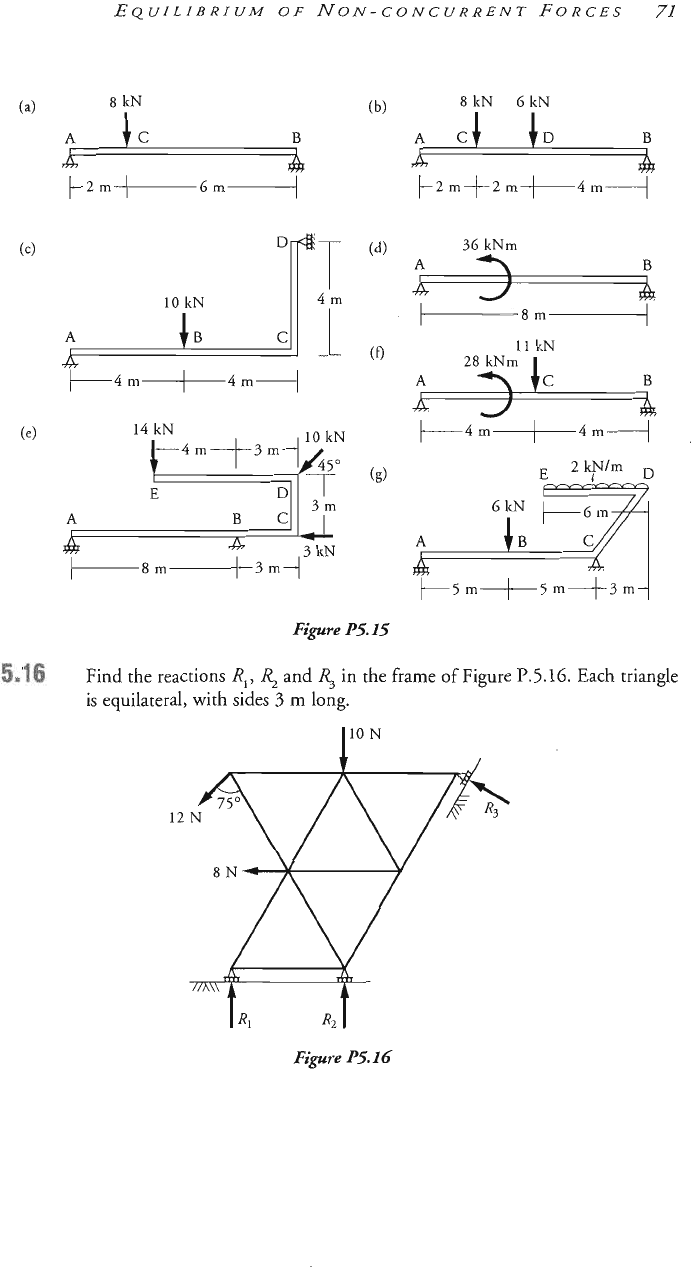
Figure
P5.15
shows seven beams loaded in various
ways.
Find the reactions
for each. Attempt to write down the answer either by inspection
or
with
a
~inimum of calculation.
EQurLrerrrun/r
OF
NON-CONCURRENT
FORCES
71
A
B
14
kN
re
36
kNm
11
kN
28
kNm
Find the reactions
RI,
R,
and
R3
in the frame
of
Figure
P.5.16.
Each
triangle
is e~uilater~, with sides
3
m
long.
10
N
12
re
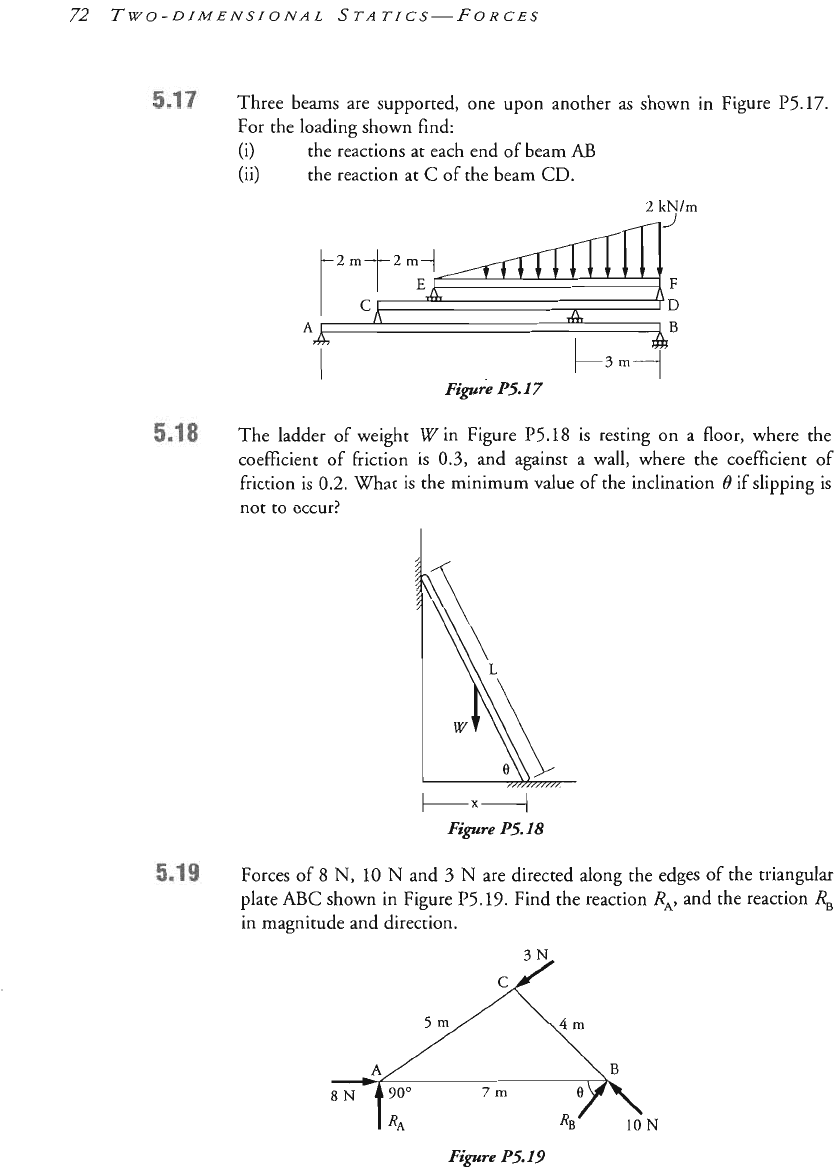
Three beams are supported, one upon another as shown in Figure P5.17.
For the loading shown find:
(i) the reactions at each end of beam AB
(ii) the reaction at
C
of the beam
CD.
2
kNltn
The ladder
of
weight
W
in Figure P5.18 is resting on a floor, where the
coeflicient of friction is
0.3,
and against a wall, where the coefficient of
friction is
0.2.
What
is
the minimum value of the inclination
8
if slipping is
not to occur?
Forces of
8
N,
10
N
and
3
N
are directed along the edges
of
the triangular
plate ABC shown in Figure PS. 19. Find the reaction
RA,
and the reaction
4
in magnitude and direction.
N
EQUILIBRIUM
OF
NON-CONCURRENT FORCES
73
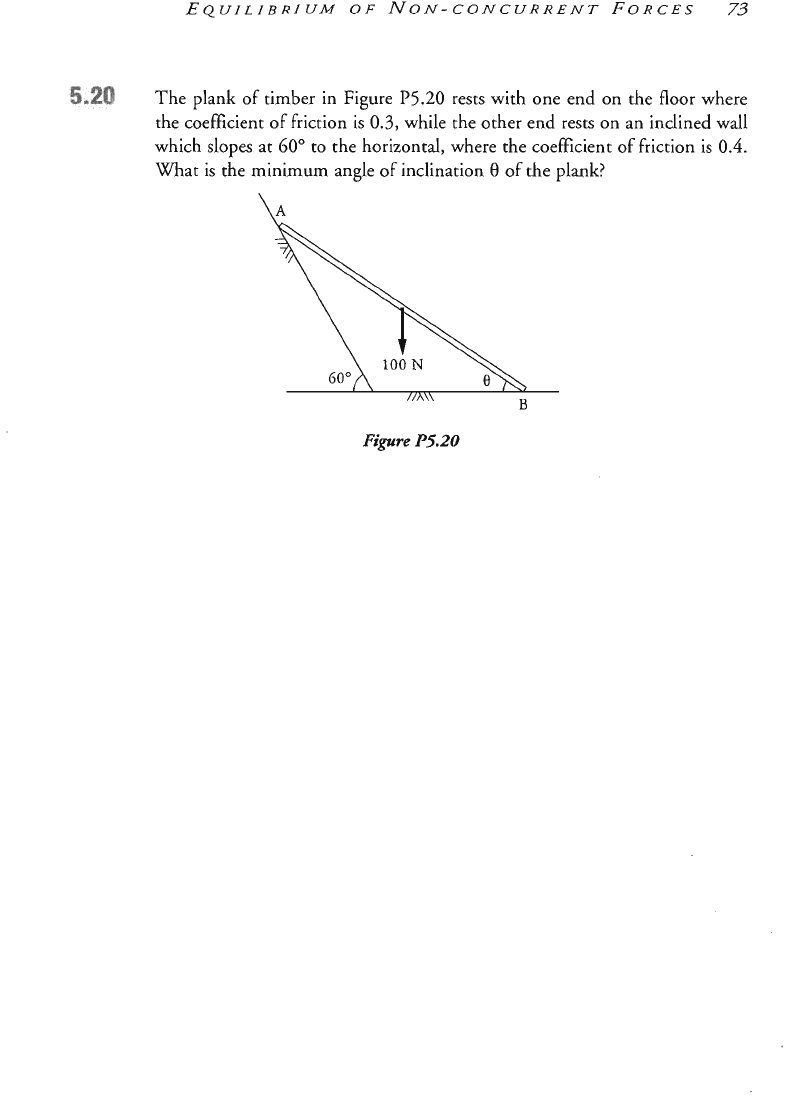
The plank of timber in Figure
P5.20
rests with one end on the floor where
the coefficient of friction
is
0.3,
while the other end rests on an inclined wall
which slopes at
60"
to the horizontal, where the coefficient of friction
is
0.4.
mat is the ~ini~u~ angle
of
inclination
0
of the plank?
\A




In Part
1,
the equations of equilibri~m were employed to express relationships between
the external forces acting upon a single body
or
structure, In this way, if some of the
external forces were known, other forces, usually reactions at supports, could be
eral, much more infor~ation
is
required about a structure than
Most structures and machines are built up of several components connected together.
Such components exert forces upon one another at their junctions, and it
is
necessary to
evaluate these forces. Such forces are
~~~~~~Z
to the structure
as
a whole, and no
information can be obtained about them by considering the equilibrium of the complete
structure. ~ccor~ing to Newton’s Third Law, the force exerted by component
X
upon
connponent
U
is
equal and opposite to that exerted by
Y
upon
X.
So
even if we attempt
to include these forces in the e~uilibrium equations they will cancel out.
The only way we can obtain infor~ation about such forces is
to
consider the
t
of the structure. The part is
so
chosen that the internal force in
alto that part. The notion of the
~ee~~~~
is of inn
ters we introduced the concept of the freebody a
can be este~d~d to apply to a
RF
RA
Fipre
6.1
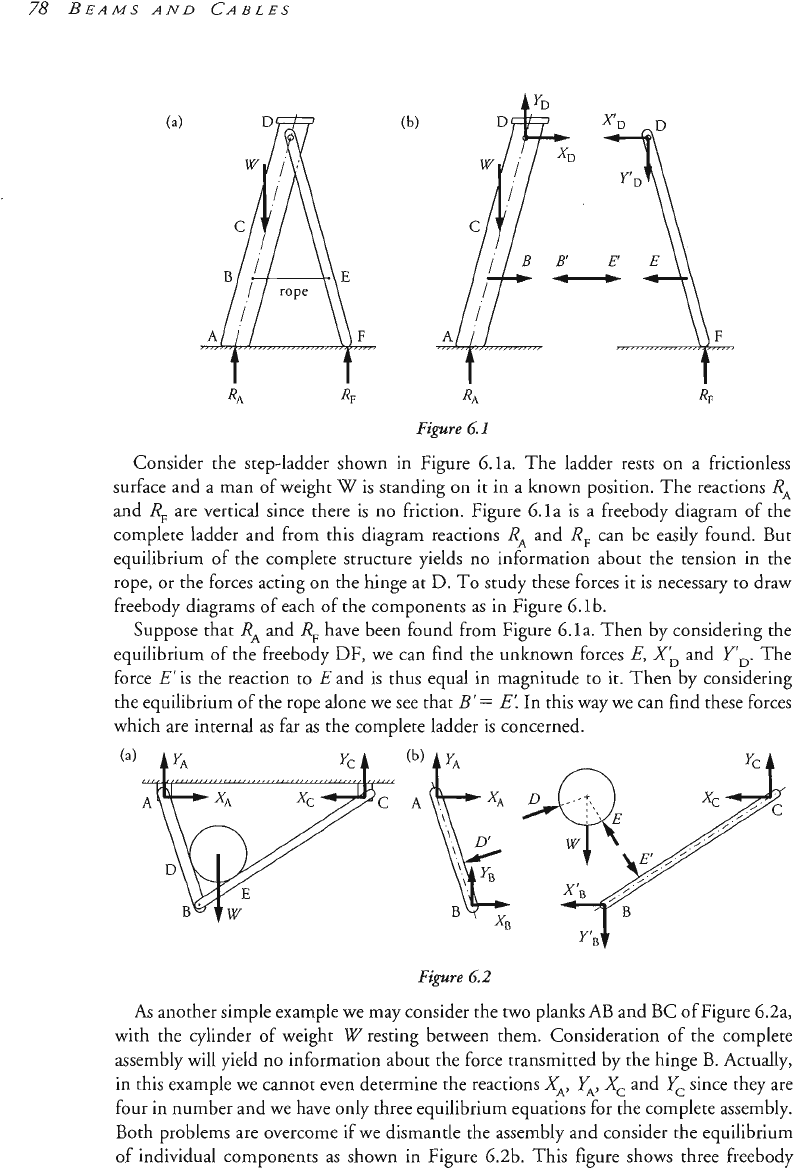
Consider the step-ladder shown in Figure
6.
la. The ladder rests on a frictionless
surface and a man of weight
W
is standing on it in a known position. The reactions
RA
and
RF
are vertical since there is
no
friction. Figure
6.
la
is
a freebody diagram of the
complete ladder and from this diagram reactions
RA
and
R,
can be easily found.
equilibrium of the complete structure yields no information about the tension in
rope, or the forces acting on the hinge at
D.
To study these forces it is necessary to draw
uppose that
RA
and
I-$
have been found from Figure &la. Then by considering the
equilibrium of the freebody DF, we can find the unknown forces
E,
X;,
and
YD.
The
force
E’
is
the reaction to
E
and
is
thus equal in magnitu~e to it, Then by considering
the equilibrium of the rope alone we see that
B’=
E:
In this way we can find these forces
which are internal as far as the complete ladder
is
concerned.
ody diagrams of each of the components as in Figure 6.1 b.
As
another simple example we may c e
two
planks AB and BC of Figure 6,2a,
with the cyiinder of weight
V
resting between them. Consideration of the complete
assembly will yield no information about the force transmitted by the hinge
B.
Actually,
in this example we cannot even determine the reactions
XA,
YA,
Xc
and
Yc
since they are
‘n number and we have only three e~uilibrium equations for the complete assembly.
problems are overcome
if
we dismantle the assembly and consider the equili~rium
of individual components as shown in Figure 6.2b. This figure shows three freebody
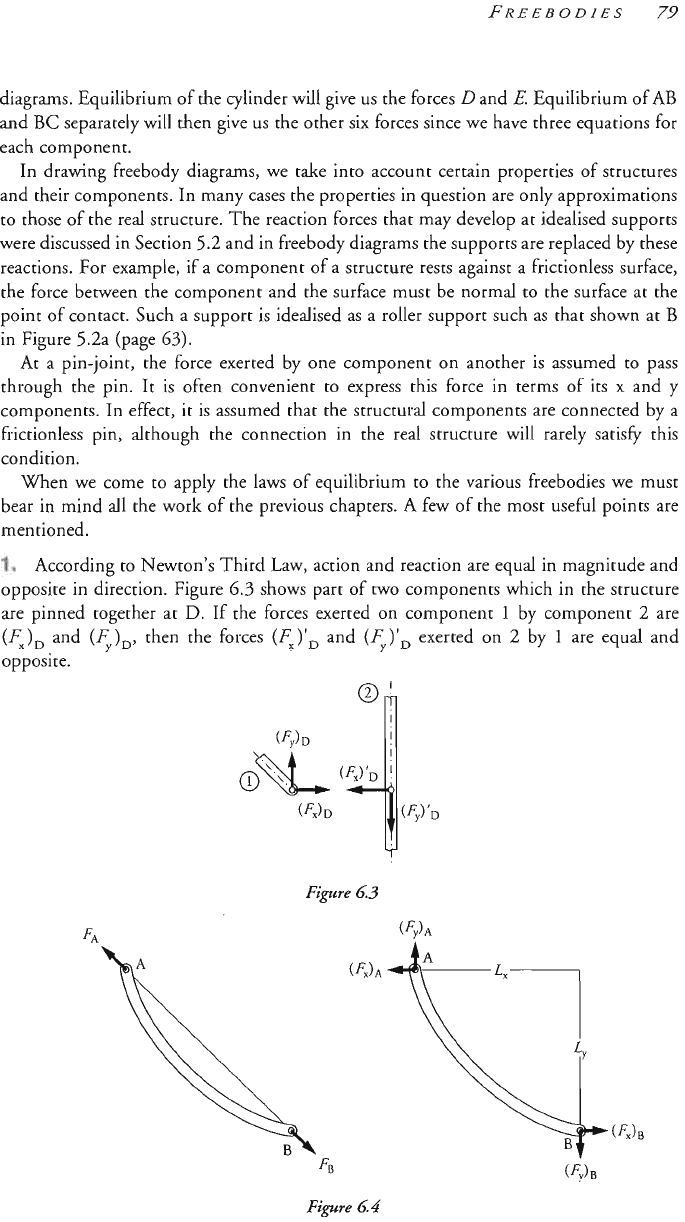
diagrams. Equilibrium of the cylinder will give
us
the forces
D
and
E
Equilibrium of AB
C
separately will then give
us
the other six forces since we have three equations for
In drawing freebody diagrams, we take into account certain properties of structures
and their components. In many cases the properties in question are only approximations
to those of the real structure. The reaction forces that may develop at idealised supports
were discussed in Section
5.2
and in freebody diagrams the supports are replaced by these
reactions. For example, if a component of a structure rests against a frictionless surface,
the force between the component and the surface must be normal to the surface at the
of contact. Such a support is idealised as a roller support such as that shown at B
ure 5.2a (page
63).
At
a pin-joint, the force exerted by one component on another is assumed to pass
through the pin. It
is
often convenient to express this force in terms of its
x
and y
components. In effect, it is assumed that the structural components are connected by a
frictionless pin, although the connection in the real structure will rarely satisfj. this
condition.
men we come to apply the laws of e~uilibrium to the various freebodies we must
bear in mind all the work of the previous chapters. A few of the most useful points are
mentioned.
According to Newton's Third Law, action and reaction are equal in ma
opposite in direction. Figure
6.3
shows part of
two
components which in the structure
are pinned together at
D.
If the forces exerted on component
1
by component
2
are
(c),
and
(Fy)L,,
then the forces
(Fx)',
and
(FY)lD
exerted on
2
by
1
are equal and
opposite.
