Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.


uch of the work of statics consists of replacing a given system of forces by a statically
quivalent system which is more convenient for calculating the effect of the system.
~o-dimen~iona~ system of forces can be replaced by any other system in
which there are at least three independent quantities, If there are just three unkno~n
quantities in the new system, these quantities may be specifically deter
the new force system is equivalent to the original force system.
If
the new force system
contains more than three unknown quantities, a certain amount
of
choice exists in
consider here only the case of three unknown quantities. These three unknowns
a system of forces by its resultant is one such example.
ing magnitudes to these unknowns.
must then be chosen
so
that the new system and the given system are:
as regards their
x
components
as re ards their y components
ards their moments about any chosen point.
X

NON-CONCURRENT FORCES
51
Suppose that the given system consists of the single force
F;
acting at
A
(xl,
y,)
in a
direction
B,
to the
x
axis (Figure
4.18a).
Suppose it is required to replace it by an
equivalent system consisting of a force
XI
along the x axis, a force
Y,
along the y axis and
a couple
MI
(Figure
4.18b).
Equating the
x
and y components of the new system to the
x
and y component of the given system, respectively, gives:
XI
=
Fl
cos
6',
and
Y,
=
Fl
sin
4
Moments can be equated about any point, but the origin
is
most convenient in this
particular problem:
MI
=
Fl
xI
sin
Bl
--Fl
y1
cos
6',
In a similar
way,
we
could replace a system consisting of any number of forces
Fl,
F2
etc. acting in directions
B,,
%
e&. by a new system comprising forces
X
and
along
the x and y axes, and
a
couple
M.
By equating the new system to the given system
as
above, we obtain:
Of
course, it is not necessary for the three components of the new system to act at the
origin. They can be specified to act anywhere,
as
in Example
4.7.

The new system need not consist of forces
X
and
Y
together with
a
couple, For
instance, when
a
force system is replaced by its resultant, the new system (the resultant)
is
a
single force, the three unknown quantities being its magnitude, direction and
position. We could replace
a
given force system by three forces acting along the sides of
a specified triangle (although not proportional to the sides). in such
a
case the direction
and position of the new forces are known, and the unknown quantities are the three force
magnitudes. We could not replace
a
given system by three forces all parallel to the x axis
because such an arrangement would not permit the new system to provide
a
y
component equivalent to that of the original system. In effect, three parallel forces do not
represent three
~~de~e~de~t
quantities.
A
common example of the use of an equivalent system is the replacement of a force
by
a
parallel force and
a
couple, The force Fat in Figure
4.20
can be replaced by an
equal force
F
at
A
together with
a
couple of moment
Fd
The couple
Fd
has the same
moment about
A,
and is in the same sense,
as
the original force Fat
Q.
F
*
Suppose we have
a
force system expressed in the form
of
three components
XA,
YA
and
MA
in the axes at
A
(Figure
4.21).
We now decide that i auld be more convenient to
express the system in terms of components in the axes at shown, If the
WO
systems
are e~uivalent, then:

NON-CONCURRENT
FORCES
53
resolving parallel to
XB
gives:
XB
=
XA
cos
8
+
C
sin
t)
resolving parallel to
YB
gives:
UB
=
-XA
sin
8
+
cos
8
D
taking moments about B gives:
MB
=
X,y
-
+
MA
Figure
P4.
l
shows a lever pivoted at
R.
At a certain instant it is horizontal and
has forces shown exerted at the ends. The force exerted on the lever by the
pivot B
is
shown
in
terms of its horizontal and vertical ~omponents.
(i)
Find the moment of the force system about B.
(ii) Find the mo~ent
of
the force system about
C.
(ii) Which way will the bar rotate?
10
N
10
N
27.32
N
Figure
P42
shows three forces actin. on a bar ABC. Find the resultant.
80 N
80
N
c
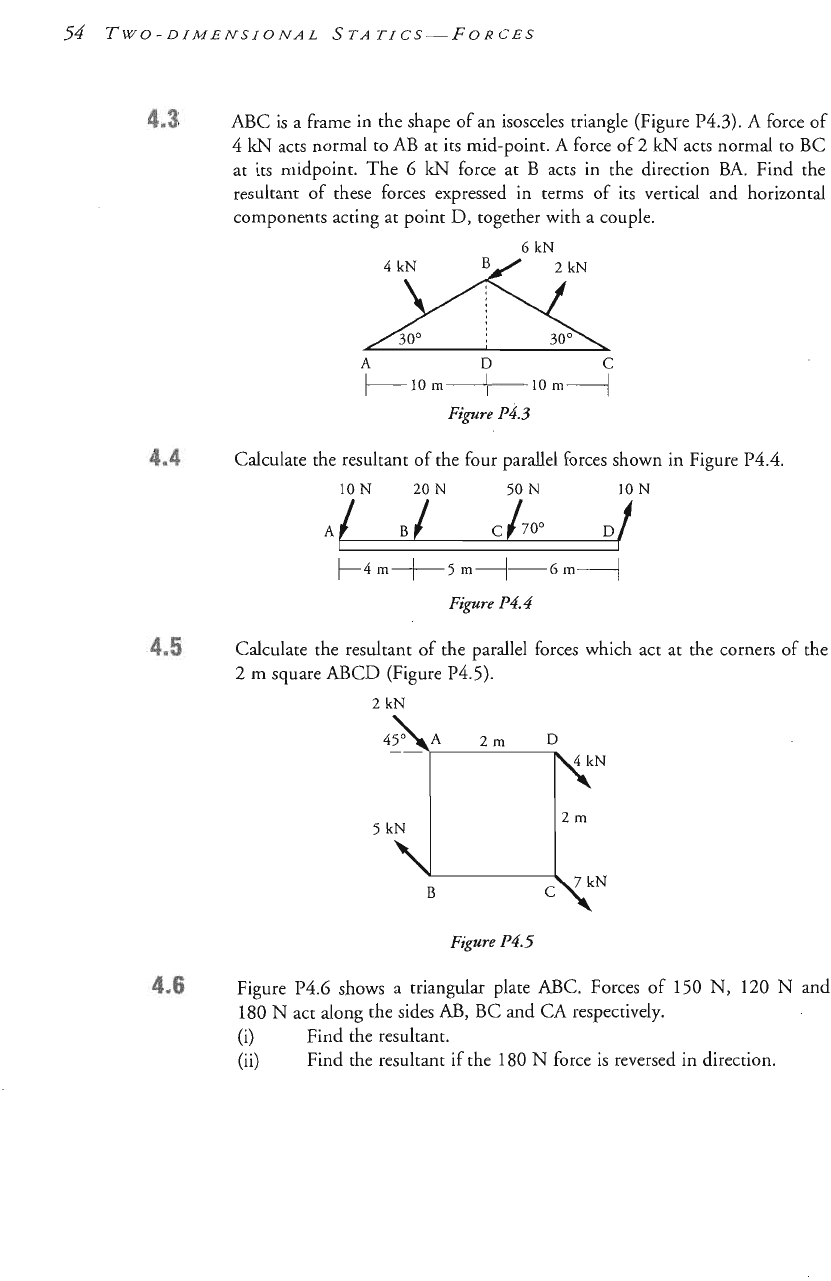
ABC is a frame in the shape of an isosceles trian e (Figure
P4.3).
A
force of
4
kN
acts normal to
AB
at its mid-point. A force of
2
kN
acts normal to
BC
at its midpoint. The
6
IsN
force at
B
acts in the direction
BA.
Find the
resultant of these forces expressed in terms of its vertical and horizontal
components acting at point D, together with a couple,
6
kN
Calculate the resultant of the four parallel forces shown in Figure
P4.4.
10N
20N
50
N
10
N
A
Calculate the resultant of the parallel forces which act at the corners of the
2
m square ARCD (Figure
P4.5).
2
kN
Figure
P4.6
shows a triangular plate ABC, Forces of
150
N,
120
N
and
180
N
act along the sides AB,
BC
and CA respectively.
6)
Find the resultant,
(ii) Find the resultant if the
180
N
force is reversed in direction.

NON-CONCURRENT
FORCES
55
120
A
rigid body
Al3CD
is loaded
as
shown in Figure
P4.7.
(9 Express the resultant of these forces
as
a
horizontal and vertical
(ii) Find
a
point
P
such that the resultant can be expressed
as a
horizontal and vertical component only, acting rhrough
P.
Figure
P4.8
shows a
1
m square plate
ABCD
acted upon by a force of
10
Id4
along the diagonal
BD
and
an
anticlockwise couple of
20
kNm at corner
A.
(i) Find the ~agnitude, direction and point of application of the
(ii) Solve the same problem but with the couple applied at
resultant force.
of
A.
m

Find the resultant of the five forces shown in Figure
P4.9.
D
3kN
In the parallelogram of Figure
P4
10,
sides
AB
and
DC
are
740
mm
while
sides
AD
and
BC
are
500
mm.
The forces shown act along, but are not
proportional to, the four sides of the parallelogram.
(i) Find
a
statically equivalent force system which consists of
a
force
(ii) Find
a
statically equivalent system which consists
of
a
single force.
through
A
and
a
couple.
Figure
P4
l
1
shows
a
square plate acted upon by forces of
8
lN,
12
kN
and
15
kN
and
also
a
couple of
20
INm.
These are shown by full lines.
&%at
forces (shown dashed) acting along the sides of the square will be statically
equivalent to the
original
system, given that
FI
=
c3
?
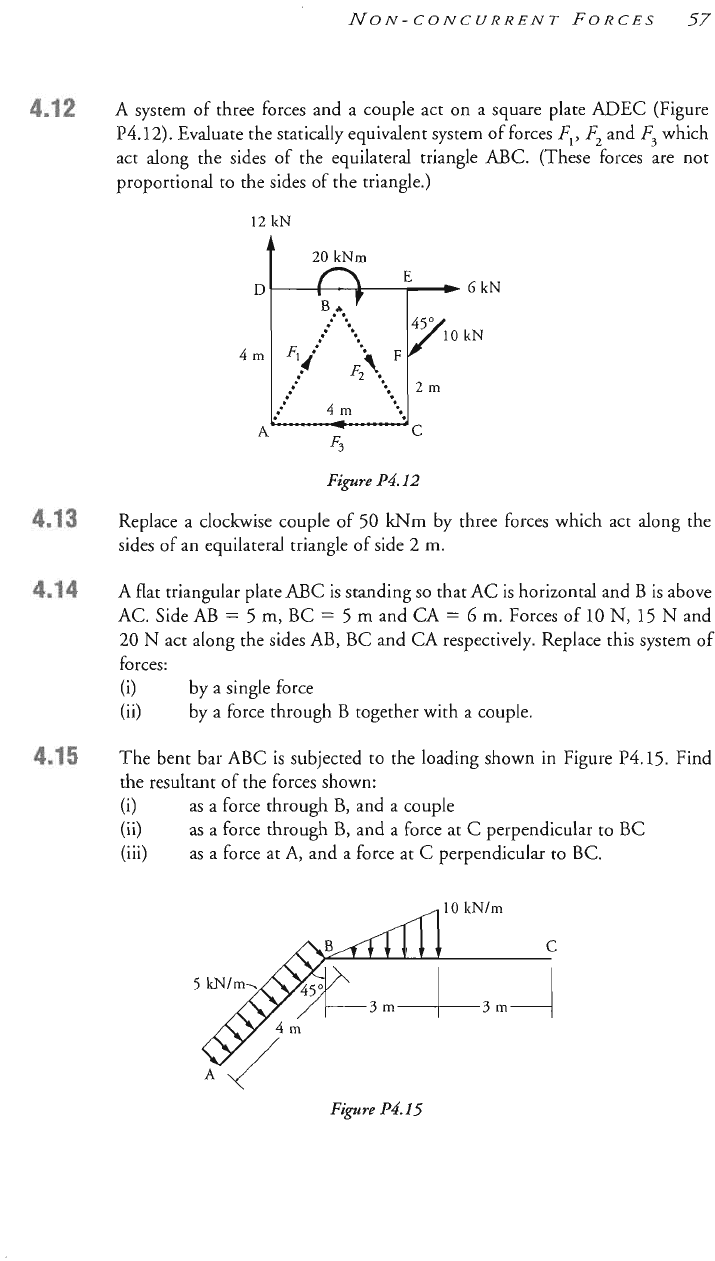
A
system of three forces and
a
couple act on
a
square plate ADEC (Figure
P4.12).
Eval~ate the statica~~y e~uiv~ent system
of
forces
PI,
F2
an
act along the sides
of
the equilateral triangle ABC, (These forces are not
proportional to the sides of the triangle.)
12
kN
6
kN
kN
~~~~~
Pd.
12
se couple of
50
kNm
by three forces which act dong the
sides of an equilateral triangle of side
2
m.
A
flat triangular plate ABC is standing
so
that AC is horizontal and
AC. Side AB
=
5
m,
BC
=
5
m and CA
=
6
m,
Forces
of
10
N,
20
N
act along the sides AB, C and CA respectively. Replace this system of
forces:
(ii)
by
a
force through
B
together with a couple.
(8
by a single force
The bent bar ABC is subjected to the loading shown in Figure
P4.
l
the resultant
of
the forces shown:
(i)
as
a force through
B,
and
a
couple
(ii)
as
a
force th~ough B, and
a
force at
C
perpendic~lar
to
(iii)
as
a force at A, and
a
force at C perpendicular to
BC.

Four coplanar forces act at the points A,
B,
C
and
D
as
shown in
Figure
P4.16.
The co-ordinates of each point are shown in brackets.
(i)
.
Find the resultant of the forces.
(ii) Replace the resultant by the
two
forces indicated by the dashed lines
in Figure
P4.16.
'l
10
N
B
("4,
3
c
(-3,
-3)
A system of coplanar forces acts
as
shown in Figure
P4.
17
along the lines
AB and BC. Replace the forces by an equivalent force through
D,
and a
couple at
C.
2
kNtm
f
I
1.5
m
2.5
m
D
J
"I
A system of coplanar forces, shown by solid lines, acts
as
indicated in Figure
P4.18.
Find the resultant
of
the system, expressed
as:
(i) a force through point
C,
and a couple
(ii) a force of
60
N
at
E,
and a force F appropriate~y directed and
located.
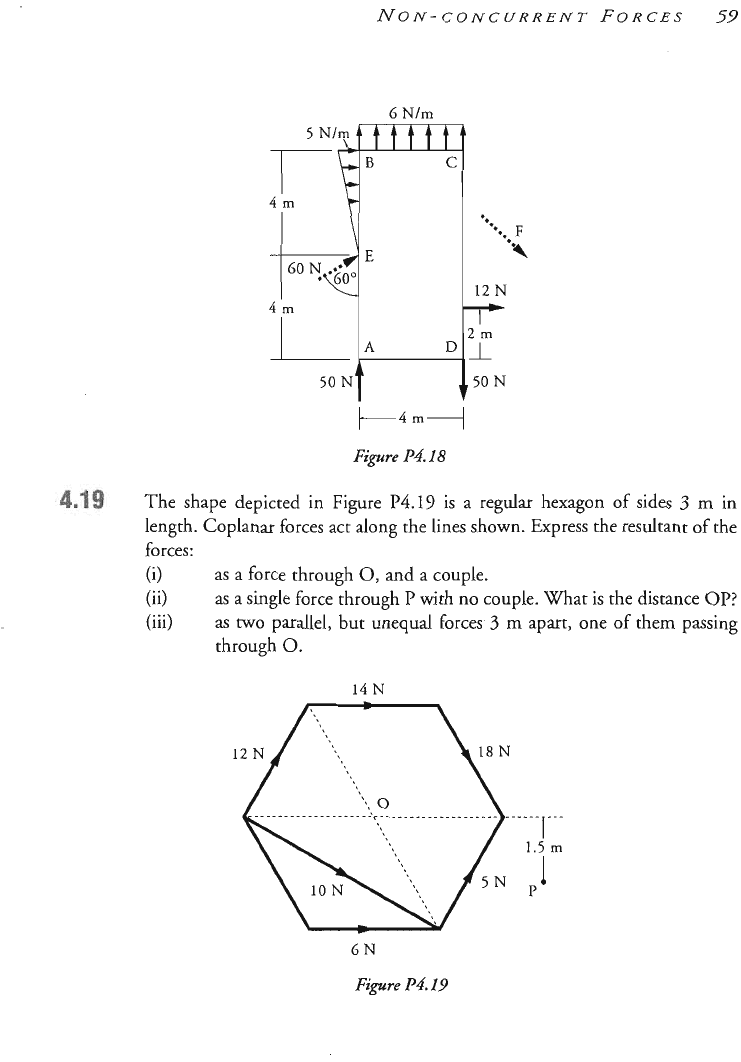
NON-CONCURRENT
FORCES
59
6
Nlm
m
apart,
one
of
them
passin
14
N
"-1"-
1.5
m
P
