Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.


the cut may well support only part of the distributed load and this part must be included
in.
the freebody diagram. After the cut has been made and the freebody drawn, the
part
ofrhe ~istributed load acting on the freebody
is
then replaced by
its
resultant.


The internal actions vary from point to point along a bearss. In simple cases it is possible
to express this variation in algebraic terms,
If
the bending moment is computed for
a
at
a
distance of
x
metres from a chosen origin (usually the left-hand end),
is obtained for Min terms of
x.
Similar functions may be derived for the
axial force and shear force. Usually such expressions are valid only over a limited part of
the beam. This is the case if the loading is discontinuous (i.e.
if
it consists of concentrated
loads, or of distributed loads over some parts only).
It
is
frequently convenient to illustrate the variation of bending ~oment by plotting
a graph of
M
against distance along the beam. Such a (often called a
~e~~~~~
~o~e~t
~~~~~~)
may be obtained either by plotting the aic hnctions mentioned
above, or by simply calculating
M
at
a
number of isolated points don
plotting these values
as
ordinates.



It can be seen in Example
7.8
that over the part of the beam which carries uniformly
distributed load the shear force varies linearly and the bending moment varies
parabolically. Over the unloaded part of the beam,
S
is
constant and Mvaries linearly,
This is discussed again in the next section.
t
beam loaded normal to its axis, simple relationships exist between the load
shear force and the bending moment. These relationships can be developed
from the equilibrium equations of a
small
element of the beam. It
is
assumed that the
beam
carries
distribute^
load, the intensi~ of which varies from point to point. The
~0~~
denoted by
W,
is the load per unit length of a beam at the particular section
considered. The upward direction
is
taken as positive for all quantities.
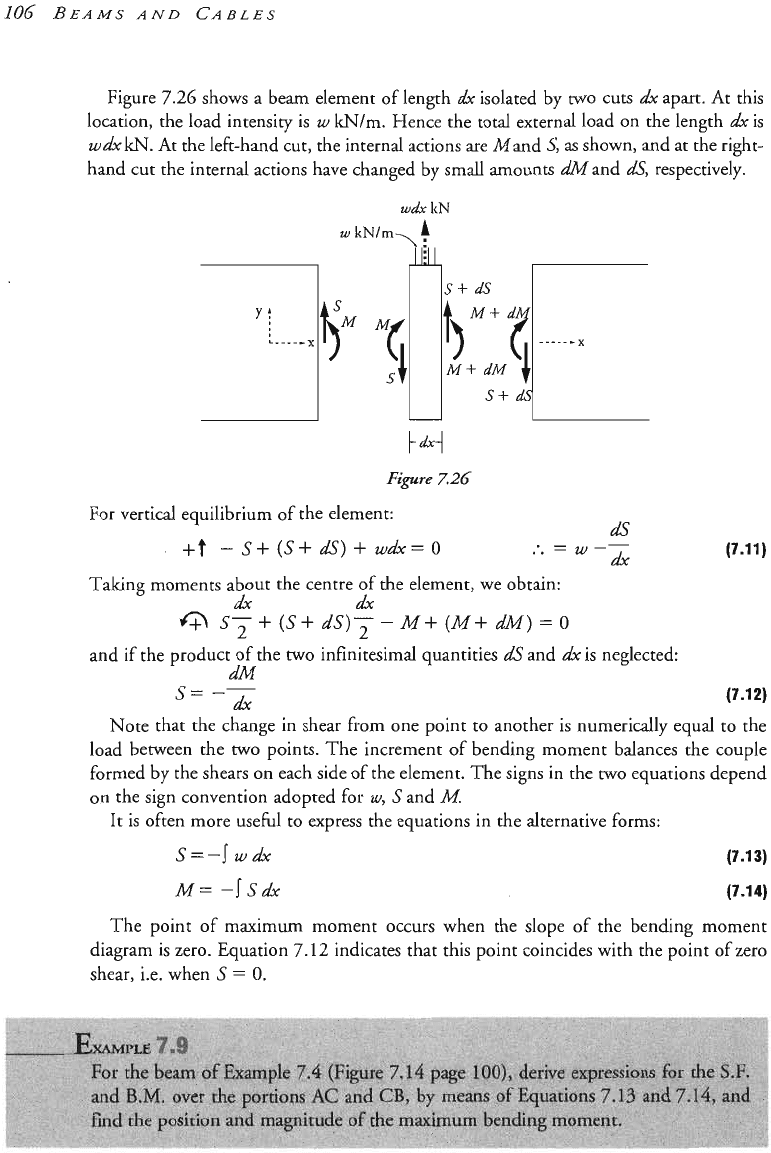
Figure
7.26
shows a beam element of length
dx
isolated by
two
cuts
dx
apart. At this
location, the load intensity is
W
kN/m. Hence the total external load on the length
dx
is
wdxkN.
At the left-hand cut, the internal actions are Mand
S,
as
shown, and at the right-
hand cut the internal actions have changed by small ~ounts dMand
&,
respectively.
wdx
kN
M+
""_)
+
dM
(~"11)
For vertical equilibrium of the element:
dS
-
S+
(S+
&)
+
wdx=O
Taking moments about the centre
of
the element, we obtain:
.-
**
-
w-z
dx dx
ST
+
(S+
dS)z
-
M+
(M+
dM)
=
0
and if the product of the
two
infinitesimal quantities
dS
and
dx
is neglected:
dM
S=
-
Note that the change in shear from one point to another is numerically equal to the
load between the
WO
points. The increment of bending moment balances the couple
formed by the shears on each side of the element. The signs in the
WO
equations depend
on the sign convention adopted for
W,
S
and
M.
It
is often more useful to express the equations in the alternative forms:
S=--JUJdX
(~.l~)
M=
"SSdx
The point
of
m~imum moment occurs when the slope of the bending moment
diagram is zero. Equation
7.12
indicates that this point coincides with the point of zero
shear, i.e. when
S
=I
0.

In this section
we
have considered the equilibrium of a
small
element and then
integrated. In the previous section we considered the equilibrium
of
a freebody of finite
size. The
two
results in each case depend only upon statics.

S:
a concentrated load is applied normal (or transverse) to the axis of
beam, a step occurs in the shear force diagram equal in magnitude to the
concentrated load.
Between oints of load application, the shear force
is
constant.
1
of a beam subjected
to
a uniformly distributed load, the shear force
linear.
In regions of a beam subjected to a linearly varyin load, the shear force
diagram is parabolic.
m
The points on the shear force diagram where the shear force
is
zero
correspond to the points where the bending moment is either a ~~imum or
a minimum.
transverse load a~plication, the bending mo~ent diagram
is linear.
B
In regions
of
a beam subjected to a uniformly distributed load, the bendin
subjected
to
a linearly varyin
concentrated transverse loads
agram changes direction (kinks).
a couple is applied, a step occu
12kN
20
kN
