Hall A.S., Archer F.E., Gilbert R.I. Engineering Statics
Подождите немного. Документ загружается.


ABCD is a bar inclined at
30"
to the horizontal (Figure
P7.2))
pinned at
A,
and supported at D on rollers which provide a reaction normal to the bar.
It
carries
a
horizontal force of
20
kN
at
B
and a vertical force
of
10
kN
at
C,
Find the
B.M.,
S.F. and A.F. at the mid-point of the bar.
A
For the beam shown in Figure
P7.3
find the B.M. and
S.F.
at
E.
20
kN/m
B
A
C
Calculate
M,
S
and Nat the mid-points of
AB
and BC
of
the beam of Figure
P7.4.
100
kN
Pipre
PZ
4
For the beam shown in Figure
P7.4,
find the bending moment and shear
force at the mid-point
of
segments AB,
BC,
CD, DE and EF.

For the beam
of
Figure
P7.6,
find
N
12
kN
20 kN
and
M
at
P,
Q
and
R,
and
S
at
Q.
my
is the S.F. indererminate at
P
A
B
and
R?
re
P76
For the beam
of
Figure
P7.7:
(i)
find
N,
S
and Mat
P
(ii) express
S
and
M
in each segment
of
the beam as a function of
x,
where
x
is
the distance from A.
260
kNm
For the beam
of
Figure
P7.8:
(i>
find
MA,
ME,
M,,
M,
(ii) find the shear force at A,
B,
just to the left of C, just above C,
just to the left of
E,
and just to the right
of
E
(iii) find the axial force in the portions AB, BC, and CD.
so
kN
80 kN
F
I
II
4m
I
A
semi-circular rigid beam is loaded as shown in Fi ure
P7.9.
Find the
bending moment and axial force at A,
B,
C
and
D.
Also
find the shear force
at A and B.
20
kN
20
kN
20
kN
A
G
beam shown in Figure
P7.1
(pa
For the beam shown in Figure
P73
(page
110):
(i) express
M
and
S
in terms of
x,
where
x
is
the distance from
A
.M
and S.F. diagrams for this beam.
.M.
diagram for the beam of Figure
P7.6
(pa
For the beam of Figure
P
.7
(page
11
1)
derive ex~ressions for
M
and
S
for
each of the segments
AB,
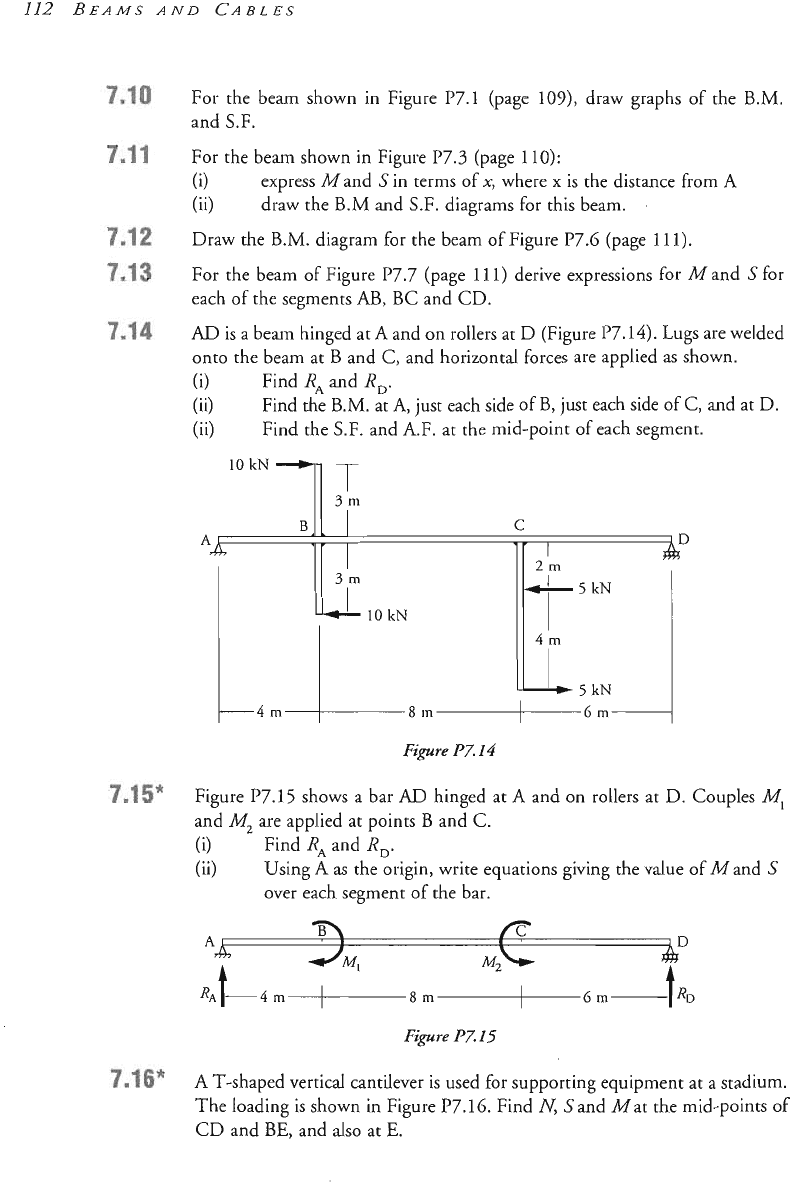
A
and
on rollers at
D
(Figure
P7.
14).
Lugs are welded
C,
and horizontal forces are applied as shown.
4m
8m
6
m”----
1-3
m-
E
40
kN
2 m+2
m-i
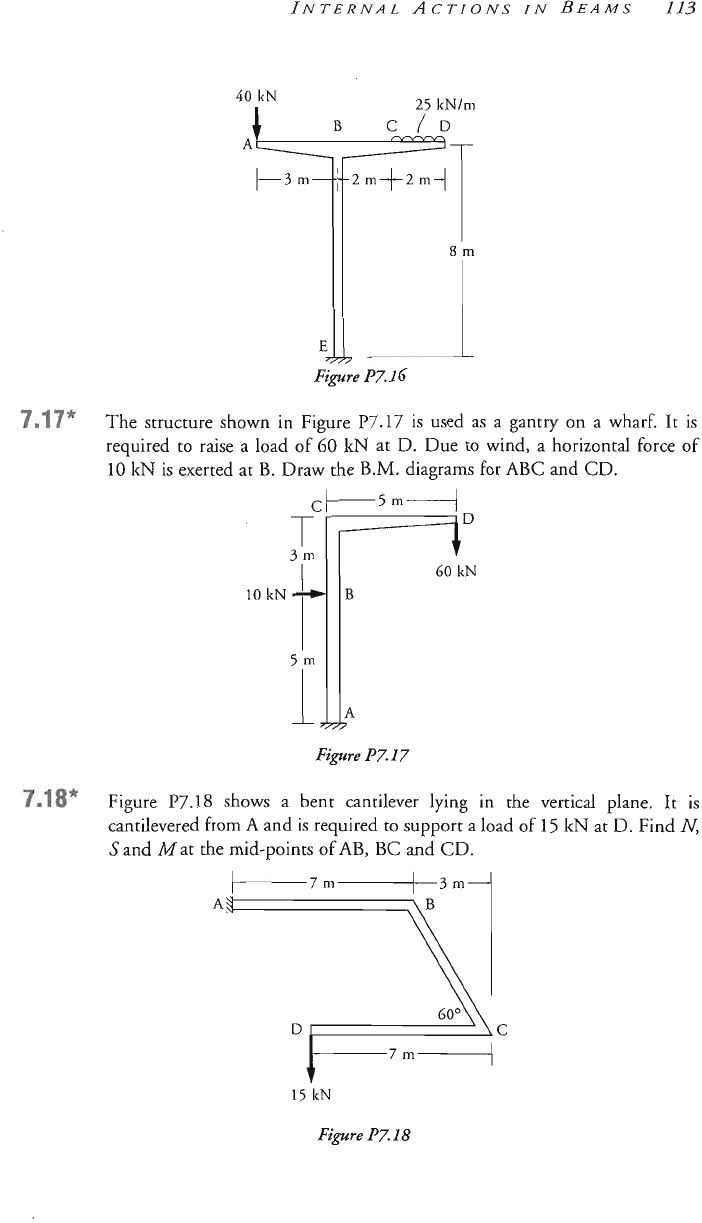
The stru~ture shown in Figure
P7.17
is
used
as a
ant^
on a wharf.
It
is
re~~ired
to
raise a load of
60
kN
at
R.
Due
to
wind,
a hori~ontal force
of
10
IkN
is
exerted at
10
kN
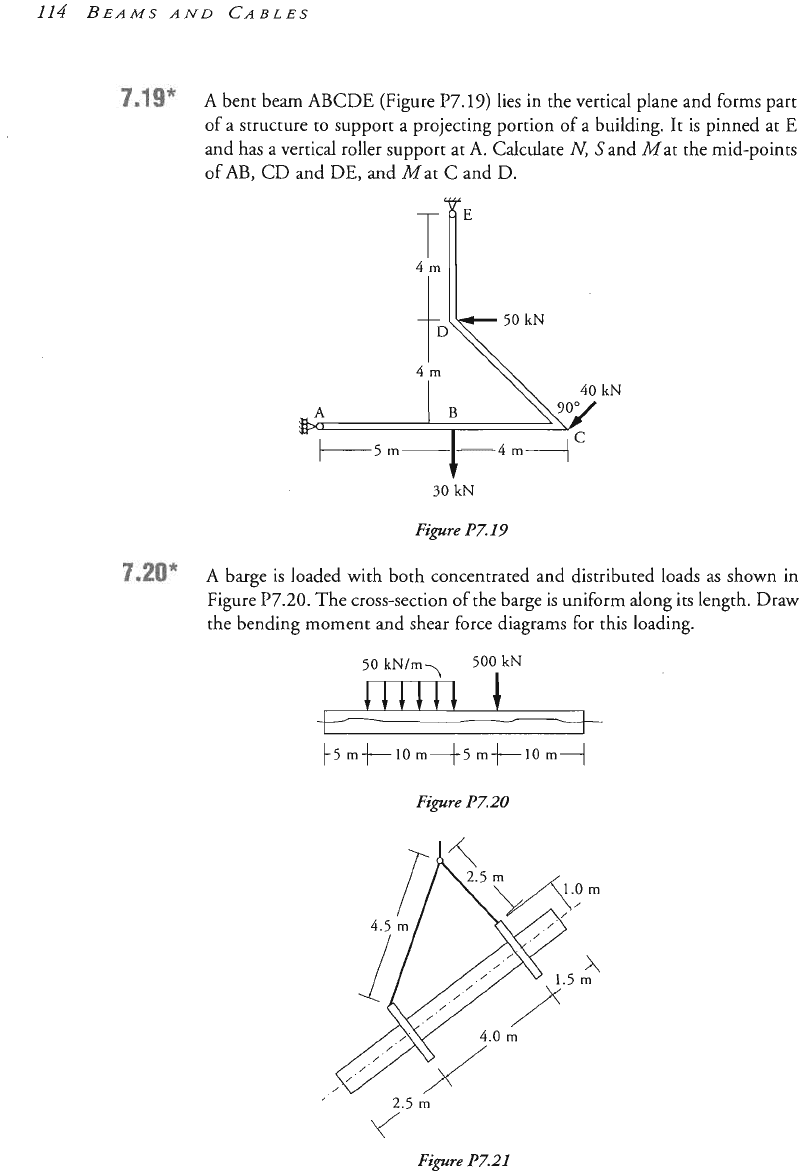
A
bent beam ABCDE (Figure
P7.19)
lies in the vertical plane and forms part
of a structure to support a projecting portion of a building. It is pinned at
E
and has a vertical roller support at
A.
Calculate
N,
S
and
M
at the mid-points
of
AB,
CD and DE, and Mat
C
and D.
4m
4m
li
E
SO
kN
kN
30
kN
A
barge
is
loaded with both concentrated and distributed loads as shown in
Figure
P7.20.
The cross-section of the barge is uniform along its length. Draw
the bending moment and shear force diagrams for this loading.
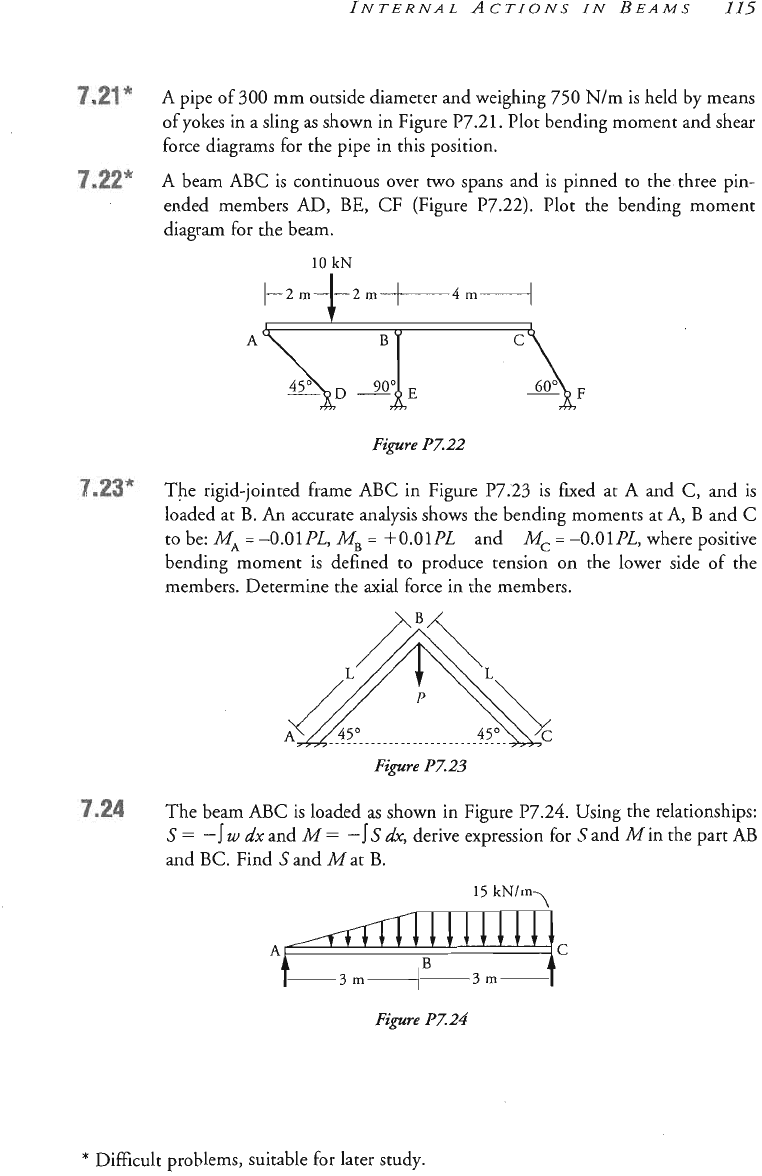
A pipe of
300
mm
outside diameter and weighing
750
Nlm
is held by means
of yokes in
a
sling
as
shown in Figure
P7.21.
Plot bending moment and shear
force diagrams for the pipe in this position.
A beam ABC is continuous over
two
spans and is pinned to the three pin-
ended members AD,
BE,
CF
(Figure
P7.22).
Plot the bending moment
diagram for the beam.
10
kN
Tfne rigid-jointed frame ABC in Figure
P723
is
fixed at A and C, and
is
loaded at
B.
h
accurate analysis shows the bending moments at A, B and
C
to be:
MA
=
-0.01
PL,
MB
=
+O.OIPL
and
MC
=
-O,OlPL,
where positive
bending moment is defined
to
produce tension on the lower side of the
members. Determine the axial force in the members.
Fipre
P723
The beam ABC
is
loaded
as
shown in Figure
P7.24.
Using the relations~ips:
S
=
--I
W
dx
and
M
=
--SS
h,
derive expression for
S
and
M
in.
the part AB
and BC. Find
S
and Mat B.
15
kN/m,
*
DiGcult problems, suitable for later study.


If a beam,
or
rigid bar, lies
in
one plane and supports loads in the same plane, it requires
at least three components of reaction to maintain it in eqLlilibriu~. If it
has
just three
riate reaction components, then these can be calculated from the e~ui~ibrium
equations
for
a
planar system
of
forces. The problems considered
in
Chapter
7
were
of
this type.
If the number of reaction components are too few the structure
will
be ~llstable, i.e.
it will
move
under certain types
of
load. The beam in Fi ure
8.
I
has
only
WO
reactions.
It
will
resist the load in Figure
8.
la,
but not that in Figure
8.
Ib,
and is therefore unstable.
W
W,
Even
if there are three reactions they must be
s~i~~~2~.
They
may
not be concurrent,
nor all parallel (i.e. concurrent at infinity). The structure of Fi ure
8.2a
will rotate about
A.
under the
load
shown (the three reactions are concurrent). The beam of
Fi
has
three reactions but if subjected to a horizontal load it
will
not be stable.
W
re
8.

118
BEAMS
AND
CABLES
If the beam has more than three reaction components, which is quite common in
practice, then the three equations of equilibrium applied to the complete beam are not
sufficient to evaluate these reactions, and additional information is required. Sometimes
this extra information is available in the form of a hown bending moment at some point
other than a support. For instance, the beam may contain one or more internal hinges.
If a hinge is assumed to be frictionless, the bending moment must be zero at that
location. It is then possible to consider the freebody to one side of the hinge and thus
obtain an extra equation.
For all reactions to be determined using only the principles of statics, the number
of
internal hinges must be the same
as
the extra number of equations required. For instance
a beam with five reactions must contain
two
hinges
so
that these
two
~~~~tiu~~
of
cu~~itio~,
together with the three equations of external equi~ibrium are equal to the
number of reactions. If there are more than
two
hinges (in this case) the beam is not
stable and will collapse under certain loads. If there are less than
two
hinges the reactions
cannot be determined by statics alone and the solution is not the subject
of
this book.
Such beams are not statically determinate.
A
beam such
as
that shown in Figure
8.3
may be used in bridge construction. It is often
more economical than
two
simply supported beams
AB
and
BC.
There are four
reactions, and these cannot be determined unless either the freebody
AD
or
DC
is
considered in addition to overall equilibrium, To avoid extensive arithmetic, it is
important to write the equilibrium equations in
a
suitable sequence.
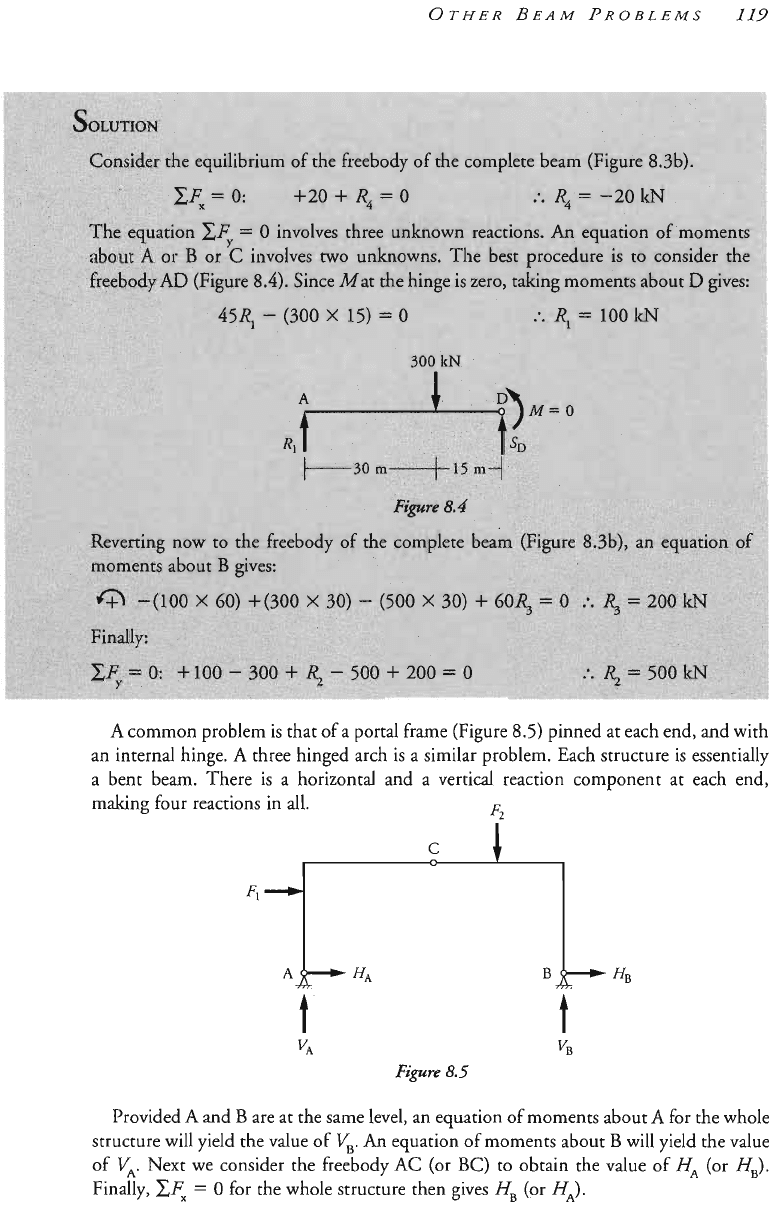
A co~~on problem is that of a portal frame (Figure
8.5)
pinned at each end, and with
an internal hinge.
A
three hinged arch is a similar problem. Each structure is essentially
a bent beam, There is a horizontal and a vertical reaction component at each end,
four reactions in
all.
F2
Provided A and B are at the same level, an equation of moments about A for the whole
structure will yield the value of
V,.
An
equation of moments about
B
will yield the value
of
V,.
Next we consider the freebody AC (or BC) to obtain the value of
HA
(or
H,).
==
0
for the whole structure then gives
HB
(or
H').
