Гусман Ю.А., Смирнов А.О. Математика: региональные олимпиады
Подождите немного. Документ загружается.

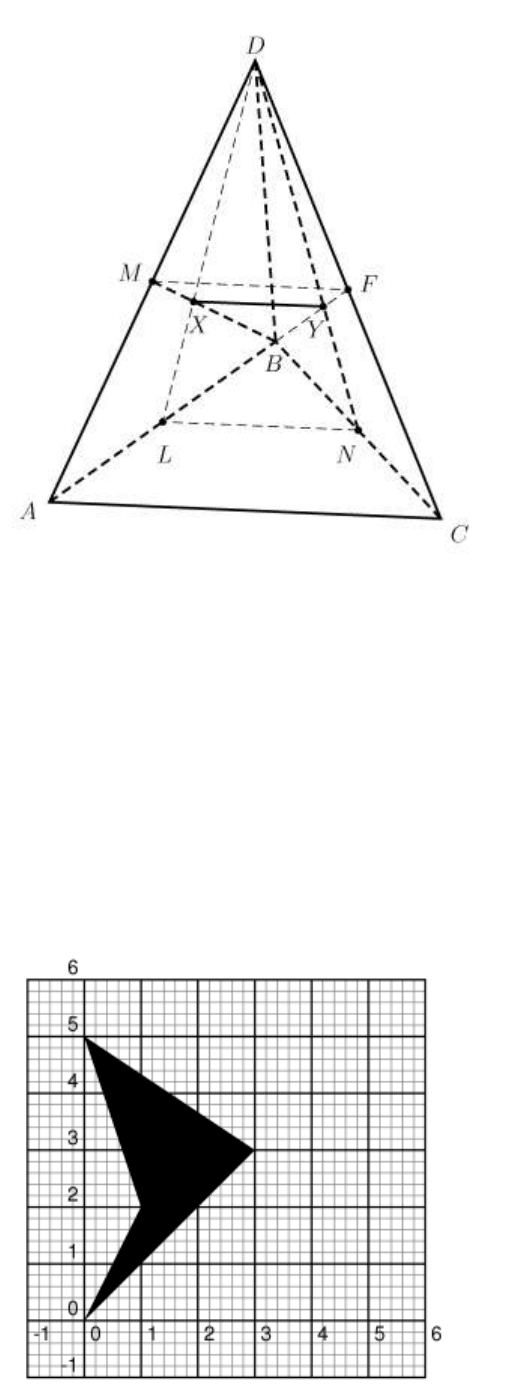
Рисунок 4.1. Тетраэдр.
Задача 4. Известно, что сумма трех положительных чисел равна 939.
На какое наибольшее число нулей может оканчиваться десятичная
запись произведения этих трех чисел?
Решение. Так как не более двух слагаемых может быть целыми
сотнями, то оптимальный вариант с наибольшим числом нулей в
окончании произведения искомых слагаемых может быть пять;
например, 500, 400, 39.
Ответ: 5.
Задача 5. Найдите площадь фигуры на рисунке
Рисунок 4.2. Многоугольник.
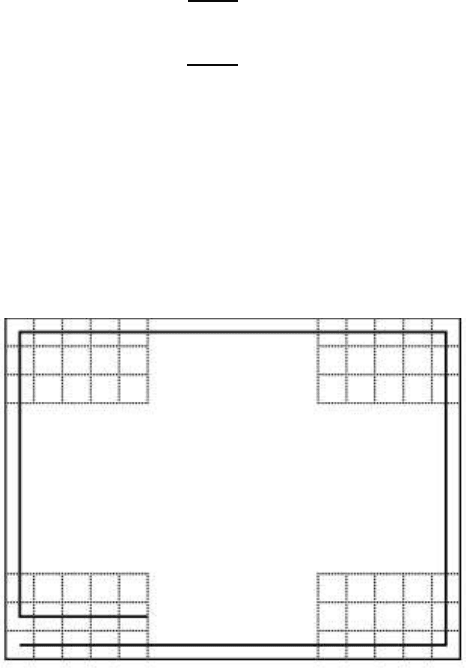
Решение. Площадь ABCD равна разности площадей треугольников
ACD и ACB.
Ответ: 5.
Задача 6. Клетки прямоугольника 333 закрашивают
последовательно – начиная с левой нижней и двигаясь по спирали
против часовой стрелки. Найдите номер строки и столбца клетки,
которая будет закрашена последней. (Например, левая нижняя клетка
стоит в 333-й строке и первом столбце.)
Рисунок 4.3. Движение по спирали.
Решение.
При 1-м обходе крайние закрашенные точки имеют координаты:
(333;1); (333;444); (1;444); (1;1).
При 2-м обходе (332;1); (332;443); (2;443); (2;2).
При 3-м обходе (331;2); (331;442); (3;442); (3;3).
…………………………………………….
При 166-м обходе (168;165); (168;279); (166;279); (166;166).
При 167-м обходе (167;166); (167;278).
Последняя закрашенная клетка имеет номер – 167 строки, 278 столбец.
Ответ: 167;278.
Объединенная межвузовская математическая олимпиада школьников
2011 года
Заочный тур (25.12.2010 – 31.01.2011). Вариант Б
Задача 1. Известно, что Какое наименьшее значение
может принимать выражение
?
Ответ: 72.
Задача 2. Число 409,6 трижды увеличили на а затем трижды
уменьшили на В результате получилось число 34,3. Найдите
Ответ: 75.
Задача 3. Объем треугольной пирамиды равен 54. Найдите объем
пирамиды с вершинами в точках пересечения медиан данной
пирамиды.
Ответ: 8.
Задача 4. Какое наименьшее количество цифр нужно написать
подряд, чтобы вычеркиванием некоторых цифр можно было получить
любое трехзначное натуральное число?
Ответ: 29.
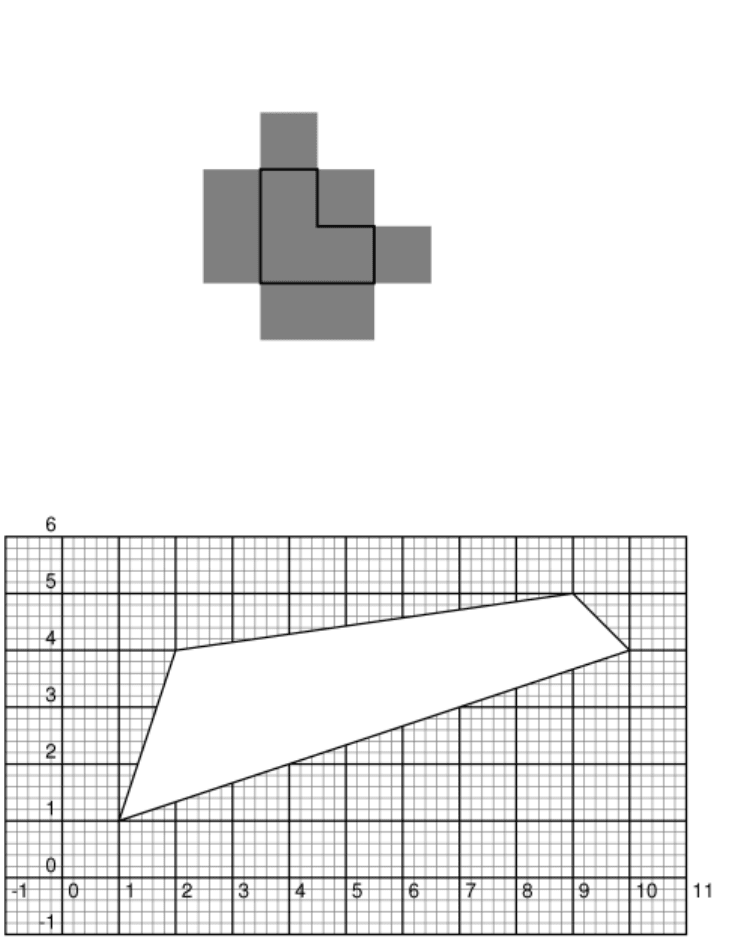
Задача 5. На клетчатой бумаге закрасили «уголок» из 3 клеток, после
чего 100 раз повторили следующую операцию: закрасить все клетки,
граничащие (по стороне) с какой-либо из уже закрашенных (см.
рисунок 4.4). Сколько всего закрашенных клеток (включая клетки
исходного уголка) получилось?
Рисунок 4.4. Закрашенные клетки.
Ответ: 20503.
Задача 6. Найдите координаты центра окружности, описанной около
четырехугольника на рисунке 4.5.
Рисунок 4.5. Четырехугольник.
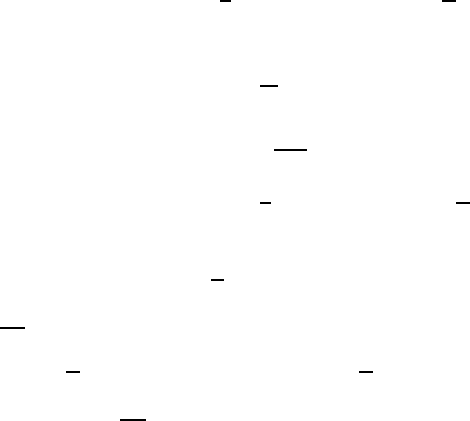
Ответ: (5,5;2,5).
4.2 Объединенная межвузовская математическая олимпиада
06.02. 2011
I вариант (с решением)
Задача 1. Решите уравнение
|
|
Решение. Очевидным корнем является
Рассмотрим два случая:
Тогда
(
)
Из этих значений выберем те, которые меньше единицы: такими будут
(
)
Если Тогда
(
)
Из этих значений выберем те, которые больше единицы: такими будут
. В итоге.
Ответ: 1;
(
) .
Задача 2. Ваня сдал три ЕГЭ. По русскому языку он набрал на 5
баллов меньше, чем по физике, а по физике – на 9 баллов меньше, чем
по математике. Золотая рыбка, приснившаяся Ване, обещала
выполнить любое количество желаний следующих видов:
*прибавить по баллу за каждый экзамен;
*за один экзамен (по выбору Вани) уменьшить баллы на 3, а за каждый
из двух остальных – увеличить на 1.
Рыбка выполняет желание, если при этом ни один результат не
превысит 100 баллов. Мог ли Ваня во сне набрать 100 баллов более
чем по одному экзамену?
Решение. Для того чтобы набрать более чем по одному экзамену 100
баллов, разность баллов за два этих экзамена должна стать нулевой. Но
разность баллов за любые два экзамена или не меняется, или меняется
на 4. А первоначально разность баллов не делится на 4 ни для любых
двух результатов экзамена. Поэтому во сне Ваня не мог набрать 100
баллов более чем по одному экзамену.
Ответ: Нет.
Задача 3. Одна тетрадь, 3 блокнота и 2 ручки стоят 98 рублей, а 3
тетради и блокнот – на 36 рублей дешевле 5 ручек. Сколько стоит
каждый из предметов, если тетрадь стоит четное число рублей?
(Каждый из этих предметов стоит целое число рублей.)

Решение. Пусть тетрадь стоит – рублей; блокнот - y рублей; ручка - z
рублей. Тогда
{
Умножая первое уравнение на 3 и вычитая из него второе, получаем:
Так как каждый из предметов стоит целое число рублей, то должно
делиться на 11, то есть кратно 11. Поэтому может быть равно 11, 22
или 33. Но из первого уравнения следует, что, чтобы было четным,
тоже должно быть четным. Значит И тогда
Ответ: 4;22;14.
Задача 4. Каждому из двух рабочих поручили обработать одинаковое
количество деталей. Первый выполнил работу за 8 часов. Второй
потратил больше 2 часов на наладку оборудования и с его помощью
закончил работу на 3 часа раньше первого. Известно, что второй
рабочий через 1 час после начала работы оборудования обработал
столько же деталей, сколько к этому времени первый. Во сколько раз
оборудование увеличивает производительность труда?
Решение. Обозначим за время, затраченное на наладку
оборудования. Второй рабочий работал на оборудовании
(
)
часов.
Если всего надо было обработать деталей, то производительность
первого рабочего в час
деталей, второго
Так как второй рабочий за час делал столько же, сколько первый за
(
)
часов, то
(
)
(
)(
)
Так как , то
Оборудование увеличивает производительность труда
Ответ: 4.
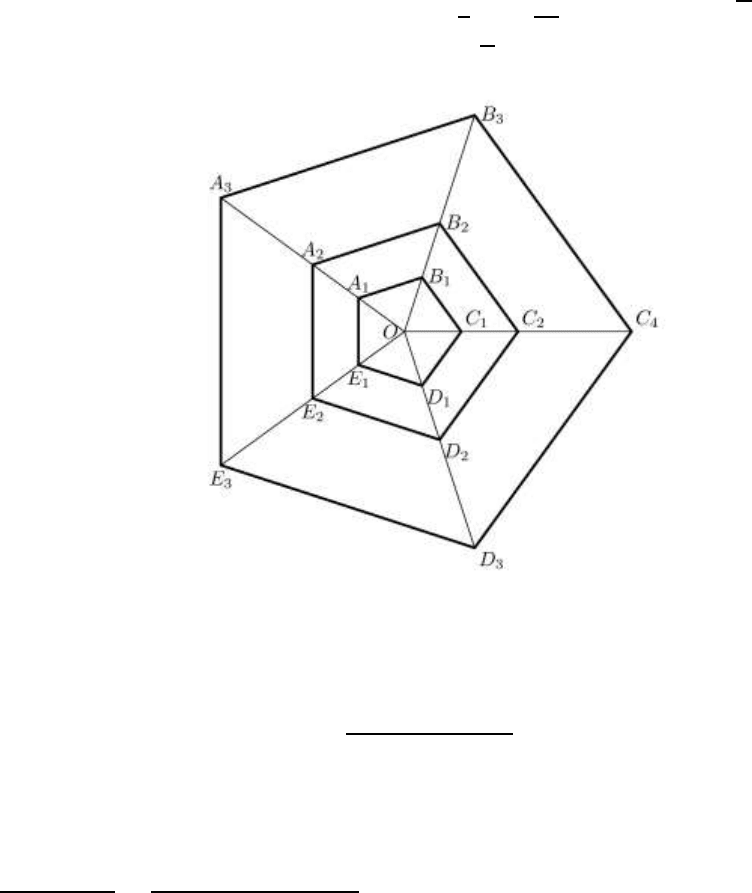
Задача 5. Три правильных пятиугольника имеют общий центр, их
стороны соответственно параллельны. Стороны двух пятиугольников
равны 4 см и 12 см. Третий пятиугольник делит площадь фигуры,
заключенный между первыми двумя, в отношении 1:3, считая от
меньшего пятиугольника. Найдите сторону третьего пятиугольника.
Решение. Так как пятиугольники подобны (рисунок 4.6), то достаточно
рассматривать подобные треугольники:
Пусть площадь треугольника
равна . Так как площади
подобных фигур относятся как квадраты сторон, то
(
)
Тогда
Учитывая соотношение площадей:
, и тогда
Обозначим
тогда
(
)
√
Ответ: 4
√
.
Рисунок 4.6. Правильные пятиугольники.
Задача 6. Функция такова, что
(
)
(
)
для всех x,y. Найдите все возможные значения выражения
(
)
(
)
(
)
(
)
Решение. При получаем
(
)
(
)
, или
(
)
(
)
Подставляя в искомое выражение, получаем:
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
=4.
Ответ: 4.
Задача 7.В равнобедренном треугольнике с периметром 60 см точка
пересечения медиан лежит на вписанной окружности. Найдите
стороны треугольника.
Решение. Так как точка пересечения медиан лежит на вписанной
окружности (рисунок 4.7), то где - радиус
вписанной окружности.
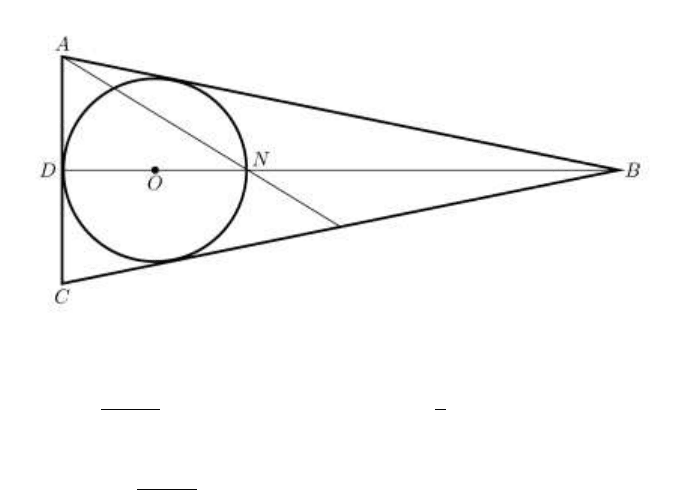
Рисунок 4.7. Равнобедренный треугольник.
Так как
или
(
)
Из сравнения получаем:
Тогда
Ответ: 25;25;10.
Задача 8. Решите систему
{
Решение. Возводя первое уравнение в квадрат и вычитая из него
второе, получим
(
)
Тогда
(
)
получаем:
(
)
Если
то
{
{
Если
то
{
Данная система решений не имеет.
Ответ: (4;3;6),(4;6;3).
Задача 9. На рисунке 4.8 изображен многогранник, все двугранные
углы которого прямые. Саша утверждает, что кратчайший путь по
поверхности этого многогранника от вершины X до вершины Y имеет
длину 4. Прав ли он?
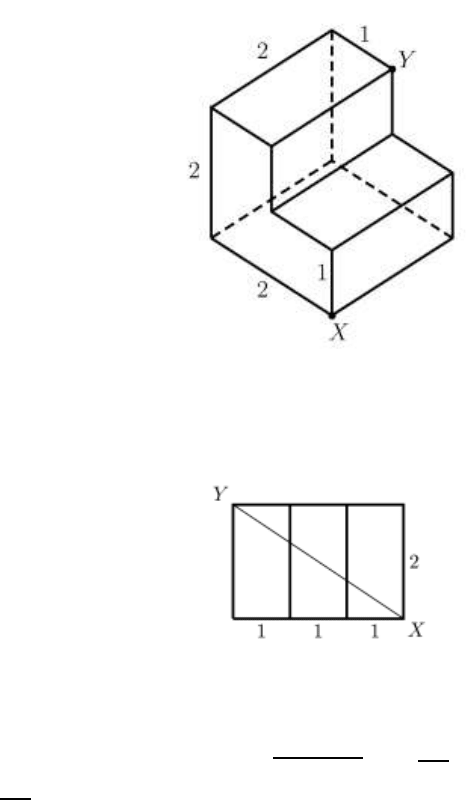
Рисунок 4.8. Многогранник.
Решение. Рассмотрим развертку трех правых граней (рисунок 4.9).
Рисунок 4.9. Развертка правых граней.
Соединим прямой точки X и Y. Полученный путь будет кратчайшим.
√
√
Так как
√
, то Саша неправ.
Ответ: Нет.
Задача 10. Плоская фигура W представляет собой множество всех
точек, координаты которых ( ) удовлетворяют неравенству:
(
|
|
|
|
|
|
)
Нарисуйте фигуру W и найдите ее площадь.
Решение. Так как и входят только под знаками модулей, то
нарисуем фигуру в первой четверти, а потом воспользуемся
симметрией.
Итак, пусть тогда
(
|
|
)
Преобразуем данное неравенство
(
|
|
)
(
|
|
)
(
|
|
)
Если 0 , то
(
)
Если , то
Изобразим полученную фигуру на рисунке 4.10 и далее симметрично
на другие четверти.
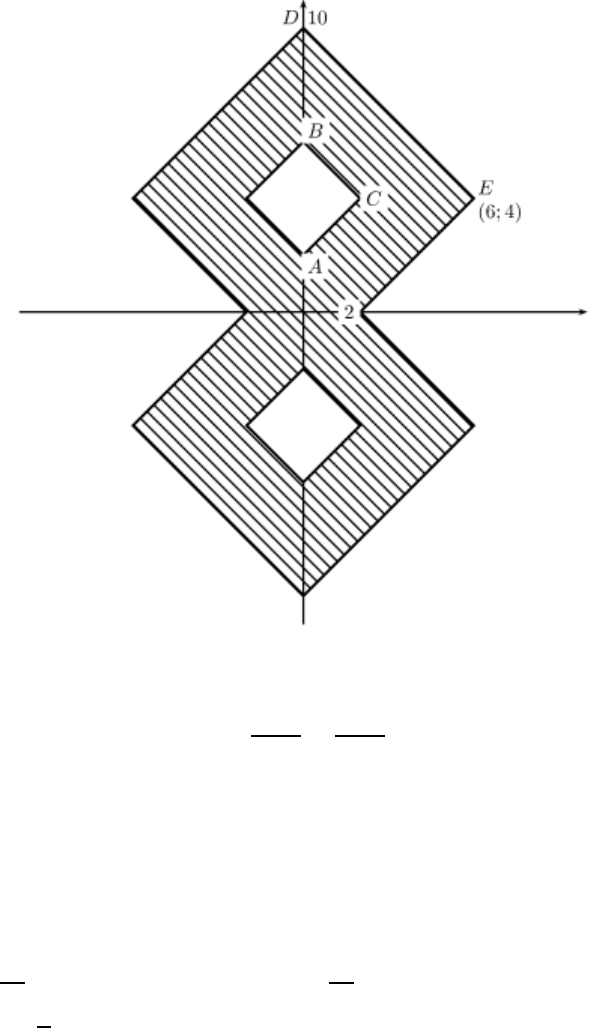
Рисунок 4.10. Плоская фигура W.
Вычислим площади, составляющие нашу фигуру:
Суммируя по всем четвертям, получим:
(
)
Ответ: 120.
II вариант
Задача 1. Решите уравнение
|
|
Ответ: -2;
.
Задача 2. Ваня сдал три ЕГЭ. По русскому языку он набрал на 3
балла меньше, чем по физике, а по физике – на 7 баллов меньше, чем
по математике. Золотая рыбка, приснившаяся Ване, обещала
выполнить любое количество желаний следующих видов:
*прибавить по баллу за каждый экзамен;
*за один экзамен (по выбору Вани) уменьшить баллы на 3, а за каждый
из двух остальных – увеличить на 1.
Рыбка выполняет желание, если при этом ни один результат не
превысит 100 баллов. Мог ли Ваня во сне набрать 100 баллов более
чем по одному экзамену?
Ответ: Нет.
Задача 3. Одна тетрадь, 3 блокнота и 2 ручки стоят 98 рублей, а 3

тетради и блокнот – на 36 рублей дешевле 5 ручек. Сколько стоит
каждый из предметов, если тетрадь стоит четное число рублей?
(Каждый из этих предметов стоит целое число рублей.)
Ответ: 4;22;14.
Задача 4. Каждому из двух рабочих поручили обработать одинаковое
количество деталей. Первый выполнил работу за 8 часов. Второй
потратил больше 2 часов на наладку оборудования и с его помощью
закончил работу на 3 часа раньше первого. Известно, что второй
рабочий через 1 час после начала работы оборудования обработал
столько же деталей, сколько к этому времени первый. Во сколько раз
оборудование увеличивает производительность труда?
Ответ: 4.
Задача 5. Три правильных восьмиугольника имеют общий центр, их
стороны соответственно параллельны. Стороны двух
восьмиугольников равны 7 см и 42 см. Третий восьмиугольник делит
площадь фигуры, заключенный между первыми двумя, в отношении
1:6, считая от меньшего восьмиугольника. Найдите сторону третьего
восьмиугольника.
Ответ: 7
√
.
Задача 6. Функция такова, что
(
)
(
)
для всех x,y. Найдите все возможные значения выражения
(
)
(
)
(
)
(
)
Ответ: 3.
Задача 7.В равнобедренном треугольнике с периметром 60 см точка
пересечения медиан лежит на вписанной окружности. Найдите
стороны треугольника.
Ответ: 25;25;10.
Задача 8. Решите систему
{
Ответ: (4;3;6),(4;6;3).
Задача 9. На рисунке 4.11 изображен многогранник, все двугранные
углы которого прямые. Саша утверждает, что кратчайший путь по
поверхности этого многогранника от вершины X до вершины Y имеет
длину 4,5. Прав ли он?
Ответ: Нет.
