Гусман Ю.А., Смирнов А.О. Математика: региональные олимпиады
Подождите немного. Документ загружается.

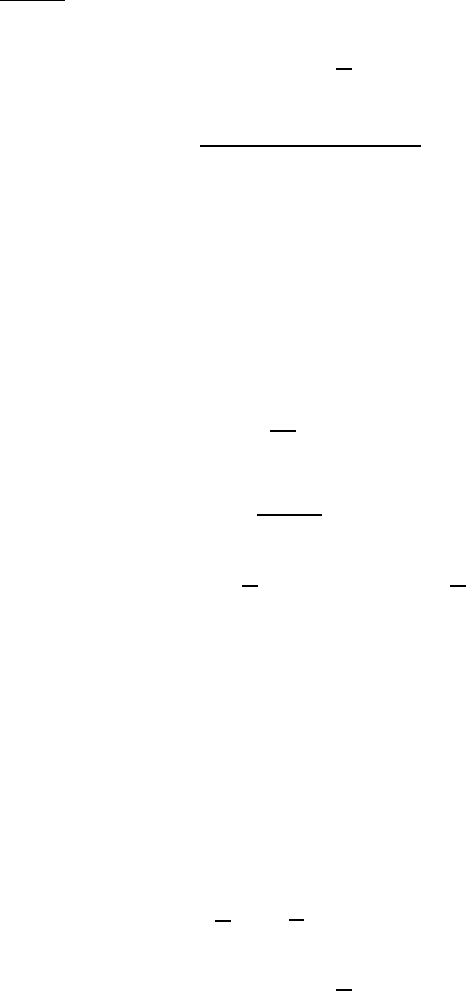
4. Решить уравнение
Ответ: 0,5;2.
5. При каких a сумма корней уравнения
ax 7=0 равна 6?
Ответ: -6.
6. Вычислить без калькулятора sin
Ответ: 1,5.
7. Найти наименьшее значение y, удовлетворяющее системе неравенств
{
Ответ: 1.
8. Найти наименьшее значение, удовлетворяющее неравенству
√
Ответ: 2.
9. Упростить и вычислить при
√
(
)
Ответ: 3.
10. Найти острый угол параллелограмма, если тупой равен
.
Ответ дать в градусах.
Ответ: 80.
Задание № Е-4 (2010)
1 тур региональной олимпиады (ГУАП)
1. Решить уравнение
(
) , если 9≤x
Ответ: 9;11.
2. Решить уравнение
(
)
.
Ответ: -2;4.
3. Решить уравнение 4
(
√
)
(
√
)
Ответ: 8;27.
4. Вычислить без калькулятора
Ответ: 0,51.
5. При каких a уравнение
|
|
=a имеет решение?
Ответ: [0; )
6. Вычислить без калькулятора
Ответ: 0,5.
7. Решить неравенство
Ответ: [-4;1].
8. Решить неравенство
√
√
Ответ: [2; )
9. Упростить и вычислить при
√
Ответ: 3.

10. Найти периметр квадрата, площадь которого равна 9.
Ответ: 12.
3.2 2-й тур олимпиады 2010 г.
Региональная олимпиада по математике
вузов Санкт-Петербурга (2010)
Задание № А-3 (с решением)
1. Решить уравнение
√
√
Решение: ООУ:
√
Обозначим
√
тогда уравнение примет вид:
√
√
(
)(
)
(
)(
)
Тогда
√
√
Ответ: 2;5.
2. Решить неравенство
|
|
|
|
Решение: дополнительное условие
√
Рассмотрим случай, когда тогда
|
|
и
неравенство принимает вид:
|
|
|
|
Если , то
Так как дискриминант квадратного трехчлена отрицателен, то
неравенство выполняется при любом x и, поэтому
Если же , то
Так как корни квадратного трехчлена
√
, причем меньший
корень
то получаем, что
Если
то
|
|
Если при этом
√
(дополнительное условие), то
В пределах нашей области получаем:
При
√
x>4.
Собирая полученные результаты, имеем:
Ответ:
(
)
(
)

3. Решить систему уравнений
{
Решение: преобразуем искомую систему уравнений, и вычтем из
второго уравнения первое, возведенное в квадрат:
{
(
)
{
(
)
{
(
)
(
)
{
(
)
Исключая из второго и третьего уравнений , получаем уравнение
относительно переменной x:
(
)
, получаем:
{
Решая по теореме Виета, получаем:
При
искомая система не имеет решений, так как из второго
уравнения следует, что
|
|
√
Ответ: (2;3;4);(2;4;3).
4. Решить уравнение
|
|
Решение: введя обозначение
получим:
|
|
два случая:
При получаем:
Предположению удовлетворяет только второй корень, поэтому
При получаем:
5y+4=0
Предположению удовлетворяет только второй корень, поэтому
Ответ: 0;2.
5. Найти сумму квадратов корней уравнения
(
)
Решение: ООУ:
√
√
√
Обозначим
тогда получим:
(
)
образим на рисунке 3.1 графики левой и правой частей
полученного уравнения. Так как функция в левой части монотонно
возрастает, а в левой – монотонно убывает, то возможна лишь одна
точка пересечения их графиков. Проверяем, что эта точка
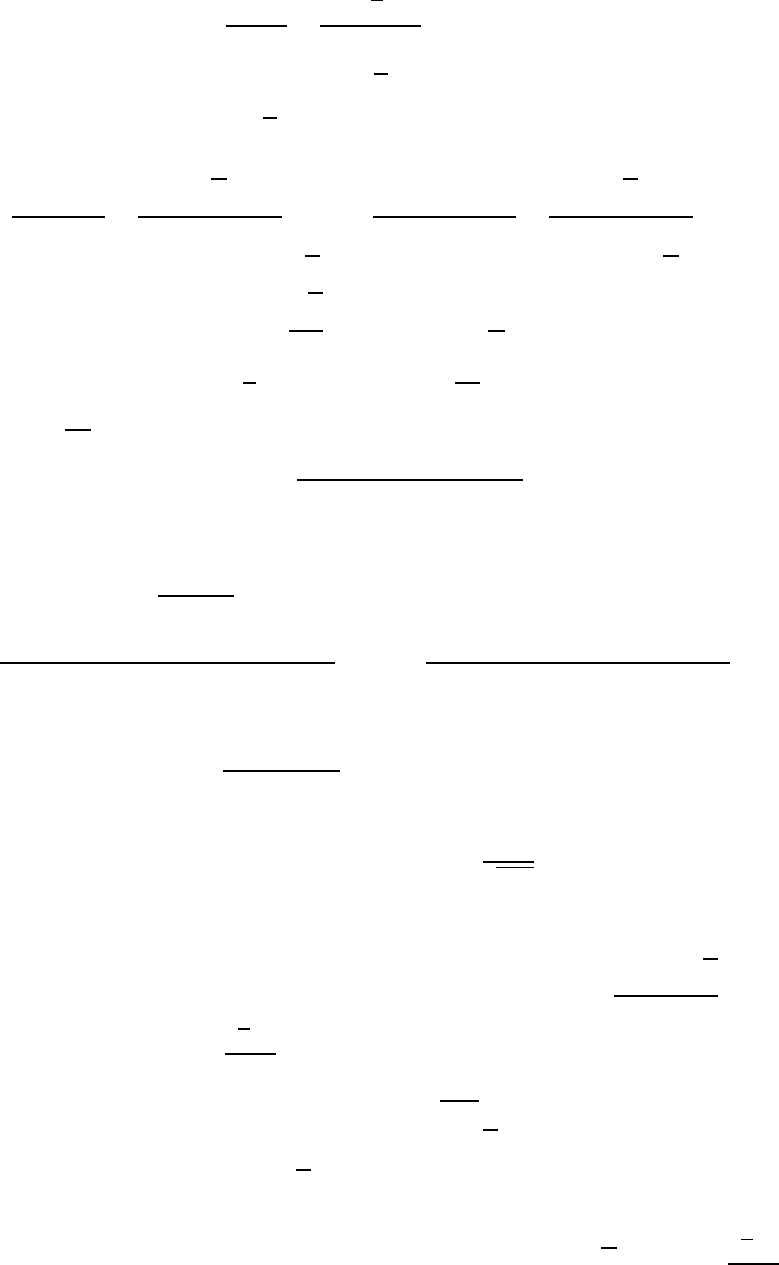
(
)
Таким образом
Сумма квадратов корней уравнения
Ответ: 10.
6. Решить уравнение
√
Решение: ООУ:
cos
Преобразуем уравнение
√
√
√
√
√
(
)
С учетом ООУ
(
)
Ответ:
7. Решить неравенство
(
)
(
)
Решение: ООН:
Преобразуем неравенство, пользуясь формулой
(
)
:
(
)
(
)
получим:
(
)
Решая неравенство, получаем:
Если то
√
(
)
(
)(
)
(
)(
)
(
)(
)
√
С учетом ООН:
√
Если то
√
С учетом ООН:
√
Если то
Собирая полученные результаты, имеем:
√
√

Ответ:
(
√
)
{
√
}
8. Найдите площадь фигуры, которая задается на координатной
плоскости системой неравенств:
{
Решение: точка А – точка пересечения прямых
{
имеет
координаты
(
)
точка B – точка пересечения прямых
{
имеет
координаты
(
)
точка C – точка пересечения прямых
{
имеет
координаты
(
)
Площадь треугольника АВС (рисунок 3.2) вычислим, как площадь
прямоугольника ДВFЕ за вычетом площадей треугольников АДВ,
BFC и СЕА:
Ответ: 4.
9. При каких значениях параметра a уравнение
(
)
(
)
имеет единственное решение?
Решение: в
получим:
(
)
(
)
. Дискриминант уравнения
(
)(
)
(
)(
)
(
)
При D=0
(
)
(
)
(не
удовлетворяет условию )
Если
(
)
(также не удовлетворяет
условию )
Если a=1, то (также не удовлетворяет условию )
Если уравнение имеет корни разных знаков, то по теореме Виета
Ответ:
(
)
(
)
10. Найти наибольшее значение функции
y=3cos3x+7cos2x-14cosx.
Решение: так как
а
(
)
(
)
то
подставляя эти значения, получаем функцию одной переменной:
(
)
(
)
Обозначив получим:
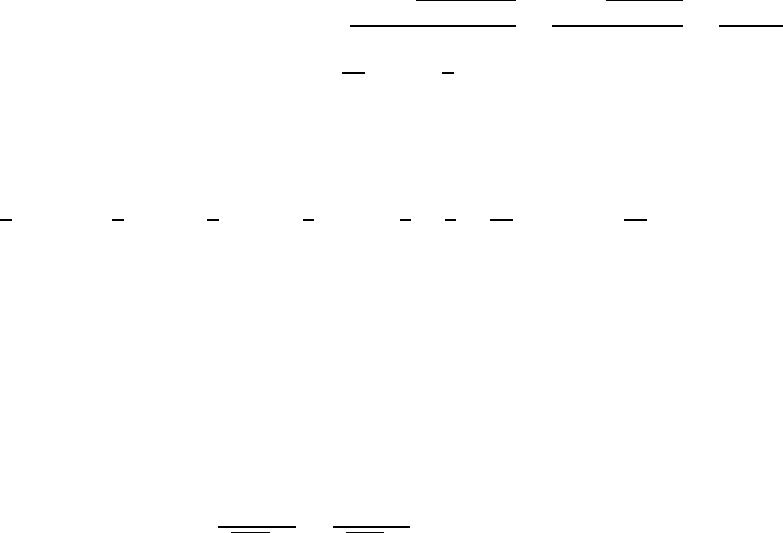
приведена к задаче нахождения
наибольшего значения данной функции на интервале [-1;1].
числим производную: y´=36
+28z 23.
Приравнивая производную нулю, найдем критические точки:
36
+28z 23=0
√
√
.
Из полученных корней
только второй
принадлежит искомому интервалу. Вычислим значения функции в
критической точке и на концах интервала и выберем наибольшее
значение.
y
(
)
y
(
)
y
(
)
Наибольшее значение равно 18.
Ответ: 18.
Региональная олимпиада по математике
вузов Санкт-Петербурга (2010)
Задание № А-4
1. Решить уравнение
√
√
Ответ: 7;39.
2. Решить неравенство
|
|
|
|
Ответ: (3;4)
(
)
3. Решить систему уравнений
{
Решение: введем обозначения: {
Тогда система примет вид:
{
Решим ее методом исключения неизвестных:
{
(
)
{
(
)
(
)
{
{
Таким образом, относительно первоначальных неизвестных система
имеет вид:
{

Перемножив все три уравнения, получим:
(
)
.
Ответ: (-2;-4;-5),(2;4;5).
4. Решить уравнение
|
|
Ответ: 1;3.
5. Найти сумму квадратов корней уравнения
(
)
Ответ: 5.
6. Решить уравнение
√
Ответ:
7. Решить неравенство
(
)
(
)
(
)
(
)
Ответ:
(
(
√
)
)
8. Найдите площадь фигуры, которая задается на координатной
плоскости системой неравенств:
{
Ответ: 10.
9. При каких значениях параметра a уравнение
(
)
(
)
имеет единственное решение?
Ответ:
(
]
{
}
[
)
10. Найти наименьшее значение функции
y=2cos3x-11cos2x+22cosx.
Ответ: -35.
Региональная олимпиада по математике
вузов Санкт-Петербурга (2010)
Задание № А-9
1. Решить уравнение
√
√
Ответ: 11;38.
2. Решить неравенство
|
|
|
|
Ответ: ( ;3)
(
)
3. Решить систему уравнений
{
(
)
(
)
(
)
Решение: преобразуем систему:

{
(
)
(
)
(
)
{
(
)
(
)
(
)
{
(
)(
)
(
)(
)
(
)(
)
Введем обозначения:
{
Тогда система примет вид:
{
Перемножив все три уравнения, получим:
(
)
.
:
{
{
:
{
{
Ответ: (-1;-3;-5),(1;3;5).
4. Решить уравнение 3
|
|
Ответ:
1.
5. Найти сумму квадратов корней уравнения
(
)
Ответ: 5.
6. Решить уравнение
√
Ответ:
7. Решить неравенство
(
)
(
)
Ответ:
(
√
)
(
)
8. Найдите площадь фигуры, которая задается на координатной
плоскости системой неравенств:
{
Ответ: 4.
9. При каких значениях параметра a уравнение
(
)
(
)
имеет единственное решение?

Ответ:
(
)
(
)
10. Найти наибольшее значение функции
y=2cos3x-11cos2x+22cosx.
Ответ: 14,5.
Региональная олимпиада по математике
вузов Санкт-Петербурга (2010)
Задание № А-10
1. Решить уравнение
√
√
Ответ: 6;11.
2. Решить неравенство
|
|
|
|
Ответ:
(
)
3. Решить систему уравнений
{
Ответ: (1;2;5),(1;5;2).
4. Решить уравнение 3
|
|
Ответ: 1;
3.
5. Найти сумму квадратов корней уравнения
(
)
Ответ: 5.
6. Решить уравнение
√
Ответ:
7. Решить неравенство
(
)
(
)
(
)
Ответ:
(
√
)
(
(
√
)
)
(
)
8. Найдите площадь фигуры, которая задается на координатной
плоскости системой неравенств:
{
Ответ: 10.
9. При каких значениях параметра a уравнение
(
)
(
)
имеет единственное решение?
Ответ:
(
]
{
}
[
)
10. Найти наименьшее значение функции
y=3cos3x-14cos2x+28cosx.
Ответ: -45.
4 Олимпиада по математике 2011 г.-
4.1 Объединенная межвузовская математическая олимпиада
школьников 2011 года
Заочный тур (25.12.2010 – 31.01.2011). Вариант А (с решением)
Задача 1. Известно, что
Найдите значение выражения
Решение. Так как
(
)(
)
(
)
(
)(
)
((
)
)
(
)
Ответ: 295.
Задача 2. Если бы Вася весь путь бежал со скоростью 8 км/ч, то он
бы как раз успел на поезд. Но Вася первую четверть пути бежал в 2
раза медленнее, чем надо. С какой скоростью Васе придется бежать
оставшуюся часть пути, чтобы успеть на поезд?
Решение. Обозначим весь путь за км.
Если бы Вася весь путь бежал со скоростью 8 км/ч, то он бы потратил
на весь путь
ч. На первую четверть пути Вася потратил
(
)
ч. На три четверти пути у него осталось
(
)
=
ч.
Пусть скорость с какой Васе придется бежать оставшуюся часть пути,
чтобы успеть на поезд – км/ч. Тогда
км/ч.
Ответ: км/ч.
Задача 3. В гранях и BCD тетраэдра ABCD провели медианы
BM и DN. На этих медианах выбрали точки и так, что
параллелен . Во сколько раз XY меньше AC?
Решение. В гранях и BCD тетраэдра ABCD проведем медианы
(рисунок 4.1) BM, DL и DN,BF. Точки пересечения медиан граней
и BCD обозначим и . Из подобия треугольников DXY и DLN
следует параллельность XY и LN. Из подобия треугольников BLN и
BAC следует параллельность AC и LN. Поэтому параллелен .
Других отрезков параллельных AC, имеющих конец отрезка на DN
быть не может, потому что параллельные отрезки будут иметь другой
конец обязательно на DL.
Так как медианы в пересечении отсекают одну треть, то
Так как LN – средняя линия в треугольнике ABC, то LN=
поэтому
Ответ: 3.
