Гуменникова Ю.В., Лаврусь О.Е., Хайруллина Р.Н. (сост.) Методические указания и контрольные задания по предмету Аналитическая геометрия для студентов первых курсов всех специальностей очной формы обучения
Подождите немного. Документ загружается.


51
29 вариант. а) Определить фокусы и полуоси эллипса 1
16925
22
=+
yx
. б) Составить
каноническое уравнение гиперболы, если действительная ось равна 16, а угол между
асимптотой и осью абсцисс определяется условием
4
3
=
ϕ
tg
. в) Составить каноническое
уравнение параболы, если расстояние от фокуса до вершины равно 3.
30 вариант. а) Составить каноническое уравнение эллипса, если большая полуось равна
26 и эксцентриситет
13
12
=
ε
. б) Составить каноническое уравнение параболы, если
расстояние от фокуса до директрисы равно 2.
в) Определить полуоси, фокусы и
асимптоты гиперболы
1
64225
22
=−
yx
.
Задание 13
Привести к каноническому виду уравнение кривой второго порядка
0
22
=++++ FEyDxCyAx
, определить тип линии и построить эту кривую (таблица 4).
Таблица 4
№
вар.
Коэффициенты уравнений кривой №
вар
Коэффициенты уравнений кривой
A C D E F A C D E F
1 1 1 –6 10 –15 2 1 4 0 –1 –5
3 2 0 8 –1 12 4 9 4 –54 –32 109
5 4 –9 –8 –36 –68 6 4 9 –40 36 100
7 9 –26 –54 –64 –127 8 3 3 –24 12 58
9 5 1 10 –6 –6 10 1 –1 6 0 8
11 1 7 6 –28 –12 12 3 –8 –6 –24 –36
13 9 4 18 –8 –19 14 2 0 –4 –1 –4
15 9 –4 –36 –8 –4 16 4 4 –12 4 –3
17 9 5 18 –30 9 18 36 –4 –72 16 –88
19 –4 9 16 18 29 20 4 36 –16 72 –92
21 9 4 54 8 49 22 1 4 –2 56 181
23 7 –2 –42 –16 17 24 9 –4 0 24 –72
25 –1 4 –4 8 –4 26 1 1 6 –4 0
27 1 1 –4 6 0 28 1 4 4 –16 –8
27 9 –4 –36 –8 –4 30 25 9 –100 54 –44
Решение типового варианта
Задание 11.
Построить кривые и записать их уравнения.
1. Окружность а) с центром в т.
)0;0(O
и радиусом 2
1
=R ;
б) с центром в т.
)3;2(
1
−O и радиусом 3
2
=R .
2. Эллипс а) с центром в т.
)0;0(O
и полуосями 2
1
=a и 4
1
=b ;
б) с центром в т.
)3;2(
1
−O и полуосями 3
2
=a и 1
2
=b .
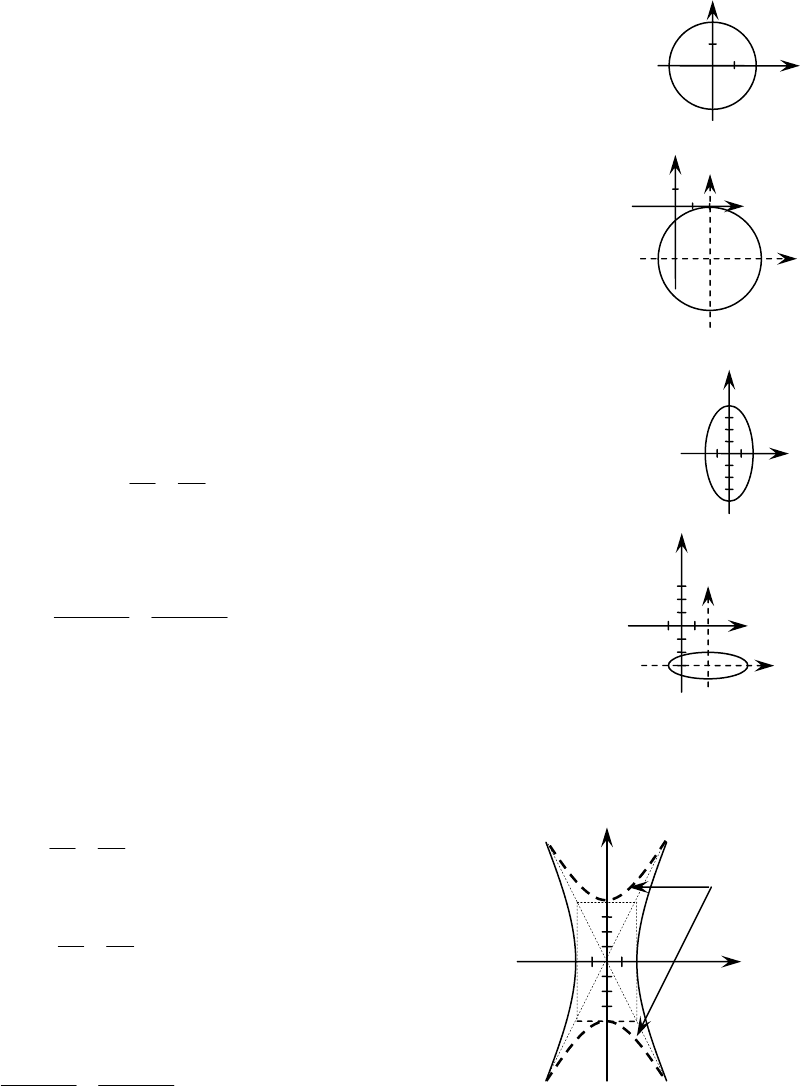
52
3. Гипербола а) с центром в т.
)0;0(O
и полуосями 2
1
=a – действительной, 4
1
=b –
мнимой и сопряженную с ней гиперболу;
б) с центром в т.
)3;2(
1
−O и полуосями 2
1
=a – действительной, 4
1
=b –
мнимой.
4. Парабола а) с вершиной в т.
)0;0(O
, параметром 4
1
=p , ветви которой
направлены
- вправо,
- влево,
- вверх,
- вниз;
б) с вершиной в т.
)3;2(
1
O и параметром 6
2
=p , ветви направлены вниз.
Решение.
1. Уравнение окружности с центром в т.
)0;0(O
и радиусом 2
1
=R составим
по формуле (1.3)
4
22
=+ yx
Уравнение окружности с центром в т.
)3;2(
1
−O и радиусом 3
2
=R
составим по формуле (1.4)
9)3()2(
22
=−+− yx
2. Уравнение эллипса с центром в т.
)0;0(O
и полуосями 2
1
=a и 4
1
=b
согласно формуле (2.1) имеет вид
1
164
22
=+
yx
.
Уравнение эллипса с центром в т.
)3;2(
1
−O и полуосями 3
2
=a и 1
2
=b по
формуле (2.2) имеет вид
1
1
)3(
9
)2(
22
=
+
+
−
yx
.
3. Уравнение гиперболы с центром в т.
)0;0(O
и полуосями 2
1
=a - действительной, 4
1
=b -
мнимой составим по формуле (3.1)
1
164
22
=−
yx
Сопряженная с ней гипербола описывается уравнением (3.2)
1
164
22
=+−
yx
Уравнение гиперболы с центром в т.
)3;2(
1
−O и полуосями
3
2
=a и 1
2
=b составим по формуле (3.3)
1
1
)3(
9
)2(
22
=
+
−
−
yx
1
1
х
y
x
y
1
1
x
y
1
1
y
1
х
1
1
1
x
y
Сопряженная
гипербола
1
1
х
y
х
1
y
1
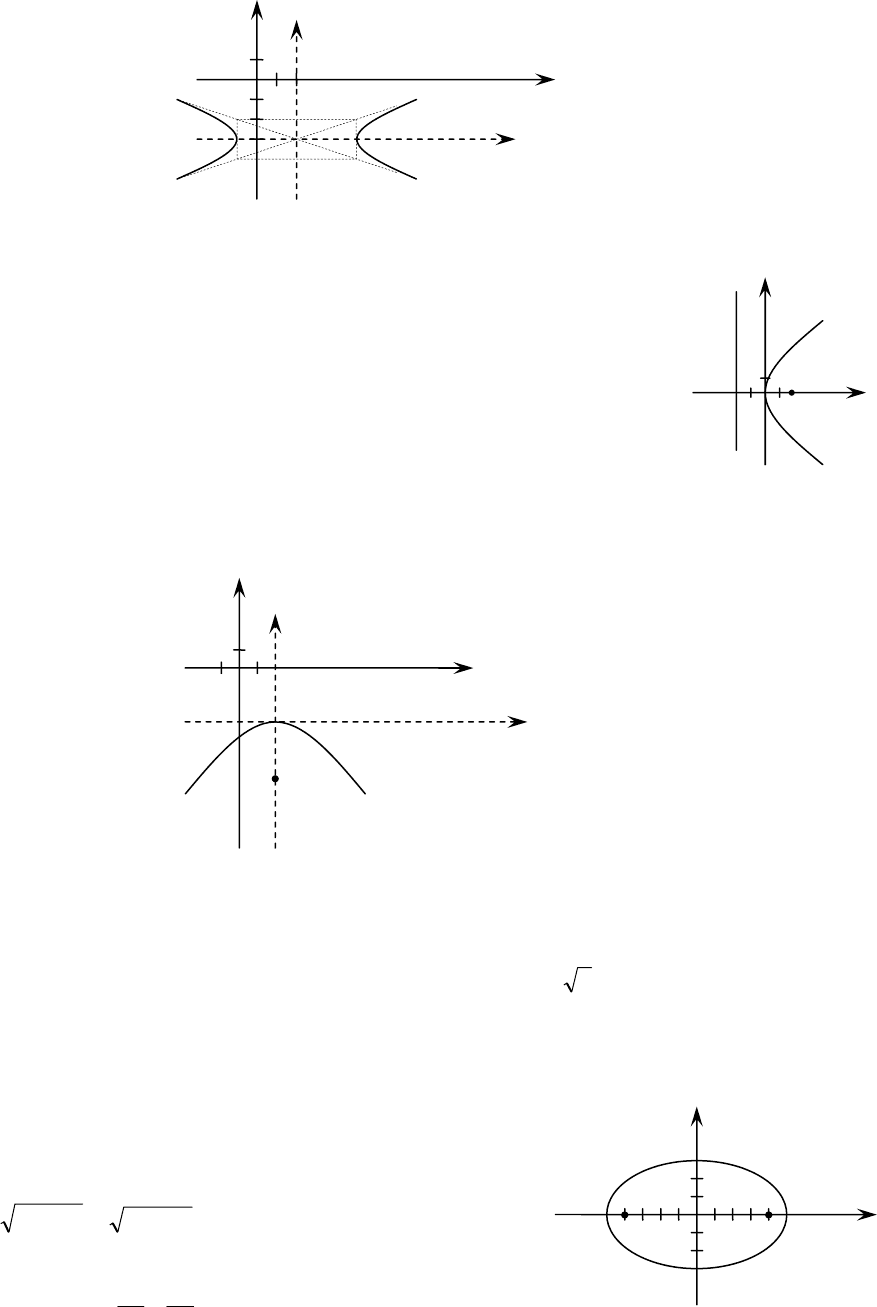
53
4. Уравнение параболы с вершиной в т.
)0;0(O
, параметром 4
1
=p ,
ветви которой направлены вправо, согласно формуле (4.1) имеет вид
xy 8
2
=
.
Уравнения подобных ей парабол с ветвями направленными влево,
вверх и вниз
xy 8
2
−=
,
yx 8
2
=
,
yx 8
2
−=
.
Уравнение параболы с вершиной в т. )3;2(
1
−O и параметром 6
2
=p ,
ветви которой направлены вниз согласно одной из формул (4.2) имеет вид
)2(12)3(
2
−−=+ yx
Задание 12. Составить канонические уравнения
а) эллипса, зная что его большая полуось равна 5, а расстояние между фокусами равно 8;
б) гиперболы, проходящей через т.
)3;5(−
с эксцентриситетом 2 ;
в) найти координаты фокуса и уравнение директрисы параболы
xy 4
2
−=
.
Решение.
а) Т.к. расстояние между фокусами эллипса
82 =c
, то
4=c
,
по условию
5=a
. Из формулы
222
bac −=
получаем
31625
22
=−=−= cab
Каноническое уравнение эллипса имеет вид (2.1)
1
925
22
=+
yx
.
б) Т.к. гипербола проходит через т.
)3;5(−
, то координаты этой точки удовлетворяют
каноническому уравнению гиперболы (3.1), т.е.
y
x
F
1
y
1
x
1
y
1
y
x
1
x
1
y
x
D
F 1
y
х
1
1
1
F
2
F
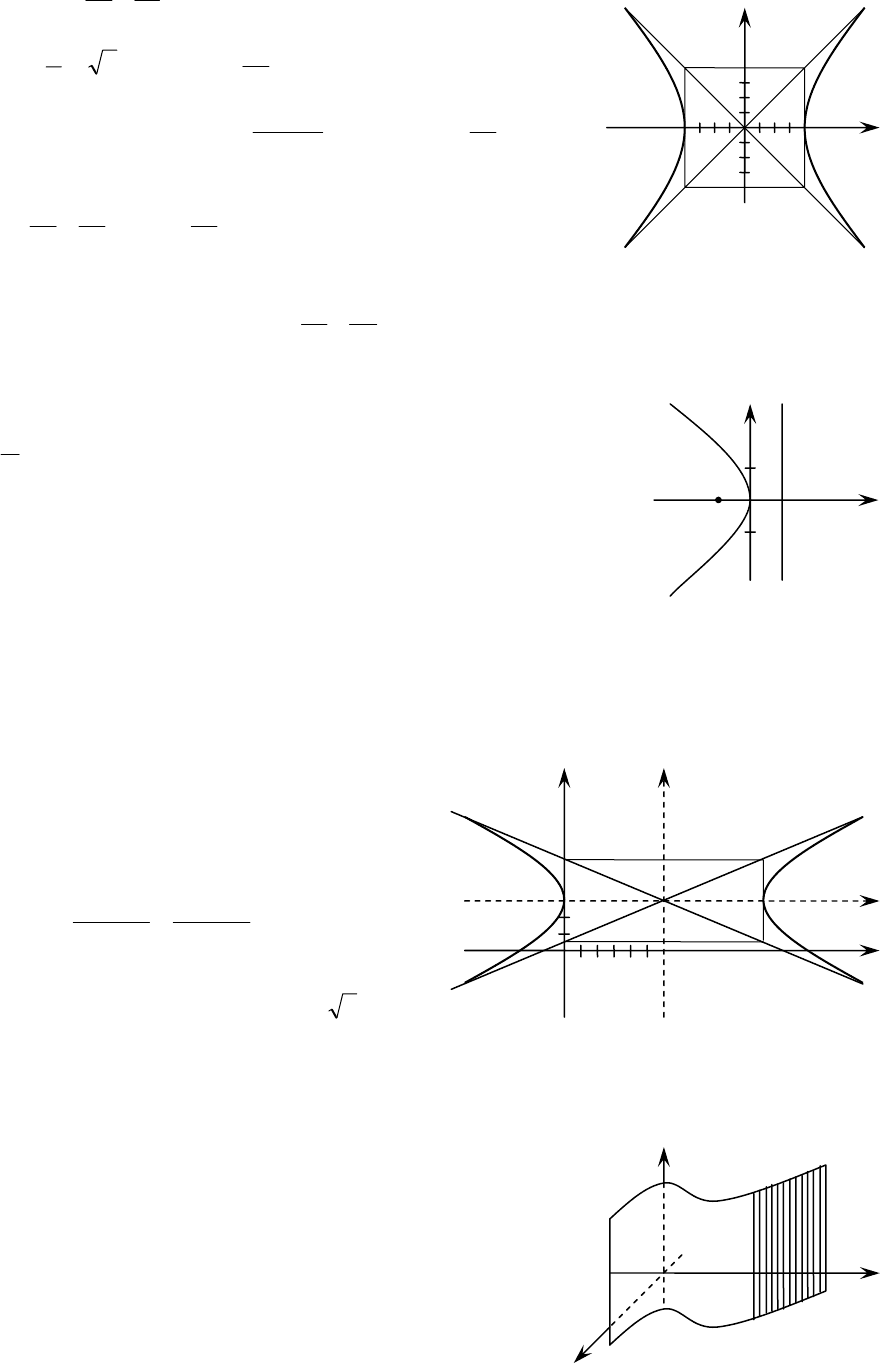
54
1
925
22
=−
ba
. (*)
По условию
2==
a
c
ε
, тогда 2
2
2
=
a
c
, учитывая, что для
гиперболы
222
bac +=
, получаем 2
2
22
=
+
a
ba
⇒ 21
2
2
=+
a
b
⇒
22
ba =
. Подставим последнее равенство в (*).
1
925
22
=−
aa
⇒
1
16
2
=
a
⇒
16
2
=a
.
Окончательно получаем:
1
1616
22
=−
yx
.
в) Из канонического уравнения параболы
xy 4
2
−=
видим, что
42 =p
;
2=p
;
1
2
=
p
(ветви направлены влево). Тогда уравнение
директрисы имеет вид:
1=x
,
фокус находится в т.
)0;1(−F
Задание 13.
Привести к каноническому виду уравнении кривой второго порядка, определить
тип линии и построить эту кривую.
05436126
22
=−+−− yxyx
.
Решение.
Дополним члены, содержащие
x
и y до
полных квадратов:
05454)96(636)3612(
22
=−++−−−+− yyxx
,
36)3(6)6(
22
=−−− yx
, 1
6
)3(
36
)6(
22
=
−
−
−
yx
.
Т.е. имеем гиперболу с центром в т.
)3;6(
1
O ,
действительная полуось
6=a
, мнимая
6=b
.
5. Цилиндры второго порядка. Конус второго порядка
Рассмотрим на плоскости
x
o
y
линию
L
с уравнением
0),( =yxF
. Через каждую точку
)0,,( yxM
этой линии
проведем прямую, параллельно оси
oz
. Все эти прямые
составят поверхность, называемую
цилиндрической или
цилиндром. Линия
L
называется направляющей этого
цилиндра, а каждая из прямых, параллельных оси
oz
–
образующей.
z
y
x
L
y
x
1
1
y D
x
1
1 F
y
x
y
x
6
3
1
1
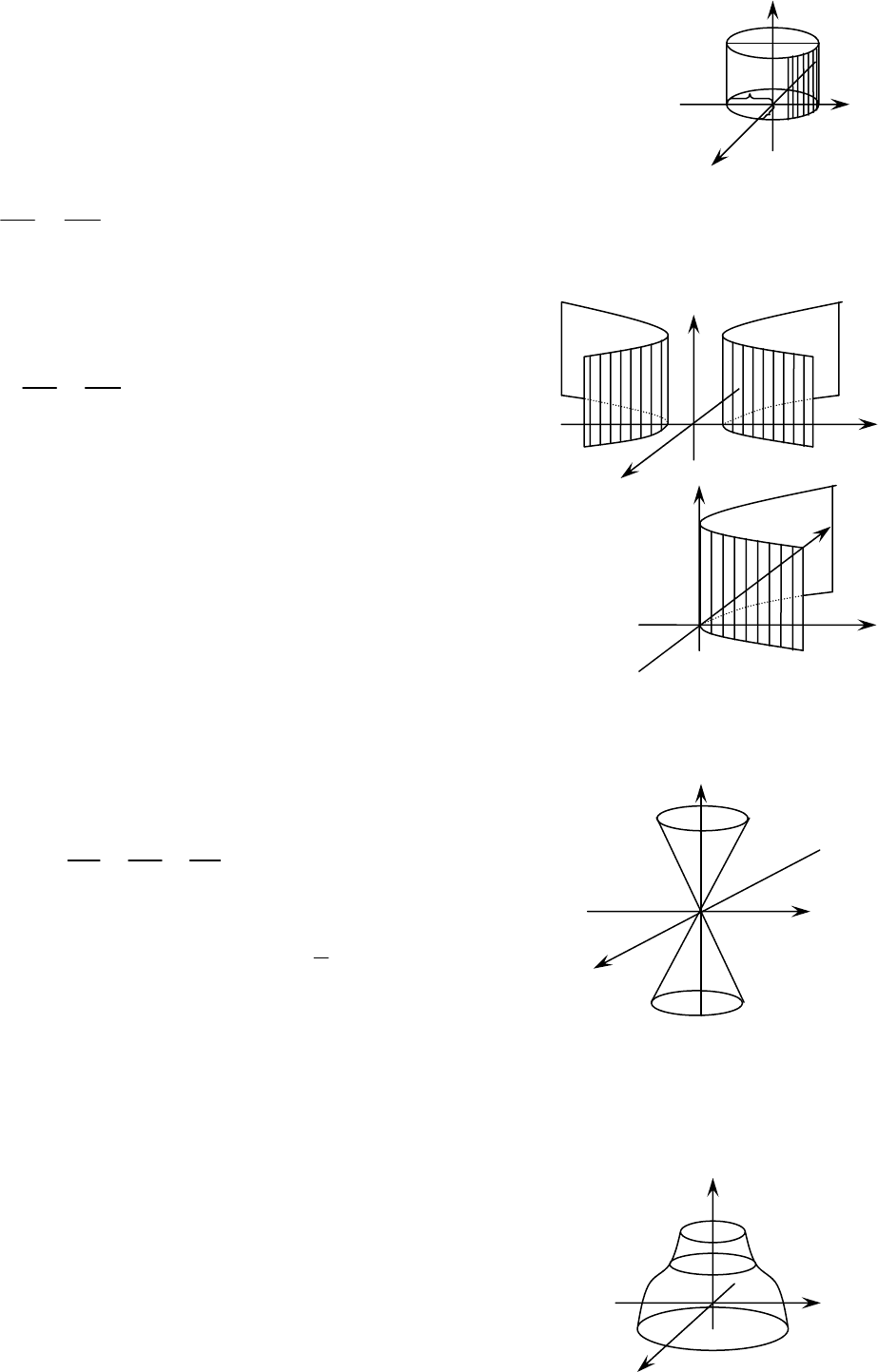
55
Уравнение
0),( =yxF
направляющей цилиндра, если
рассматривать его в пространстве, является уравнением самого
цилиндра. Цилиндр, направляющей которого служит кривая второго
порядка, называется
цилиндром второго порядка.
1. Эллиптический цилиндр
1
2
2
2
2
=+
b
y
a
x
(5.1)
2. Гиперболический цилиндр
1
2
2
2
2
=+−
b
y
a
x
(5.2)
3. Параболический цилиндр
pxy 2
2
=
(5.3)
Замечание ! Если уравнение поверхности второго порядка
имеет вид
0),( =zxF
или
0),( =zyF
, то это уравнение задает цилиндр с образующими,
параллельными оси
oy или
ox
соответственно.
Конус вращения.
0
2
2
2
2
2
2
=−+
c
z
b
y
a
x
(5.4)
получается при вращении прямой
y
a
c
z =
, расположенной в
плоскости
yo
z
, вокруг оси
oz
. Точка пересечения прямых,
составляющих конус (т.
О) называется вершиной конуса.
Линии, полученные при сечении конуса вращения различными плоскостями, называются
коническими сечениями или коники, это и есть кривые второго порядка: окружность,
эллипс, гипербола и парабола.
6. Поверхности вращения
Определение. Поверхности, получаемые вращением
некоторой плоской линии вокруг заданной оси координат,
лежащей с этой линией в одной плоскости, называются
поверхностями вращения.
z
y
x
b
a
z
y
x
z
x
y
z
y
x
z
x
y
56
Если линия лежит в плоскости yo
z
и имеет уравнение
0),( =zyF
,
0=x
, то при вращении
ее вокруг оси
oz
уравнение полученной поверхности вращения имеет вид:
0),(
22
=+± zxyF
(6.1)
Задание 14
Построить поверхности и определить их вид (название).
№ вар. а) б)
1
016164
222
=+−− zyx
04
2
=+ zx
2
0993
222
=−++ zyx
022
22
=−+ zyx
3
020105
222
=+−+− zyx
222
54 xzy =+
4
02484
222
=++− zyx
22
9zyx −=−
5
06
222
=+− zyx
2137
222
=−− zyx
6
22
48 yxz −−=
723694
222
=++ zyx
7
962464
222
=−+ zyx
222
208 xzy =+
8
040554
222
=+−− zyx
22
35 zxy +=
9
)(8
222
zyx +=
1832
222
=−+ zyx
10
xyz 1025
22
=+
060534
222
=+−− xyz
11
021147
222
=−−− zyx
22
42 zxy +=
12
01236
222
=−+− zyx
xzy =+
22
28
13
032416
222
=−++− zyx
036
222
=−+ zyx
14
015155
222
=+−− zyx
03
2
=+ zx
15
01866
222
=−++ zyx
033
222
=−+ zyx
16
021147
222
=+−+− zyx
222
62 xzy =+
17
01863
222
=−−+− zyx
22
2 zyx −=−
18
0364
222
=+− zyx
1234
222
=−− zyx
19
22
4 yxz −−=
484123
222
=++ zyx
20
601054
222
=−+ zyx
222
147 xzy =+
21
01669
222
=+−− zyx
22
61015 yxy +=
22
)(5
222
zyx +=
3632
222
=−+ zyx
23
xyx 1234
22
=+
012243
222
=+−− zyx
24
03228
222
=−−− zyx
22
34 xzy =−
25
0126
222
=−+− zyx
22
93 yzx =−
26
030532
222
=+−− zyx
032
2
=+ zx
27
042627
222
=−++ zyx
0542
22
=−+ zyx
28
0243124
222
=+−+− zyx
xzy 362
22
=+
29
02793
222
=++− zyx
22
42 xyz −=−
30
0216327
222
=+− zyx
42273
222
=−− zyx
57
Задание 15
Записать уравнение и определить вид поверхности, полученной при вращении данной
линии вокруг указанной оси координат, сделать рисунок.
№ вар. а) б)
1
zy 2
2
=
,
Oz
3649
22
=+ zy
,
Oy
2
1234
22
=− yx
,
Ox
1=x
,
2=y
,
Oz
3
zx 3
2
−=
,
Oz
1553
22
=+ zx
,
Ox
4
1243
22
=− yy
,
Oz
4=y
, 2=
z
,
Ox
5
yx 3
2
=
,
Oy
2443
22
=+ zx
,
Oz
6
1262
22
=− yx
,
Ox
zy 4
2
=
,
Oz
7
93
22
=+ zx
,
Oz
4=x
,
6=z
,
Oy
8
1553
22
=− zx
,
Oz
1−=z
,
3=y
,
Ox
9
zy 3
2
=
,
Oz
632
22
=+ zx
,
Ox
10
55
22
=− xy
,
Oy
3=y
, 1=
z
,
Ox
11
zx 4
2
−=
,
Oz
44
22
=+ zy
,
Oy
12
3065
22
=− yx
,
Ox
3=x
, 2−=
z
,
Oy
13
yz 2
2
=
,
Oy
632
22
=+ zx
,
Oz
14
zy 4
2
−=
,
Oz
63
22
=+ zy
,
Oy
15
3557
22
=− yx
,
Ox
1−=x
,
3−=y
,
Oz
16
zx =
2
2
,
Oz
44
22
=+ zx
,
Ox
17
1052
2
=− zy
,
Oz
2=y
,
6=z
,
Ox
18
yx 5
2
−=
,
Oy
632
2
=+ zx
,
Oz
19
99
22
=− yx
,
Ox
zy =
2
3
,
Oz
20
42
2
=+ zx
,
Oz
3=x
, 1−=
z
,
Oy
21
1315
22
=− yx
,
Ox
3=x
,
4=y
,
Oz
22
zy 5
2
=
,
Oz
2173
22
=+ yx
,
Ox
23
615
22
=+ xy
,
Oy
5=y
, 2=
z
,
Oy
24
2
5 xz −=
,
Oz
1183
22
=+ zy
,
Oy
25
28883
22
=− yx
,
Ox
5=x
,
3−=z
,
Oy
26
zy 72
2
=
,
Oz
3056
22
=+ zy
,
Oy
27
3575
22
=− yx
,
Ox
2=x
,
4−=y
,
Oz
28
zx 23
2
−=
,
Oz
21118
22
=+ yx
,
Ox
29
4085
22
=− zy
;
Oz
3=y
, 1=
z
,
Ox
30
yx 43 −=
;
Oz
1234
22
=+ zzx
;
Oz

58
Решение типового варианта
Задание 14. Построить данные поверхности и определить их вид (название):
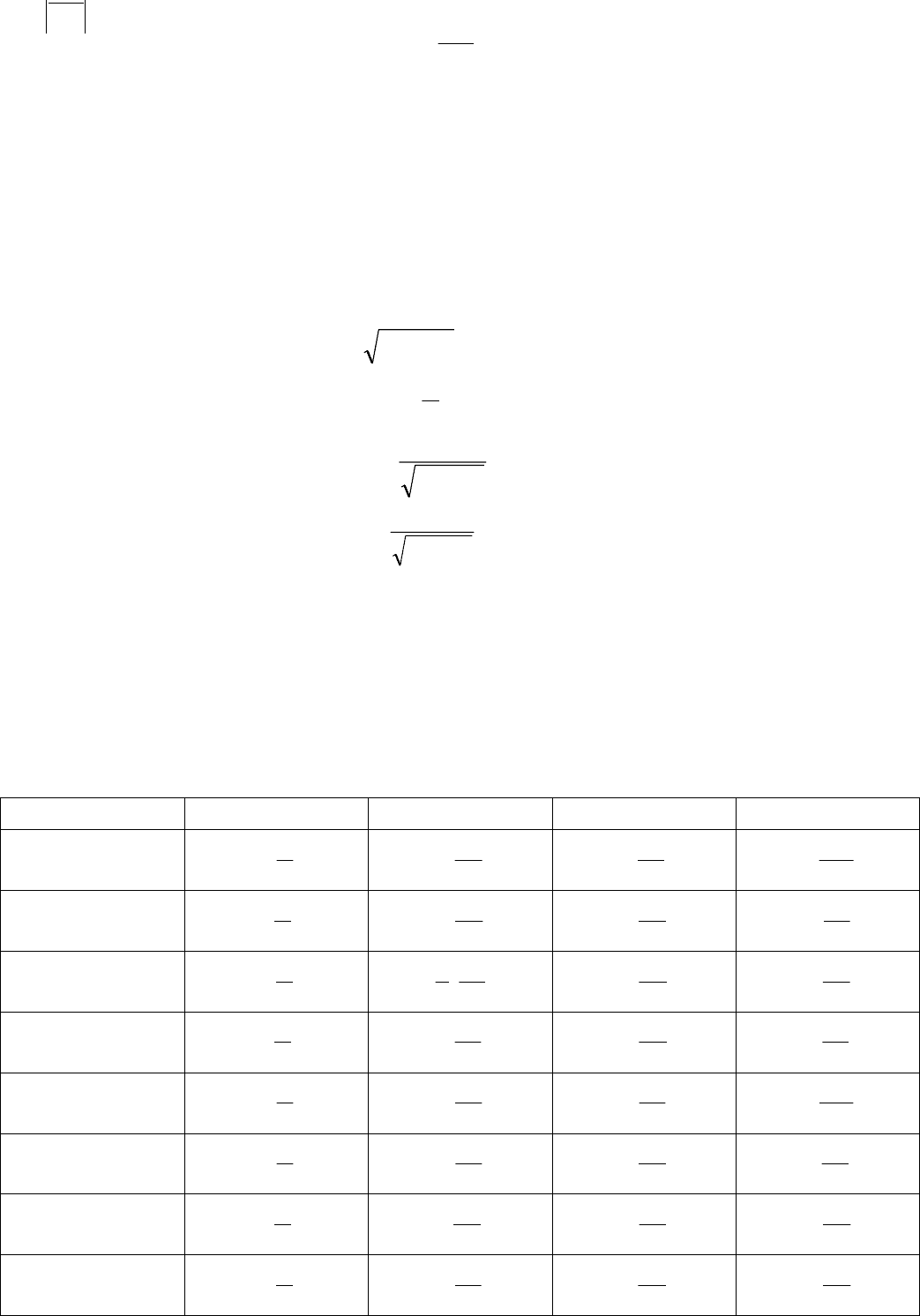
а)
02
3
2
4
2
2
2
=−+−
z
y
x
, б) 0
3
2
2
2
2
=+− z
y
x
Решение.
а) Приведем уравнение к каноническому виду, разделив его на 2:
1
618
222
=+−
zyx
.
Получили уравнение однополостного гиперболоида,
расположенного так, как показано на рисунке.
б) Приведем уравнение к каноническому виду
0
261
222
=+−
zyx
Это конус второго порядка, его сечения плоскостями
const
y
=
являются эллипсами.
Задание 15. Записать уравнение поверхности, полученной при вращении:
1) параболы
2
2 yz =
: а) вокруг оси
Oy
; б) вокруг оси
Oz
;
2) эллипса
1
416
22
=+
zx
: а) вокруг оси
Ox
; б) вокруг оси
Oz
.
Решение.
1. По формуле (6.1) получаем уравнение поверхности вращения:
а)
222
2yzx =+± ,
04
242
=+− zyx
. (алгебраическая поверхность четвертого порядка).
б)
(
)
2
22
2 yxz +±=
,
()
22
2 yxz +=
получим эллиптический параболоид (параболоид вращения)
2. Имеем
а)
(
)
1
416
2
22
2
=
+±
+
zy
x
, 1
4416
222
=++
zyx
.
Получим эллипсоид вращения (сфероид)
б)
(
)
1
416
2
2
22
=+
+±
z
yy
, 1
41616
222
=++
zyx
.
III. Линии, заданные уравнениями в полярных координатах
и параметрическими уравнениями
1. Полярные координаты точки и уравнение линии в полярных координатах
Для определения положения точки на плоскости,
кроме используемой выше декартовой системы координат
используется
полярная система координат. В ней
положение точки
M фиксируется с помощью расстояния
z
y
x
z
y
x
y
x
M
r
ϕ
59
OMr =
и угла
ϕ
, отсчитываемого против хода часовой стрелки от оси
Ox
, называемой
полярной осью, до радиуса – вектора OM . В этом случае используется запись
);(
ϕ
rM
.
Расстояние
r
называется полярным радиусом,
ϕ
– полярным углом точки M, а точка
O
– полюсом.
Связь между декартовыми
),( yx
и полярными
),(
ϕ
r
координатами т.
M
выражается
формулами:
⎭
⎬
⎫
⋅=
⋅=
.sin
,cos
ϕ
ϕ
ry
rx
(1.1)
Здесь
0≥r
;
π
ϕ
20 ≤≤
.
22
yxr +=
,
x
y
arctg=
ϕ
,
22
cos
yx
x
+
=
ϕ
, (1.2)
22
sin
yx
y
+
=
ϕ
.
Формулы (1.1) и (1.2) также позволяют переходить от уравнений линий, заданных в
декартовых координатах, к их уравнениям в полярных координатах, и наоборот.
Задание 16
Построить точки, заданные полярными координатами и найти их декартовы
координаты.
№ варианта
),(
111
ϕ
rM ),(
222
ϕ
rM
),(
333
ϕ
rM
),(
444
ϕ
rM
1
⎟
⎠
⎞
⎜
⎝
⎛
3
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;4
π
2
⎟
⎠
⎞
⎜
⎝
⎛
6
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;2
π
3
⎟
⎠
⎞
⎜
⎝
⎛
4
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
4
3
;
2
3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;5
π
4
⎟
⎠
⎞
⎜
⎝
⎛
3
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;3
π
5
⎟
⎠
⎞
⎜
⎝
⎛
3
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;5
π
6
⎟
⎠
⎞
⎜
⎝
⎛
6
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
3
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;1
π
7
⎟
⎠
⎞
⎜
⎝
⎛
4
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;4
π
8
⎟
⎠
⎞
⎜
⎝
⎛
3
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
4
3
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;2
π
60
9
⎟
⎠
⎞
⎜
⎝
⎛
6
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;2
π
10
⎟
⎠
⎞
⎜
⎝
⎛
4
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;4
π
11
⎟
⎠
⎞
⎜
⎝
⎛
3
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
4
3
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;3
π
12
⎟
⎠
⎞
⎜
⎝
⎛
6
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;1
π
13
⎟
⎠
⎞
⎜
⎝
⎛
4
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;1
π
14
⎟
⎠
⎞
⎜
⎝
⎛
6
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
4
3
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;5
π
15
⎟
⎠
⎞
⎜
⎝
⎛
4
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;3
π
16
⎟
⎠
⎞
⎜
⎝
⎛
4
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
3
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;5
π
17
⎟
⎠
⎞
⎜
⎝
⎛
3
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;2
π
18
⎟
⎠
⎞
⎜
⎝
⎛
6
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
3
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;2
π
19
⎟
⎠
⎞
⎜
⎝
⎛
3
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;1
π
20
⎟
⎠
⎞
⎜
⎝
⎛
6
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;4
π
21
⎟
⎠
⎞
⎜
⎝
⎛
6
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;3
π
22
⎟
⎠
⎞
⎜
⎝
⎛
4
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;1
π
23
⎟
⎠
⎞
⎜
⎝
⎛
6
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
5
;5
π
24
⎟
⎠
⎞
⎜
⎝
⎛
4
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;4
π
25
⎟
⎠
⎞
⎜
⎝
⎛
3
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
4
3
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;4
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;1
π
26
⎟
⎠
⎞
⎜
⎝
⎛
6
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
4
3
;
2
3
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;3
π
27
⎟
⎠
⎞
⎜
⎝
⎛
4
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
3
2
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;4
π
28
⎟
⎠
⎞
⎜
⎝
⎛
3
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;5
π
⎟
⎠
⎞
⎜
⎝
⎛
3
4
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;5
π
29
⎟
⎠
⎞
⎜
⎝
⎛
4
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;3
π
⎟
⎠
⎞
⎜
⎝
⎛
6
7
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
6
11
;2
π
30
⎟
⎠
⎞
⎜
⎝
⎛
3
;1
π
⎟
⎠
⎞
⎜
⎝
⎛
6
5
;
2
3
π
⎟
⎠
⎞
⎜
⎝
⎛
4
5
;2
π
⎟
⎠
⎞
⎜
⎝
⎛
4
7
;3
π
