Гуменникова Ю.В., Лаврусь О.Е., Хайруллина Р.Н. (сост.) Методические указания и контрольные задания по предмету Аналитическая геометрия для студентов первых курсов всех специальностей очной формы обучения
Подождите немного. Документ загружается.

31
4) по формуле (3.4) получаем:
01223)2(
2
3
3 =+−⇒+=− yxxy
- общее уравнение прямой.
6,4,1
64
=−=⇒=+
−
ba
yx
;
2
3
,
2
123
=⇒
+
= k
x
y
.
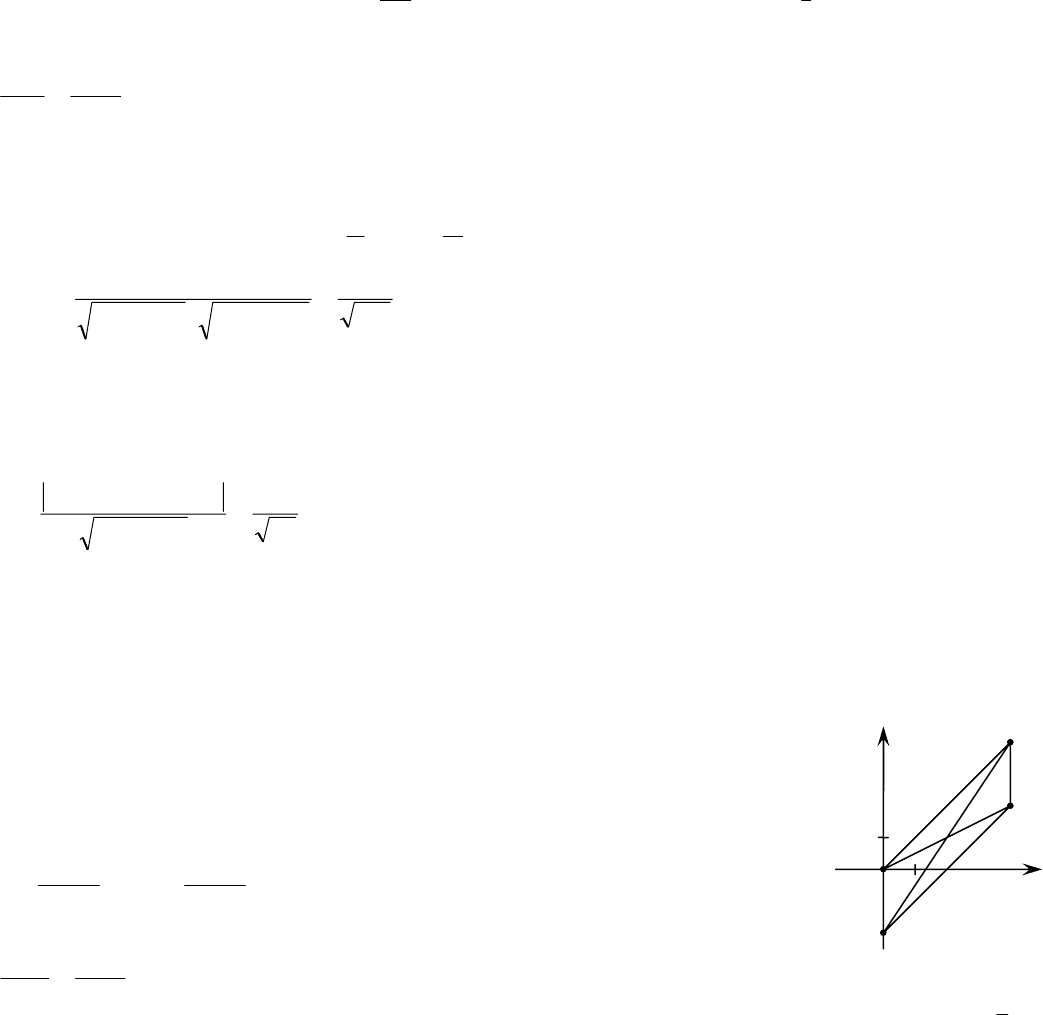
Задание 9.
Даны вершины треугольника
ABC
:
)2;3(A
,
)1;2(−B
,
)2;1( −C
. Построить треугольник и
найти:
1)
уравнение стороны
A
B и
AC
;
2)
уравнение высоты
CH
;
3)
уравнение медианы
A
M ;
4)
точку
N
пересечения медианы
A
M и высоты
CH
;
5)
уравнение прямой, проходящей через вершину
C
параллельно стороне
AB
;
6)
угол
ABC
;
7)
длину высоты
CH
.
Решение:
1) Для стороны
A
B воспользуемся формулой (3.7)
21
2
32
3
−
−
=
−−
−
yx
,
откуда
)2(5)3(1 −−=−− yx
или
075 =+− yx
. Аналогично выводится уравнение стороны
AC
:
4
2
2
3
−
−
=
−
−
yx
, откуда
042 =−− yx
.
2) Т.к. для высоты
CH
вектор
)1;5( −−AB
является
нормальным
n то пользуемся уравнением (3.2)
0)2(1)1(5 =+−−− yx
,
откуда
035 =−+ yx
.
3) Находим координаты точки
М – середины отрезка ВС:
5,0
2
12
−=
+−
=
M
x
;
5,0
2
21
−=
−
=
M
y
.
Уравнение медианы
A
M составим по формуле (3.7):
25,0
2
35,0
3
−−
−
=
−−
−
yx
;
)2(5,3)3(5,2 −−=−− yx
,
откуда
0175 =−− yx
.
4) Для нахождения координат точки
N
пересечения медианы
AM
и высоты
CH
составляем систему уравнений:
⎭
⎬
⎫
=−−
=−+
0175
,035
yx
yx
.
Решая ее, получаем
⎟
⎠
⎞
⎜
⎝
⎛
4
1
;
20
11
N
.
y
x
6
-4
1
1
А
H
C
B
M
N
x
y
1
1
32
5) Для искомой прямой вектор
)1;5( −−AB
является направляющим s , поэтому пользуемся
формулой (3.5)
1
2
5
1
−
+
=
−
−
yx
,
откуда
0115 =−− yx
.
6) Угол
ABC
найдем как угол между прямыми
A
B :
075 =+− yx
и
AC
:
042 =−− yx
по
формуле (3.9) учитывая, что
)5;1(
1
−n
,
)1;2(
2
−n
:
61,0
130
7
)1(2)5(1
)1()5(21
cos
2222
≈=
−+⋅−+
−⋅−+⋅
=
ϕ
,
o
52≈∠ABC
.
7) Длину высоты
CH
найдем как расстояние от точки
)2;1( −C
до прямой
A
B :
075 =+− yx
по формуле (3.11):
53,3
26
18
)5(1
7)2()5(11
22
≈=
−+
+−⋅−+⋅
=d
(ед.).
Задание 10.
Известны вершины
)0;0(O
и
)2;0( −A
параллелограмма
OACD
и точка
пересечения его диагоналей
)1;2(B
. Записать уравнение сторон параллелограмма.
Решение:
Уравнение стороны
ОА видно из построении:
ОА:
0=x
.
Т.к. точка
В является серединой диагонали AD, то по формулам
деления отрезка пополам получаем координаты вершин
D:
2
0
2
D
x+
=
;
2
0
21
D
x+
−=
4 ;4 ==⇒
DD
yx .
Уравнение стороны
ОD составим по формуле (3.7):
04
0
04
0
−
−
=
−
−
yx
, откуда получим
0=− yx
.
Уравнение стороны
АС находим, учитывая, что она параллельна прямой OD с
)1;1( −n
,
воспользовавшись формулой (3.2):
0)2(1)0(1 =+−− yx
, откуда
02 =−− yx
.
Наконец, учитывая параллельность стороны
ОА и DC составляем уравнение стороны DC:
4=x
.
Дополнительные задания
1 вариант
1. Даны уравнения двух сторон параллелограмма
02 =− yx
,
01 =−− yx
точка
пересечения его диагоналей
M(3;–1). Найти уравнения двух других сторон.
2.
Записать уравнения прямой в канонической форме:
⎩
⎨
⎧
=+−−
=−++
0632
022
zyx
zyx
y D
B
C
A
O
1
1
x

33
3. Написать уравнения плоскости, проходящей через точку
)3;7;2(
0
M
перпендикулярно прямой, которая через точки
)4;5;2(
1
M и )0;1;3(
2
−M .
4.
Даны вершины треугольника
)5;2(A
,
)1;3(−B
,
)4;0(C
. Найти уравнение медианы АМ.
5.
Даны координаты вершин пирамиды: )3;2;1(
1
A , )1;2;3(
2
−−A ,
)0;2;4(
3
A
, )1;2;6(
4
−A .
Найти: а) длину ребра
31
AA
;
б) угол между ребрами
31
AA
и
21
AA ;
с) объем пирамиды.
2 вариант
1. Даны вершины треугольника АВС:
)1;5(−A
,
)2;8( −B
,
)4;1(C
. Найти расстояние от
точки
С до прямой АВ.
2.
Записать уравнения прямых, проходящих через точку
)1;1(−A
под углом
o
45
к
прямой
632 =+ yx
.
3.
Написать уравнение плоскости, параллельной плоскости
011635 =+++ zyx
и
проходящей через точку
)8;2;11( −A
.
4.
Составить каноническое уравнение прямой, проходящей через точку
)3;5;1( −M
перпендикулярно к прямым
1
1
3
2
2 −
+
=
−
=
zyx
⎪
⎩
⎪
⎨
⎧
+=
−−=
+=
32
5
13
tz
ty
tx
5.
Найти угол между диагоналями параллелограмма, построенного на векторах
nma += 2 , nmb 2−= , где
2=m
,
3=n
,
(
)
o
60=∠
∧
nm .
3 вариант
1. Найти точку пересечения прямой и плоскости
4
5
1
1
5
7
−
=
−
=
− zyx
0823 =−+− zyx
2.
Составить уравнение плоскости, проходящей через точки
)5;3;2( −M
и
)6;1;1( −−N
параллельно вектору
)3;4;4(=a
.
3.
Записать уравнение прямой в канонической форме
⎩
⎨
⎧
=+++
=++−
0143
0223
zyx
zyx
4.
Доказать, что четырехугольник ABCD – трапеция, если
)6;3(A
,
)2;5(B
,
)3;1( −−C
,
)5;5(−D
.
5.
Даны три вектора:
kjia 32 +−=
,
kjib 23 +−=
,
kjia 423 −+=
. Найти вектор
X
,
удовлетворяющий условиям
()
5−=⋅ ax
,
()
11−=⋅bx
,
()
20=⋅ cx
4 вариант
1. Заданы вершины пирамиды
)0;1;2(A
,
)1;3;1(−B
,
)3;2;0(C
,
)4;2;1( −D
. Найти расстояние от
точки
D до плоскости ABC.
2. Найти уравнение прямой, проходящей через точку
)1;2(−A
параллельно MN, если
)2;3( −−M
,
)6;1(N
.

34
3. Определить, при каком значении С плоскости
0353 =−+− Czyx
и
0523 =++− zyx
будут перпендикулярны.
4. Доказать, что прямая
3
3
1
1
2
1
−
=
−
+
=
+ zyx
параллельна плоскости
02 =−+ zyx
.
5. Даны вершины треугольника
)3;2;3( −A
,
)1;1;5( −B
и
)1;2;1( −C
. Определить его внешний
угол при вершине
А.
5 вариант
1. Доказать, что прямая
3
4
12
2
−
=
−
=
− zyx
лежит в плоскости
02 =−+ zyx
.
2. Составить параметрические уравнения медианы треугольника с вершинами
)7;6;3( −A
,
)4;1;5(−B
,
)3;2;0(C
, проведенной из вершины С.
3. Составить уравнение плоскости, проходящей через точку
)1;3;2( −M
и прямую
3−= tx
,
52 += ty
,
13 +−= tz
.
4. Даны вершины треугольника
АВС:
)3;1( −A
,
)7;0(B
,
)4;2(−C
. Найти уравнение высоты
СH.
5. Векторы
a и b взаимно перпендикулярны, а вектор c образует с ними углы, равные
3
π
. Зная, что
2== ba
и
1=c
, найти
()()
acba −⋅−2
.
6 вариант
1. Написать уравнение плоскости, проходящей через прямую
39
3
2
1 zyx
=
+
=
−
и точку
)2;8;9( −M
. Найти угол между искомой плоскостью и плоскостью
0843 =+−+ zyx
.
2. Найти острый угол между диагоналями параллелограмма, построенного на
векторах
)0;1;2(a
и
)1;1;0( −b
.
3. Найти точку
О, пересечения диагоналей четырехугольника АВСD, если
)3;1( −−A
,
)5;3(B
,
)2;5(C
,
)5;3( −D
.
4. Найти расстояние между плоскостями
01232 =−+− zyx
и
05264 =++− zyx
.
5. Даны координаты вершин пирамиды
АВСD:
)0;0;0(A
,
)0;2;5(B
,
)0;5;2(C
,
)4;2;1(D
.
Найти проекцию вектора
АВ на вектор СD.
7 вариант
1. Даны две вершины треугольника АВС:
)4;4(−A
и
)12;4( −B
и точка
)2;4(M
,
пересечения его высот. Найти вершину
С.
2. Найти угол наклона прямой, проходящей через точки
)3;7;1(
0
−M
и )3;5;2(
1
−M к
плоскости 3
х – 4у +10 = 0.
3. Написать уравнение плоскости, проходящей через точку перпендикулярно к
плоскостям
х + 2у –2z + 4 = 0 и х–2у+ z–4 = 0.
4. Написать уравнения прямой, проходящей через точку
)1;1;2(−M
и параллельно
вектору
)3;2;1( −P
в канонической и параметрической формах.
5. Даны точки
О(0;0;0), А(5;2;0), В(2;5;0), С(1;2;4) вершины пирамиды. Вычислить ее
объем, площадь грани
ABC и высоту пирамиды, опущенную на эту грань
⎟
⎠
⎞
⎜
⎝
⎛
⋅=
Δ 0
3
1
HSV
ABCïèð
.
35
8 вариант
1. Составить канонические уравнения прямой, проходящей через точку
)3;0;1(
4
A
перпендикулярно плоскости, проходящей через точки А
1
(3;0;0), А
2
(0;2;3), А
3
(1;4;1).
2. Найти уравнение плоскости, проходящей через точки
)1;3;1( −A
,
)2;7;4(B
и
перпендикулярной плоскости
021753 =−−+ zyx
.
3. Доказать, что прямая
⎪
⎩
⎪
⎨
⎧
−=
+−=
−=
54
14
23
tz
ty
tx
параллельна плоскости
05634 =−−− zyx
.
4. Даны вершины треугольника
АВС:
)0;7(A
,
)4;1(B
,
)4;8( −−C
. Найти точку пересечения
медианы
AM и высоты СН.
5. Вычислить объем и высоту параллелепипеда, построенного на трех данных
векторах:
{}
2;1;3 −=P
,
{}
3;0;4−=Q
,
{}
5;5;1 −=R
.
9 вариант
1. Найти угол между плоскостью х + у = 0 и плоскостью, проходящей через три точки:
М
1
(1;3;0), М
2
(4;–1;2), М
3
(3
;
0;1).
2. Даны две вершины треугольника
ABC: A(–6;2), В(2;–2) и точка пересечения его
высот
Н(1;2). Найти координаты точки М пересечения стороны АС и высоты ВН.
3. Написать уравнение прямой, проходящей через точку
М
0
(2;–3;–4) параллельно
прямой
⎩
⎨
⎧
=−+−
=+−+
012
02
zyx
zyx
.
4. Показать, что прямые
32
1
1
zyx
=
−
−
=
и
⎩
⎨
⎧
=+−+
=+−+
03632
0153
zyx
zyx
перпендикулярны.
5. Вычислить диагонали и площадь параллелограмма, построенного на векторах
jka −=
и
kjib ++=
.
10 вариант
1. При каком
λ
пересекаются прямые
⎩
⎨
⎧
=+−+
=−−−
04
0532
zyx
zyx
и
2
1
1
33
−
=
+
=
+ zyx
λ
.
2. Найти расстояние от точки
А(–3; 3) до прямой
2
3
2
3
−
=
+ yx
.
3. Составить уравнение плоскости, проходящей через точку
М(–2;7;3) параллельно
плоскости
x – 4y + 5z – l = 0.
4. Даны вершины треугольника
ABC: A(7; 0), В(4; 1), С(–4; –8). Написать уравнение
медианы
ВМ.
5. Даны координаты вершин пирамиды
A
1
(3;1;–2), А
2
(1;–2;1), А
3
(–2;1;0), А
4
(2;2;5).
Найти объем пирамиды и высоту, опущенную из вершины А
3
.
11 вариант
1. Составить канонические уравнения прямой проходящей через начало координат и
параллельно прямой
⎩
⎨
⎧
=+−−
=−
014
04
zy
yx
.
2. Найти угол между прямой
02
3
1
2 zyx
=
−
=
−
и плоскостью
0533 =−−+ zyx
.
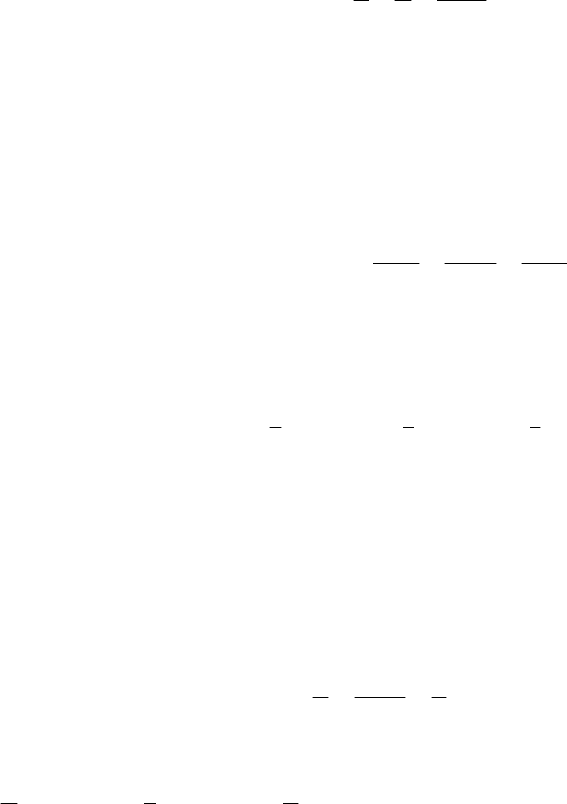
36
3. Составить параметрические уравнения прямой, проходящей через точку А
4
(1;1;0) и
перпендикулярно плоскости
A
1
A
2
A
3
, проходящей через три заданных точки: А
1
(3;0;5);
А
2
(0;0;2), А
3
(4;1;2).
4. Найти расстояние от точки
Р(1;2;3) до прямой
1
2
01 −
−
==
zyx
.
5. Даны вершины треугольника
ABC: A(l;–1;2), В(5;–6;2), С(1;3;1). Вычислить длину
его высоты, опущенной из вершины
В на сторону АС.
12 вариант
1. Определить угол между прямой
⎩
⎨
⎧
=
−=
zx
xy
3
2
и плоскостью х – 2у + z + 4 = 0.
2. Найти расстояние от точки
)3;1;2(
0
−M
до прямой
5
1
4
2
3
1
−
=
+
=
+ zyx
.
3. Составить уравнение плоскости, проходящей через точки
M
1
(–1; 3;2), М
2
(–1;3; –1) и
перпендикулярно к плоскости 3
х + 4у + 12z – 1 = 0.
4. Даны вершины треугольника
АВС: А(–2;–6), В(–3;5), С(4;0). Найти точку
пересечения медианы
АМ и высоты СH.
5. Установить, компланарны ли векторы :
{}
2;1;2 −=a
,
{}
3;2;1 −=b
,
{}
7;4;3 −=c
.
13 вариант
1. Через точку пересечения прямых
0546 =+− yx
и
0852 =++ yx
провести прямую
параллельную оси
Oy.
2. Установить, плоскости
10=−− zyx
;
043114 =++ zx
;
3157 =− yx
имеют единственную
общую точку, и найти ее координаты.
3. Найти угол между прямыми
⎩
⎨
⎧
=+−
=−−
052
02
zx
zyx
и
63
4
2
zyx
=
−
=
.
4. Составить канонические уравнения прямой, проходящей через точку
А
4
(1;1;0)
перпендикулярно плоскости, проходящей через точки
А
1
(3;0;5), А
2
(0;0;2), А
3
(4;1;2).
5. Даны три силы
{}
2;4;3 −=m
,
{}
5;3;2 −=n
,
{}
4;2;3 −−=p
, приложенные к одной точке.
Вычислить, какую работу производит равнодействующая этих сил, когда точка ее
приложения, двигаясь прямолинейно, перемещается из положения
С(5;3;–7) в
положение
В(4;–1;4).
14 вариант
1. Найти угол наклона прямой, проходящей через точки
)2;6;3(
0
−M
и )2;8;7(
1
−−M к
плоскости
05623 =+−− zyx
.
2. Записать уравнения прямой в канонической форме
⎩
⎨
⎧
=++−
=−++
022
02
zyx
zyx
3. Найти уравнение плоскости, проходящей через точки
М
1
(1;1;1) и М
2
(–1;1;–1),
параллельно вектору
АВ, где А(5;–2;3), В(6;1;0).
4. Даны уравнения стороны
АВ треугольника ABC 4х + у = 12, его высот ВН 5х–4у = 12
и
AM х + у = 6. Найти уравнения двух других сторон треугольника ABC.
5. Даны координаты вершин пирамиды
A
1
(l;1;1), А
2
(3 4;0), А
3
(–1:5;6), А
4
(4;0;5).
37
Найти: a) длину ребра А
2
А
3
;
b) угол между ребрами
A
1
A
2
и A
1
A
4
;
c) проекцию вектора
A
1
A
2
на вектор A
1
A
4
.
15 вариант
1. Найти уравнение прямой, проходящей через точку пересечения прямых
0723 =−− yx
,
063 =−+ yx
и отсекающей на оси абсцисс отрезок, равный 3.
2. Даны две точки
А(1;3;–2) и В(7;–4;–4). Через точку В провести плоскость,
перпендикулярную к отрезку
АВ.
3. Составить уравнение плоскости, проходящей через три точки
M(0;0;2), N(3;0;5),
Р(4;1;2).
4. Найти направляющие косинусы прямой и записать уравнения прямой в
каноническом виде
⎩
⎨
⎧
=+−
=−+
02
0
yx
zyx
5. Найти проекции векторов
a ={2;1;3} и b = {l;2; –l} на вектор bac −= 2 .
16 вариант
1. Найти точку пересечения прямой и плоскости и угол между ними
62
1
1
1 zyx
=
+
=
−
,
0132 =+++ zyx
2. Из точки
)2;1;1( −A
провести прямую, перпендикулярную плоскости, проходящей
через точку
)1;3;2( −B
,
)2;0;0(C
,
)5;2;3(−D
.
3. Найти уравнение плоскости, проходящей через точку
)2;2;2(
0
−M
перпендикулярно к
плоскостям
123 −=−− zyx
и
0=−− zyx
.
4. Найти расстояние от точки
А(2;–1) до прямой, проходящей через точку
)0;2(−B
и
точку
)5;3(C
.
5. Определить длины диагоналей параллелограмма, построенного на векторах
nma += 2 и nmb 2−= , где m и n единичные векторы, угол между которыми равен
o
60
.
17 вариант
1. Записать уравнения прямой в канонической форме
⎩
⎨
⎧
=−−−
=+++
0832
024
zyx
zyx
2. Дано
)7;2;2(
1
A , )5;7;7(
2
A ,
)5;3;1(
3
A
, )1;5;1(
4
−A . Написать уравнение перпендикуляра к
плоскости
321
AAA
проходящего через точку
4
A .
3. Определить направляющие косинусы вектора перпендикулярного к плоскости
0922 =−+− zyx
.
4. Даны вершины треугольника
АВС:
)3;3( −−A
,
)7;5( −B
,
)7;7(C
. Написать уравнение
медианы
ВМ.
5. На материальную точку действуют силы
kjif +−= 2
1
,
kjif 22
2
++−=
,
kjif 2
3
−+=
.
Найти работу равнодействующей этих сил при перемещении точки из положения
)0;1;2( −A
в положении
)1;1;4( −B
.

38
18 вариант
1. Доказать, что прямые взаимно перпендикулярны:
⎩
⎨
⎧
=+−−
=+−+
0454
0242
zyx
zyx
,
⎪
⎩
⎪
⎨
⎧
−=
+=
+=
tz
ty
tx
61
32
21
.
2. Определить угол между двумя прямыми:
⎪
⎩
⎪
⎨
⎧
+−=
=
−=
tz
ty
tx
1
2
1
,
3
2
2
1
6
+
=
−
=
zyx
.
3. Из точки
)4;2;3( −M
опустить перпендикуляр на плоскость
01435 =+−+ zyx
.
4. Найти проекцию точки
А(1; 2; 1) на прямую
2
1
13
2
−
=
−
=
− zyx
.
5. Даны координаты вершин параллелепипеда:
А(4;2;–1), В(3;0;4), С(0;0;4), D(5;–1;–3).
Найти объем параллелепипеда и высоту в треугольнике
ABC из точки А.
19 вариант
1. Точка
)2;1;2( −M
является основанием перпендикуляра, опущенного из начала
координат на плоскость. Найти уравнение плоскости.
2. Найти угол между прямой
122 −
==
zyx
и плоскостью, проходящей через точки
)3;0;0(A
,
)7;0;1(−B
,
)0;3;0(C
.
3. Написать уравнения прямой, проходящей через точку
М(2;2;1) параллельно прямой
⎩
⎨
⎧
=+−
=−+
012
02
zx
yx
.
4. Записать уравнение прямой, проходящей через точку
)1;3(A
перпендикулярно к
прямой
ВС, если
)5;2(B
,
)0;1(C
.
5. Проверить, что четыре точки
)1;0;1(
1
A , )6;4;4(
2
A ,
)3;2;2(
3
A
, )7;14;10(
4
A лежат в одной
плоскости.
20 вариант
1. Составить уравнение прямой, проходящей через точку
)1;3;2(M
параллельно прямой
3
2
12
1
−
=
−
=
+ zyx
. Найти расстояние между прямыми.
2. При каких значениях
п и А прямая
6
55
3
+
=
−
=
z
n
yx
перпендикулярна к плоскости
0722 =−−+ zyAx
.
3. Известны уравнения двух сторон ромба
0152 =−− yx
,
03452 =−− yx
и уравнение
одной из его диагоналей
063 =−+ yx
. Найти уравнение второй диагонали.
4. Даны вершины треугольника
ABC: A(4;–3), В(7;3), С(1;10). Записать уравнение
высоты
СH.
5. Найти объем пирамиды с вершинами в точках
А(1;2;–1), B(l;2;l), C(4;l;l), D(–l;3;2).
21 вариант
1. Через точку пересечения прямых
0152 =−− yx
и
074 =−+ yx
провести прямую,
делящую отрезок между точками
)3;4( −A
и
)2;1(−B
в отношении
3
2
=
λ
.

39
2. Найти расстояние от точки А(7;9;7) до прямой
23
1
4
2 zyx
=
−
=
−
.
3. Составить уравнение плоскости, проходящей через точку
)1;3;4( −P
параллельно
прямым
326 −
==
zyx
и
2
4
4
3
5
1
−
=
−
=
+ zyx
.
4. Написать уравнение прямой в каноническом виде и определить направляющие
косинусы
⎩
⎨
⎧
=+−−
=−++
022
01682
zyx
zyx
5. Проверить, лежат ли в одной плоскости точки
)1;0;1(
1
A , )3;2;2(
2
A ,
)12;8;8(
3
A
, )12;14;10(
4
A .
22 вариант
1. Даны уравнения сторон четырехугольника:
0=− yx
,
03 =+ yx
,
04 =−− yx
,
0123 =−+ yx
. Найти уравнения его диагоналей.
2. Составить уравнение плоскости, проходящей через точку
А(1;3;–1) параллельно
прямым
4
5
12
+
=
−
=
zyx
и
3
3
0
3
1
−
=
+
=
zyx
.
3. Найти угол между прямой и плоскостью:
⎩
⎨
⎧
=++
=+−
022
01022
zx
yx
,
034 =−++ zyx
.
4. Составить каноническое уравнение прямой, проходящей через начало координат
параллельно прямой
⎩
⎨
⎧
=+−−
==
014
04
zy
yx
.
5. Даны два вектора
)1;1;0(a
и
)0;1;1(b
. Найти вектор c единично длины
перпендикулярный к вектору
a , образующий угол
4
π
с вектором b и тупой угол с
осью
Oz.
23 вариант
1. Вычислить направляющие косинусы прямой и привести уравнения к
каноническому виду
⎩
⎨
⎧
=+−
=++−
03
021265
zx
zyx
2. Найти расстояние от точки
А(3; 2; 1) до прямой
5
3
32
1
−
==
+ zyx
.
3. Составить уравнение плоскости, проходящей через прямую
2
1
2
4
3
2
−
=
−
+
=
− zyx
,
перпендикулярную плоскости
07323 =−−− zyx
.
4. Найти уравнение прямой, проходящей через точку
)3;2( −A
и точку пересечения
прямых
52 =− yx
и
1=+ yx
.
5. Даны координаты вершин пирамиды
)1;1;1(
1
A , )1;4;3(
2
A ,
)2;3;1(
3
−A
, )5;0;4(
4
−A .
Найти: а) длину ребра
32
AA
;
b) объем пирамиды;
с) высоту из вершины
1
A .
40
24 вариант
1. Даны уравнения высот треугольника ABC
0132 =+− yx
,
012 =++ yx
и координаты
его вершин
)3;2(A
. Найти уравнение сторон АВ и АС треугольника.
2. Написать канонические уравнение прямой, проходящей через точки
)4;1;3(
1
−M и
)2;1;1(
2
M .
3. Найти угол между прямыми:
⎪
⎩
⎪
⎨
⎧
+=
−=
+=
52
26
13
tz
ty
tx
,
⎩
⎨
⎧
+=
−=
13
629
zx
yx
.
4. Написать уравнение плоскости, которая проходит через точку
М(3; 1;–2) и прямую
12
3
5
4 zyx
=
+
=
−
.
5. Вычислить
()()
[
]
ACABACAB −×− 243
, если
)2;4;3(A
,
)1;5;3( −B
,
)5;3;2(C
.
25 вариант
1. Определить угол между прямой и плоскостью
⎩
⎨
⎧
=
=
zy
xz
2
,
22 =−+ zyx
2. Составить канонические уравнения прямой, проходящей через точку
А
4
(2;–2;1)
перпендикулярно плоскости, проходящей через точки
A
1
(l;0;–4), А
2
(–2;2;3), А
3
(3;–1;1).
3. Найти уравнение плоскости, проходящей через параллельные прямые
3
2
2
1
1
1
−
=
−
+
=
− zyx
и
3
2
2
1
1
+
=
−
−
=
zyx
4. Дан треугольник с вершинами
)1;3(A
,
)1;3( −−B
,
)12;5( −C
. Найти уравнение и
вычислить длину его медианы, проведенной из вершины
С.
5. Построить треугольник с вершинами
А(1;–2;8), В(0;0;4), С(6;2;0). Вычислить его
площадь и высоту
BD.
26 вариант
1. Вычислить координаты точки пересечения перпендикуляров, проведенных через
середины сторон треугольника, вершинами которого служат точки
)3;2(A
,
)3;0( −B
,
)3;6( −C
.
2. Проверить, параллельны ли прямая и плоскость
⎩
⎨
⎧
=−−
=+−
024
0113
zy
yx
,
015 =+−+ zyx
.
3. Написать уравнение плоскости, проходящей через две параллельные прямые
021
zyx
=
−
=
,
0
1
2
2
1
1
+
=
−
−
=
− zyx
.
4. Написать уравнения прямой в канонической форме
⎩
⎨
⎧
=−−+
=−+−
0745
0132
zyx
zyx
.
5. Доказать, что векторы
kjia 4++=
,
jib 2−=
,
kjic 433 +−=
компланарны.
