Гуменникова Ю.В., Лаврусь О.Е., Хайруллина Р.Н. (сост.) Методические указания и контрольные задания по предмету Аналитическая геометрия для студентов первых курсов всех специальностей очной формы обучения
Подождите немного. Документ загружается.


21
0
1
1
3
4
2 +
=
−
=
−
− zyx
. Заметим, что последнее выражение
0
1+z
следует рассматривать как
уравнение
01 =+z
или
1−=z
. Получаем частный случай расположения прямой в
пространстве – данная прямая параллельна координатной плоскости
Оxy (лежит в
плоскости
1−=
z
и описывается следующим уравнением
1
3
4
2 −
=
−
− yx
;
)3(4)2( −−=− yx
или
0144 =−+ yx
.
Запишем параметрические уравнения этой прямой:
⎪
⎭
⎪
⎬
⎫
−=
+=
−=
.1
,3
,42
z
ty
tx
при
2=t
получаем т.
)1;5;6(
3
−−M
,
при
1−=t
получаем т. )1;2;6(
4
−M .
3) Находим направляющий вектор
s прямой, заданной общими уравнениями
⎭
⎬
⎫
=−+−
=+−+
042
,032
yx
zyx
,
где
)1;1;2(
1
−n
,
)0;2;1(
2
−n
.
kji
kji
nns 52
021
112
21
++=
−
−=×=
, т.е.
)5;1;2(s
Найдем теперь координаты любой точки этой прямой. Т.к. уравнений в системе два, а
переменных три, одну из них задаем произвольно, например
0=x
, получаем
)5;2;0(2 ,5
042
,03
0
Myz
y
zy
⇒==⇒
⎭
⎬
⎫
=−
=+−
.
Составим канонические уравнения:
⎪
⎭
⎪
⎬
⎫
+=
+=
=
.55
,2
,2
tz
ty
tx
при
1=t
получаем т. )10;3;2(
1
M ,
при
1−=t
получаем т. )0;1;2(
2
−M .
Задание 5
Даны точки )3;2;1(
1
A , )0;1;2(
2
−A ,
)1;3;4(
3
−A
и )3;2;2(
4
−A . Составить уравнения:
1) прямой
21
AA ;
2) прямой
NA
3
, параллельной прямой
21
AA ;
3) прямой
MA
4
, перпендикулярной плоскости
321
AAA
;
4) вычислить косинус угла между прямыми
21
AA и
41
AA ;
5) вычислить синус угла между прямой
41
AA и плоскостью
321
AAA
. Найти координаты
точки пересечения этой прямой и плоскости;
6) найти расстояние от т.
4
A до прямой
21
AA .
22
Решение:
1) уравнение прямой
21
AA составим по формуле (2.4)
3
3
3
2
1
1
−
−
=
−
−
=
− zyx
.
2) уравнение прямой
NA
3
, параллельной прямой
21
AA составим по формулам (2.2) и (2.3),
учитывая что ее направляющий вектор
)3;3;1(
21
−−== AAs
:
канонические:
3
1
3
3
1
4
−
−
=
−
+
=
− zyx
,
параметрические:
⎪
⎭
⎪
⎬
⎫
−=
−−=
+=
.31
,33
,4
tz
ty
tx
3) составим сначала уравнение плоскости
321
AAA
по формуле (1.4):
0
253
331
321
=
−−
−−
−−− zyx
или
011479 =−−+ zyx
Нормальный вектор этой плоскости
)4;7;9( −n
является направляющим s для прямой MA
4
,
ее канонические уравнения составим по формуле (2.3):
4
3
7
2
9
2
−
+
=
−
=
− zyx
.
4) косинус угла между прямыми
21
AA :
3
3
3
2
1
1
−
−
=
−
−
=
− zyx
и
41
AA :
6
3
0
2
1
1
−
−
=
−
=
− zyx
вычислим как косинус угла между их направляющими векторами
)3;3;1(
1
−−s
и
)6;0;1(
2
−s
по
формуле (2.5):
(
)
72,0
3719
19
)6(01)3()3(1
)6()3(0)3(11
coscos
222222
2
,
1
≈
⋅
=
−++⋅−+−+
−⋅−+⋅−+⋅
==
∧
ss
ϕ
.
5) Угол между прямой
41
AA :
6
3
0
2
1
1
−
−
=
−
=
− zyx
и плоскостью
321
AAA
:
011479 =−−+ zyx
вычислим через угол между векторами
)6;0;1( −s
и
)4;7;9( −n
по формуле (2.8):
(
)
45,0
14637
33
164981361
)4()6(7091
cossin
,
≈
⋅
=
++⋅+
−⋅−+⋅+⋅
==
∧
sn
ϕ
.
Для вычисления координат точки пересечения прямой
41
AA и плоскости
321
AAA
воспользуемся формулой (2.7):
0
)6()4(0719
113)4(2719
=
−⋅−+⋅+⋅
−⋅−+⋅+⋅
−=t
В параметрические уравнения прямой
41
AA
⎪
⎭
⎪
⎬
⎫
−=
=
+=
.63
,2
,1
tz
y
tx
подставляем
0=t
, получаем координаты точки пересечения
)3;2;1(
, что и так
понятно из задания.
23
6) расстояние от т. )3;2;2(
4
−A до прямой
21
AA :
3
3
3
2
1
1
−
−
=
−
−
=
− zyx
найдем по формуле (2.6):
s
MMs
h
10
×
=
,
)3;3;1( −−s
,
)6;0;1(
4110
−= AAMM
,
kji
kji
AAsMMs 3318
601
331
4110
++=
−
−−=×=×
,
3423318
222
10
=++=× MMs ,
19)3()3(1
222
=−+−+=s ,
24,4
19
342
≈=h
ед.
Задание 6. Найти координаты точки );;(
2222
zyxM симметричной точке )0;2;4(
1
−M
относительно плоскости
01432 =+−+ zyx
Решение:
Запишем параметрические уравнения прямой
21
MM , перпендикулярной данной
плоскости, т.е. вектор, нормальный для плоскости
)3;2;1( −n
является направляющим для
прямой
21
MM :
⎪
⎭
⎪
⎬
⎫
−=
+−=
+=
.30
,22
,4
tz
ty
tx
Подставляя их в уравнение плоскости, находим
t :
014)3(3)22(2)4( =+−−+−++ ttt
, откуда
1−=t
и, следовательно, точка М пересечения прямой
21
MM с данной плоскостью
)3;4;3( −M
. Т.к. т. М является серединой отрезка
21
MM , то
верны равенства:
2
4
3
2
x+
=
;
2
2
4
2
y+−
=−
;
2
0
3
2
z+
=
, из которых находим координаты точки
2
M : 2
2
=x ; 6
2
−=y ;
6
2
=z .
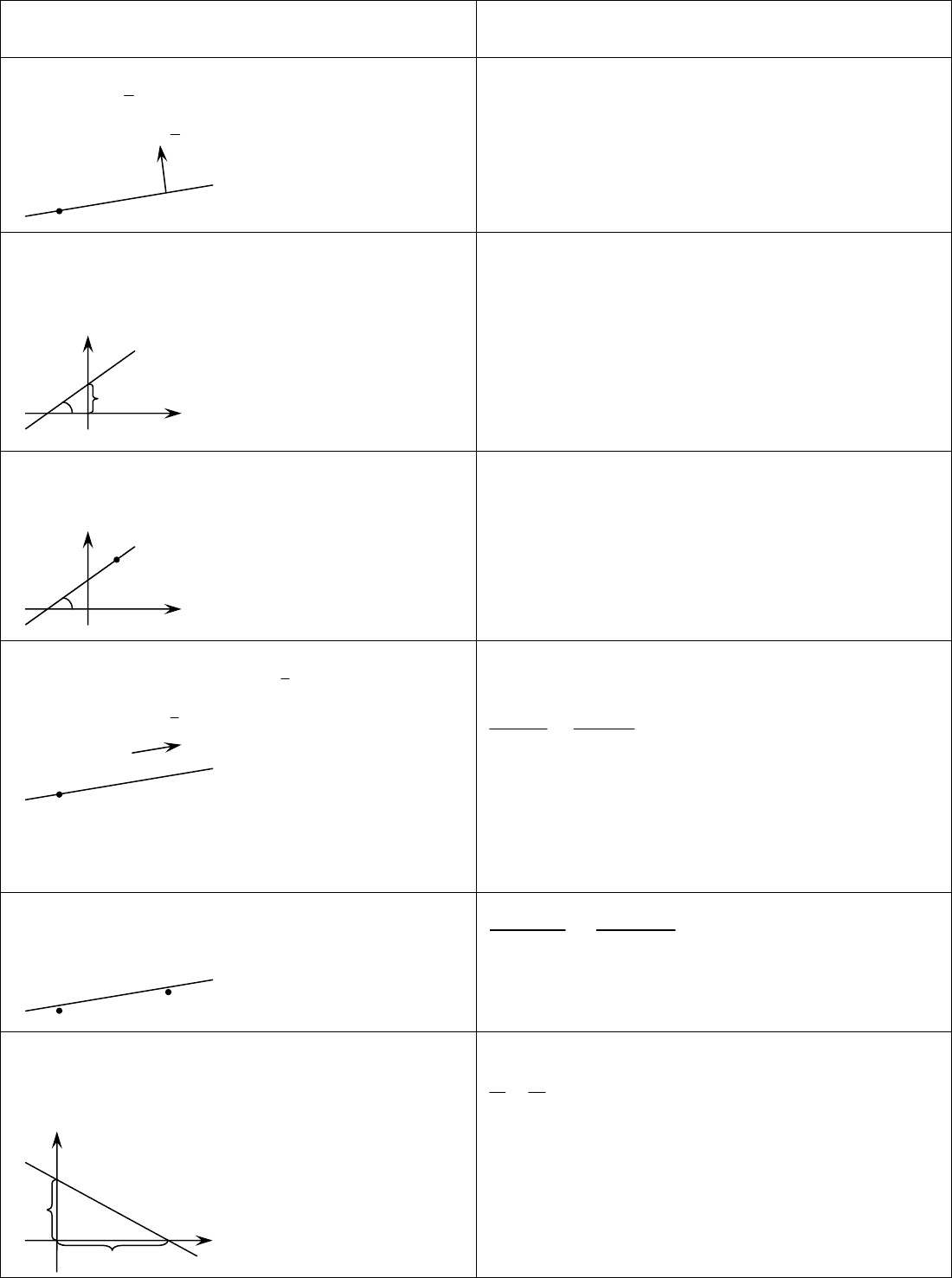
3. Прямая на плоскости
Определение. Совокупность точек плоскости, координаты которых
);( yx
удовлетворяют уравнению
0=++ CByAx
(3.1)
называется
прямой на плоскости.
где
А, В, С
∈
R, причем
0
22
>+ BA
Уравнение (3.1) называется
общим уравнением прямой, коэффициенты А, В
являются координатами вектора
n , перпендикулярного к данной прямой.
В зависимости от способа задания прямой на плоскости существует несколько
видов ее уравнений (см. таблицу).
24
Таблица 3
Способ задания прямой и заданные
параметры
Вид уравнения прямой и его название
1. Прямая задана точкой
);(
000
yxM
и
нормалью
);( BAn
0)()(
00
=−+− yyBxxA
(3.2)
2. Прямая задана угловым коэффициентом
k
(
α
tgk =
) и отрезком «
b
», отсекаемым ей
на оси
Оy
Уравнение прямой с угловым
коэффициентом
bkxy +=
(3.3)
3. Прямая задана точкой
);(
000
yxM
и
угловым коэффициентом
α
tgk =
)(
00
xxkyy −=−
(3.4)
4. Прямая задана точкой
);(
000
yxM
и
направляющим вектором
),( nms
а) Каноническим уравнением прямой на
плоскости
n
yy
m
xx
00
−
=
−
(3.5)
б) Параметрические уравнения прямой на
плоскости
⎭
⎬
⎫
+=
+=
.
,
0
0
ntyy
mtxx
t – параметр (3.6)
5. Прямая задана 2-мя точками );(
111
yxM и
);(
222
yxM
12
1
12
1
yy
yy
xx
xx
−
−
=
−
−
(3.7)
6. Прямая задана отрезками
a
и
b
,
отсекаемыми ей на осях координат
Ох и Оy
соответственно
Уравнение прямой «в отрезках»
1=+
b
y
a
x
(3.8)
y
х
b
a
1
M
2
M
0
M
s
y
x
0
α
0
M
0
M
n
y
x
b
0
α

25
Замечание! Уравнение (3.2) – (3.8) приводятся к виду (3.1)
Основные задачи.
1.
Угол между прямыми на плоскости
а) прямые заданы общими уравнениями
0
111
=++ CyBxA и 0
222
=++ CyBxA , тогда
2
2
2
2
2
1
2
1
2121
21
21
cos
BABA
BBAA
nn
nn
+⋅+
+
=
⋅
⋅
=
ϕ
(3.9)
условие параллельности прямых:
2
1
2
1
2
1
C
C
B
B
A
A
≠=
;
Условие перпендикулярности:
0
2121
=+ BBAA .
б) прямые заданы уравнениями с угловыми коэффициентами
11
bxky += и
22
bxky +=
21
12
1 kk
kk
tg
+
−
=
ϕ
(3.10)
Условие параллельности прямых:
21
kk = ;
условие перпендикулярности:
1
21
−=kk
2.
Расстояние d от точки
);(
000
yxM
до прямой
0=++ CByAx
вычисляется по
формуле:
22
00
BA
CByAx
d
+
++
=
(3.11)
Задание 7
Написать общее уравнение и построить прямые, проходящие через т.
);(
00
yxМ
параллельно:
1)
оси Ох;
2)
оси Оy;
3)
биссектрисе первого координатного угла;
4)
биссектрисе второго координатного угла;
5)
прямой
0=++ CByAx
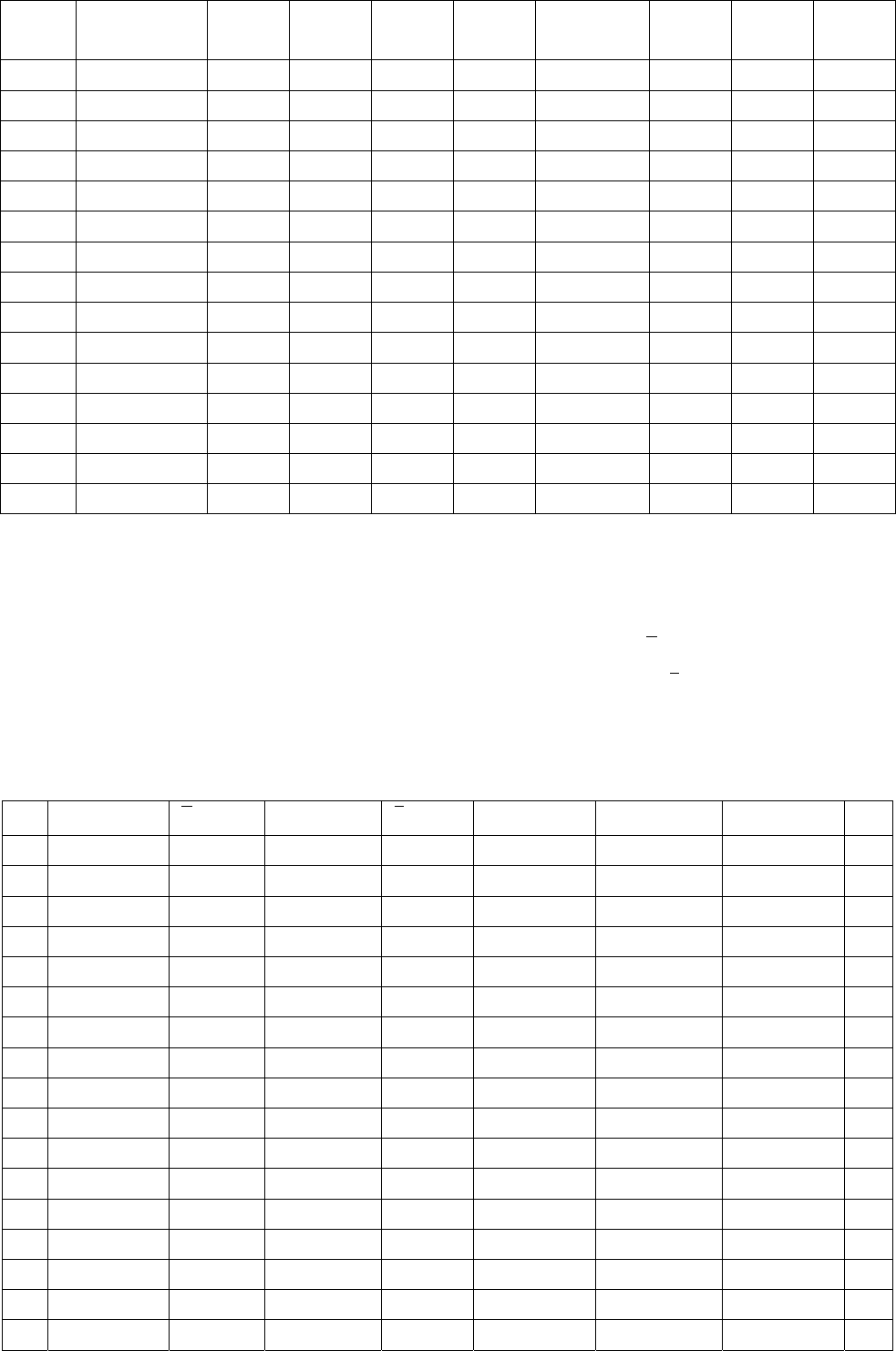
26
№
вар.
);(
00
yxМ
А В С
№
вар.
);(
00
yxМ
А В С
1
(2; –1) 2 –3 1
2
(3; –2)
4 2 –1
3
(–1;5) –2 1 3
4
(–2, 5)
3 –1 1
5
(4, 9) –5 –3 1
6
(–3, 1)
1 1 1
7
(4, 5)
–1 –6 3
8
(4, –1)
2 –1 –3
9
(4, –5)
4 –5 0
10
(–5, 3)
1 1 1
11
(4, 4)
–1 1 1
12
(0, –6)
2 1 –3
13
(4, 6)
2 1 3
14
(–2, –3)
1 1 1
15
(3, 5)
3 –4 3
16
(–6, 2)
3 –1 0
17
(10, 6)
1 1 2
18
(1, 5)
2 –1 1
19
(1, 8)
–3 –5 3
20
(5, –2)
4 3 –9
21
(6, 5)
3 –5 1
22
(5, –2)
3 2 1
23
(7, 2)
3 1 2
24
(9, 6)
1 –2 3
25
(8, 4)
3 –4 3
26
(7, 5)
4 –3 2
27
(2, 3)
5 –3 5
28
(4, 7)
1 1 2
29
(4, 0)
–1 2 4
30
(7, 3)
2 –1 –1
Задание 8
Записать общее уравнение и построить прямые, найти их угловые коэффициенты:
1)
прямая задана точкой
);(
000
yxM
и нормальным вектором
);( BAn
;
2)
прямая задана точкой );(
111
yxM и направляющим вектором
),( nms
;
3)
прямая задана двумя точками
);(
332
yxM
и
);(
443
yxM
;
4)
прямая задана точкой
);(
554
yxM
и угловым коэффициентом
k
№
);(
000
yxM
);( BAn
);(
111
yxM
),( nms
);(
222
yxM
);(
333
yxM
);(
444
yxM
k
1
(1,2) (–3,1) (2,–1) (3,–4) (–5,0) (2, –3) (4,-1) 3
2
(2,–3) (0,4) (3,1) (–2,5) (0,–3) (4,0) (5,1) –2
3
(3, 2) (1, 1) (8, 4) (4, 5) (6, 5) (3, 2)
(6, 9)
6
4
(0, 6) (7, 2) (–2, 4) (5, 7) (4, 0) (6, 8)
(2, 3)
–1
5
(2, 4) (6, 4) (5, 2) (5, 5) (1, 2) (5, 7)
(8, 7)
2
6
(3, 2) (4, 6)
(–2, –3) (–3, 1)
(3, 0)
(0, 4)
(1, –1)
4
7
(–2, 1) (5, 3)
(–1, 2) (4, –1)
(7, 10) (5, –4)
(1, –1)
–3
8
(4, 0) (5, 6)
(1, 2,) (3, 2)
(6, 9) (4, 0)
(–2, 0)
5
9
(4, 10)
(3, 5)
(–2, –4) (0, 4) (–2, 5)
(3, 0)
(3, 2)
2
10
(6, 9) (1, 2) (1, –1)
(4, 5) (3, 4) (6, 6)
(6, 6)
3
11
(1,1) (–1,4) (2,6)
(–2,–1)
(3, 2) (1, 3) (–2, 2)
–3
12
(0, 5) (2, 3) (0, 0)
(–3, 1)
(1, 3) (3, 2) (4, 0)
–6
13
(0, 0) (4, 0) (1, 3)
(4, –1)
(3, 1) (1, –2) (2, 2)
–5
14
(2, –5) (3, 2) (5, –3)
(–5, 3)
(–2, 1) (2, 2) (3, 1)
1
15
(6, 0) (0, 6) (4, 6)
(0, –6)
(2, 2) (–2, 1) (1, –2)
1
16
(3, 2) (2, 4) (4, 3)
(–2, 4)
(1, –1) (5, –2) (–1, 3)
–4
17
(6, 3) (5, –4) (3, 5)
(–6, 2)
(6, 15) (3, 0) (4, 5)
1

27
№
18
(5, –2) (4, 0) (2, 5)
(1, 2)
(1, –2) (1, –2) (2, 2)
–5
19
(4, 2) (3, 0) (0, 3)
(5, –2)
(4, 0) (1, 2) (1, 3)
–5
20
(4, 2) (3, 0) (0, 2)
(5, –2)
(–5, 6) (–5, 2) (6, 5)
1
21
(4, 4) (7, 10) (2, 8)
(9, 6)
(6, 6) (8, 4) (8, 9)
–4
22
(4, 6) (6, 9) (2, 10)
(7, 5)
(8, 2) (2, 6) (7, 4)
–3
23
(3, 5) (8, 7) (5, 10)
(4, 7)
(6, 5) (9, 5) (6, 11)
2
24
(10, 6) (–2, 8) (6, 8)
(7, 10)
(2, 2) (7, 7) (3, 1)
–2
25
(1, 8) (5, 2) (5, 7)
(4, 10)
(6, 4) (5, 5) (6, 8)
–3
26
(6, 6) (4, 9) (4, 6)
(6, 9)
(7, 3) (5, 8) (5, 8)
–6
27
(7, 2) (5, 7) (5, 3)
(2, 3)
(1, 2) (0, 0) (2, 7)
1
28
(8, 6) (10, 5) (5, 6)
(8, 10)
(2, 7) (3, 2) (1, 2)
–1
29
(7, 7) (6, 5) (3, 5)
(8, 4)
(3, 2) (2, 7) (0, 0)
2
30
(–2, 1) (4, 0) (3, 2)
(1, 3)
(1, –2) (–2, 1) (2, 5)
3
Задание 9
Даны вершины треугольника
ABC
: ),(
11
yxA , ),(
22
yxB ,
),(
33
yxC
. Построить треугольник и
найти:
1)
уравнения сторон
A
B и
AC
;
2)
уравнение высоты
CH
;
3)
уравнение медианы
AM
;
4)
точку
N
пересечения медианы
A
M и высоты
CH
;
5)
уравнение прямой, проходящей через вершину
C
параллельно стороне
A
B ;
6)
угол
ABC
;
7)
длину высоты
CH
.
№ вар.
),(
11
yxA ),(
22
yxB
),(
33
yxC
№ вар.
),(
11
yxA ),(
22
yxB
),(
33
yxC
1
(–2;4) (3;1) (10;7)
2
(–3; –2) (14;4) (6;8)
3
(1;7) (–3; –1) (11; –3)
4
(1;0) (–1;4) (9;5)
5
(1; –2) (7;1) (3;7)
6
(–2; –3) (1;6) (6;1)
7
(–4;2) (–6;6) (6;2)
8
(4; –3) (7;3) (1;10)
9
(4; –4) (8;2) (3;8)
10
(–3; –3) (5; –7) (7;7)
11
(1; –6) (3;4) (–3;3)
12
(–4;2) (8; –6) (2;6)
13
(–5;2) (0; –4) (5;7)
14
(4; –4) (6;2) (–1;8)
15
(–3;8) (–6;2) (0; –5)
16
(6; –9) (10; –1) (–4;1)
17
(4;1) (–3; –1) (7; –3)
18
(–4;2) (6; –4) (4;10)
19
(3; –1) (11;3) (–6;2)
20
(–7; –2) (–7;4) (5; –5)
21
(–1; –4) (9;6) (–5;4)
22
(10; –2) (4; –5) (–3;1)
23
(–3; –1) (–4; –5) (8;1)
24
(–2; –6) (–3;5) (4;0)
25
(–7; –2) (3; –8) (–4;6)
26
(0;2) (–7; –4) (3;2)
27
(7;0) (1;4) (–8; –4)
28
(1; –3) (0;7) (–2;4)
29
(–5;1) (8; –2) (1;4)
30
(2;5) (–3;1) (0;4)
);(
000
yxM
);( BAn
);(
111
yxM
),( nms
);(
222
yxM
);(
333
yxM
);(
444
yxM
k
28
Задание 10
Решить следующие задачи.
1 вариант. Найти уравнение прямой, проходящей через точку пересечения прямых
0723 =−− yx
и
063 =−+ yx
отсекающей на оси абсцисс отрезок, равный 3.
2 вариант. Найти проекцию точки А (–8,12) на прямую, проходящую через точки В (2,–3)
и
С(–5,1).
3 вариант. Даны две вершины треугольника ABC: A (–4,4), В(4, –12) и точка М(4,2)
пересечения его высот. Найти вершину
С.
4 вариант. Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и
проходящей параллельно прямой
32 =− xy
.
5 вариант. Найти уравнение прямой, проходящей через точку А(2,–3) и точку
пересечения прямых
52 =− yx
и
1=+ yx
.
6 вариант. Доказать, что четырехугольник A B C D – трапеция, если А(3, 6), В(5, 2),
С(–1,–3), D(–5,5).
7 вариант. Записать уравнение прямой, проходящей через точку А(3,1) перпендикулярно
к прямой
ВС, если В(2,5), С(1,0).
8 вариант. Найти уравнение прямой, проходящей через точку А(–2,1) параллельно
прямой
MN, если М(–3, –2), N(1,6).
9 вариант. Найти точку, симметричную точке М(2,–1) относительно прямой
032 =+− yx
.
10 вариант. Найти точку О пересечения диагоналей четырехугольника ABCD, если
А(–1, –3), В(3,5), С(5,2), D(3, –5).
11 вариант. Через точку пересечения прямых
0546 =+− yx
,
0852 =++ yx
провести
прямую, параллельную оси абсцисс.
12 вариант. Известны уравнения стороны АВ треугольника ABC
124 =+ yx
, его высот ВН
1245 =− yx
АМ
6=+ yx
. Найти уравнения двух других сторон треугольника ABC.
13 вариант. Даны две вершины треугольника ABC A(–6,2), В(2,–2) и точка пересечения
его высот
H(1,2). Найти координаты точки М пересечения стороны АС и высоты ВН.
14 вариант.
Найти уравнения высот треугольника ABC, проходящих через вершины А и
В,
если А(–4,2), B(3, –5), С(5,0).
15 вариант.
Вычислить координаты точки пересечения перпендикуляров, проведенных
через середины сторон треугольника, вершинами которого служат точки
А(2,3), В(0,–3),
С(6, –3).
16 вариант.
Составить уравнение высоты, проведенной через вершину А треугольника
ABC, зная уравнения его сторон:
032 =−− yx
(АВ),
075 =−+ yx
(АС),
01323 =+− yx
(ВС).
17 вариант.
Дан треугольник с вершинами А(3,1), В(–3, –1) и С(5,–12). Найти уравнение
медианы, проведенной из вершины
С, и вычислить ее длину.
18 вариант.
Составить уравнение прямой, проходящей через начало координат и точку
пересечения прямых
0852 =−+ yx
и
0432 =++ yx
.
19 вариант. Найти уравнения перпендикуляров к прямой
01553 =−+ yx
, проведенных
через точки пересечения данной прямой с осями координат.
20 вариант.
Даны уравнения сторон четырехугольника:
0=− yx
,
03 =+ yx
,
04 =−− yx
,
0123 =−+ yx
. Найти уравнения его диагоналей.

29
21 вариант. Составить, уравнения медианы СМ и высоты СК треугольника ABC, если
А(4,6), В(–4,0), С(–1,–4).
22 вариант.
Через точку Р(5, 2) провести прямую: а) отсекающую равные отрезки на
осях координат; б) параллельную оси
Ох; в) параллельную оси Оу.
23 вариант.
Записать уравнение прямой, проходящей через точку А(–2,3) и
составляющей с осью
Ох угол: а) 45°; б) 90°; в) 0°.
24 вариант. Какую ординату имеет точка С, лежащая на одной прямой с точками
А(–6,–6) и В(–3, –1)и имеющая абсциссу, равную 3?
25 вариант.
Через точку пересечения прямых
0152 =−− yx
и
074 =−+ yx
провести
прямую, делящую отрезок между точками
А(4 –3) и В(–1,2) в отношении
λ
=2/3.
26 вариант.
Известны уравнения двух сторон ромба
0152 =−− yx
и
03452 =−− yx
и
уравнение одной из его диагоналей
063 =−+ yx
. Найти уравнение второй диагонали.
27 вариант.
Найти точку Е пересечения медиан треугольника, вершинами которого
являются точки
А(–3,1), В(7,5) и С(5, –3).
28 вариант.
Записать уравнения прямых, проходящих через точку А(–1,1) под углом 45°
к прямой
632 =+ yx
.
29 вариант.
Даны уравнения высот треугольника ABC
0132 =+− yx
,
012 =++ yx
и
координаты его вершины
А(2,3). Найти уравнения сторон АВ и АС треугольника.
29 вариант.
Даны уравнения двух сторон параллелограмма
02 =− yx
,
01 =−− yx
и точка
пересечения его диагоналей
М(3,–1). Найти уравнения двух других сторон.
Решение типового варианта
Задание 7.
Написать общее уравнение и построить прямые, проходящие через т.
)1;3( −М
параллельно:
1)
оси Ох;
2)
оси Оy;
3)
биссектрисе первого координатного угла;
4)
биссектрисе второго координатного угла;
5) прямой
042 =+− yx
.
Решение:
1) Т.к. прямая параллельна оси
Ох, то в уравнении (3.2)
0=A
,
получаем
0)1( =−yB
,
01 =+y
или окончательно,
1−=y
.
2) Т.к. прямая параллельна оси
Оy, то
0=B
, т.е.
0)3( =−xA
⇒
3=x
.
3) У биссектрисы 1-го координатного угла угловой коэффициент
1
0
=k
(т.к.
145 =
o
tg
). Поскольку искомая прямая параллельна
биссектрисе 1-го угла, то ее угловой коэффициент также равен 1.
по формуле (3.4) получаем:
)3(11 −=+ xy
откуда окончательно имеем
04 =−− yx
.
y
x
3=x
1−=y
1
1 0
А
М
1
1
0
А
х
y
04 =−− yx
02 =−+ yx
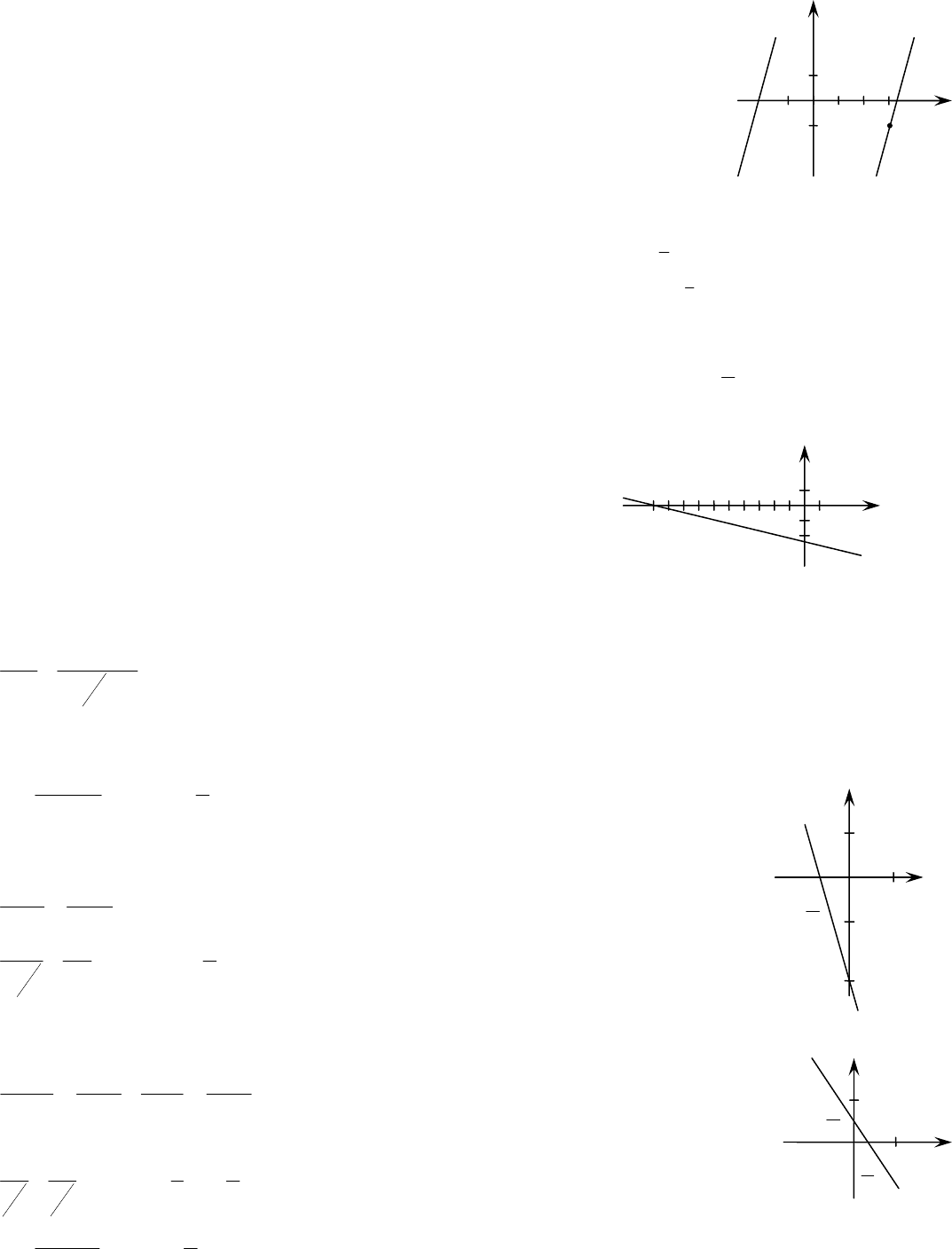
30
4) У биссектрисы 2-го координатного угла
1
0
−=k
, получаем
)3(11 −−=+ xy
, окончательно
02 =−+ yx
.
5) Найдем угловой коэффициент
k
прямой
042 =+− yx
, для чего
приведем ее общее уравнение к виду (3.3)
42 += xy
⇒
2=k
По формуле (3.4) получаем уравнение искомой прямой:
)3(21 −=+ xy
, откуда
072 =−− yx
.
Задание 8.
Записать общее уравнение и построить прямые, найти их угловые коэффициенты:
1)
прямая задана точкой
)3;2(
0
−M
и нормальным вектором
)4;1(n
;
2)
прямая задана точкой )2;0(
1
−M и направляющим вектором
)3;1(−s
;
3)
прямая задана двумя точками )2;1(
2
−M и
)5;0(
3
M
;
4)
прямая задана точкой )3;2(
4
−M и угловым коэффициентом
2
3
=k
.
Решение.
1) По формуле (3.2) получаем
0)3(4)2(1 =++− yx
;
0104 =++ yx
– общее уравнение прямой.
Для построения прямой ее общее уравнение переводят в
уравнение «в отрезках» (3.8):
104 −=+ yx
;
1
4
10
10
=
−
+
−
yx
⇒
10−=a
,
5,2−=b
.
Для определения углового коэффициента
k
данной прямой ее общее уравнение приводят
к виду (3.3):
4
10
−−
=
x
y
⇒
4
1
−=k
.
2) по формуле (3.5) получаем:
023
3
2
1
0
=++⇒
+
=
−
−
yx
yx
– общее уравнение прямой.
;2;
3
2
,1
2
3
2
−=−=
⇒=
−
+
−
ba
yx
3,23 −=⇒−−= kxy
.
3) по формуле (3.7) для прямой
32
MM
получаем:
42
4
31
3
+
+
=
−−
−
yx
;
6
4
4
3
+
=
−
− yx
;
0123 =−+ yx
- общее уравнение прямой.
2
1
;
3
1
1
2
1
3
1
==
⇒=+ ba
yx
;
2
3
,
2
13
−=⇒
+−
= k
x
y
.
1
1
0
х
y
042 =+− yx
072 =−− yx
-10
-2,5
1
1
y
x
y
x
1
1
-2
3
2
−
y
x
1
1
3
1
2
1
