Гуменникова Ю.В., Лаврусь О.Е., Хайруллина Р.Н. (сост.) Методические указания и контрольные задания по предмету Аналитическая геометрия для студентов первых курсов всех специальностей очной формы обучения
Подождите немного. Документ загружается.

41
II. Линии и поверхности второго порядка
Определение. Линией (кривой) второго порядка называется совокупность точек
плоскости, декартовы координаты
),( yx
которых удовлетворяют алгебраическому
уравнению второй степени.
022
021
2
2212
2
11
=+++++ ayaxayaxyaxa
(1.1)
где
constaaaaaa =
021221211
,,,,,
.
Определение. Поверхностью второго порядка называется множество точек
пространства, декартовы координаты которых
),,( zyx
удовлетворяют алгебраическому
уравнению второй степени
0222222
0321231312
2
33
2
22
2
11
=+++++++++ azayaxayzaxzaxyazayaxa
(1.2)
где
constaaa =
02211
,...,,
.
Уравнение (1.1) и (1.2) называется
общими уравнениями линии и поверхности
второго порядка
соответственно. Рассмотрим частные случаи этих уравнений.
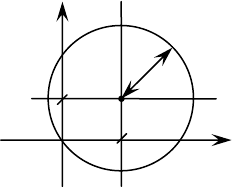
1. Окружность и сфера
Определение. Совокупность точек плоскости, равноудаленных от данной точки
1
O
(центра окружности), называется
окружностью.
Окружность с центром в т.
)0;0(O
и радиусом
R
задается уравнением (каноническим)
222
Ryx =+
. (1.3)
Окружность с центром в т.
),(
001
yxO
и радиусом
R
(на
рисунке) задается уравнением
22
0
2
0
)()( Ryyxx =−+−
. (1.4)
В пространстве окружности соответствует
сфера.
Каноническое уравнение сферы:
2222
Rzyx =++
. (1.5)
Если же центр сферы находится в т.
),,(
0001
zyxO
то уравнение ее имеет вид:
22
0
2
0
2
0
)()()( Rzzyyxx =−+−+−
(1.6)
2. Эллипс и эллипсоид
Определении. Эллипсом называется совокупность точек М плоскости, сумма
расстояний от каждой из которых до двух данных точек (фокусов эллипса) есть величина
постоянная, т.е.
aconstMFMF 2
21
==+ .
y
х
R
0
x
0
y
42
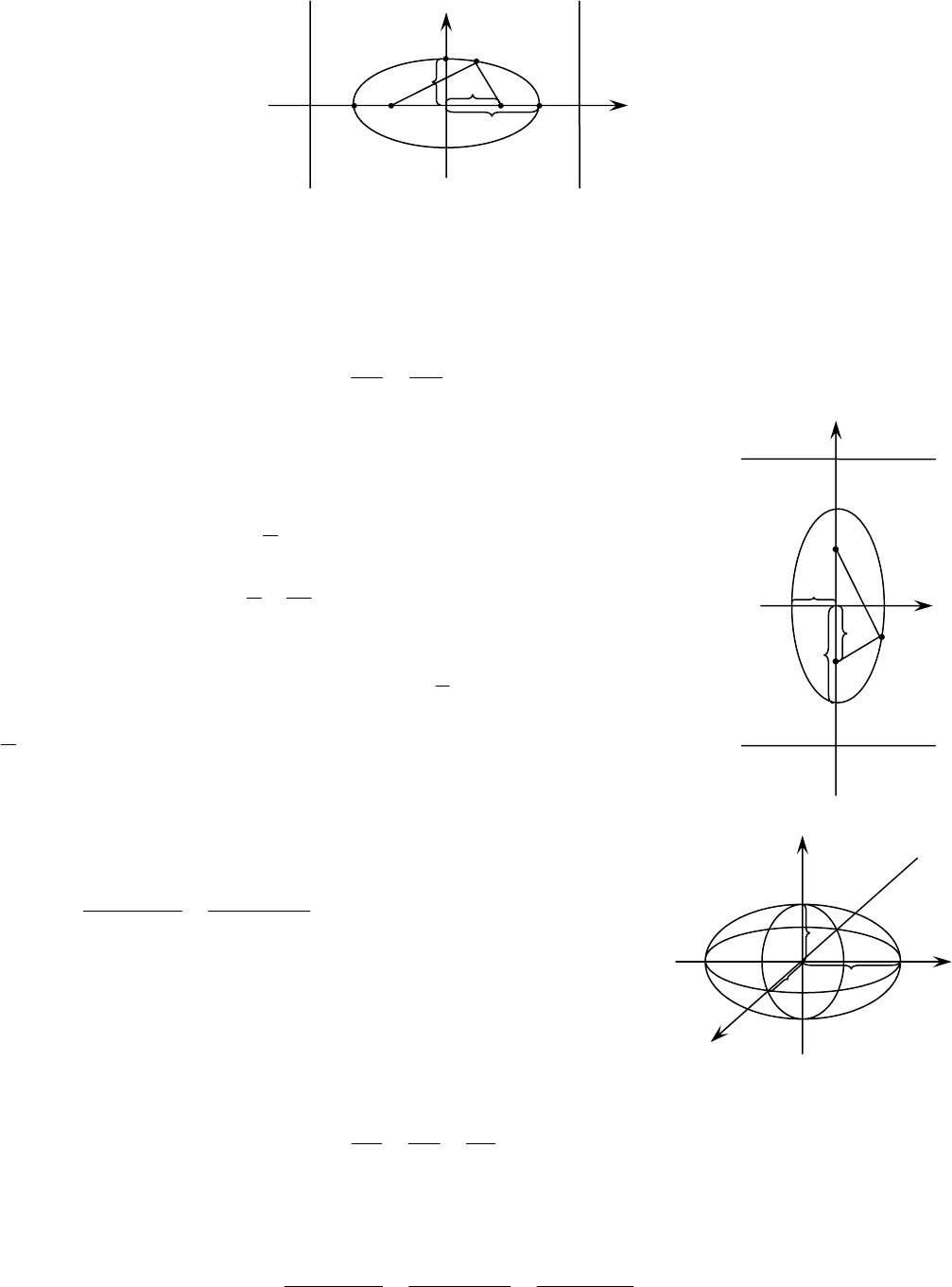
Здесь т.
21
, FF – фокусы эллипса;
aOA =
– большая полуось,
bOB =
– малая полуось;
cOFOF ==
21
– фокусное расстояние; прямые
1
D и
2
D – директрисы эллипса.
Канонические уравнение эллипса с центром в т.
)0;0(O
и полуосями
a
и
b
имеет
вид:
1
2
2
2
2
=+
b
y
a
x
. (2.1)
Фокусное расстояние можно определить из соотношения:
222
bac −=
;
эксцентриситет эллипса
)10(, <<=
εε
a
c
;
уравнения директрис
c
aa
x
2
=±=
ε
.
В случае, если
ab >
, то фокусное расстояние определяется
по формуле
222
abc −=
; эксцентриситет
b
c
=
ε
; уравнение директрис
ε
b
y
±=
.
Если центр эллипса находится в т.
),(
001
yxO
, то его уравнение
имеет вид:
1
)()(
2
2
0
2
2
0
=
−
+
−
b
yy
a
xx
(2.2)
В пространстве эллипсу соответствует эллипсоид. Его
каноническое уравнение (центр в т.
)0;0;0(
1
O и полуоси а, b,
с), имеет вид:
1
2
2
2
2
2
2
=++
c
z
b
y
a
x
(2.3)
Если же центр эллипсоида находится в т.
),,(
0001
zyxO
, то уравнение (2.3) преобразуется:
1
)()()(
2
2
0
2
2
0
2
2
0
=
−
+
−
+
−
c
zz
b
yy
a
xx
(2.4)
y
M
b
a
O
1
F
2
F
B
A
x
2
D
1
D
c
2
F
1
F
М
О
а
с
b
y
x
z
y
x
c
b
a

43
3. Гипербола и гиперболоиды
Определение. Гиперболой называется совокупность точек М плоскости,
абсолютная величина разности расстояний от которых до двух данных точек (фокусов
гиперболы) есть величина постоянная, т.е.
aconstMFMF 2
21
==−
.
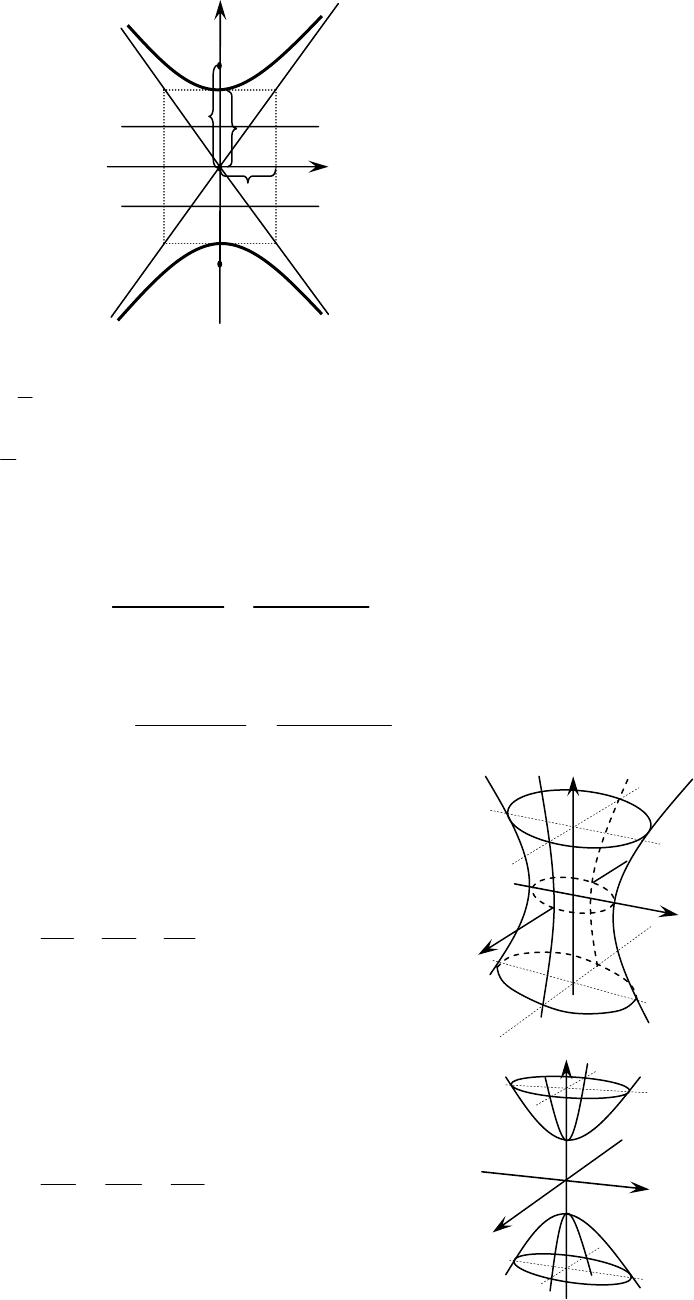
Здесь
21
FF - фокусы гиперболы,
a
– действительная полуось,
b
– мнимая полуось,
c
– фокусное расстояние,
1
D и
2
D – директрисы гиперболы,
1
C и
2
C – асимптоты
гиперболы. Каноническое уравнение гиперболы с центром в т.
)0;0(O
и полуосями:
действительной
a
и мнимой
b
имеет вид:
1
2
2
2
2
=−
b
y
a
x
(3.1)
Для гиперболы
222
bac +=
;
эксцентриситет эллипса
)1(, >=
εε
a
c
;
уравнения директрис
ε
a
x
±=
;
уравнение асимптот
x
a
b
y ±=
.
Гипербола, уравнение которой имеет вид
1
2
2
2
2
=+−
b
y
a
x
(3.2)
называется сопряженной с гиперболой (3.1) и имеет вид:
М
y
x
b
a
c
2
F
1
F
2
D
1
D
2
C
1
C
44
Здесь
a
– мнимая полуось,
b
– действительная полуось;
эксцентриситет эллипса
b
c
=
ε
;
уравнения директрис
ε
b
x
±=
.
Если центр гиперболы смещен в т.
),(
001
yxO
, то уравнение (3.1) и (3.2) принимают
вид:
1
)()(
2
2
0
2
2
0
=
−
−
−
b
yy
a
xx
(3.3)
1
)()(
2
2
0
2
2
0
=
−
+
−
−
b
yy
a
xx
(3.4)
В пространстве гиперболе соответствуют гиперболоиды:
однополостный и двухполостный.
Однополостный гиперболоид описывается уравнением
1
2
2
2
2
2
2
=−+
c
z
b
y
a
x
(3.5)
и имеет вид
двухполостный гиперболоид описывается уравнением
1
2
2
2
2
2
2
−=−+
c
z
b
y
a
x
(3.6)
4. Парабола и параболоиды
Определение. Параболой называется совокупность точек М плоскости, каждая из
которых равноудалена от данной точки (фокуса параболы) и данной прямой (директрисы
параболы) т.е.
M
D
F
M = .
2
F
1
F
2
D
1
D
a
b c
yx
z
y
x
z
45
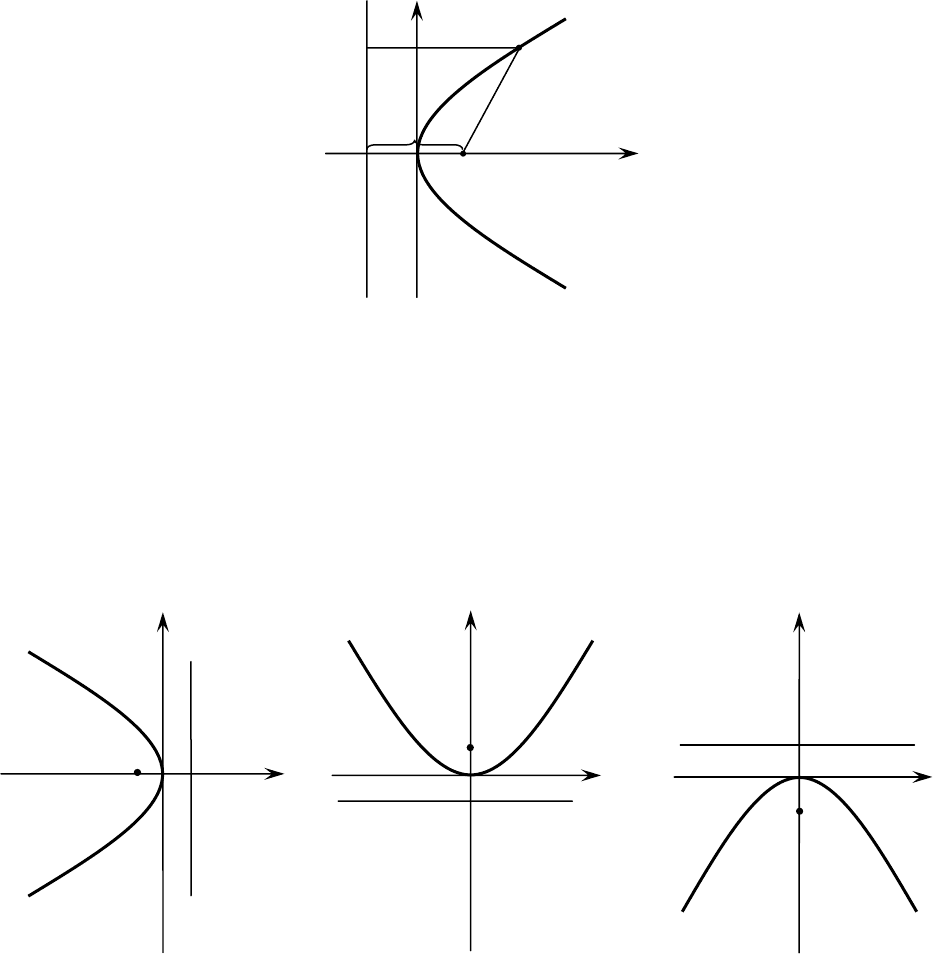
Здесь
F – фокус параболы, расстояние от директрисы до фокуса
pDF =
– параметр
параболы. Каноническое уравнение параболы с вершиной в т.
)0;0(O
, параметром р и
ветвями, направленными вправо имеет вид
pxy 2
2
=
(4.1)
Уравнения
pxy 2
2
−=
,
pyx 2
2
=
,
pyx 2
2
−=
определяют параболы, иначе
ориентированные относительно осей координат.
Если вершина параболы находится в т.
),(
001
yxO
, то ее уравнение выглядит одним
из следующих образов
)(2)(
0
2
0
xxpyy −=−
,
)(2)(
0
2
0
xxpyy −−=−
)(2)(
0
2
0
yypxx −=−
(4.2)
)(2)(
0
2
0
yypxx −−=−
В пространстве параболе соответствуют параболоиды: эллиптический и
гиперболический.
Эллиптический параболоид описывается уравнением
y
x
D
O F
F
y
D
x
O
y
x
D
O
F
х
y
M
F
D
p
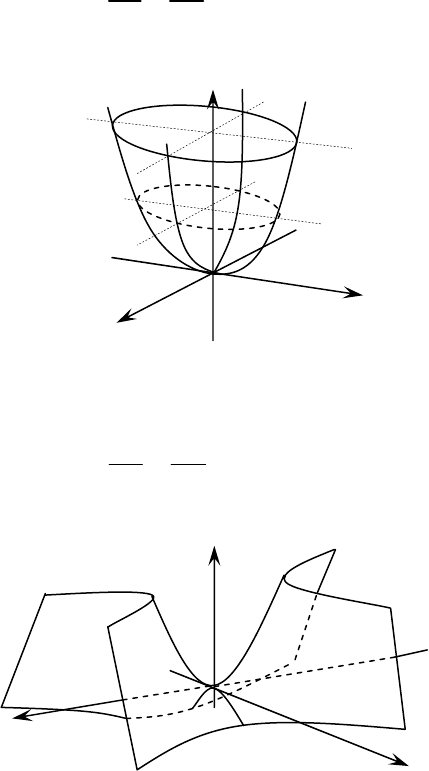
46
z
b
y
a
x
2
2
2
2
2
=+
(4.3)
и имеет вид
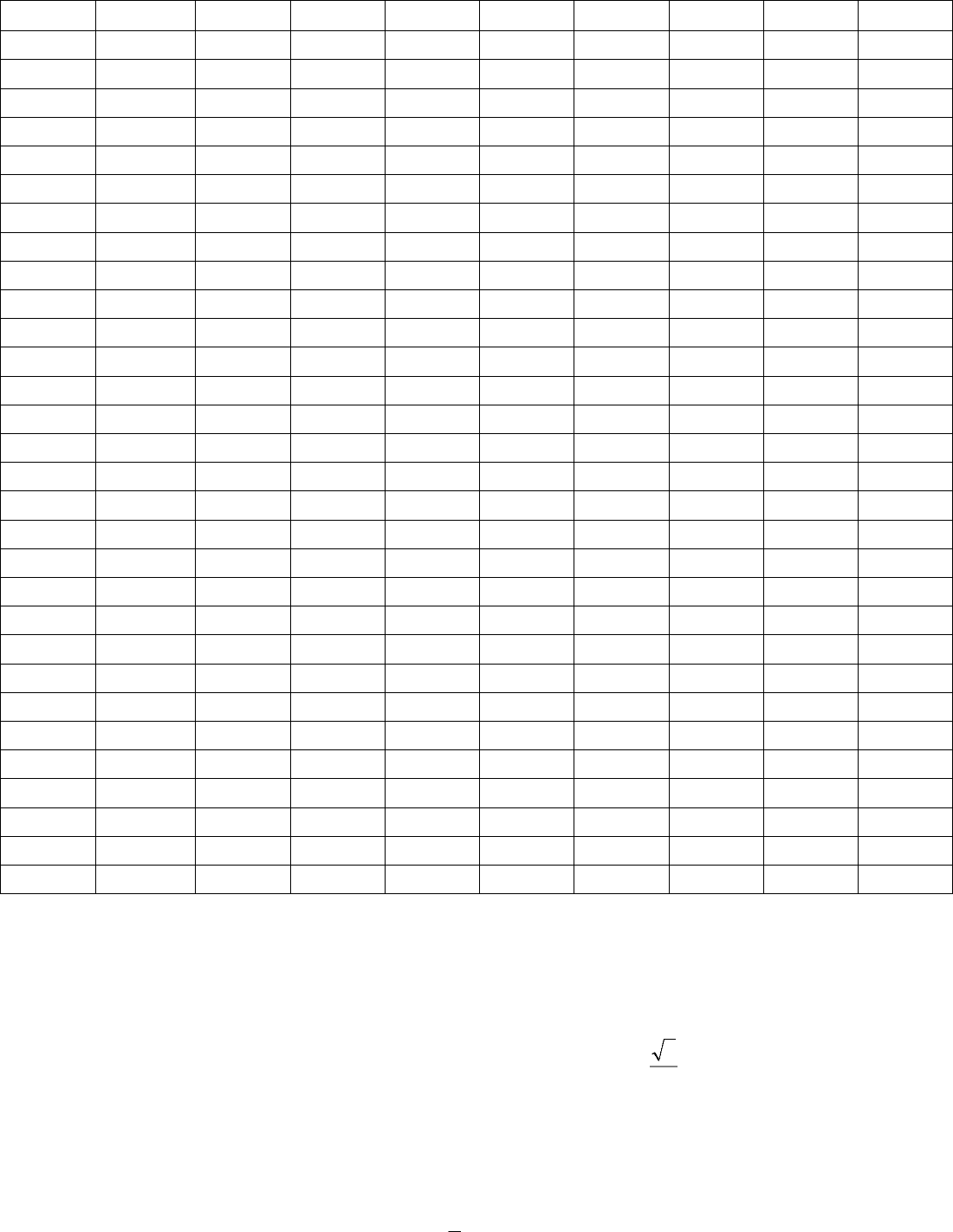
Гиперболический параболоид описывается уравнением
z
b
y
a
x
2
2
2
2
2
−=−
(4.4)
и имеет вид.
Задание 11
Построить кривые и записать их уравнения.
1. Окружность а) с центром в т.
)0;0(O
и радиусом
1
R ;
б) с центром в т. ),(
111
yxO и радиусом
2
R .
2. Эллипс а) с центром в т.
)0;0(O
и полуосями
1
a и
1
b ;
б) с центром в т.
),(
111
yxO и полуосями
2
a и
2
b .
3. Гипербола а) с центром в т.
)0;0(O
и полуосями
1
a – действительной,
1
b – мнимой и
сопряженную с ней гиперболу;
б) с центром в т.
),(
111
yxO и полуосями
2
a – действительной,
2
b – мнимой.
4. Парабола а) с вершиной в т.
)0;0(O
, параметром
1
p , ветви которой направлены
- вправо,
- влево,
- вверх,
- вниз;
б) с вершиной в т.
),(
111
yxO и параметром
2
p , ветви направлены вниз.
z
y
x
y
x
z
47
№ вар.
),(
111
yxO
1
R
2
R
1
a
1
b
2
a
2
b
1
p
2
p
1
(1;–2) 2 3 1 2 5 4 1 2
2
(3;0) 3 1 2 1 4 3 2 1
3
(–2;3) 4 2 2 3 3 2 1 3
4
(–1; 2) 1 3 2 4 3 1 2 3
5
(4, 5)
3 3 3 4 5 2 2 1
6
(5, 3)
1 2 4 5 4 3 2 1
7
(5, 3)
2 4 3 4 5 4 3 1
8
(3, 5)
1 3 2 4 2 1 2 3
9
(3, 2)
2 1 1 3 2 1 1 2
10
(–2, 1)
1 2 2 4 3 2 1 2
11
(4, 0)
3 4 2 5 4 1 2 3
12
(4, 5)
2 1 1 3 5 4 2 1
13
(6, 1)
4 3 2 3 5 3 3 1
14
(1, 2)
3 5 2 4 3 2 2 4
15
(1, –1)
1 2 2 5 5 4 3 1
16
(4, 5)
4 3 2 3 2 1 1 4
17
(3, 4)
1 2 2 4 4 2 2 5
18
(4, –2)
2 1 3 5 4 3 1 2
19
(0, –3)
3 4 2 3 4 2 3 4
20
(–2, 5)
1 1 4 5 3 1 2 3
21
(–3, 1)
1 5 3 4 2 1 4 1
22
(4, –1)
5 1 4 5 4 3 2 3
23
(3, 2)
1 5 2 5 5 4 3 3
24
(0, 4)
3 5 1 3 3 2 5 3
25
(–2, –3)
1 2 4 5 4 3 1 3
26
(–1, 2)
2 3 2 4 2 1 2 5
27
(1, –2,)
3 3 2 5 3 2 3 1
28
(–2, –4)
4 2 2 3 5 3 2 4
29
(4, 6)
1 4 1 2 3 2 3 1
30
(3, 5)
3 5 1 4 4 3 2 3
Задание 12
Решить задачи и построить фигуры.
1 вариант. Составить канонические уравнения: а) параболы, если ее фокус имеет
координаты (0; –3);
б) эллипса, если его эксцентриситет
3
3
=
ε
, большая полуось а = 3;
в) гиперболы, если расстояние между фокусами равно 10, а расстояние между
вершинами равно 8.
2 вариант. Составить канонические уравнения: а) эллипса, зная, что расстояние между
фокусами равно 24 и большая полуось равна 26;
б) гиперболы, если действительная
полуось равна 5 и эксцентриситет
3
5
=
ε
3; в) параболы, директриса которой имеет
уравнение
x + 2 = 0.

48
3 вариант. Составить канонические уравнения: а) эллипса, если большая полуось равна
5, а расстояние между фокусами – 8;
б) гиперболы, если она равносторонняя и проходит
через точку
M(2, 1); в) параболы, фокус которой имеет координаты (–5, 0).
4 вариант. Составить канонические уравнения: а) эллипса, если большая полуось равна
10 и эксцентриситет равен 0,8;
б) гиперболы, асимптоты которой заданы уравнениями
y = ±2x и фокусы находятся на расстоянии равном 5 от центра; в) параболы,
симметричной относительно оси ординат и проходящей через точку
М(5, 1).
5 вариант. Составить канонические уравнения: а) эллипса, если эксцентриситет
6,0=
ε
, а
расстояние между фокусами равно 6;
б) гиперболы, если расстояние между фокусами
равно 10, а расстояние между вершинами – 8;
в) параболы, директриса которой имеет
уравнение
у + 6 = 0.
6 вариант. Составить канонические уравнения: а) эллипса, расстояние, между
директрисами которого равно
154
, а
2
2
=
ε
; б) гиперболы, если расстояние между
директрисами равно 8 / 5 и эксцентриситет
2
3
=
ε
; в) параболы, если она проходит через
точку (–4, 4) и симметрична относительно оси
Ох.
7 вариант. Составить канонические уравнения: а) эллипса, расстояние, между
директрисами которого равно 12, а большая ось равна
32
; б) параболы, симметричной
относительно оси абсцисс и проходящей через точку
М(–1, 2); в) Найти длины осей,
координаты фокусов и эксцентриситет гиперболы, заданной каноническим уравнением
360025144
22
=− yx
.
8 вариант. а) Составить канонические уравнения: а) эллипса, если его эксцентриситет
5
3
=
ε
, а малая полуось b = 2; б) параболы, симметричной относительно оси ординат и
проходящей через точку
)2;32(−M
; в) Найти длины осей, координаты фокусов и
эксцентриситет гиперболы, заданной каноническим уравнением
144169
22
=− yx
.
9 вариант. Составить канонические уравнения: а) эллипса, расстояние, между фокусами
которого равно 8, а эксцентриситет
2
1
=
ε
; б) гиперболы, действительная полуось которого
равна 20 , и гипербола проходит через точку
N(–10, 4); в) параболы, фокус которой имеет
координаты (0, –3).
10 вариант. Составить канонические уравнения: а) эллипса, сумма полуосей которого
равна 18 и расстояние между фокусами – 12;
б) гиперболы, если даны равнения ее
асимптот
y = ±5x /12 и координаты точки М(24, 5), лежащей на гиперболе; в) параболы,
директриса которой имеет уравнение
х – 15 = 0.
11 вариант. Составить канонические уравнения: а) параболы, симметричной
относительно оси
Оx, с вершиной в начале координат и проходящей через точку
А(–2, –3); б) эллипса, если его большая полуось равна 12, а эксцентриситет равен 0,8;
в) гиперболы проходящей через точку (
22;6 −
) и имеющей мнимую полуось равную 2.
12 вариант. Составить канонические уравнения: а) эллипса, если малая полуось равна
24, а расстояние между фокусами 2
с = 10; б) гиперболы, если расстояние между
фокусами равно 6 и эксцентриситет
2
3
=
ε
; в) параболы, расположенной в правой
полуплоскости симметрично относительно оси
Оx, если ее параметр р = 3.
49
13 вариант. Составить канонические уравнения: а) гиперболы, если уравнения асимптот
y = ±4x / 3 и расстояние между фокусами 2с = 20; б) эллипса, если расстояние между
фокусами 2
с = 6 и эксцентриситет
5
3
=
ε
; в) параболы, симметричной относительно оси
Оx и проходящей через точку А(9; 6).
14 вариант. Составить канонические уравнения: а) гиперболы, если ее расстояние
между фокусами 2
с = 10 и мнимая ось равна 8; б) параболы, которая имеет фокус
F(0; –3), проходит через начало координат и симметрична относительно оси ординат;
в) эллипса, если большая ось равна 10, а расстояние между фокусами – 8.
15 вариант. Составить канонические уравнения: а) эллипса, если его полуоси равны
соответственно 7 и 2;
б) гиперболы, фокусы которой лежат на оси абсцисс, симметрично
относительно начала координат и даны точки
)1;6(
1
−M и
)22;8(
2
−M
, принадлежащие
гиперболе;
в) параболы, расположенной в нижней плоскости симметрично относительно
оси
Оу и ее параметр равен 3.
16 вариант. Составить канонические уравнения: а) гиперболы, имеющей вершины в
фокусах, а фокусы в вершинах эллипса
1
925
22
=+
yx
; б) эллипса, если расстояние между
фокусами равно 24, и эксцентриситет равен
13
12
; в) параболы, симметричной
относительно оси абсцисс и проходящей через точки (0, 0) и (1, –3).
17 вариант. Составить канонические уравнения: а) параболы, расположенной
симметрично относительно оси абсцисс и проходящей через точку
В(–1; 3);
б) гиперболы, фокусы которой лежат на оси абсцисс, симметрично относительно начала
координат и даны координаты точки
⎟
⎠
⎞
⎜
⎝
⎛
−1;
2
9
1
M , принадлежащей гиперболе, и уравнения
асимптот
3
2x
y
±=
; в) эллипса, фокусы которого расположены на оси абсцисс,
симметрично относительно начала координат, если даны точка
)2;52(−M
,
принадлежащая эллипсу, и его малая ось равная 3.
18 вариант. Составить канонические уравнения: а) эллипса, фокусы которого
расположены на оси абсцисс, симметрично относительно начала координат, если даны
точки
)3;4( −M
и
)3;22(N
принадлежащие эллипсу; б) гиперболы, фокусы которой
расположены на оси ординат симметрично относительно начала координат, кроме того,
расстояние между ними 20, а эксцентриситет
3
5
=
ε
; в) параболы, если дано уравнение
директрисы
х – 5 = 0.
19 вариант. Составить канонические уравнения: а) эллипса, фокусы которого
расположены на оси абсцисс, симметрично относительно начала координат, если даны
точка
⎟
⎠
⎞
⎜
⎝
⎛
−
3
5
;2M и эксцентриситет
3
2
=
ε
; б) гиперболы, фокусы которой расположены на
оси ординат симметрично относительно начала координат, кроме того, уравнения
асимптот
5
12x
y
±=
и расстояние между вершинами равно 48; в) параболы, если уравнение
ее директрисы
y + 1 = 0.
20 вариант. Составить канонические уравнения: а) параболы, проходящей через начало
координат и точку
D(4, –8), расположенной симметрично относительно оси ординат;
50
б) эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно
начала координат, если даны точка
)1;15(M
принадлежащая эллипсу и расстояние между
фокусами 2
с = 8; в) гиперболы, проходящей через точки А(2, 1) и В(
7;4−
).
21 вариант. Составить канонические уравнения: а) эллипса, проходящего через точки
М
1
(2; 3), М
2
(0; 2); б) параболы, если ее фокус F(4; 0) и вершина совпадает с началом
координат.
в) Для гиперболы, заданной уравнением
144916
22
=− yx
найти длины
полуосей, фокусы, уравнения асимптот.
22 вариант. а) Составить каноническое уравнение гиперболы, если она проходит через
точку
М(
2;3
) и ее эксцентриситет 2=
ε
. б) Найти полуоси, фокусы и эксцентриситет
эллипса
1694
22
=+ yx
. в) Найти координаты фокуса и уравнение директрисы параболы
y
2
= 12x .
23 вариант. а) Найти координаты фокуса и уравнение директрисы параболы x
2
= 8y .
б) Вычислить координаты фокусов и уравнения директрис гиперболы 1
169
22
=−
yx
;
в) Составить каноническое уравнение эллипса, проходящего через точки
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
4
6
;
2
5
M
,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
5
15
;2N
.
24 вариант. а) Определить длины полуосей и координаты фокусов эллипса x
2
+ 3y
2
= 6 .
б) Составить каноническое уравнение гиперболы, пересекающей ось Оу и проходящей
через точки
М(
55;24
), N(0, 5). в) Найти координаты фокуса и уравнения директрисы
параболы
yx 16
2
−=
.
25 вариант. а) Составить каноническое уравнение эллипса, полуоси которого равны,
соответственно 3 и 6.
б) Найти уравнение гиперболы, вершины и фокусы которой
находятся в соответствующих вершинах и фокусах эллипса
1
58
22
=+
yx
. в) Найти
координаты фокусов и уравнение директрисы параболы
y
2
= 6x .
26 вариант. а) Составить каноническое уравнение эллипса, если две его вершины
находятся в точках
А
1
(8, 0) и А
2
(–8, 0), а фокусы – в вершинах F
1
(5, 0) и F
2
(–5, 0).
б) Написать каноническое уравнение гиперболы, проходящей через точку (2, 1) и
асимптоты которой
4
3x
y
±=
. в) Написать уравнение параболы с вершиной в начале
координат, для которой директрисой служит прямая
х = –2.
27 вариант.а) Дан эллипс 1
1236
22
=+
yx
и точка на нем с абсциссой, равной 3. Найти ее
ординату.
б) Найти координаты фокусов гиперболы 1
25144
22
=−
yx
. в) Написать
каноническое уравнение параболы с вершиной в начале координат и директрисой
x = 3.
28 вариант. а) Написать каноническое уравнение гиперболы, если ее фокусы находятся
в точках
F
1
(–4, 0) и F
2
(4, 0) и длина действительной оси равна 6. б) Составить
каноническое уравнение параболы с вершиной в начале координат и фокусом
F(0, –5).
в) Найти уравнение равносторонней гиперболы, проходящей через точку (3,–1).
