Григоров О.В., Петренко Н.О. Вантажопідйомні машини
Подождите немного. Документ загружается.

240 241Î. Â. Ãðèãîðîâ, Í. Î. Ïåòðåíêî Âàíòàæîï³äéîìí³ ìàøèíè
;
2 4
L a
x =−
2
max
2
.
2 4
P L a
M
L
⎛⎞
=⋅−
⎜⎟
⎝⎠
Ïðè ðîçðàõóíêàõ ñóö³ëüíîñò³ííèõ ìîñò³â âèêîðèñòîâóþòüñÿ ôîðìóëè,
ùî âðàõîâóþòü îñíîâí³ íàâàíòàæåííÿ ÷è îñíîâí³ ³ äîäàòêîâ³
íàâàíòàæåííÿ.
24.2. Ðîçðàõóíîê ìàêñèìàëüíèõ íîðìàëüíèõ íàïðóæåíü
1. Ðîçðàõóíêîâ³ ôîðìóëè, ùî âèêîðèñòîâóþòü îñíîâí³ íàâàíòà-
æåííÿ:
[]
max max
1
,
q p
xx
KM M
W
⋅+ψ⋅
σ= σ
J
äå
max
q
M
ìàêñèìàëüíèé çãèíàëüíèé ìîìåíò â³ä ïîñò³éíîãî íà-
âàíòàæåííÿ;
max
p
M
ìàêñèìàëüíèé çãèíàëüíèé ìîìåíò â³ä ðóõîìîãî íàâàí-
òàæåííÿ;
xx
W
ìîìåíò îïîðó ïåðåòèíó ùîäî îñ³ õ;
[]
1
σ
ïåðøà ìåæà íàïðóæåíü, ùî äîïóñêàþòüñÿ.
2. Ðîçðàõóíêîâ³ ôîðìóëè, ùî âðàõîâóþòü äîäàòêîâ³ íàâàíòà-
æåííÿ:
[]
max max max
ãîðèçîíò
2
,
q p
xx yy
KM M M
WW
⋅+ψ⋅
σ= + σ
∑
J
äå
max
ãîðèçîíò
M
∑
ñóìàðíèé ìîìåíò â³ä ³íåðö³éíèõ ñèë, â³ä âëàñíî¿
âàãè, êîðèñíîãî ³ â³òðîâîãî íàâàíòàæåííÿ. Äëÿ Ñò 3
[]
1
σ
=140
ÌÏà,
[]
2
σ
=170 ÌÏà äðóãà ìåæà íàïðóæåíü, ùî äîïóñêàþòüñÿ.
Äëÿ íèçüêîëåãîâàíèõ ñòàëåé
[]
1
σ
=210 ÌÏà,
[]
2
σ
=250ÌÏà; äðó-
ãà ìåæà íàïðóæåíü, ùî äîïóñêàþòüñÿ, ìຠá³ëüøå çíà÷åííÿ, í³æ
ó ïåðøî¿ ìåæ³ íàïðóæåíü òîìó, ùî ö³ äîäàòêîâ³ ìîìåíòè òèì÷à-
ñîâî ä³þ÷³.
24.3. ϳäðàõóíîê ìàêñèìàëüíèõ ïåðåð³çíèõ íàïðóæåíü
1. Ïðè óðàõóâàíí³ îñíîâíèõ íàâàíòàæåíü:
()( )
[]
max maxmax max
ñêð, ñêð,
1
min 0
,
22
q p
q p
x
xx ïñ
KM MKT T
S
J hb
⋅+ψ⋅
⋅+ψ⋅
′
τ= ⋅ + τ
δ⋅ δ ⋅ +δ ⋅ +δ
J
äå
max
,
2
q
q L
T
⋅
=
Í ìàêñèìàëüíà ïîïåðå÷íà ñèëà â³ä ïîñò³éíîãî
êîëè â³í ðóõàºòüñÿ âë³âî. Åïþðà çãèíàëüíèõ ìîìåíò³â â³ä ïîñò³éíîãî
íàâàíòàæåííÿ âëàñíî¿ âàãè q áóäå ìàòè âèä ïàðàáîëè. Åïþðà ïîïåðå÷íèõ
ñèë, ùî ï
åðåð³çóþòü, â³ä ïîñò³éíîãî íàâàíòàæåííÿ âëàñíî¿ âàãè q ìàº
âèä ïðÿìî¿ ë³í³¿.
Ïîáóäóºìî åïþðó ïîïåðå÷íèõ ñèë ³ çãèíàëüíèõ ìîìåíò³â äëÿ
ðóõîìîãî íàâàíòàæåííÿ.
1. Âèçíà÷èìî R
A
. Ñêëàäåìî ð³âíÿííÿ ð³âíîâàãè íàâêîëî òî÷êè Â,
òîä³
()( )
0;
A
R L P Lx P Lxa
⋅−⋅ − −⋅ −− =
()
()
2 ;
A
R L P Lx a
⋅=⋅ ⋅ − −
()
2 .
A
P
R Lx a
L
=⋅⎡⋅−−⎤
⎣⎦
Ç öüîãî âèðàçó âèïëèâàº, ùî R
A
çì³íþºòüñÿ çà çàêîíîì ïðÿìî¿
ë³í³¿. Ðîçãëÿíåìî ² ïîëîæåííÿ â³çêà, òîä³ õ = La:
.
A
P a
R
L
⋅
=
Ðîç-
ãëÿíåìî ²I ïîëîæåííÿ â³çêà, òîä³ õ=0:
2 .
A
P a
RP
L
⋅
=−
ßêùî öþ ë³í³þ ïðîäîâæèòè, òî âîíà ïîòðàïèòü ó ò. Ð. Äîêàç
öüîãî: âíàñë³äîê òîãî, ùî òðèêóòíèêè ïîä³áí³, òî
,
P L
y a
=
çâ³äñè
,
P a
y
L
⋅
=
òîáòî
()
.xLa
=−
Öÿ ë³í³ÿ íàçèâàºòüñÿ ë³í³ºþ âïëèâó
(Ë.Â.) îïîðíî¿ ðåàêö³¿ R
A
. Öÿ ë³í³ÿ â òîé æå ÷àñ çîáðàæóº çíà÷åí-
íÿ ñèëè, ùî ïåðåð³çóº, ó ïåðåòèí³.
2. Âèçíà÷èìî åïþðó Ì
çãèí
â³ä ðóõîìîãî íàâàíòàæåííÿ:
() ()
()
2
22,
A
PP
M x R xLxa xLxxax
LL
⎡⎤
=⋅=⋅⎡⋅−−⎤⋅=⋅⋅ − −
⎣⎦
⎣⎦
òîáòî çãèíàëüíèé ìîìåíò çì³íþºòüñÿ çà çàêîíîì êâàäðàòè÷íî¿
ïàðàáîëè. Âèçíà÷èìî òî÷êó, äå Ì(õ) ìຠìàêñèìàëüíå çíà÷åííÿ.
³çüìåìî ïîõ³äíó:
() ()
/
22 0,
P
M xLxa
L
=⋅⎡⋅ − −⎤=
⎣⎦
òîáòî
.
2 4
L a
x =−
Àíàë³çóþ÷è âèðàç Ì(õ), ìîæíà ïðèéòè äî âèñíîâêó, ùî Ì(õ) = 0
ïðè: 1) õ = 0; 2)
()
2 0,Lx a
−−=
òîáòî õ = 0 òà
2
a
xL=−
ìàêñè-
ìàëüíå çíà÷åííÿ Ì
çãèí
â³ä ðóõîìîãî íàâàíòàæåííÿ ïðè
242 243Î. Â. Ãðèãîðîâ, Í. Î. Ïåòðåíêî Âàíòàæîï³äéîìí³ ìàøèíè
Ó ãîðèçîíòàëüíîìó íàïðÿìêó ä³þòü ñèëè ³íåðö³¿ ³ â³òðîâèõ íàâàíòà-
æåíü.
24.4. Ðîçðàõóíîê ñóö³ëüíîñò³ííèõ ìîñò³â íà æîðñòê³ñòü
³í çâîäèòüñÿ äî âèçíà÷åííÿ ìàêñèìàëüíîãî ïðîãèíó â³ä ðóõî-
ìîãî íàâàíòàæåííÿ. Ïðîãèí
() ()
[]
2
2
max
[3 ]
,
48700
xx
P L a LLa
L
ff
EJ
⋅−⋅ −−
==
J
äå à áàçà â³çêà;
L ïðîã³í, àëå êðàùå
[]
1000
L
f
=
äëÿ êðàí³â, ïðàöþþ÷èõ
ó âàæêîìó ðåæèì³ ðîáîòè.
íàâàíòàæåííÿ (ìàêñèìàëüíà îïîðíà ðåàêö³ÿ â³ä ïîñò³éíîãî íàâàíòàæåí-
íÿ);
max
p
T
ìàêñèìàëüíà ïîïåðå÷íà ñèëà â³ä ðóõîìîãî íàâàíòà-
æåííÿ;
2
/
2 4
ï c
x ïï
hh
S b
+δ δ ⋅
⎛⎞
=⋅δ⋅ +
⎜⎟
⎝⎠
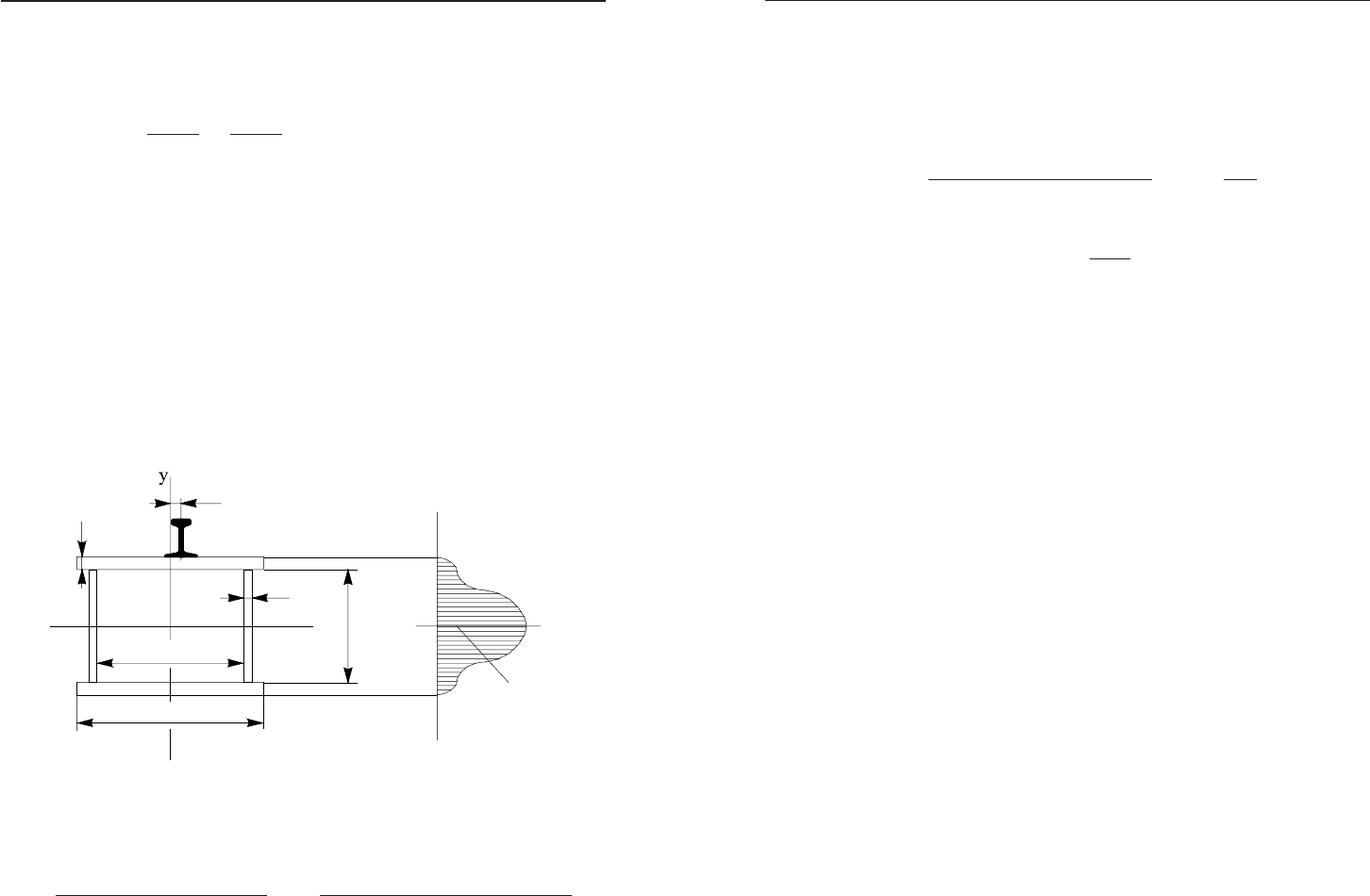
ñòàòè÷íèé ìîìåíò íàï³âïåðåòè-
íó ãîëîâíî¿ áàëêè â³äíîñíî îñ³ õõ (ðèñ. 24.2);
J
xõ
çãèíàëüíèé ìîìåíò ³íåðö³¿ ïîïåðå÷íîãî ïåðåð³çó â³äíîñ-
íî îñ³ õõ;
max
ñêð,
q
M
ìàêñèìàëüíèé ìîìåíò, ùî ñêðó÷óº, â³ä ïîñò³éíîãî
íàâàíòàæåííÿ;
max
ñêð,
p
M
ìàêñèìàëüíèé ìîìåíò, ùî ñêðó÷óº, â³ä ðóõîìîãî
íàâàíòàæåííÿ, çÿâëÿºòüñÿ ÷åðåç åêñöåíòðèñèòåò
∆
ðåéêè ùîäî îñ³
ñèìåò𳿠áàëêè (ðèñ. 24.2). Åêñöåíòðèñèòåò íå ïîâèííèé áóòè á³ëü-
øèì, í³æ 0,1 â³ä øèðèíè b
ï
ãîëîâíî¿ áàëêè:
0,1 ;
n
b
∆ J
min
δ
ì³í³ìàëüíà òîâùèíà ñò³íêè àáî ïîÿñó.
Íà ðèñ. 24.2 çîáðàæåíî ðîçïîä³ë ïåðåð³çíèõ íàïðóæåíü âíàñë³-
äîê çãèíó âçäîâæ îñ³ óó áàëêè (áåç óðàõóâàííÿ íåñó÷î¿ çäàòíîñ-
ò³ ðåéêè).
y
b
ï
õ
d
ï
b
0
d
ñ
D
t
max
y
õ
h
y
Ðèñ. 24.2. Ïåðåð³ç ãîëîâíî¿ áàëêè ³ ðîçïîä³ë ïåðåð³çíèõ íàïðóæåíü
âíàñë³äîê çãèíó
2. Ïðè óðàõóâàíí³ îñíîâíèõ ³ äîäàòêîâèõ íàâàíòàæåíü
()( )
max max maxmax max max
ñêð, ñêð, ãîðãîð
0
.
22
q p
q p
x
xx ïñ
KM M MKT T T
S
J hb
⋅+ψ⋅+
⋅+ψ⋅+
′
τ= ⋅ +
δδ⋅+δ⋅+δ
244 Î. Â. Ãðèãîðîâ, Í. Î. Ïåòðåíêî
v
1
u
2
b
D
2
D
1
u
1
o
1
o
2
v
2
a
D
3
o
3
a
P
R
A
P
S
D
3
H
S
D
4
Ö
2
D
4
Ö
1
H
o
4
v
3
o
5
So
4
-
o
5
Su
2
P
P
Ë.Â.
R
A
P a
l
×
y
y
Ðîçä³ë 25
ÐÎÇÐÀÕÓÍÎÊ ÐÅزÒ×ÀÑÒÈÕ ÌÎÑÒ²Â
25.1. Ðîçðàõóíîê çóñèëü â³ä ïîñò³éíîãî íàâàíòàæåííÿ
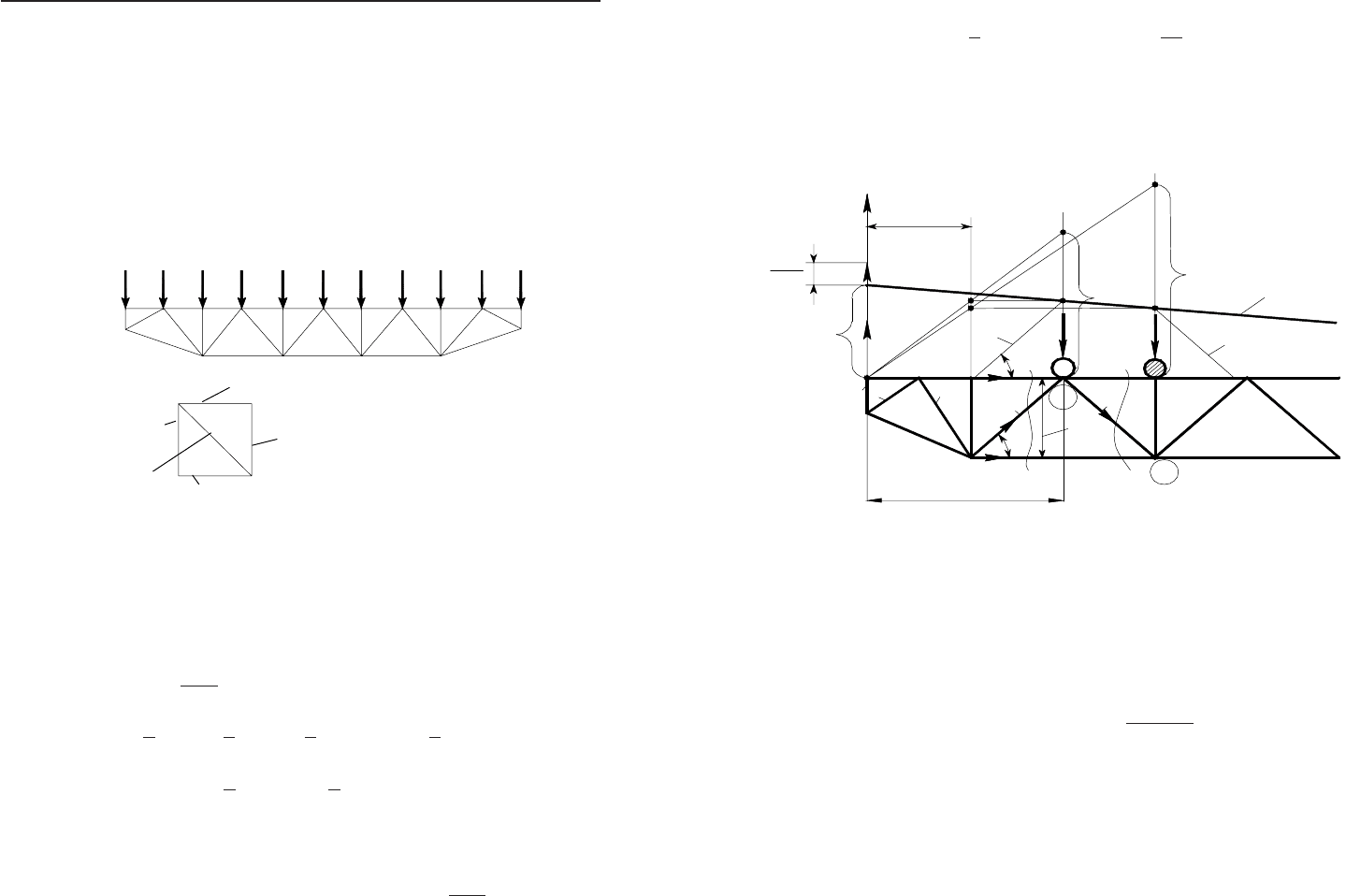
Ðîçðàõóíîê ðåø³ò÷àñòèõ ìîñò³â çâîäèòüñÿ äî âèçíà÷åííÿ ìàê-
ñèìàëüíèõ çóñèëü â åëåìåíòàõ ôåðì ³ ïðè ï³äáîð³ ïåðåòèí³â.
Çóñèëëÿ ñêëàäàþòüñÿ ç çóñèëü â³ä ïîñò³éíîãî íàâàíòàæåííÿ
(ðèñ. 25.1) ³ â³ä
ðóõîìîãî íàâàíòàæåííÿ.
Ðèñ. 25.2. Âèçíà÷åííÿ çóñèëü â³ä ðóõîìîãî íàâàíòàæåííÿ
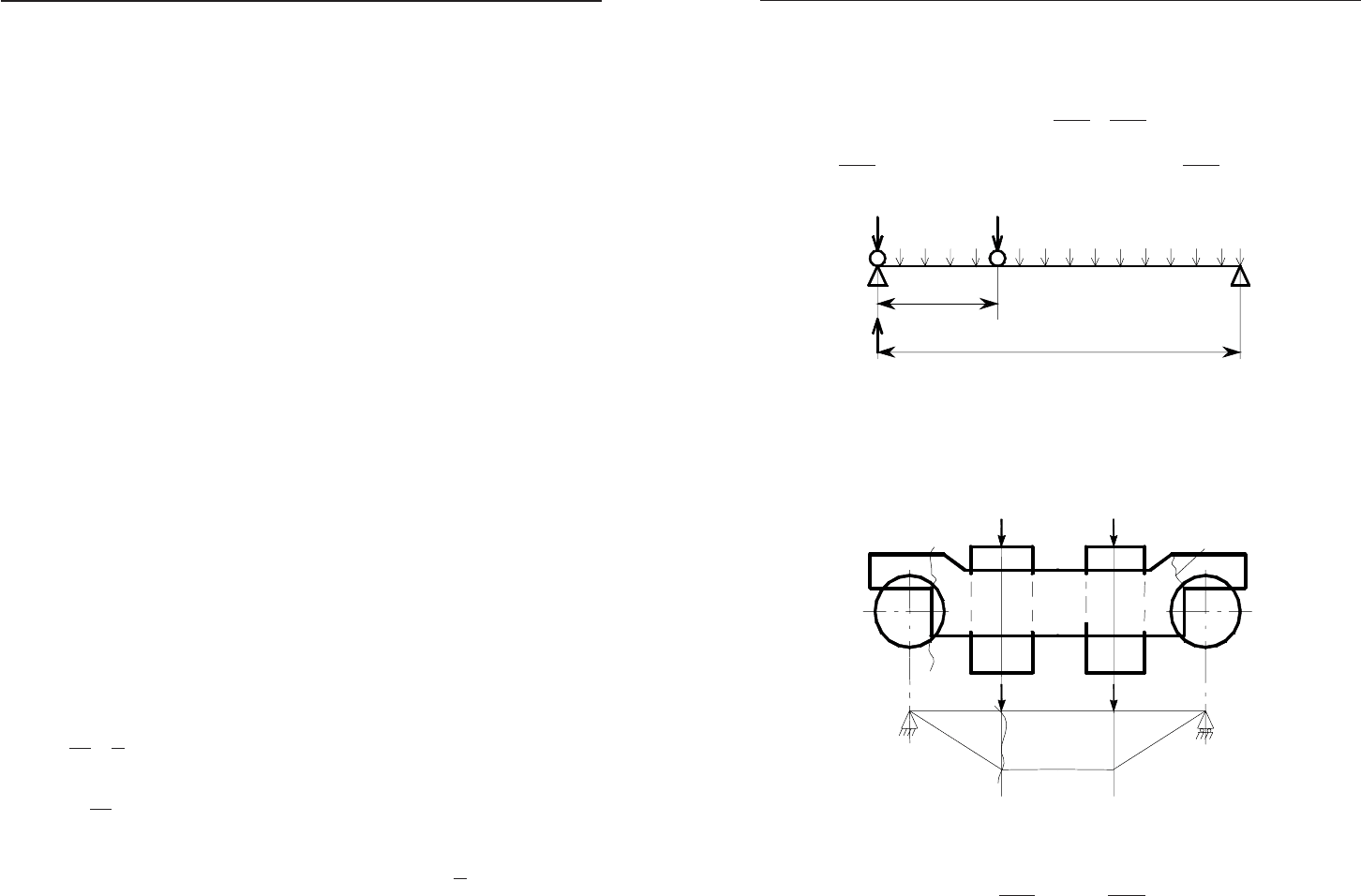
Âèçíà÷åííÿ çóñèëëÿ
2
u
S
.
Ïðèïóñòèìî, ùî ïåðåäíº êîëåñî â³çêà âñòàíîâëåíî â ïîçèö³¿
(Ö1). Äëÿ âèçíà÷åííÿ
2
u
S
ðîçð³æåìî óìîâíî ôåðìó ³ â³çüìåìî
Ö1
0;
M =
∑
ïðè öüîìó â³äêèíåìî ïðàâó ÷àñòèíó ôåðìè, ÿê ïîêàçà-
íî íà ðèñ. 25.1.
() 2
;
A D u
R b SH
⋅= ⋅
()
2
,
A D
u
R b
S
H
⋅
=
45
OO
S
−
âèçíà÷àºòüñÿ ÷åðåç
MΣ
â³äíîñíî öåíòðà Ö2.
4
D
S
âèçíà-
÷àºòüñÿ ïðè ïðîåêö³¿ óñ³õ ñèë
FΣ
íà â³ñü ó â òî÷ö³ Î5.
3
D
S
âèçíà-
÷àºòüñÿ ïðè ïðîåêö³¿ óñ³õ ñèë
FΣ
íà â³ñü ó â òî÷ö³ Ö1.
Âèñíîâîê: 1. Çóñèëëÿ çàëåæèòü â³ä çãèíàëüíîãî ìîìåíòó ³ ïîëî-
æåííÿ íà ïðîëüîò³.
2. Ðîçðàõóíêîâèìè º ò³ ñòðèæí³, ùî ðîçòàøîâàí³ â ñåðåäí³é
÷àñòèí³ ôåðìè.
qqqqqqq
q/2
q/2
qq
âåðõíÿ ãàëüì³âíà ôåðìà
íèæíÿ ãàëüì³âíà ôåðìà
áîêîâà ôåðìà
ãëàâíà
ôåðìà
ä³àãîíàëüí³
çâÿçêè
Ðèñ. 25.1. Ðîçïîä³ë íàâàíòàæåíü ïî âóçëàõ ðåø³ò÷àñòîãî ìîñòà â³ä
ïîñò³éíîãî íàâàíòàæåííÿ
Çóñèëëÿ âèçíà÷àþòüñÿ çà ä³àãðàìîþ ÌàêñâåëëàÊðåìîíè.
Ôåðìà ñèìåòðè÷íà, òîìó áóäóºìî çóñèëëÿ äëÿ ïîëîâèíè ôåðìè.
×åðåç
/
ã.ô
G
ïîçíà÷èìî çâåäåíó âàãó ãîëîâíî¿ ôåðìè ÷åðåç n ÷èñëî
âóçë³â ïî âåðõíüîìó ïîÿñó ôåðìè. Äâà êðàéí³õ âóçëè ïðèéìàºìî çà
îäèí âóçîë, òîä³
/
ã.ô
1
G
q
n
=
−
; q íàâàíòàæåííÿ ó âóçë³ (äèâ. ðèñ. 25.1);
/
ã.ôã.ô â.ã.ôí.ã.ô ì-ìóïåðåñóâ ä³àãîí.çâ'ÿçê³â
111 1
222 2
GG G G G G=+⋅ +⋅ +⋅ +⋅ +
íàñòèëó á.ì
11
.
22
GG+⋅ +⋅
Äëÿ êðàí³â
5 39Q
=÷
ò âàãè ãîëîâíî¿ ôåðìè ìîæíà ï³äðàõóâà-
òè îð³ºíòîâíî çà ôîðìóëîþ:
()
ã.ô
5 7000,
G Q L
=−+
Í, äå Q ó êÍ;
L ïðîã³í, ì;
áîê.ôåðìè
G
ïðèáëèçíî äîð³âíþº
ã.ô
2
G
;
ãàëüì.ôåðìè
G
ïðèáëèçíî äîð³âíþº
ã.ô
1
3
G
;
ä³àãîí.çâ'ÿçê³â ã.ô
1
30
GG≅
;
ì-ìóïåðåñóâ
G ≅
0,7 1,3
≅÷
ò;
áóäêè ìàøèí³ñòà
G ≅
äî 1,5 ò.
25.2. Âèçíà÷åííÿ çóñèëü â åëåìåíòàõ ãîëîâíî¿ ôåðìè â³ä
ðóõîìîãî íàâàíòàæåííÿ
246 247Î. Â. Ãðèãîðîâ, Í. Î. Ïåòðåíêî Âàíòàæîï³äéîìí³ ìàøèíè
Ðîçðàõóíêîâ³ ôîðìóëè äëÿ åëåìåíò³â ãîëîâíî¿ ôåðìè
ðåø³ò÷àñòîãî ìîñòà
Ñòðèæí³ âåðõíüîãî ïîÿñó
Íàéìåíó-
âàííÿ
Ç óðàõóâàííÿì îñíîâíèõ íàâàíòàæåíü
Ç óðàõóâàííÿì îñíîâíèõ ³
äîäàòêîâèõ íàâàíòàæåíü
Ïðè ïåðå-
â³ðö³ íà
ì³öí³ñòü
[]
max
çã
max
íåòòî íåòòî
max
1 çã
â
, äå
6
q p
K SS
Ì
FF
Ð
Ì
× +
y
×
y
×
s=--
×
s=
J
J
[]
1 2
max
íåòòî
max max
çã çã
2
íåòòî
íåòòî
q p
y
x
K SSSS
F
ÌÌ
W
W
× +y× ++
s=--
y ×
-- s
J
Ïðè ïåðå-
â³ðö³ íà
ñò³éê³ñòü
[]
max
á
ðó
òòî
max
çã
1
á
ðó
òòî
q p
x
K SS
F
Ì
W
× +y ×
s=--
j×
y ×
- sJ
[]
1 2
max
áðóòòî
max max
çã çã
2
íåòòî
íåòòî
q p
õ
y
x
K SSSS
F
ÌÌ
W
W
× +y × ++
s=--
j ×
y ×
-- sJ
Ñòðèæí³ íèæíüîãî ïîÿñó
Íàéìåíó-
âàííÿ
Ç óðàõóâàííÿì îñíîâíèõ íàâàíòàæåíü
Ç îáë³êîì îñíîâíèõ ³ äîäàòêîâèõ
íàâàíòàæåíü
Ïðè ïåðå-
â³ðö³ íà
ì³öí³ñòü
[]
max 1
íåòòî
q p
K SS
F
× +y ×
s= sJ
[]
1
max
íåòòî
2
,
q p
K SSS
F
× +
y
× +
s=
sJ
S
2
íåìàº, òîìó ùî íèæí³é ïîÿñ íå
ñïðèéìຠ³íåðö³éí³ ñèëè â³ä
ðóõîìîãî íàâàíòàæåííÿ
Ïðè ïåðå-
â³ðö³ íà
ñò³éê³ñòü
ijàãîíàë³ ³ ñò³éêè
Íàéìåíó-
âàííÿ
Ç óðàõóâàííÿì îñíîâíèõ
íàâàíòàæåíü
Ç îáë³êîì îñíîâíèõ ³ äîäàòêîâèõ
íàâàíòàæåíü
Ïðè ïåðå-
â³ðö³ íà
ì³öí³ñòü
max 1
íåòòî
q p
K SS
F
× +y ×
s=- sJ
ä.á 1 2
max 2
íåòòî
q p
K SSSSS
F
× +y × +++
s=- sJ
Ïðè ïåðå-
â³ðö³ íà
ñò³éê³ñòü
[]
max 1
áðóòòî
q p
õ
K SS
F
× +y ×
s=- s
j ×
J
[]
ä.á 1 2
max 2
á
ðó
òòî
q p
õ
K SSSSS
F
× +
y
× +++
s=- s
j
×
J
Sq çóñèëëÿ â ñòðèæí³ â³ä ïîñò³éíîãî íàâàíòàæåííÿ (ç ä³àãðà-
ìè ÌàêñâåëëàÊðåìîíè).
Sp çóñèëëÿ â ñòðèæí³ â³ä ðóõîìîãî íàâàíòàæåííÿ (âèçíà÷à-
ºòüñÿ íà ï³äñòàâ³ ë³í³é âïëèâó).
3. Óñ³ ñòðèæí³ íèæíüîãî ïîÿñó ðîçòÿã
íóò³.
Àíàëîã³÷íî äëÿ âåðõíüîãî ïîÿñó:
1. Óñ³ ñòðèæí³ ñòèñíóò³.
2. Ðîçðàõóíêîâ³ ñòðèæí³ çíàõîäÿòüñÿ ïîñåðåäèí³ êðàíà.
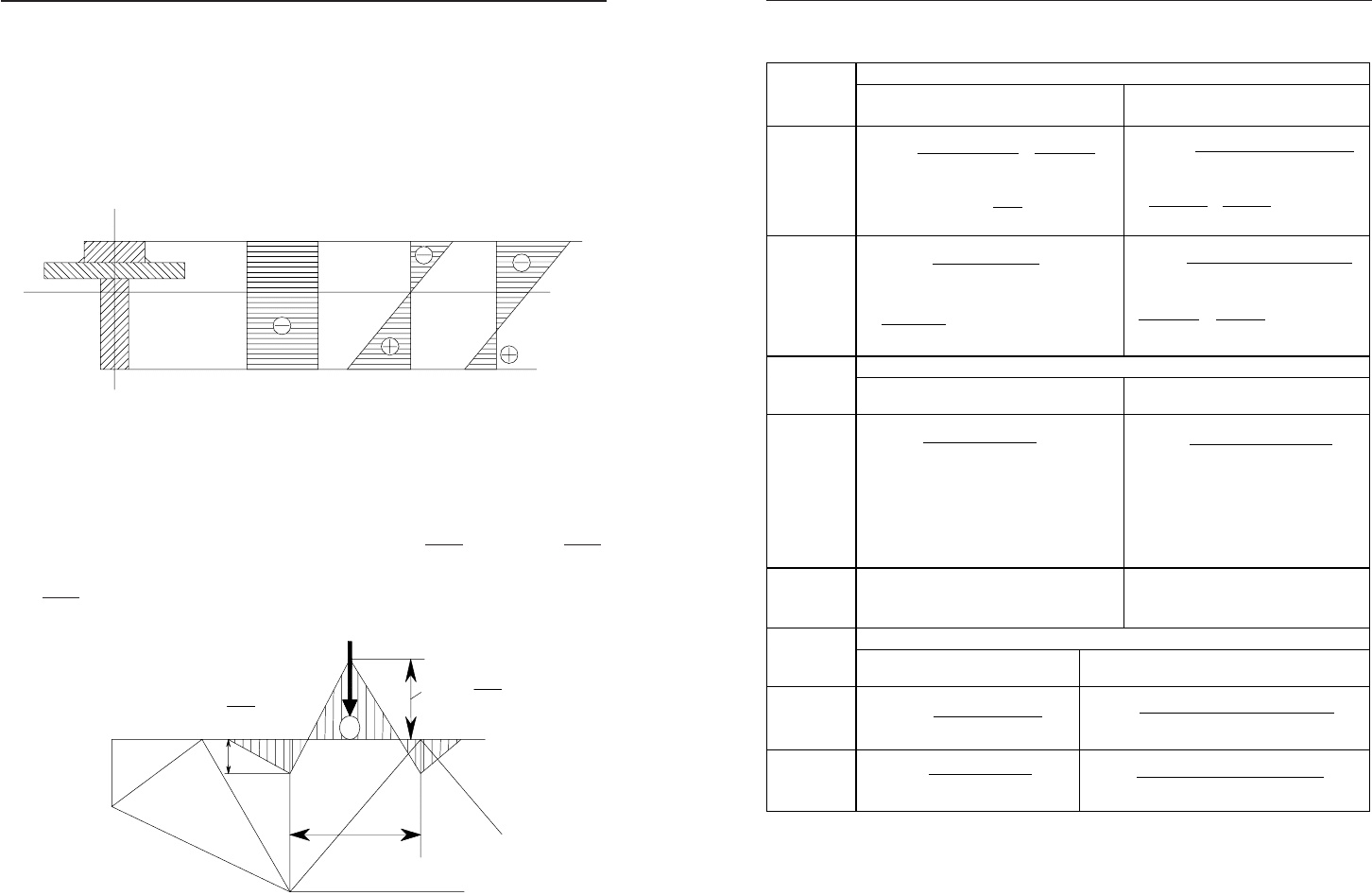
Åëåìåíòè âåðõíüîãî ïîÿñó ãîëîâíî¿ ôåðìè çàçíàþòü íå ò³ëüêè
ñòèñêàëüíèõ çóñèë
ü, àëå ³ ì³ñöåâîãî âèãèíó â³ä ðóõîìîãî íàâàíòà-
æåííÿ (ðèñ. 25.3).
Ðèñ. 25.3. Åïþðà íàïðóæåíü ó ñòðèæíÿõ âåðõíüîãî ïîÿñó
õ õ
ñòèñíåííÿ
ì³ñöåâèé
çãèí
ñóìàðí³
íàïðóæåííÿ
Ñòðèæí³ âåðõíüîãî ïîÿñó ìîæóòü çãèíàòèñÿ ó âåðòèêàëüí³é ³ â ãî-
ðèçîíòàëüí³é ïëîùèí³ (â³ä ïóñêó ³ ãàëüìóâàííÿ). Íàï³âïàíåëü âåðõ-
íüîãî ñòèñíóòîãî ïîÿñó íå ìîæå áóòè ðîçãëÿíóòà ÿê áàëêà
, ùî
îá³ïåðòà íà äâîõ îïîðàõ ³ íå ìîæå áóòè ðîçãëÿíóòà ÿê áàëêà ç
æîðñòêî çàòèñíóòèìè ê³íöÿìè. Òîìó
max
6
P b
M
⋅
=
, çàì³ñòü
4
P b⋅
àáî
8
P b⋅
, òîáòî áåðåìî ñåðåäíº çíà÷åííÿ.
Ðèñ. 25.4. Çãèíàëüíèé ìîìåíò â ñòðèæíÿõ âåðõíüîãî ïîÿñó
b
P
12
P b
M
×
»
max
çã
6
P b
M
×
»
248 249Î. Â. Ãðèãîðîâ, Í. Î. Ïåòðåíêî Âàíòàæîï³äéîìí³ ìàøèíè
À
q (Í/ì)
À
Ð
Ð
b
L
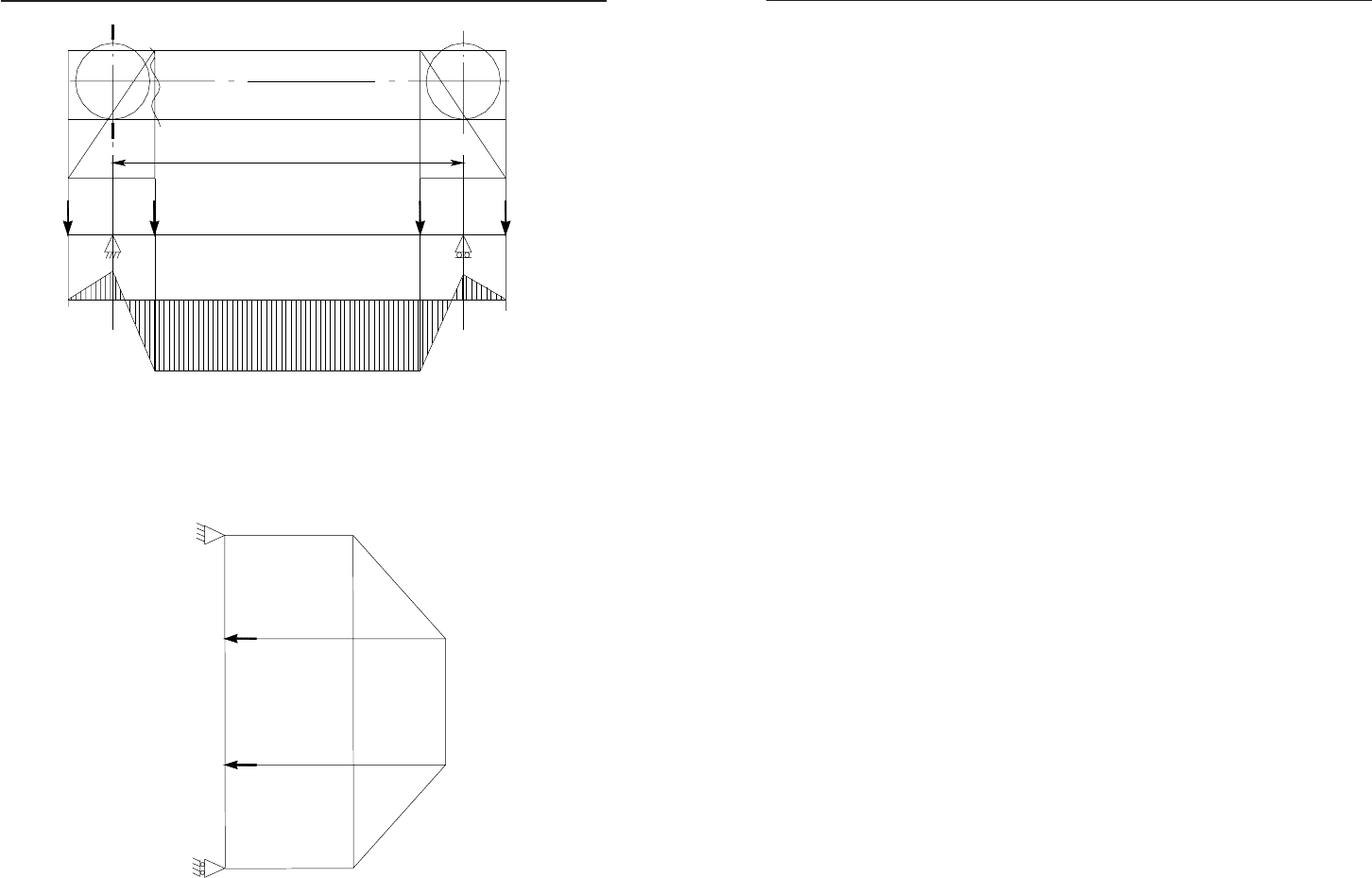
25.4. Ðîçðàõóíîê ê³íöåâèõ áàëîê
Íà ðèñ. 25.5 ñõåìàòè÷íî çîáðàæåí³ íàâàíòàæåííÿ óçäîâæ ïðî-
ëüîòó ìîñòà.
2 ,
2
A
P b q L
RP
L
⋅⋅
=− +
2
P b
P
L
⋅
−
â³ä ðóõîìîãî íàâàíòàæåííÿ;
2
q L⋅
â³ä âëàñíî¿
âàãè ìîñòà.
Ðèñ. 25.5. Ðîçïîä³ë íàâàíòàæåíü óçäîâæ ïðîëüîòó ìîñòà
Íà ðèñ. 25.6 çîáðàæåíà ñõåìà ê³íöåâî¿ áàëêè ìîñòà ñóö³ëüíî-
ñò³ííî¿ êîíñòðóêö³¿, à íà ðèñ. 25.7 ñõåìà ê³íöåâî¿ áàëêè ðåø³ò÷à-
ñòî¿ êîíñòðóêö³¿ òà åïþðè çãèíàëüíîãî ìîìåíòó. Ïåðåòèíè 11
³ 22 íåáåçïå÷í³. ʳíöåâà áàëêà ñ
ïðèéìຠçóñèëëÿ, ùî ä³þòü íå
ò³ëüêè ó âåðòèêàëüí³é, àëå é ó ãîðèçîíòàëüí³é ïëîùèí³.
Ðèñ. 25.6. Ñõåìà ê³íöåâî¿ áàëêè ìîñòà ñóö³ëüíîñò³ííî¿ êîíñòðóêö³¿ â³ä
ñèëè ³íåðö³¿
ã.ô
a
2 ,
2
G
P a
Rp
I
⋅
⎛⎞
=+−
⎜⎟
⎝⎠
S1 ³íåðö³éí³ ñèëè â³ä ïîñò³éíîãî íàâàíòàæåííÿ (áåðåìî ç
ä³àãðàìè ÌàêñâåëëàÊðåìîíè) äëÿ âåðõíüî¿ ãàëüì³âíî¿ ôåðìè.
S2 ³íåðö³éí³ ñèëè â³ä ðóõîìîãî íàâàíòàæåííÿ (âèçíà÷àºòüñÿ
ùîäî Ë.Â.).
Ñèëè S1, S2 âèíèêàþò
ü ó ãîðèçîíòàëüí³é ïëîùèí³ ïðè ãàëüìó-
âàíí³ ³ ïóñêó â³ä âëàñíèõ ìàñ êðàíà ³ â³çêà ç âàíòàæåì.
max
çã
Ì
ìàêñèìàëüíèé çãèíàëüíèé ìîìåíò, âèíèêàþ÷èé ó ãî-
ðèçîíòàëüí³é ïëîùèí³ ïðè ïóñêó ³ ãàëüìóâàíí³ â³ä ðóõîìîãî íàâàí-
òàæåííÿ.
Fí ïëîùà íåòòî åëåìåíòà, ùî ðîçðàõîâóºòüñÿ.
max
çã
Ì
ìàêñèìàëüíå çíà÷åííÿ çãèíàëüíîãî ìîìåíòó â íàï³â-
ïàíåë³, ÿêèé 䳺 ó âåðòèêàëüí³é ïëîùèí³ íà ñòðèæåíü, ùî ðîçðà-
õîâóºòüñÿ, ó ïðèïóùåíí³ óñòàíîâêè õîäîâîãî êîëåñà íàâàíòàæåíî-
ãî â³çêà â ñåðåä
í³é ÷àñòèí³ íàï³âïàíåë³.
Wx.
íåòòî
ìîìåíò îïîðó íåòòî ïåðåòèíó, ùî ðîçðàõîâóºòüñÿ,
ùîäî îñ³ x.
F
áðóòòî
ïëîùà áðóòòî åëåìåíòà, ùî ðîçðàõîâóºòüñÿ.
x
ϕ
êîåô³ö³ºíò çìåíøåííÿ íàïðóãè, ùî äîïóñêàºòüñÿ; âðàõî-
âóº âïëèâ ïîçäîâæíüîãî âèãèíó, ùî º ôóíêö³ºþ ãíó÷êîñò³ ñòðèæíÿ,
ùî ðîçðàõîâóºòüñÿ.
Wx
áð
ìîìåíò îïîðó áðóòòî ùîäî îñ³ x.
Íîðìè äîçâîëÿþòü ââîäèòè â ðîçðàõóíîê ïëîùó ïåðåòèíó ðåé-
êè ò³ëüêè ïðè âèçíà÷åíí³ íàïðóæåíü â³ä M
çã
, ÿêùî ðåéêà ïðèâàðå-
íà ïåðåðèâ÷àñòèì øâîì. ßêùî ðåéêà ïðèâàðåíà ñóö³ëüíèì ïî-
äîâæí³ì øâîì, òîä³ ìîæíà âðàõîâóâàòè ïëîùó ðåéêè ³ ïðè âèçíà-
÷åíí³ íàïðóæåíü â³ä ñòèñêàëüíîãî íàâàíòàæåííÿ.
25.3. Âèçíà÷åííÿ ñèë ³íåðö³¿, ùî âèíèêàþòü ïðè ïóñêó
³ ãàëüìóâàíí³ êðàíà
Âåëè÷èíà ñèëè ³íåðö³¿ ïðè ïóñêó ³ ãàëüìóâàíí³ îáìåæóºòüñÿ
ñèëîþ ç÷åïëåííÿ õîäîâîãî êîëåñà ç ðåéêîþ ³ íå ìîæå ïåðåâèùóâà-
òè äëÿ
0
1
;
2
n
n
=
()
òåë êð
0,1 ,
I Q GG
=⋅+ +
äå n0 ÷èñëî ïðèâîäíèõ
õîäîâèõ êîë³ñ, n çàãàëüíå ÷èñëî êîë³ñ.
ßêùî
0
1
n
n
=
òî
()
òåë êð
0, 2 .
I Q GG
=⋅+ +
Êð³ì òîãî, çã³äíî ç ïðà-
âèëàìè Äåðæíàãëÿäîõîðîíïðàö³ ìåæîâà âåëè÷èíà ñèëè ³íåðö³¿ â³çêà,
ùî ðóõàºòüñÿ ç âàíòàæåì óçäîâæ ìîñòà êðàíà
()
â³ç
1
.
7
I Q G
=⋅ +
Öÿ
ñèëà ñïðÿìîâàíà óçäîâæ ïðîëüîòó ìîñòà êðàíà.
G
=
R
A
Åïþðà
Ì
çãí
I
2
I
2
òð³ù³íè
G
=
R
A
G
=
R
A
G
=
R
A
250 251Î. Â. Ãðèãîðîâ, Í. Î. Ïåòðåíêî Âàíòàæîï³äéîìí³ ìàøèíè
Ñèëè ³íåðö³¿ ñïðèéìàþòüñÿ ò³ëüêè îäí³ºþ ê³íöåâîþ áàëêîþ.
Ðåêîìåíäîâàíî óñ³ âåðòèêàëüí³ íàâàíòàæåííÿ íà êðåñëåíí³ áàëêè
çîáðàæóâàòè çá³ëüøåíèìè íà 20% ç ìåòîþ óðàõóâàííÿ äîäàòêîâèõ
íàâàíòàæåíü (ïåðåêîñó). Ç ò³ºþ æå ìåòîþ Äåðæíàãëÿä
îõîðîíïðàö³
ïåðåäáà÷ຠçíèæåííÿ
[]
σ
äî 80ÌÏà äëÿ ñòàë³ Ñò 3.
25.5. Ìàãí³òíà ä³àãíîñòèêà òà êîíòðîëü îñòàòî÷íîãî ðåñóðñó
ìåòàëîêîíñòðóêö³é ï³äéîìíèõ ñïîðóä [1]
Ìàþ÷è íà óâàç³ ïðîáëåìó ñòàð³ííÿ óñòàòêóâàííÿ, ôàõ³âö³ Ðîñ³¿
òà Óêðà¿íè, îáºäíàâøè ñâî¿ çóñèëëÿ, ïðîâåëè âåëèêèé îáñÿã íàó-
êîâèõ ³ ïðèêëàäíèõ äîñë³äæåíü, ðåçóëüòàòîì ÿêèõ ñòàëà ðîçðîáêà
àïàðàòóðè ³ ìåòîä
èêè ìàãí³òíî¿ ä³àãíîñòèêè ìåõàí³÷íèõ âëàñòèâî-
ñòåé ³ çàëèøêîâîãî ðåñóðñó ìåòàëîêîíñòðóêö³é ï³äéîìíèõ êðàí³â,
êðàíîâèõ øëÿõ³â, ë³ôò³â òà ³íøîãî óñòàòêóâàííÿ ç ìàëîâóãëåöåâèõ
êîíñòðóêö³éíèõ ñòàëåé. Äîñë³äæåííÿ ç ìàãí³òíî¿
ä³àãíîñòèêè îäå-
ðæàëè âèçíàííÿ íà ºâðîïåéñüêèõ ³ ñâ³òîâèõ êîíôåðåíö³ÿõ íåðóéí³-
âíîãî êîíòðîëþ ó Êîïåíãàãåí³ ³ Ðèì³.
Íîðìàòèâíîþ áàçîþ ìàãí³òíîãî êîíòðîëþ (ÌÊ) ìåòàëîêîíñ-
òðóêö³é ç ìàëîâóãëåöåâèõ
ñòàëåé º ̳æäåðæàâíèé ñòàíäàðò ÄÑÒ
30415, ñòàíäàðò ²ÑÎ 4301 ³ ìåòîäè÷í³ âêàç³âêè ÐÄ ²ÊÖ «ÊÐÀÍ»
007-97 «Ìàãí³òíèé êîíòðîëü íàïðóæåíî-äåôîðìîâàíîãî ñòàíó
³ çàëèøêîâîãî ðåñóðñó ï³äéîìíèõ ñïîðóäæåíü ïðè ïðîâåäåíí³ ¿õ-
íüîãî îáñòåæåííÿ ³ òåõí³÷íîãî ä³àãíîñòóâàííÿ» (óçãîäæåí³ ç Äåðæ-
òåõíàãëÿäîì Ðîñ³¿ 27.11.97 ð. ¹ 12-7/1113).
Àïàðàòóðíå çàáåçïå÷åííÿ ìàãí³òí³ ñòðóêòóðîñêîïè ñåð³¿
ÊÐÌ-ÖÊ-2Ì òà ÇÌ, ùî âèïóñêàþòüñÿ Õàðê³âñüêî
þ ÍÏÔ «Ñïåö³-
àëüí³ íàóêîâ³ ðîçðîáêè» ðàçîì ³ç ÌÍÏÎ «Ñïåêòð» (Ìîñêâà).
Åêñïåðèìåíòàëüí³ ðîáîòè ôàõ³âö³â ÇÀÒ ²ÊÖ «Êðàí» (Ìîñêâà),
õàðê³âñüêèõ ïðèëàäîáóä³âíèê³â ³ òåîðåòè÷íå îáãðóíòóâàííÿ â÷åíèõ
ÓðÎ Ð
ÀÍ (ªêàòåðèíáóðã) äîçâîëèëè ñòâîðèòè íàóêîâî-òåõí³÷íó
áàçó íîâîãî ìåòîäó íà îñíîâ³ êîíòðîëþ îñíîâíîãî ìàãí³òíîãî
ïàðàìåòðà ôåðîìàãí³òíîãî ìàòåð³àëó êîåðöèòèâíî¿ ñèëè Íc.
 îñíîâó ìåòîäèêè ïîêëàäåí³ êîðåëÿö³éí³ çàëåæíîñò³ ì³æ ô³çèêî-
ìåõàí³
÷íèìè âëàñòèâîñòÿìè ìåòàëó ³ ïàðàìåòðîì ïåòë³ ìàãí³òíîãî
ã³ñòåðåç³ñó (Íc), êîíòðîëüîâàíèì ïðè ñòàòè÷íèõ ³ ñòàëèõ âèïðîáó-
âàííÿõ íà âñ³õ ñòàä³ÿõ íàïðóæåííÿ àæ äî ðóéíóâàííÿ. ³äïîâ³äíî
äî òåî𳿠ª.².Êîíäîðñüêîã
î ³ñíóº ïðÿìèé çâÿçîê ì³æ âíóòð³øí³ìè
íàïðóæåííÿìè (
ÂÍ
σ
), äåôîðìàö³ºþ (
S
λ
) ³ íåîáîðîòíèì íàìàãí³÷ó-
âàííÿì, õàðàêòåðíèì êîåðöèòèâíîþ ñèëîþ Íc:
G
á.ô
çâåäåíà âàãà á³÷íî¿ ôåðìè;
G
ã.ô
çâåäåíà âàãà ãîëîâíî¿ ôåðìè.
Åïþðà çãèíàëüíîãî ìîìåíòó â³ä ñèë ³íåðö³¿, ùî ä³þòü íà ê³íöå-
âó áàëêó â ãîðèçîíòàëüí³é ïëîùèí³, çîáðàæåíà íà ðèñ. 25.7.
Ðèñ. 25.7. Ñõåìà ê³íöåâî¿ áàëêè ìîñòà ðåø³ò÷àñòî¿ êîíñòðóêö³¿
Ðèñ. 25.8. Åïþðà çãèíàëüíîãî ìîìåíòó, ä³þ÷îãî íà ê³íöåâó áàëêó ó ãîð³çîíòà-
ëüí³é ïëîùèí³
2
2
²
²
Á
R
À
G
¢
á.ô.
R
À
G
¢
á.ô.
Åïþðà
Ì
çã
K
1
K
1
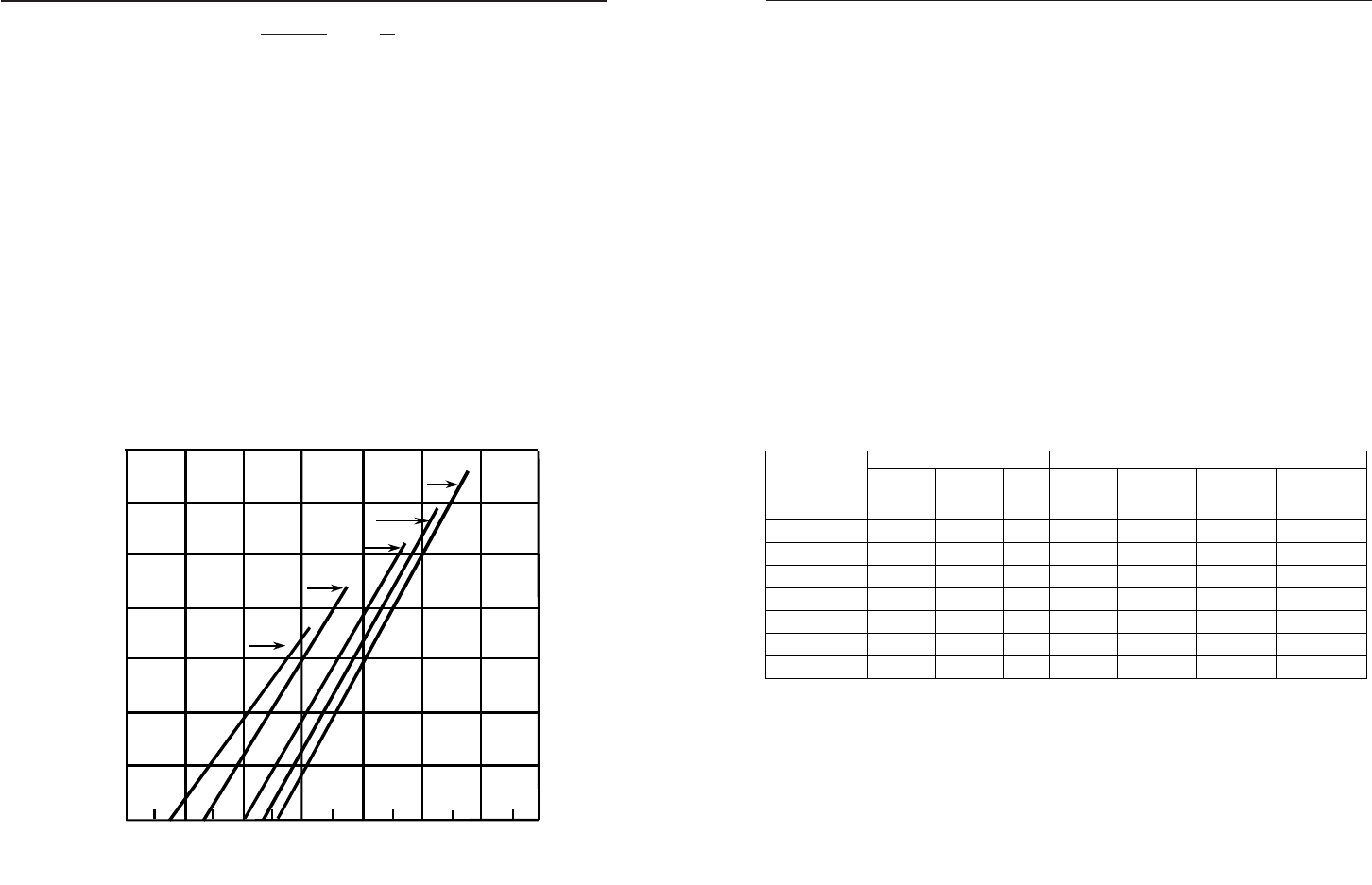
252 253Î. Â. Ãðèãîðîâ, Í. Î. Ïåòðåíêî Âàíòàæîï³äéîìí³ ìàøèíè
Òàê³ íîìîãðàìè äîçâîëÿþòü âèð³øóâàòè çâîðîòí³ çàäà÷³
òîáòî âèçíà÷àòè ð³âåíü ä³þ÷èõ ÷è çàëèøêîâèõ íàïðóæåíü ó êîíñ-
òðóêö³¿ çà äàíèìè êîíòðîëþ âåëè÷èíè êîåðöèòèâíî¿ ñèëè. À ï³ñëÿ
ïîáóäîâè ä
³àãðàì íàâàíòàæåííÿ ç êîíòðîëåì Íc ó ïðóæí³é ³ ïëà-
ñòè÷í³é îáëàñòÿõ çÿâëÿºòüñÿ ìîæëèâ³ñòü óñòàíîâèòè áàçîâ³ ìàãí³-
òí³ ïàðàìåòðè êîíòðîëþ çà ñòàíîì ìåòàëó ùîäî âåëè÷èíè êîåðöè-
òèâíî¿ ñèëè, ÿêà â³äïîâ³äຠòðàäèö³
éíèì ìåõàí³÷íèì âëàñòèâîñòÿì:
Íñ° âèõ³äíå çíà÷åííÿ êîåðöèòèâíî¿ ñèëè (ì³í³ìàëüíå ï³ñëÿ
â³äïàëó), Hc â³äïîâ³äຠð³âíþ âíóòð³øí³õ íàïðóæåíü, ùî äî-
ð³âíþþòü ô³çè÷í³é ãðàíèö³ òåêó÷îñò³ ñòàë³
T
σ
(
0,2
σ
),
B
c
H
â³äïî-
â³äຠäîñÿãíåííþ ìåæ³ ì³öíîñò³ ñòàë³
B
σ
, Íñ ÷è
ÓÑÒ
c
H
â³äïîâ³-
äຠìåæ³ âèòðèâàëîñò³ ïðè ìàëîöèêëîâ³é óòîì³ (ÌÖÓ) ïðè ïóëüñó-
þ÷îìó öèêë³ íàâàíòàæåííÿ.
Óçàãàëüíåí³ äàí³ ìàãí³òíèõ ³ ìåõàí³÷íèõ âëàñòèâîñòåé äëÿ òðà-
äèö³éíèõ íèçüêîëåãîâàíèõ ³ ìàëîâóãëåöåâèõ
ñòàëåé ïðåäñòàâëåí³
â òàáë. 25.1.
Òàáëèöÿ 25.1
Ìàãí³òí³ ³ ìåõàí³÷í³ âëàñòèâîñò³ äëÿ ñòàëåé
Ìåõàí³÷í³ âëàñòèâîñò³ Ìàãí³òí³ âëàñòèâîñò³
Íc
, à/ñì
Ìàðêà ñòàë³
B
s
,
êã/ìì
2
0,2
s
,
êã/ìì
2
d
,
%
0
c
H
T
c
H
B
c
H
ÓÑÒ
c
H
Ñò3 35 21 22 2,5 5 6 5,8
ÂÑò3ñï 40 24 25 3 5,5 6,5 5,9
09Ã2Ñ 45 31 20 4 7,8 9,5 9,5
10ÕÑÍÄ 54 40 19 5 11,5 14,5 13,5
ÑÒ20 42 26 24 4,5 10,5 13,5 13
Ñò «Äñ» 6065 3540 15 56 88,5 1011 9,510,5
17Ã1Ñ 52 35 23 4 10 14 14
Õàðàêòåðíî, ùî â³äïîâ³äíî äî åíåðãåòè÷íî¿ òåî𳿠ìàêñèìàëü-
í³ êðèòè÷í³ çíà÷åííÿ êîåðöèòèâíî¿ ñèëè äëÿ êîæíî¿ ìàðêè ñòàë³,
ùî â³äïîâ³äàþòü ìåæ³ ì³öíîñò³ ³ ìåæ³ óòîìè ïðè ÌÖÓ, çá³ãàþòüñÿ.
Òîáòî,
êîæíà ìàðêà ñòàë³ ìຠâèçíà÷åíèé çàïàñ ìàãí³òíî¿ åíåð㳿,
âè÷åðïàííÿ ÿêîãî, íåçàëåæíî â³ä âèäó íàâàíòàæåííÿ, ñóïðîâîäæó-
ºòüñÿ ïåðåõîäîì ó ñòàä³þ ðóéíóâàííÿ ìåòàëó ïðè
max B
cc
.
HH=
Öå
ïðèíöèïîâà â³äì³íí³ñòü ìàãí³òíî¿ ñòðóêòóðîñêîﳿ â³ä ³íøèõ ìåòî-
ä³â, ÿê³ íå ðóéíóþòü, äîçâîëÿº óâîäèòè ô³çè÷íî îá´ðóíòîâàí³ êðè-
òå𳿠ïåðåõîäó ìåòàëó â ïëàñòè÷íèé ñòàí
T
c
H
³ âñòàíîâëþâàòè ãðà-
íè÷íèé ñòàí, ùî â³äïîâ³äຠâè÷åðïàííþ çàïàñó ïëàñòè÷íîñò³ ñòà-
c ÂÍ
,
S
SS
H
M L
λ
δ
∆= ∆σ
µ⋅
äå
ÂÍ
∆σ
ñåðåäí³ çíà÷åííÿ àìïë³òóäè âíóòð³øí³õ íàïðóæåíü,
S
λ
çì³íà ë³í³éíèõ ðîçì³ð³â ìàãí³òîñòðèêö³ÿ,
S
µ
àáñîëþòíà ìà-
ãí³òíà ïðîíèêí³ñòü, ÌS íàìàãí³÷åí³ñòü,
δ
òîâùèíà ãðàíèö³
äîìåí³â, L äîâæèíà õâèë³ íàïðóãè â ìåòàë³.
Êîåðöèòèâíà ñèëà Íc º á³ëüø ³íôîðìàòèâíèì ïàðàìåòðîì,
òîìó ùî âèçíà÷àºòüñÿ òîíêîþ ñòðóêòóðîþ ìåòàëó ³ çâÿçàíà ç ìà-
ãí³òíîþ åíåð㳺þ ³ âíóòð³øí³ì ïîëåì àí³çîòðîﳿ, ð³çíèìè äëÿ êî-
æíîãî òèïó ñòàë³. Òîìó ºäí³ñòü ïðèðîäè íàìàãí³÷óâàííÿ ìåòàëó ç
ðîñòîì ïðóæíèõ-ïëàñòè÷íèõ äåôîðìàö³é ³ âíóòð³øí³õ íàïðóæåíü,
ùî ïðèâîäèòü äî ï³äâèùåííÿ çíà÷åí
ü êîåðöèòèâíî¿ ñèëè â 23
ðàçè â ïîð³âíÿíí³ ç âèõ³äíèì, äîçâîëÿº ìîäåëþâàòè íà çðàçêàõ
ïðîöåñ íàâàíòàæåííÿ ìåòàëó ïðè åêñïëóàòàö³¿ çà óìîâ ñêëàäíî-íà-
âàíòàæåíîãî ñòàíó. Íà ðèñ. 25.9 ó âèä³ ñòàòèñòè÷íî îáðîáëåíè
õ
íîìîãðàì ïðåäñòàâëåí³ çàëåæíîñò³ Íc â³ä ä³þ÷î¿ íàïðóãè ïðè ñòà-
òè÷íîìó ðîçòÿãàíí³ ïëîñêèõ çðàçê³â ç êîíñòðóêö³éíèõ ñòàëåé ÑòÇ,
ÂÑòÇñï, 09Ã2Ñ, 17Ã1Ñ òà ³í.
Ðèñ. 25.9. Íîìîãðàìè äëÿ êîíòðîëþ ùîäî êîåðöèòèâíî¿ ñèëè íàïðóæåí-
íÿ â êîíñòðóêö³ÿõ ³ç ñòàëåé: Ñò3; ÂÑò3ñï; Äñ
Çíà÷åííÿ êîåðöèòèâíî¿ ñèëè ìåòàëó,
Í
Ñ
,
À/ñì
Âåëè÷èíà íàïðóæåííÿ
s
, ÌÏà
ÌÏà
,
s
600
500
400
300
200
100
0
2
4
6
8
10
12
ÀÍ
Ñ
,
3
Ñò
ñïÂÑò
3
ÑÃ
209
ÑÃ
117
Äñ
σ, ÌÏà
254 255Î. Â. Ãðèãîðîâ, Í. Î. Ïåòðåíêî Âàíòàæîï³äéîìí³ ìàøèíè
×
àñòîòà çÿâëåííÿ çíà÷åíü
êîåðöèòèâíî¿ ñèëè
j
Ï
Çíà÷åííÿ êîåðöèòèâíî¿ ñèëè ìåòàëó, ùî êîíòðîëþýòüñÿ
Íñ
, À/ñì
Ï
j
150
100
50
0
3
4
5
6
7
8
9
Ñ
Í
10
êðèòè÷íèé
êîíòðîëþþ÷èé
íàä³éíèé
Ðåæèì åêñïëóàòàö³¿
53
ñïÂÑò ÑÃ
209
Äñ
• ðåæèì íàä³éíî¿ åêñïëóàòàö³¿ (
max T
cc
HH<<
) (I)
• ðåæèì êîíòðîëüîâàíî¿ åêñïëóàòàö³¿ (
max T
cc
HHJ
) (II)
• êðèòè÷íèé ðåæèìó-åêñïëóàòàö³¿ (
B max T
cc c
HH HII
) (III)
Ó êðèòè÷íîìó ðåæèì³ åêñïëóàòàö³¿ îêðåì³ åëåìåíòè ÏÑ ïðàöþ-
þòü ó ïðóæíî-ïëàñòè÷í³é ³ ïëàñòè÷í³é îáëàñòÿõ ä³àãðàìè íàâàíòà-
æåííÿ. Ïðè öüîìó â ê³ëüêà ðàç³â çðîñòຠòåõí³÷íèé ðèçèê ðóéíó-
âàííÿ, à
â ì³ñöÿõ êîíöåíòðàö³¿ íàïðóãè óòâîðþþòüñÿ òð³ùèíè, äå
ìຠì³ñöå íàäíîðìàòèâíà ïëàñòè÷íà äåôîðìàö³ÿ.
Ñòàòèñòè÷íèé àíàë³ç çà ðåçóëüòàòàìè îáñòåæåííÿ á³ëüø, í³æ
3000 ï³äéîìíèõ êðàí³â óñ³õ òèï³â ³
ë³ôò³â, ïîêàçàâ, ùî ï³ñëÿ 30
ðîê³â åêñïëóàòàö³¿ ìåòàëîêîíñòðóêö³¿ ÏÑ íà 60% ïðàöþþòü ó ðå-
æèì³ íàä³éíî¿ åêñïëóàòàö³¿, ïðèáëèçíî 25% ó ðåæèì³ êîíòðî-
ëüîâàíî¿ åêñïëóàòàö³¿ ³ áëèçüêî 5% ó êðèòè÷íîìó ðåæèì³ (ðèñ.
25.11). Ïðè öüîìó 1,52% ï³äí³ìàëüíèõ ñïîðóäæåíü ìàþòü îêðåì³
íåñó÷³ åëåìåíòè êîíñòðóêö³¿, ùî âè÷åðïàëè çàïàñ ïëàñòè÷íîñò³ ³ íå
çäàòí³ âèòðèìàòè ðîçðàõóíêîâ³ íàâàíòàæåííÿ.
˳òåðàòóðà
1. Ïîäúåìíûå ñîðóæåíèÿ. //Ñïåöèàëüíàÿ òå
õíèêà. ¹ 7. 2002,
Ñ. 2526.
Ðèñ. 25.11. Ðîçïîä³ë Íc â òîíêîñò³ííèõ êîíñòðóêö³ÿõ ï³ñëÿ 30 ðîê³â
åêñïëóàòàö³¿
ë³ ³ ïåðåõîäó ¿¿ â ñòàä³þ çíåì³öíåííÿ (
B
c
H
àáî
c
N
H
). Òàê³ êðèòåð³¿
îö³íêè íàïðóæåíî-äåôîðìîâàíîãî ñòàíó ïðè öèêë³÷íîìó íàâàíòà-
æåíí³ ëÿãëè â îñíîâó ìåòîäó êîíòðîëþ çàëèøêîâîãî ðåñóðñó ÿê
îêðåìèõ íåñó÷èõ åëåìåíò³â ï³äí³ìàëüíèõ ñïîðóäæåíü, òàê ³ âñ³º¿
ìåòàëîêîíñòðóêö³¿ â ö³ëîìó.
³äïîâ³äíî äî ÄÑÒ 27.002-89 «Íàä³éí³ñòü ó òåõí³ö³» çàëèøêî-
âèé ðåñóðñ öå ñóìàðíèé íàðîá³òîê îáºêòà â³ä ìîìåíòó êîíòðî-
ëþ äî ïåðåõîäó â ãðàíè÷íèé ñòàí. Çàëèøêîâèé ðåñóðñ ìîæå áóòè
âèðàæåíèé ó ö
èêëàõ, ãîäèíàõ ³ â³äñîòêàõ. Äëÿ âèçíà÷åííÿ ãðàíè÷-
íîãî ñòàíó áóëè ïðîâåäåí³ öèêë³÷í³ ³ñïèòè ñòàëåé ïðè íàâàíòàæåí-
íÿõ, ùî ìîäåëþþòü ëåãêèé, ñåðåäí³é ³ âàæêèé ðåæèìè ðîáîòè ÏÑ
çà êëàñèô³êàö³ºþ ²S
Î 4301 1Ê-8Ê. ϳñëÿ ñòàòèñòè÷íî¿ îáðîáêè çà-
ëåæíîñòåé Íñ-l ó äîâ³ð÷îìó ³íòåðâàë³ 0,95 áóëè ïîáóäîâàí³ íîìî-
ãðàìè äëÿ êîíòðîëþ çàëèøêîâîãî ðåñóðñó çà âåëè÷èíîþ ìàêñèìàëü-
íî¿ êîåðöèòèâíî¿ ñèëè ³ âñòàíîâëåí³ ðåæèìè åêñïëóàòàö³¿ ÏÑ çàëåæ-
íî â³ä ñòðóêòóðíîãî ñòàíó ìåòàëó (ðèñ. 25.10):
Ðèñ. 25.10. Íîìîãðàìè äëÿ ìàãí³òíîãî êîíòðîëþ çàëèøêîâîãî ðåñóðñó
ìåòàëîêîíñòðóêö³é ï³äí³ìàëüíèõ ñïîðóäæåíü çà ISO 4301
5
.
10
5
.
10
N, öèêëîâ
Ðåñóðñ ìåòàëîêîíñòðóêö³¿ â öèêëàõ
Ðåñóðñ ìåòàëîêîíñòðóêö³¿ â óìîâíèõ çì³íàõ
Ðåñóðñ ìåòàëîêîíñòðóêö³¿ â %
40
Ìàêñèìàëüíå çíà÷åííÿ Íc (A/ñì)
Ðåæèì
êîíòîëüîâàíî¿
åêñïëóàòàö³¿
2 4
Êðèòè÷íèé ðåæèì
åêñïëóàòàö³¿
4
68
10
0
10
20
30
500
1000
6
10
10
5
5
Ðåæèì íàä³éíî¿
åêñïëóàòàö³¿
Ðåæèì Q1
Ðåæèì Q3
Ðåæèì Q3
Ðåæèì Q1
09Ã2Ñ
ÂÑò3ñï
60
1500
2000
80
2500
3000
C, çì³í
P,%
3500
êîíòðîëüîâàíî¿
N
P
C

257Âàíòàæîï³äéîìí³ ìàøèíè
ä) êàçàí äëÿ âîäè ïîðîæí³é àáî ïîðîæí³é áàê äëÿ äèçåëüíîãî
ïàëèâà.
3-å ðîçðàõóíêîâå ïîëîæåííÿ â³äïîâ³äຠðîçòàøóâàííþ êðàíà íà
ðîáî÷³é ïëîùàäö³ ç íàéá³ëüøèì ïðè
ïóñòèìèì íàõèëîì ó á³ê ïåðå-
êèäàííÿ êðàíà;
á) ñòð³ëà ç âàíòàæåì íà íàéá³ëüøîìó âèëüîò³ ñïðÿìîâàíà â ïëà-
í³ ï³ä êóòîì 45° äî íàïðÿìêó ðåáðà ïåðåêèäàííÿ ó á³ê íàõèëó ðî-
áî÷î¿ ïëîùàäêè. Í
à êðàí êð³ì äîäàòêîâèõ íàâàíòàæåíü, ùî âðàõî-
âóþòüñÿ â ïåðøîìó ðîçðàõóíêîâîìó ïîëîæåíí³ ³ ñïðÿìîâàíèõ ïå-
ðïåíäèêóëÿðíî äî ðåáðà ïåðåêèäàííÿ, 䳺 äîòè÷íå ³íåðö³éíå
íàâàíòàæåííÿ â³ä ìàñè âàíòàæó ³ ñòð³ëè,
âèêëèêàíå ðîáîòîþ ìåõà-
í³çìó ïîâîðîòó êðàíà â íåñòàëîìó ðåæèì³.
Âåëè÷èíà êîåô³ö³ºíòà âàíòàæíî¿ ñò³éêîñò³ Ê äëÿ ïåðøîãî ³ òðå-
òüîãî ïîëîæåíü íå ïîâèííà áóòè ìåíøå 1,15.
4-å ðîçðàõóíêîâå ïîëî
æåííÿ âàíòàæíî¿ ñò³éêîñò³ â³äïîâ³äຠðîç-
òàøóâàííþ êðàíà íà ãîðèçîíòàëüí³é ïëîùàäö³. Âðàõîâóþòüñÿ ò³ëü-
êè îñíîâí³ íàâàíòàæåííÿ â³ä âàíòàæó ³ âàãè êðàíà. Äîäàòêîâ³ íàâàí-
òàæåííÿ (â³òåð, ³íåðö³ÿ) íå âðàõîâóþòüñÿ,
ïðè öüîìó
1, 4K
I
. Ó âñ³õ
³íøèõ ïîëîæåííÿõ
1,5K
I
.
Ïåðåâ³ðêà âëàñíî¿ ñò³éêîñò³ êðàíà áåç âàíòàæó â íåðîáî÷îìó
ïîëîæåíí³ ïåðåâ³ðÿºòüñÿ êîåô³ö³ºíòîì âëàñíî¿ ñò³éêîñò³, ïðè öüî-
ìó ïåðåäáà÷àºòüñÿ íàñòóïíå:
• Êðàí íà ïîõ
èëîìó øëÿõó ç êóòîì íàõèëó α ³ ñâîºþ ì³í³ìàëü-
íîþ áàçîþ çâåðíåíèé ó á³ê íàõèëó øëÿõó.
• Ñòð³ëà ï³äíÿòà â êðàéíº âåðõíº ïîëîæåííÿ, à êðàí ìຠáóòè
ðîçâàíòàæåíèì.
• Íà êðàí ó á³ê éîãî ïåðåêèäàííÿ ä³þòü â³òðîâ³
íàâàíòàæåííÿ
íåðîáî÷îãî ñòàíó.
• Êàçàí íà ïàðîâîìó êðàí³ ìຠáóòè çàïîâíåíèé ö³ëêîì âîäîþ,
íà äèçåëüíîìó çàïîâíåíèé ïàëèâíèé áàê.
Êîåô³ö³ºíò âàíòàæíî¿ ñò³éêîñò³ äëÿ 1-ãî ðîçðàõóíêîâîãî ïîëî-
æåííÿ:
1,15,
()
iA
M
Q a l
β=
−
∑
I
äå
6
(cos sin ...).
iA nn
MG cG h
=α⋅+⋅α⋅+
∑
Ïðè ðîçðàõóíêó êîåô³ö³ºíòà âàíòàæíî¿ ñò³éêîñò³ çà 3-ì ðîçðà-
õóíêîâèì ïîëîæåííÿì (áåç îáë³êó äîäàòêîâèõ ñèë ³íåðö³¿ ³ â³òðó)
()
1, 4.
()
i A
M
Q a l
β=
−
∑
I
Ðîçä³ë 26
ÑÒ²ÉʲÑÒÜ ÏÅÐÅÑÓÂÍÈÕ ÊÐÀͲÂ
Ïðàâèëàìè Äåðæíàãëÿäîõîðîíïðàö³ ïåðåäáà÷åíà ïåðåâ³ðêà
âàíòàæíî¿ ñò³éêîñò³ äëÿ 4 ïîëîæåíü êðàíà ³ ïåðåâ³ðêà éîãî âëàñíî¿
ñò³éêîñò³.
Ïåðåâ³ðêà âàíòàæíî¿ ñò³éêîñò³ âêëþ÷ຠ4 ïîëîæåííÿ êðàíà:
1-å ðîçðàõóíêîâå ïîëîæåííÿ â³äïîâ³
äຠíàñòóïíîìó:
à) êðàí ðîçòàøîâàíèé íà ðîáî÷³é ïëîù³ (øëÿõó) ç íàõèëîì
α°
(
3
α= °
ïðè ðîáîò³ áåç àóòðèãåð³â,
1,5α= °
ïðè ðîáîò³ ç
àóòðèãåðàìè) ³ ñâîºþ íàéìåíøîþ áàçîþ çâåðíåíèé ó á³ê íàõèëó
øëÿõó;
á) ïåðåäáà÷àºòüñÿ, ùî êðàí íàâàíòàæåíèé íîì³íàëüíèì âàíòà-
æåì, à ñòð³ëè îïóùåí³ â êðàéíº íèæíº ïîëîæåííÿ;
â)
ïåðåäáà÷àºòüñÿ, ùî çä³éñíþþòüñÿ ñïîëó÷åí³ îïåðàö³¿: ïîâî-
ðîòó êðàíà, îïóñêàííÿ âàíòàæó ç ãàëüìóâàííÿì ³ çì³íîþ âèëüîòó
ñòð³ëè (ÿêùî öå ïðèïóñòèìî ³íñòðóêö³ºþ ç åêñïëóàòàö³¿). Ïðè ö
üî-
ìó çíà÷åííÿ øâèäêîñò³ îïóñêàííÿ âàíòàæó
0
V
ïðèéìàºòüñÿ òàêå,
ùî äîð³âíþº 1,5 øâèäêîñò³ ï³äéîìó, òîáòî
0 ï³äéîìó
1,5
VV=⋅
. ßêùî
êðàí îáëàäíàíèé ðåâåðñíîþ ëåá³äêîþ, òî
0
VV=
. Âàíòàæ îïóñêà-
ºòüñÿ ³ ãàëüìóºòüñÿ. ×àñ ãàëüìóâàííÿ ïðèáëèçíî äîð³âíþº 0,5 ñ;
ã) ïåðåäáà÷àºòüñÿ, ùî ó á³ê ïåðåêèäàííÿ êðàíà ä³þòü â³òðîâ³
íàâàíòàæåííÿ ðîáî÷îãî ñòàíó ç ³íòåíñèâí³ñòþ
250p =
Í/ì
2
;
ä) ââàæàºìî, ùî êàçàí äëÿ âîäè (ïðîòèâàãà ïàðîâèõ êðàí³â) ÷è
áàê äëÿ ïàëèâà ñïîðîæíåí³;
2-å ðîçðàõóíêîâå ïîëîæåííÿ âèçíà÷åííÿ çàïàñó âàíòàæíî¿
ñò³éêîñò³ äëÿ êðàíà, ùî ðóõàºòüñÿ.
Ð
îçðàõóíêîâ³ óìîâè äëÿ öüîãî ïîëîæåííÿ:
à) êðàí çíàõîäèòüñÿ íà ïîõèëîìó øëÿõó ³ íàéá³ëüøîþ áàçîþ
çâåðíåíèé ó á³ê óõèëó øëÿõó;
á) êðàí íàâàíòàæåíèé íîì³íàëüíèì âàíòàæåì ³ ñòð³ëà ç
íàõî-
äèòüñÿ â êðàéíüîìó íèæíüîìó ïîëîæåíí³;
â) íà êðàí ó á³ê éîãî ïåðåêèäàííÿ ä³þòü â³òðîâ³ íàâàíòàæåííÿ
ðîáî÷îãî ñòàíó;
ã) êðàí ðóõàºòüñÿ ó á³ê íàõèëó øëÿõó ç ìàêñèìàëüíîþ ðîçðàõóí-
êîâî
þ øâèäê³ñòþ é îäíî÷àñíî ïðîâîäèòü ìàêñèìàëüíî ³íòåíñèâ-
íå ãàëüìóâàííÿ.
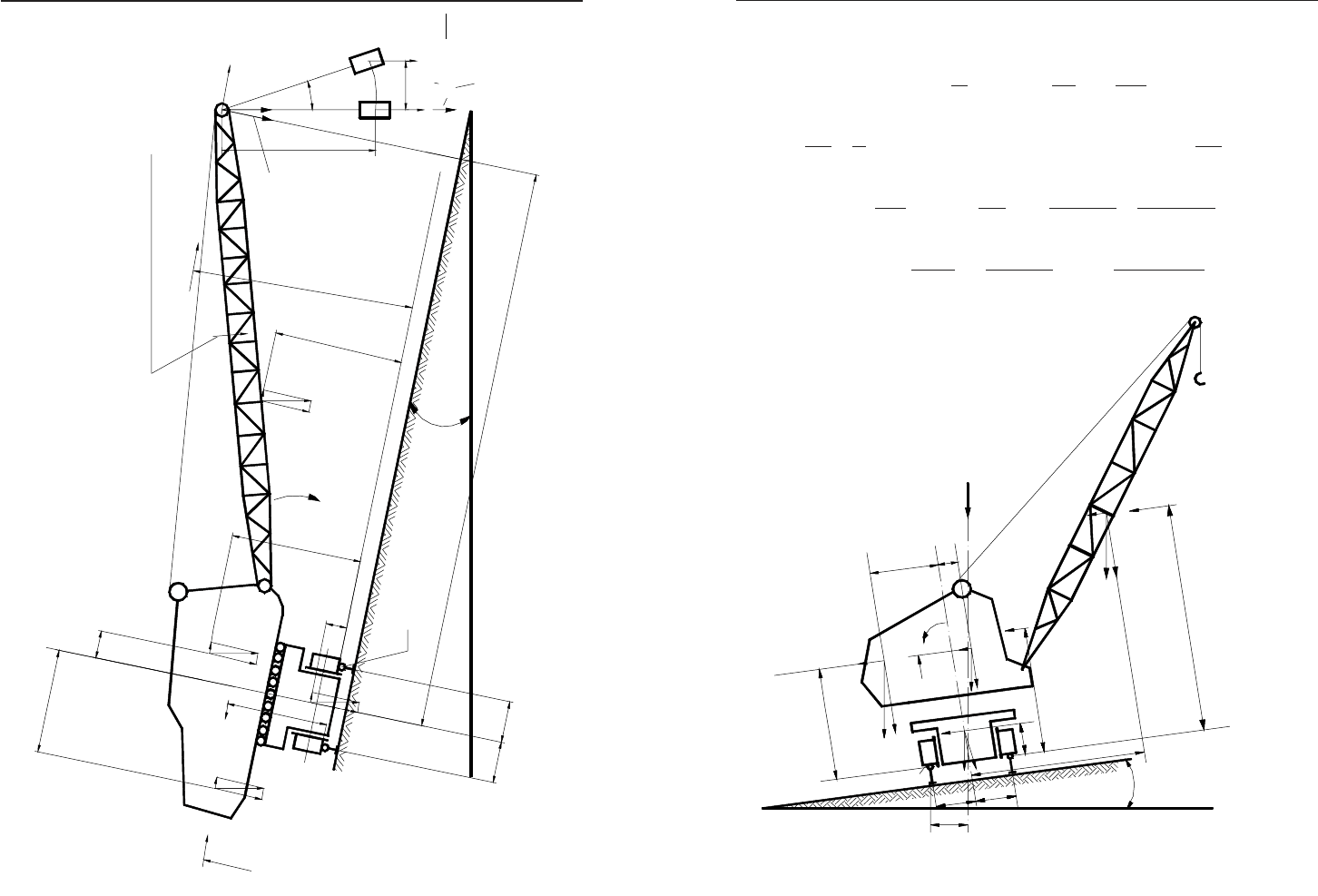
258 259Î. Â. Ãðèãîðîâ, Í. Î. Ïåòðåíêî Âàíòàæîï³äéîìí³ ìàøèíè
Íà ðèñ. 26.1 ïîçíà÷åí³: Ñ â³äöåíòðîâà ñèëà ³íåðö³¿; Ð
â
â³-
òðîâå íàâàíòàæåííÿ; G âàãîâ³ íàâàíòàæåííÿ; Q âàãà âàíòàæó.
2
22
() ();
30 900
Q
Q n Q
C m R a x nax
g
π
⎛⎞
=⋅⋅ω=⋅+⋅ = ⋅+
⎜⎟
⎝⎠
Q
C
x
Q y
=
(ïðè ó
J
40 ì òà n
J
3 îá/õâ);
;
Q
C
xy
Q
=⋅
2
2
2
,
900 900 900
QQ
Q
CCn y
QQna
C na y
Q
⋅⋅
⎛⎞
⋅⋅
=⋅+= +
⎜⎟
⎝⎠
22 2
2
1 ; .
900 900
900
QQ
n y Q na Q na
CC
n y
⎛⎞
⋅⋅⋅ ⋅⋅
⋅− = =
⎜⎟
−⋅
⎝⎠
G
c
f
G
k
×
cos
a
G
k
×
sin
a
G
n
h
4
B
G
m
h
3
h
2
b
h
5
a
P
âê
*
h
1
G
c
×
cos
a
P
â
c
*
å
v
d
c
G
c
×
sin
a
l
l
Ðèñ. 26.2. Ñõåìà äëÿ ïåðåâ³ðêè êîåô³ö³ºíòà âëàñíî¿ ñò³éêîñò³ êðàíà áåç
âàíòàæó ó íåðîáî÷îìó ïîëîæåíí³
Ðèñ. 26.1. Ñõåìà äëÿ âèçíà÷åííÿ êîåô³ö³ºíòà âàíòàæíî¿ ñò³éêîñò³ çà 1-ì ðîçðàõóíêîâèì ïîëîæåííÿì
Ñèëà ³íåðö³¿ ïðè ãàëüìóâàíí³
ìåõàí³çìà çì³íè âèëüîòó
×
cos
a
Íàïðÿì
ìîæëèâîãî
ïåðåêèä
àííÿ
êðàíó
C
G
h
òåë.
G
A
5
a
à
2
h
×
sin
a
×
sin
a
G
P
â
ê
ð
×
cos
a
G
ï
h
4
G
ï
ï
G
h
6
C
ï
k
G
k
d
C
h
3
G
C
1
h
C = Q
Äîäàòêîâà
âåðòèêàëüíà
ñèëà
Q
Q
x
×
V
ãð
ãàë
ü
t
Q
Q
×
cos
a
ñ
ò
ð
C
B
P
Q
y
d
Q
C
Q
l
l
ó
à
