Graziani F. (editor) Computational Methods in Transport

Подождите немного. Документ загружается.

346 R.M. Shagaliev et al.

II step: corrector – iterative:

s+1,ν+

∆ε

n+1

∆t

+ L

s+1,ν+

∆ε

n+γ

+α

∆

s+1,ν+

n+γ

−l



j=1

∆

s+1,ν+

n+γ

=(1− l)

2π



j=1

s+1,ν

∆ε

(0)n+γ

2π



j=1

∆ε

(0)n+γ

s+1,ν+

∆ε

s+1,ν+

−

s+1,ν

s+1,ν+1

∆

n+1

∆t

+ L

s+1,ν+1

∆

n+γ

+α

∆

s+1,ν+1

n+γ

−



j=1

∆

s+1,ν+1

n+γ

=(1− l)

2π



j=1

s+1,ν+

∆ε

(0)

n+γ

−(1 − l)

2π



j=1

,ν

∆ε

(0)

n+γ

s+1,ν+1

∆

s+1,ν+1

∆ε

−

s+1,ν+

∆ε

Numerical studies of the KM3 method

Benchmark problem «Tube»:

Region 2 (10×100)

Region 1 (10×100)

1.2

Fig. 15. Problem geometry

The number of iterations in region 2 (NIter

= 1, l = const = 0.5)

∆t =0.1 · 10

−10

sec ∆t =0.5 · 10

−10

sec ∆t =0.1 · 10

−9

sec

Simple Simple Simple

Step No. Iteration KM KM3 Iteration KM KM3 Iteration KM KM3

1 19108 14 14 28696 26 26 26454 35 35

5 3332 24 20 6363 121 88 7960 238 174

10 1559 27 20 8477 101 75 9146 179 135

t, ??? 2880 61 47 7020 233 184 8580 435 347

Finite-Diﬀerence Methods Implemented in SATURN Complex 347

1.4 Parallel Techniques

As mentioned above, the numerical solution to many classes of multidi-

mensional time-dependent problem classes entails high computational costs.

Therefore, parallel algorithms oriented to advanced high-performance multi-

processor computer systems are required. The development of highly eﬃcient

algorithms for parallelization of the problem class under discussion is an in-

volved methodological problem. There are a number of objective reasons for

this, among which the following should be primarily mentioned.

1. As known, implicit schemes are mainly used for the numerical solution to

the transport problems, hence, spatial grid cell computations should be

performed in some strictly determined sequence. When using nonorthog-

onal spatial time-varying grids, the sequence of the cell computation can

be diﬀerent at diﬀerent timesteps. In other words, in parallelization of

this problem class over spatial variables it is very hard, in contrast to the

problem classes using explicit numerical methods, to ensure a simultane-

ous uniform loading of all processing elements used.

2. In numerical solution to nonlinear transport equations the costs of the

transport equation coeﬃcient computation are signiﬁcantly diﬀerent at

diﬀerent spatial points, which leads to an additional disbalance of the

parallel computations.

3. In the numerical solution of the problem class under discussion a number

of other physical processes must be calculated simultaneously with the

simulations of the transport processes in separate subregions, which also

signiﬁcantly inﬂuences the parallel computation balance.

We have developed a ﬁne-grain parallelization method to solve the above

problems on multiprocessor computers in the spatial two-dimensional ap-

proximation. The method is oriented to the case of arbitrary nonorthogonal

spatial grids. It admits spatial problem decomposition to a fairly large num-

ber of processors with arrangement of balanced computations.

Principal concepts of the ﬁne-grain parallelization method

• The principle of spatial decomposition of the initial system to subdomains

(paradomains) for the data allocation over the processors

• The pipeline computation of the paradomain along the particle ﬂight direc-

tions with internal boundary conditions calculated at the current iteration,

which preserves the computation eﬃciency and accuracy

• Loading of temporarily idling processors with proﬁtable computations re-

lating to calculation of additional coeﬃcients, which the solution is ex-

pressed by.

• Using a combined approach with simultaneous parallelization over the sub-

domains and by angular variable µ.

• When solving the multi-group transport problems, the spatial decompo-

sition principle is used in combination with the parallelization by energy

groups.

348 R.M. Shagaliev et al.

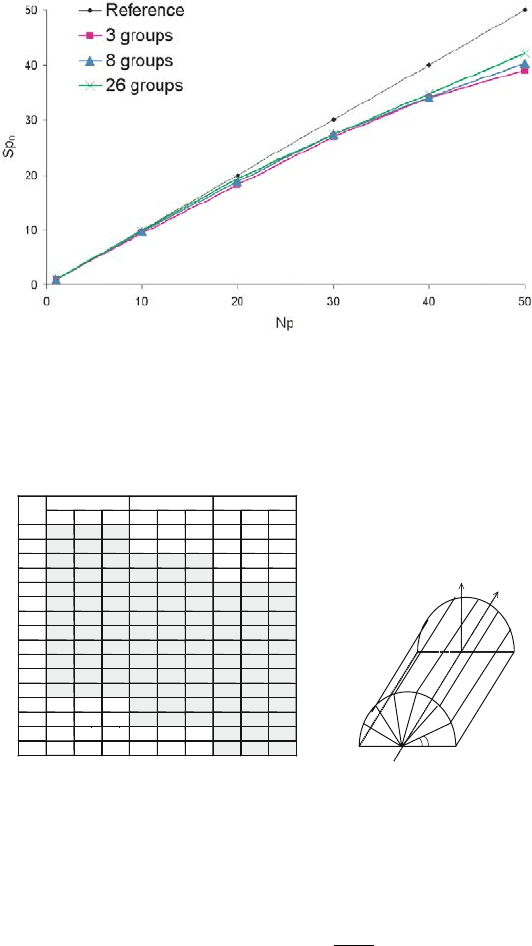
Fig. 16. Acceleration factor versus the number of processors

Time diagram of the solution to the 3D transport equation with

arallelization

Algorithm for pipeline parallelization of 3D

transport equation

Clock Process 1

Process 2 Process 3

µϕΦµϕΦµϕΦ

1 1 1 1------

2 1 1 2------

3 1 2 1 1 1 3-- -

4 1 2 2 1 1 4-- -

5 1 3 1 1 2 3 1 1 5

6 1 3 2 1 2 4 1 1 6

7 2 1 1 1 3 3 1 2 5

8 2 1 2 1 3 4 1 2 6

9 2 2 1 2 1 3 1 3 5

10 2 2 2 2 1 4 1 3 6

11 2 3 1 2 2 3 2 1 5

12 2 3 2 2 2 4 2 1 6

13 - - - 2 3 3 2 2 5

14 - - - 2 3 4 2 2 6

15------2 3 5

16------2 3 6

The 3D particle transport

equation is solved in the

cylindrical coordinate system

Fig. 17. Results of the numerical study of the 3D transport equation parallelization

on a model problem

The results of the numerical studies of the parallelization algorithm eﬃ-

ciency on one model spherical problem are presented below.

Eﬃciency estimation with the magniﬁcation method. The problem size

on each processor remains constant. Sp

∗N

. 900 computational cells

per processor. The results are presented in Fig. 16.

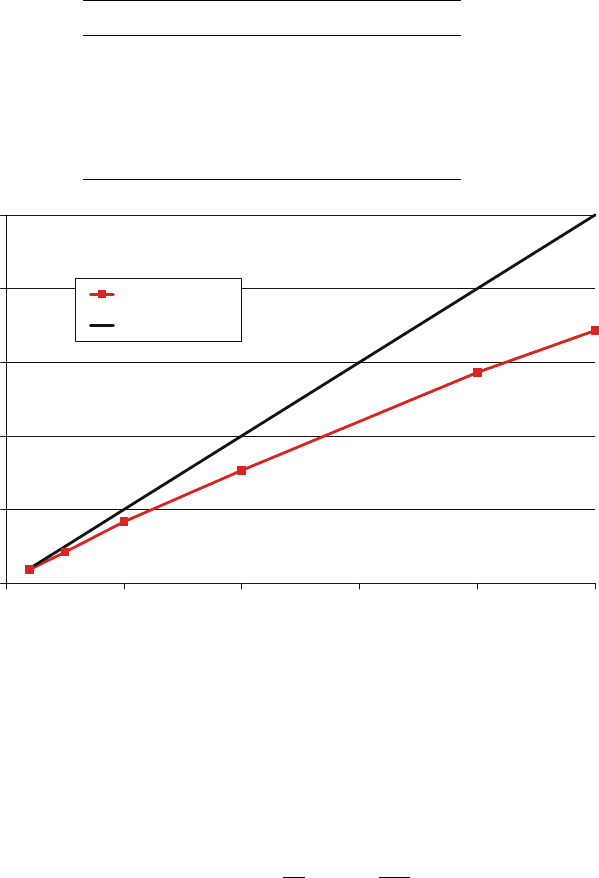
Finite-Diﬀerence Methods Implemented in SATURN Complex 349

Results of the numerical studies of eﬃciency

Nproc Sp

En, %

21.84 92

54.23 85

10 8.33 83

20 15.3 77

40 28.6 71

50 34.3 69

01020304050

Nproc

Computation

Reference

Fig. 18. Acceleration factor versus the number of processors

Algorithm for Pipeline Parallelization of 3D Transport Equation

The pipeline parallelization algorithm has been developed by us and has

been being successfully used for many years in solution to three-dimensional

transport problems (Fig. 17).

The eﬃciency estimation with the reﬁnement method. The total size of

the problem remains constant. Sp

, E

∗ 100%.

Problem parameters: 8 energy groups, 96 particle ﬂight directions (S

250000 3D spatial cells. The results of the numerical studies are summarized

in the next table and in Fig. 17.

350 R.M. Shagaliev et al.

III

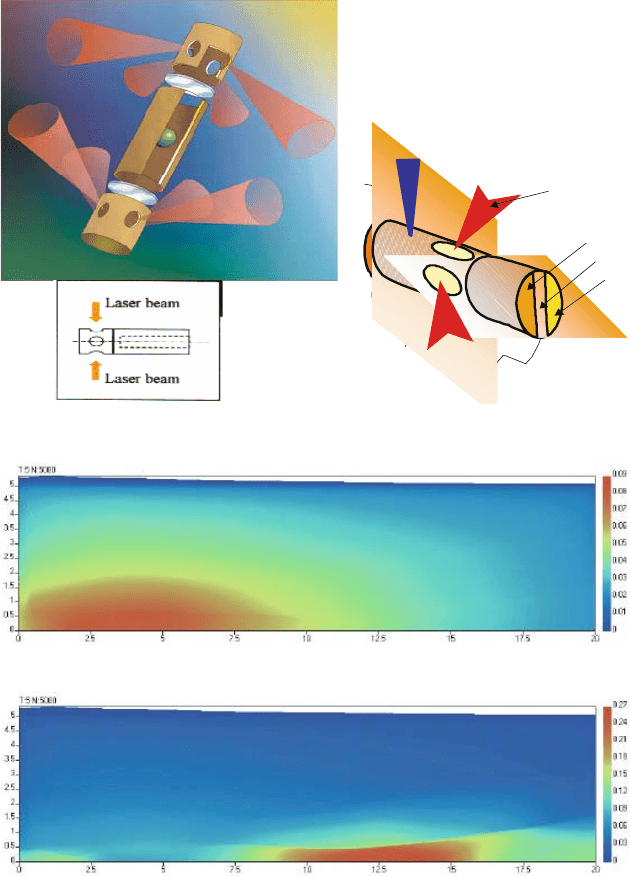
1- holder,

2- laser beams,

3- «ILLUMINATOR»,

4- cylindrical box,

I – III– zones where materials

to be studied are located.

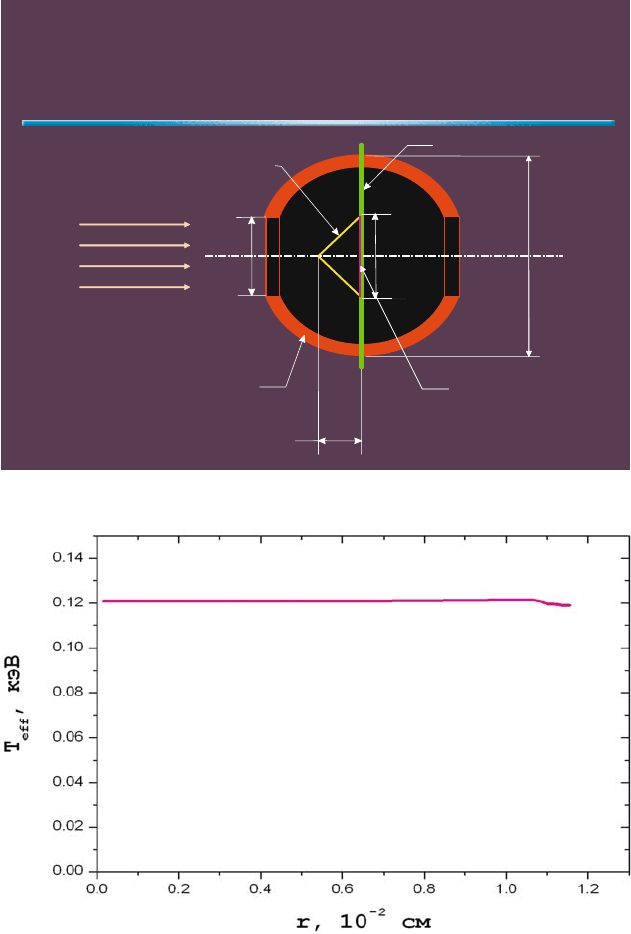
Numerical simulation of experiments on laser facility ISKRA-5

Fig. 19. The “illuminator” target

(a)

(b)

Fig. 20. Distribution of eﬀective temperature of radiation (a) and electrons (b)

inside the cylinder at time 5 ns. Length scale: 100 µm; temperature scale: keV

Finite-Diﬀerence Methods Implemented in SATURN Complex 351

Design of the “labyrinth” target used for X-ray field generation

on the sample surface in the experiments to study the equation of

state with the shock compression method on facility «ISKRA-5»

cone

film

box

disk

laser

radiation flux

Fig. 21. The “labyrinth” target

Fig. 22. Distribution of radiation eﬀective temperature in the outlet cross section.

“Labyrinth” problem

352 R.M. Shagaliev et al.

(a)

(b)

Fig. 23. Distribution of electron temperature (a) and eﬀective temperature of

radiation (b) at the time of peak laser pulse. “Labyrinth” problem

1.5 Some Examples of Computations for 2D Application Problems

The above-discussed numerical methods and algorithms are widely used

presently for computations of diﬀerent application problems in multidimen-

sional geometries.

To demonstrate the capabilities of the methods developed, below are some

results of the computations for 2D coupled time-dependent problems that

describe experiments on laser facility ISKRA-5 (Figs. 19–23).

Implicit Solution of Non-Equilibrium

Radiation Diﬀusion Including Reactive

Heating Source in Material Energy Equation

Dana E. Shumaker

and Carol S. Woodward

Lawrence Livermore National Laboratory

shumaker1@llnl.gov

Lawrence Livermore National Laboratory

cswoodward@llnl.gov

1 Introduction

In this paper, we investigate performance of a fully implicit formulation and

solution method of a diﬀusion-reaction system modeling radiation diﬀusion

with material energy transfer and a fusion fuel source. In certain parameter

regimes this system can lead to a rapid conversion of potential energy into

material energy. Accuracy in time integration is essential for a good solution

since a major fraction of the fuel can be depleted in a very short time. Such

systems arise in a number of application areas including evolution of a star [1]

and inertial conﬁnement fusion [2].

Previous work has addressed implicit solution of radiation diﬀusion prob-

lems [3–8]. More recent work has looked at implicit and semi-implicit so-

lution of reaction-diﬀusion systems. In general, a fully implicit method has

been found to be the most accurate method for diﬃcult coupled nonlinear

equations [9, 10]. In previous work, we have demonstrated that a method of

lines approach coupled with a BDF time integrator and a Newton-Krylov

nonlinear solver could eﬃciently and accurately solve a large-scale, implicit

radiation diﬀusion problem [7, 8]. In this paper, we extend that work to in-

clude an additional heating term in the material energy equation and an

equation to model the evolution of the reactive fuel density. This system now

consists of three coupled equations for radiation energy, material energy, and

fuel density. The radiation energy equation includes diﬀusion and energy ex-

change with material energy. The material energy equation includes reaction

heating and exchange with radiation energy, and the fuel density equation

includes its depletion due to the fuel consumption.

In many applications, the added heat source involves a reaction rate with

a strong nonlinear dependence on material temperature and thus provides a

good test for an implicit solution method. We use an approximation to the

reaction rate valid for temperature regimes less than 1 keV where the rate

has its strongest dependence on material temperature. In particular, the rate

354 D.E. Shumaker and C.S. Woodward

depends on temperature to the ﬁfth power in this regime. While the actual

reaction rate drops oﬀ at high temperature, we use the the ﬁfth power ﬁt for

any temperature in order to investigate the performance of implicit solution

techniques on problems with strong nonlinearities.

The remainder of this paper is organized as follows. The next section

describes the model and presents the equations we are solving. Section 3

describes the implicit solution method we employ, and Sect. 4 presents nu-

merical results illustrating accuracy and eﬃciency of the solution method.

Conclusions are presented in the last section.

2 Mathematical Model

We consider a ﬂux-limited formulation of radiation diﬀusion including a

model for heating due to a fusion source term. The evolution of the fusion

fuel density is determined by an equation which models the depletion of the

fuel as its fusion energy is added to the material energy.

The radiation diﬀusion model is given by [11, 12]

∂E

∂t

= ∇·



3ρκ

∇E



∇E



+ cρκ

) ·



− E



, (1)

where E

(x,t) is the radiation energy density (x =(x, y, z)), T

(x,t)isthe

material temperature, ρ(x) is the material density, c is the speed of light,

and a =4σ/c where σ is the Stephan–Boltzmann constant. The Rosseland

opacity, κ

, is a nonlinear function of the radiation temperature, T

,which

is deﬁned by the relation E

= aT

. The Planck opacity, κ

, is a nonlin-

ear function of material temperature, T

, which is related to the material

energy through an equation of state, E

= EOS(T

). In this paper, when

we use variable opacity and speciﬁc heat their values are taken from the

LEOS equation-of-state package [13] which determines opacities and speciﬁc

heats via table look-up. In some simpliﬁed test problems we use the relation,

= ρc

, for the speciﬁc heat and constant values for opacities. In the

ﬂux limiter, the norm ·is taken to be the l

norm of the gradient vector. In

the simulations presented here we use either Dirichlet or Neumann boundary

conditions on the radiation energy.

This equation is solved in conjunction with two other equations. One

equation expresses the conservation of material energy [11, 12] given by

∂E

∂t

= −cρκ

) ·



− E



+ e





. (2)

The heating term is controlled by a fusion model [14](p. 13) of fuel density

given by

Implicit Solution of Non-Equilibrium Radiation Diﬀusion 355

∂ρ

∂t

= −σ





, (3)

where

is the fuel density. This evolution equation has been used in con-

trolled fusion models [15].

The ﬁt to the reaction rate gives, σ

=1.43 × 10

sec−g

, with a ref-

erence temperature, T

, of 1 keV. For the energy per reaction we use,

=1.35 × 10

erg

sec−g

. This value corresponds to the alpha particle energy

from deuterium tritium fusion. We neglect the neutron energy from the reac-

tion and assume the alpha particle has zero range, thus depositing its energy

locally.

Both the material energy and the fuel density equations contain the non-

linear temperature dependence term (T

)

. This dependency is a good

ﬁt to a tritium-deuterium reaction rate at low temperature (less than a few

keV) such as in a tokamak fusion experiment [16]. The reference temperature,

, is a normalization constant (1 keV) included to simplify the units of the

ﬁtted reaction rate σ

. The actual reaction is less strongly dependent on T

above 1 keV, but, as noted above, we will use this approximation above that

temperature.

The fusion fuel is assumed to be a 50:50 mixture of tritium and deuterium

with

representing the tritium or deuterium density. The binary nature of

the reaction leads to the

dependence in the reaction rate. The energy

per reaction added to the material energy equation is e

Obviously there are a signiﬁcant number of physical processes omitted

from this simple model. One relevant to the deposition of heat, is that we as-

sume the energy of reaction is deposited locally. The correct physical process

would distribute the heat spatially due to the ﬁnite range of the charged

particles in the matter. We chose not to model this nonlocal eﬀect here.

3 Numerical Methods

In this section we present both the spatial and temporal discretization meth-

ods used for solution of the system (1)–(3).

3.1 Spatial Discretization

For spatial discretization, we employ a cell-centered ﬁnite diﬀerence scheme.

We use a tensor product grid with N

, and N

cells in the x, y, and

z directions, respectively. Deﬁning E

R,i,j,k

(t) ≈ E

i,j,k

,t), E

M,i,j,k

(t) ≈

i,j,k

,t), and ρ

F,i,j,k

(t) ≈ ρ

i,j,k

,t) with x

i,j,k

=(x

), and

≡

⎛

⎜

⎝

R,1,1,1

R,N

⎞

⎟

⎠

≡

⎛

⎜

⎝

M,1,1,1

M,N

⎞

⎟

⎠

≡

⎛

⎜

⎝

F,1,1,1

F,N

⎞

⎟

⎠