Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


44 Fundamentals
1.5 a. Find the stream function for the two-dimensional incompressible flow with
velocity components v = x
2
−2xy cos y
2
−2xy +sin y
2
0.
b. Find the discharge per unit between the points 1and (0, 0).
1.6 For the following flows, find the missing velocity component needed for the
flow to satisfy the incompressible continuity equation.
a. v
x
=x
2
+y
2
+a
2
v
y
=−xy −yz −xz v
z
=?
b. v
x
=ln
y
2
+z
2
v
y
=sin
x
2
+z
2
v
z
=?
c. v
x
=?v
y
=
y
x
2
+y
2
+z
2
3/2
v
z
=
z
x
2
+y
2
+z
2
3/2
.
1.7 For the flow field given by =A lnx
2
+y
2
+yS, find the discharge per unit
width in the z direction between the points (1, 1, 0) and −1 −1 0.
1.8 Find the stream function for the two-dimensional incompressible flow with
a radial velocity (cylindrical polar coordinates) given by v
r
=
A
√
r
cos. Also find the
missing velocity component.
1.9 Find the stream function for the two-dimensional incompressible flow with
velocity components given by v
r
=U
1−
a
2
r
2
cos v
=−U
1+
a
2
r
2
sin .
1.10 Find the stream function for the two-dimensional incompressible flow
with radial velocity component v
r
=
3
2
Ar
3/2
cos
3
2
. Also find the missing velocity
component.
1.11 Find the stream function for the velocity field v =
x
2
−2x +1
−2xy +2y −x 0
.
1.12 For steady, incompressible inviscid flows with body forces neglected, it was
shown by Yih (1958) that the flow can be reduced to that of a constant-density flow by
the transformation
v
∗
x
=
0
v
x
v
∗
y
=
0
v
y
v
∗
z
=
0
v
z
where
0
is a constant reference density. Verify this result.
1.13 Find the rates of deformation and vorticity in Cartesian coordinates for the
velocity field
v =
Bx
x
2
+y
2
+z
2
3/2
By
x
2
+y
2
+z
2
3/2
Bz
x
2
+y
2
+z
2
3/2
1.14 a. Compute the unit normal for the inclined surface shown.
b. For the stress vector with components
b
=
10 3 7
, calculate the normal
and tangential components of the stress vector on the inclined surface.
1.15 Given the velocity field v = 5yi, find the circulation about a rectangle 6 units
long and 4 units high, centered at the origin. Compute it two ways, once by the line
integral and again using the area formula.
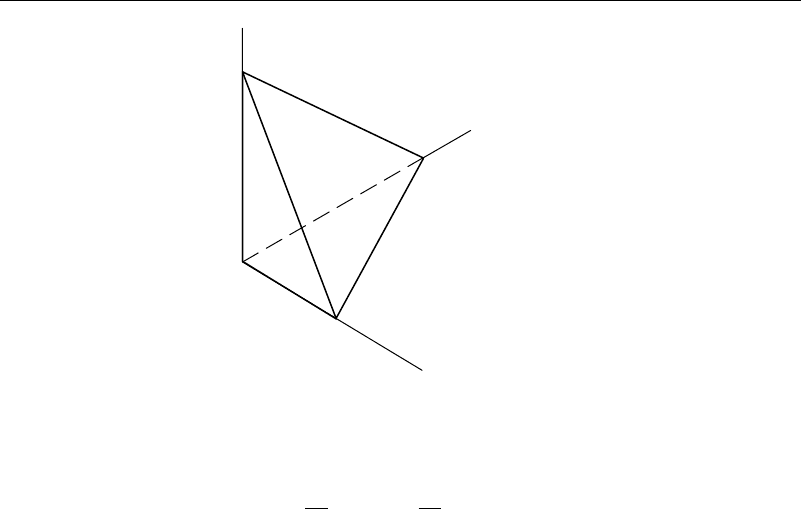
Problems—Chapter 1 45
5
y
4
3
x
z
Figure P1.14 Problem1.14—Stress tetrahedron
1.16 For two dimensional incompressible flow, insert the stream function
v
x
=
y
v
y
=−
x
into the Navier-Stokes equation, and eliminate the pressure to find the governing equa-
tion for the stream function.

Chapter 2
Inviscid Irrotational Flows
2.1 Inviscid Flows 46
2.2 Irrotational Flows and the
Velocity Potential 47
2.2.1 Intersection of Velocity
Potential Lines and Stream-
lines in Two Dimensions 49
2.2.2 Basic Two-Dimensional
Irrotational Flows 51
2.2.3 Hele-Shaw Flows 57
2.2.4 Basic Three-Dimensional
Irrotational Flows 58
2.2.5 Superposition and the
Method of Images 59
2.2.6 Vortices Near Walls 61
2.2.7 Rankine Half-Body 65
2.2.8 Rankine Oval 67
2.2.9 Circular Cylinder or Sphere
in a Uniform Stream 68
2.3 Singularity Distribution Methods 69
2.3.1 Two- and Three-Dimensional
Slender Body Theory 69
2.3.2 Panel Methods 71
2.4 Forces Acting on a
Translating Sphere 77
2.5 Added Mass and the Lagally
Theorem 79
2.6 Theorems for Irrotational Flow 81
2.6.1 Mean Value and Maximum
Modulus Theorems 81
2.6.2 Maximum-Minimum
Potential Theorem 81
2.6.3 Maximum-Minimum
Speed Theorem 82
2.6.4 Kelvin’s Minimum Kinetic
Energy Theorem 82
2.6.5 Maximum Kinetic Energy
Theorem 83
2.6.6 Uniqueness Theorem 84
2.6.7 Kelvin’s Persistence of
Circulation Theorem 84
2.6.8 Weiss and Butler Sphere
Theorems 84
Problems—Chapter 2 85
2.1 Inviscid Flows
Finding solutions with the Navier-Stokes equations that were introduced in Chapter 1 is
a formidable challenge, particularly for flows where convective acceleration is present.
When, however, the Reynolds number is sufficiently high, of the order of 10
5
or more,
viscosity effects usually are of importance to the flow only in the boundary layer near a
body or a wall or possibly in confined regions in the wake of a body. In many problems,
such as the case of waves on a free surface, viscosity effects many be of secondary
importance in most of the flow field.
46

2.2 Irrotational Flows and the Velocity Potential 47
In solving such flows, it is convenient—and useful—to first omit viscosity terms
completely. Since this reduces the order of the differential equations, this means that
fewer boundary conditions can be applied. The zero normal velocity condition generally
is the most important condition and so is retained, whereas the no-slip velocity condition
is ignored. For many flows, viscous effects can be included later by considering the
boundary layer flow using the slip velocity found from the inviscid flow at the outer
edge of the boundary layer.
Most 19th-century fluid mechanics was concerned with the study of inviscid flows.
1
There was no clear understanding of the effects of the Reynolds number on the flow, and
the study of turbulence was left largely untouched. This was, however, a time of great
ferment in the fields of fluid mechanics, electricity and magnetism, and thermodynamics.
Particularly in the first two areas, scientists discovered a great similarity in their fields,
and it was not unusual for a researcher to make contributions in both. As a result, today
both fields share many terms such as source, sink, potential, and current, among others.
Workers in one field often use analogies in the other, perhaps feeling that the other field
can give a clearer understanding. In this chapter, the electrical and magnetic analogies
are set aside, but keep in mind that despite this, a minor change in terminology is all
that is needed to change the topic to electrostatics, electrodynamics, and magnetostatics.
If viscosity terms are omitted in the Navier-Stokes equations, they reduce to the form
Dv
Dt
=−p +g (2.1.1)
This is called the Euler equation.
2.2 Irrotational Flows and the Velocity Potential
From the circulation theorem (equation 1.12.2b), if mass density is constant and viscous
effects can be neglected, D/Dt =
C
−
1
p
·ds. The integrand on the right-hand
side of the equation is an exact differential, so the integral around the path vanishes.
Consequently, for a flow with no upstream circulation, as the flow moves downstream,
it must continue to be vorticity-free, or irrotational. This is called the persistence of
irrotationality. (In a real fluid, viscosity effects will introduce vorticity at a boundary,
but at high Reynolds numbers this vorticity will be convected downstream and chiefly
confined to the vicinity of the boundary and the wake.)
By the definition of irrotational flows,
= ×v = 0 (2.2.1)
This suggests that two of the velocity components can be solved for in terms of the
third component or, alternatively, that, as in the case of the continuity equation, scalar
functions can be introduced that have the effect of accomplishing this.
An easier approach is to realize that since for irrotational flows =
C
v ·ds = 0
for any C, it follows that the integrand v·ds must be an exact differential, and therefore
for an irrotational flow field with velocity v, it must be expressible as the gradient of a
scalar. This allows us to write
v = (2.2.2)
1
Inviscid fluids do not exist, but fluids can flow in such a manner that viscosity effects are negligible in
most of the region of flow.

48 Inviscid Irrotational Flows
where is called the velocity potential. For any velocity field written as the gradient
of a scalar as in equation (2.2.2), it is guaranteed that for any scalar function , v will
automatically be an irrotational velocity field. Because of equation (2.2.2), irrotational
flows are often also called potential flows.
From equation (2.2.2) it follows that surfaces of constant are locally orthogonal to
the velocity vector. Thus, surfaces of constant must be orthogonal to stream surfaces.
The introduction of a velocity potential guarantees irrotationality, but it is still
required that the flow field satisfy the basic dynamical equations. To simplify the
discussion, we will consider only incompressible flows. Then continuity requires that
the divergence of the velocity field vanish. Therefore, the continuity equation for an
irrotational incompressible flow is
0 = ·v =
2
(2.2.3)
This equation, called the Laplace equation, is used to determine for a given flow
situation.
What then of the dynamics of the flow? Our flow field at this point seems to
be completely determined from irrotationality and continuity, yet we have not con-
sidered Euler’s equation. From equations (1.2.3) and (2.1.1), since ×v = 0, Euler’s
equation (2.1.1) can be written in the form
v
t
+
v
2
2
=−p +g
For irrotational flows v = , and g can be written as g =−gh, where h is the
elevation of the point in the direction in which gravity acts. Euler’s equation can then be
rearranged and, after dividing by , becomes the form
t
+
1
2
v
2
+gh +
p
=0.
Upon integration this gives
t
+
1
2
v
2
+gh +
p
=ft (2.2.4)
where ft is a constant or at most a function of time and is determined from either
conditions at a reference point or a point far upstream. Equation (2.2.4) is known as the
Bernoulli equation for irrotational flows.
The Bernoulli equation could also have been derived for the case where mass density
depends only on pressure. In that case, the p/ term in equation (2.2.4) would be replaced
by
dp/.
For most incompressible flows, then, the velocity field is found using only the
conditions of irrotationality (usually by the introduction of the velocity potential )
and the continuity equation in the form of equation (2.2.3), along with the imposition
of conditions on the normal velocity at boundaries. Once is known, pressure can be
found from the Bernoulli equation (2.2.4). Note that all of the mathematical nonlin-
earities appear only in the Bernoulli equation. For interface problems, however, further
nonlinearities can be introduced by boundary conditions.
The linearity of equation (2.2.3) allows for the superposition of velocity fields. The
nonlinearity of equation (2.2.4) means that pressure fields cannot be superposed in a
linear manner.

2.2 Irrotational Flows and the Velocity Potential 49
Note that for irrotational flows equation (2.2.1) can be written as
=
C
·ds =
2
−
1
= (2.2.5)
where
1
and
2
are the values of the velocity potential at the start and end points of
the traverse of C. Thus, if is a single-valued function (i.e., if we go around a closed
loop and the value of has not changed), since the curve C is closed, will be zero.
It is, however, possible that can be multivalued if there exist points or isolated
regions where is either singular or not uniquely defined. A line vortex, described
following, has one such nonuniquely defined potential function. For such functions
the circulation will usually be different from zero. Multivalued velocity potentials are
associated with the presence of vorticity, corresponding to multivalued stream functions
that are associated with discharge.
Since we will be looking at some methods for solving Laplace’s equation, you may
wonder whether any solution you might have obtained for a given flow is unique. That
is, if you and your neighbor both solve the same problem but use different methods,
will you end up with the same velocity field? The answer is yes, provided that you
both stay with the same set of rules (and, of course, both do your work accurately). The
irrotational flow field around a body is unique for a given set of boundary conditions,
provided we also specify the circulation and do not allow the development of cavities
that do not contain fluid. Always remember that the primary interest is in finding a
flow field that models a real physical phenomenon to some degree of accuracy. Since
vorticity, and hence circulation, is present in the boundary layer, it may need to be
included in a model to give a realistic model of the flow field. Cavities might possibly
be a reasonable model for wake flows. As long as the circulation is prescribed, together
with rules concerning whether or not cavities are present, the flow field will be unique.
It is possible that the methods used to solve Laplace’s equation will introduce a
“mathematical” flow inside a body as well. In that region the flow is not unique. Any
flows that methods generate inside bodies lie outside our domain of interest and are
artifices of the mathematics with little if any physical meaning.
2.2.1 Intersection of Velocity Potential Lines and Streamlines
in Two Dimensions
Surfaces of constant velocity potential and of constant stream function intersect one
another throughout the flow. Since by definition the velocity is always normal to a
constant potential surface, it follows that the constant stream surfaces are generally
perpendicular to the constant potential surfaces. There are some exceptions to this, such
as near stagnation points. We next investigate this for two-dimensional flows to see at
what angles these intersections can take place.
To see the relationship between and lines, start with
d =
x
dx +
y
dy =v
x
dx +v
y
dy
and
d =
x
dx +
y
dy =−v
y
dx +v
x
dy

50 Inviscid Irrotational Flows
From these it follows that the slope of a = constant line d = 0 is given by
dy
dx
=−
v
x
v
y
and the slope of a = constant line d = 0 is given by
dy
dx
=+
v
y
v
x
Multiplying the two slopes gives
dy
dx
dy
dx
=−1
which leads to the conclusion that constant and lines are orthogonal to one another
except possibly at places where the velocity is either zero (stagnation points) or infinite
(singularities).
In either of these two special cases we can investigate the situation further by
considering the second-order terms to see what occurs. For example, at a stagnation
point a Taylor series expansion gives to second-order terms in dx and dy
d =
x
dx +
y
dy +
2
x
2
dx
2
2
+
2
xy
dxdy +
2
y
2
dy
2
2
Since the first derivatives vanish at the stagnation point, on a line of constant passing
through a stagnation point this expression becomes
d =
2
x
2
dx
2
2
+
2
xy
dxdy +
2
y
2
dy
2
2
First-order terms vanish at the stagnation point, so this becomes
0 =
2
x
2
+2
2
xy
dy
dx
+
2
y
2
dy
dx
2
dx
2
2
Solving this quadratic equation for the slope at the stagnation point, we have
dy
dx
=
−
2
xy
±
2
xy
2
−
2
x
2
2
y
2
2
y
2
A similar expression can be found involving by the same process.
Note that the term underneath the square root sign must always be positive, since
by Laplace’s equation
2
x
2
=−
2
y
2
and so this term is the sum of two squares.
The conclusion then is that there will be two values for the slope at the stagnation
point, hence the line divides, or bifurcates, at that point. For details of the angle between
and , individual examples must be considered. Since the Laplace equation is a great
averager of things (for instance, it can be shown from the Gauss-Green theorems that the
value of at the center of a circle is the average of all the values it takes on the circle), the
constant lines can be expected to fall midway between the constant lines.

2.2 Irrotational Flows and the Velocity Potential 51
2.2.2 Basic Two-Dimensional Irrotational Flows
Next, consider several basic simple flows that are the building blocks of potential flow
theory from which all other potential flows can be constructed. These basic flows have
their counterparts in electrostatics and electromagnetics (point charges, dipoles), beam
deflection theory (concentrated loads), and many other branches of engineering physics,
and they are special cases of what are termed Green’s functions.
In two-dimensional flows the basic solutions must satisfy the equations
v
x
=
x
=
y
(2.2.6a)
and
v
y
=
y
=−
x
(2.2.6b)
Also, the equation
2
=0 (2.2.7)
is the incompressible continuity equation for irrotational flows, corresponding to
·v = 0, while
2
= 0 (2.2.8)
is the irrotationality condition for two-dimensional incompressible flows satisfying con-
tinuity, corresponding to
z
=0. These must be satisfied as well.
Uniform stream
A uniform stream is a flow whose velocity is the same at every point in space. Therefore,
the velocity components are
v
x
=U
x
=
x
(2.2.9a)
and
v
y
=U
y
=
y
(2.2.9b)
Integrating equations (2.2.9a) and (2.2.9b), we find that
uniform stream
=xU
x
+yU
y
(2.2.10)
where the constant of integration has arbitrarily been set to zero, since it does not
contribute to the velocity field in any way. Lines of constant and (both are straight
lines and mutually orthogonal) are shown in Figure 2.2.1. The stream function is found
from use of equations (2.2.6a) and (2.2.6b) to be
uniform stream
=yU
x
−xU
y
(2.2.11)

52 Inviscid Irrotational Flows
Streamlines Potential Lines
θ
U
Figure 2.2.1 Uniform stream streamlines and iso-potential lines
Line source or sink (monopole)
The velocity potential
=
m
2
ln
r −r
0
=
m
2
ln
x −x
0
2
+y −y
0
2
(2.2.12)
is called a line source (if m is positive) or line sink (if m is negative) of strength m,
located at the point x
0
y
0
. It extends from − to + in the z direction. The velocity
components are given by
v
x
=
x
=
mx −x
0
2
r −r
0
2
(2.2.13a)
and
v
y
=
y
=
my −y
0
2
r −r
0
2
(2.2.13b)
Differentiating the velocity components gives
2
x
2
=
m
2
r −r
0
4
r −r
0
2
−2x −x
0
2
and
2
y
2
=
m
2
r −r
0
4
r −r
0
2
−2y −y
0
2
=−
2
x
2
Therefore, continuity is satisfied everywhere except possibly at the point x
0
y
0
.
To investigate what is happening at the location of the source itself, integrate the
flow normal velocity abouta1by1square centered at x
0
y
0
, as is seen in Figure 2.2.2.
(The size and shape of the square is actually arbitrary, since the same result would be

2.2 Irrotational Flows and the Velocity Potential 53
x
y
(1, –1, 0)(–1, –1, 0)
(–1, 1, 0) (1, 1, 0)
Figure 2.2.2 Source/sink discharge calculation
obtained for a contour of any size or shape that encloses the source.) Starting from the
definition of discharge, we have
Q =
y
0
+1
y
0
−1
v
x
1y−v
x
−1 ydy +
x
0
+1
x
0
−1
v
y
x 1 −v
y
x −1dx
=
y
0
+1
y
0
−1
m
2
1
1+y −y
0
2
−
−1
1+y −y
0
2
dy
+
x
0
+1
x
0
−1
m
2
1
1+x −x
0
2
−
−1
1+x −x
0
2
dx = m
Thus, m represents the flow rate per unit length in the z direction being emitted from
the source at x
0
y
0
, and is called the strength of the source. Lines of constant
(concentric circles) and (radial lines) are shown in Figure 2.2.3.
The issue of rotationality at x
0
y
0
should also be considered. If the circulation
around a square similar to the one we just used is computed, the result is zero. There-
fore, there is a concentrated source of mass at x
0
y
0
but no concentrated source of
vorticity there.
From equations (2.2.6a) and (2.2.6b) the stream function for a source is seen to be
=
m
2
tan
−1
y −y
0
x −x
0
(2.2.14)
The arctangent is a multivalued function, changing by 2 as we go around a contour
enclosing from equations (2.2.6a) and (2.2.6b). Therefore, the change in as we go
around the contour is m, consistent with its representation of rate of flow.
From equation (2.2.12) we see that constant lines are concentric circles centered
at x
0
y
0
. From equation (2.2.14), we see that the constant lines are radial lines
emanating from x
0
y
0
. Thus, the flow will be along the radial streamlines emanating
from x
0
y
0
. To conserve mass, the velocity must decrease inversely with the distance
from x
0
y
0
.
