Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


14 Fundamentals
infinitesimal element its value is thus −pn dS—the minus sign because the pressure
force acts toward the area dS and thus is opposite to the unit normal.
The viscous force in general will have both normal and tangential components. For
now, simply write it as
n
dS acting on a small portion of the surface, where
n
is
called the stress vector. It is the force per unit area acting on the surface dS. The n
superscript reminds us that the stress vector is applied to a surface with normal pointing
in the n direction.
The gravity force per unit volume is written as g dV , where the magnitude of g is 9.80
or 32.17, depending on whether the units used are SI or British. The net force is then
S
−pn +
n
dS +
V
g dV
Equating this to the net change in momentum gives
V
Dv
Dt
dV =
S
−pn +
n
dS +
V
g dV (1.5.2)
Use of the divergence theorem allows us to write
S
−pn dS =
V
−p dV (1.5.3)
This reduces equation (1.5.2) to
V
Dv
Dt
dV =
V
−p +gdV +
S
n
dS (1.5.4)
At this point a similar simplification for the viscous term is not possible. This term is
investigated further in the next section.
1.6 Stress
Stress is defined as a force applied to an area divided by that area. Thus, two directions
are associated with stress: the direction of the force and the direction (orientation) of the
area. Therefore, stress has a more complicated mathematical structure than does either
a scalar or a vector. To put this into its simplest form, three special stress vectors will
be introduced that act on mutually orthogonal surfaces whose faces are orientated with
normals along our coordinate axes.
When a material is treated as a continuum, a force must be applied as a quantity
distributed over an area. (In analysis, a concentrated force or load can sometimes be a
convenient idealization. In a real material, any concentrated force would provide very
large changes—in fact, infinite changes—both in deformation and in the material.) The
previously introduced stress vector
n
, for example, is defined as
n
= lim
S→0
F
S
(1.6.1)
where S is the magnitude of the infinitesimal area. In the limit as S approaches zero
the direction of the normal to S is held fixed.
It appears that at a given point in the fluid there can be an infinity of different
stress vectors, corresponding to the infinitely many orientations of n that are possible.
To bring order out of such confusion, we consider three very special orientations of n
and then show that all other orientations of n produce stress vectors that are simply
related to the first three.

1.6 Stress 15
τ
(–y
)
τ
(–z
)
n
(–x
)
n
(–y
)
τ
(–x
)
n
(–z
)
n
x
y
τ
z
Figure 1.6.1 Stress vector
First consider the three special stress vectors
x
y
z
, corresponding to forces
acting on areas with unit normals pointing in the x, y, and z directions, respectively.
These act on the small tetrahedron shown in Figure 1.6.1. For a force F acting on a
surface S
x
with unit normal pointing in the x direction (thus, n = i), write the stress
on this face of our tetrahedron as
x
= lim
A
x
→0
F
A
x
=
xx
i +
xy
j +
xz
k (1.6.2)
where
xx
is the limit of the x component of the force acting on this face,
xy
is the
limit of the y component of the force acting on this face, and
xz
is the limit of the z
component of the force acting on this face.
Similarly, for normals pointing in the yn = j and zn = k directions we have
y
= lim
A
y
→0
F
A
y
=
yx
i+
yy
j+
yz
k (1.6.3)
and
z
= lim
A
z
→0
F
A
z
=
zx
i+
zy
j+
zz
k (1.6.4)
As in equation (1.6.2), the first subscript on the components tells the direction that
the area faces, and the second subscript gives the direction of the force component on
that face.
Upon examination of the three stress vectors shown in equations (1.6.2), (1.6.3),
and (1.6.4), we see that they can be summarized in the matrix form
=
⎛
⎝
x
y
z
⎞
⎠
=
⎛
⎝
xx
xy
xz
yx
yy
yz
zx
zy
zz
⎞
⎠
⎛
⎝
i
j
k
⎞
⎠
The nine quantities in this 3 by 3 matrix are the components of the second-order stress
tensor.
In the limit, as the areas are taken smaller and smaller, the forces acting on the four
faces of the tetrahedron are −
x
dS
x
−
y
dS
y
−
z
dS
z
, and
n
dS. The first three
of these forces act on faces whose normals are in the −x −y −z directions. In writing
them we have used Newton’s third law, which tells us that
−x
=−
x
−y
=−
y
,

16 Fundamentals
and
−z
=−
z
. The fourth of these forces acts on the slant face with area dS and
normal n.
Summing the surface forces and using dS
x
= n
x
dS dS
y
= n
y
dS dS
z
= n
z
dS,
the result is
F
S
=−
x
dS
x
−
y
dS
y
−
z
dS
z
+
n
dS
=−
x
n
x
−
y
n
y
−
z
n
z
+
n
dS
(1.6.5)
Considering the summation of forces as the tetrahedron shrinks to zero, we have
F
S
+F
V
=
Dv
Dt
dV
Our surface forces depend on dS, and thus are second order in the tetrahedron dimen-
sions. The body forces and the mass times acceleration terms depend on dV, which is
of the third order in the tetrahedron dimensions. If in our analysis the tetrahedron is
decreased in size, the dV terms approach zero faster than do the dS terms. Thus, the
body force and acceleration terms are of higher (third) order in the dimensions of the
tetrahedron than the surface force terms (second). In the limit as the tetrahedron goes
to zero, we are thus left with only the second-order terms, resulting in
n
=
x
n
x
+
y
n
y
+
z
n
z
(1.6.6)
Therefore, from knowledge of the three special stress vectors
x
y
z
, we can
find the stress vector in the direction of any n at the same point.
Next, combine equations (1.6.2), (1.6.3), and (1.6.4) with (1.6.6). This gives
n
=n
x
xx
i +
xy
j+
xz
k +n
y
(
yx
i +
yy
j+
yz
k
+n
z
(
zx
i +
zy
j+
zz
k
=in
x
xx
+n
y
yx
+n
z
zx
+jn
x
xy
+n
y
yy
+ n
z
zy
)
+kn
x
xz
+n
y
yz
+n
z
zz
(1.6.7)
the expression after the second equals sign being a rearrangement of the preceding.
Taking the dot product of the three unit vectors i, j, k with (1.6.7) gives
xx
=i ·
x
xy
=j·
x
xz
=k ·
x
yx
=i ·
y
yy
=j·
y
yz
=k ·
y
zx
=i ·
z
zy
=j·
z
zz
=k ·
z
(1.6.8)
This is in agreement with our definition of
xx
(and so on) being the components of the
various stress vectors.
Stress components associated with force components that act in the same direc-
tion as their normal (i.e.,
xx
yy
zz
) are referred to as normal stresses. Stress
components associated with force components that act perpendicular to their normal
(i.e.,
yx
yz
zx
xy
zx
xz
) are referred to as shear stresses. Note that the first
subscript on the components tells us the direction in which the area faces, and the
second subscript gives us the direction of the force component on that face. Positive
sign conventions for viscous stress components are given in Figure 1.6.2. The nine com-
ponents
xx
xy
xz
yx
yy
yz
zx
zy
zzj
of our three special stress vectors
x
y
z
can be shown to be components of a second-order tensor called the

1.6 Stress 17
z
x
τ
yx
τ
yy
τ
yz
τ
xx
τ
xz
τ
xy
τ
zy
τ
zx
τ
zz
τ
zx
τ
zz
τ
zy
τ
yz
τ
yx
τ
yy
τ
xz
τ
xy
τ
xx
y
Figure 1.6.2 Stress tensor sign convention
stress tensor. The stress vectors
x
y
, and
z
are thus expressible in terms of these
nine components, as shown above. As seen from the manner in which the components
of the three stress vectors were introduced while carrying out the development, the
nine-component stress tensor is the collection of the three x, y, z components of each of
these three stress vectors. Thus, the stress tensor is the collection of nine components
of the three special stress vectors
x
y
z
.
Besides its use in formulating the basic equations of fluid dynamics, the stress
vector is also used to apply conditions at the boundary of the fluid, as will be seen
when we consider boundary conditions. The stress tensor is used to describe the state
of stress in the interior of the fluid.
Return now to equation (1.5.4), and change the surface integral to a volume integral.
From equation (1.6.7) we have
s
n
dS =
S
n
x
xx
i +
xy
j+
xz
k +n
y
(
yx
i +
yy
j +
yz
k +n
z
(
zx
i +
zy
j +
zz
kdS
=
V
x
xx
i +
xy
j +
xz
k
+
y
yx
i +
yy
j +
yz
k
+
z
(
zx
i +
zy
j +
zz
k
dV (1.6.9)

18 Fundamentals
=
V
i
xx
x
+
yx
y
+
zx
z
+j
xy
x
+
yy
y
+
zy
z
+ k
xz
x
+
yz
y
+
zz
z
dV
Inserting this into equation (1.5.4) gives
V
Dv
Dt
dV =
V
−p +gdV +
V
i
xx
x
+
yx
y
+
zx
z
+ j
xy
x
+
yy
y
+
zy
z
+k
xz
x
+
yz
y
+
zz
z
dV
(1.6.10)
As was the case for the continuity equation, equation (1.6.10) must be valid no matter
what volume we choose. Therefore, it must be that
Dv
Dt
=−p +g +i
xx
x
+
yx
y
+
zx
z
+j
xy
x
+
yy
y
+
zy
z
+k
xz
x
+
yz
y
+
zz
z
(1.6.11)
Before leaving these equations, note that the continuity equation (1.3.5) and the
momentum equation (1.6.11) can be written in a combined matrix form as
t
⎛
⎜
⎜
⎝
v
x
v
y
v
z
⎞
⎟
⎟
⎠
+
x
⎛
⎜
⎜
⎝
v
x
p −
x
−
xx
−
xy
−
xz
⎞
⎟
⎟
⎠
+
y
⎛
⎜
⎜
⎝
v
y
−
yx
p −
y
−
yy
−
yz
⎞
⎟
⎟
⎠
+
z
⎛
⎜
⎜
⎝
v
z
−
zx
−
zy
p −
z
−
zx
⎞
⎟
⎟
⎠
=0
(1.6.12)
This form of the equations is referred to as the conservative form and is frequently used
in computational fluid dynamics.
Moments can be balanced in the same manner as forces. Using a finite control
mass and taking R as a position vector drawn from the point about which moments are
being taken to a general fluid particle, equating moments to the time rate of change of
moment of momentum gives
d
dt
V
R ×v dV +
S
R ×vv ·n dS
=
S
R ×−pndS +
V
R ×g dV +
S
R ×
n
dS
(1.6.13)
But
d
dt
V
R ×vdV =
V
D
Dt
R ×v +
DR ×v
Dt
dV (1.6.14)

1.6 Stress 19
and using the product rule and the fact that a vector crossed with itself is zero,
DR ×v
Dt
=
DR
Dt
×v +R ×
Dv
Dt
=v ×v +R ×
Dv
Dt
=R ×
Dv
Dt
(1.6.15)
Also, using equation (1.6.7), R ×
n
can be written as
R ×
n
=R ×in
x
xx
+n
y
yx
+n
z
zx
+jn
x
xy
+n
y
yy
+n
z
zy
+kn
x
xz
+n
y
yz
+n
z
zz
=n
x
iy
xz
−z
xy
+jz
xx
−x
xz
+kx
xy
−y
xx
+n
y
iy
yz
−z
yy
+jz
yx
−x
yz
+kx
yy
−y
yx
+n
z
iy
zz
−z
zy
+jz
zx
−x
zz
+kx
zy
−y
zx
(1.6.16)
The surface integral involving
n
then becomes
S
R ×
n
dS =
S
n
x
iy
xz
−z
xy
+jz
xx
−x
xz
+kx
xy
−y
xx
+ n
y
iy
yz
−z
yy
+jz
yx
−x
yz
+kx
yy
−y
yx
+ n
z
iy
zz
−z
zy
+jz
zx
−x
zz
+kx
zy
−y
zx
dS
=
V
x
iy
xz
−z
xy
+jz
xx
−x
xz
+kx
xy
−y
xx
+
y
iy
yz
−z
yy
+jz
yx
−x
yz
+kx
yy
−y
yx
+
z
iy
zz
−z
zy
+jz
zx
−x
zz
+kx
zy
−y
zx
dV (1.6.17)
=
V
i
yz
−
zy
+j
zx
−
xz
+k
xy
−
yx
+ i
y
xz
x
+
yz
y
+
zz
z
−z
xy
x
+
yy
y
+
zy
z
+ j
z
xx
x
+
yx
y
+
zx
z
−x
xz
x
+
yz
y
+
zz
z
+k
x
xy
x
+
yy
y
+
zy
z
−y
xx
x
+
yx
y
+
zx
z
dV
=
V
i
yz
−
zy
+j
zx
−
xz
+k
xy
−
yx
+R ×
i
xx
x
+
yx
y
+
zx
z
+j
xy
x
+
yy
y
+
zy
z
+k
xz
x
+
yz
y
+
zz
z
dV

20 Fundamentals
Thus, using equations (1.6.14), (1.6.15), (1.6.16), (1.6.17), equation (1.6.13) becomes
V
t
R ×v +R×
Dv
Dt
dV +
V
·vR ×vdV =
V
R ×−pdV
+
V
R×g dV +
V
i
yz
−
zy
+j
zx
−
xz
+k
xy
−
yx
+R ×
i
xx
x
+
yx
y
+
zx
z
+ j
xy
x
+
yy
y
+
zy
z
+k
xz
x
+
yz
y
+
zz
z
dV
Collecting terms and rearranging, the result is
V
R ×v
t
+ ·
v
dV +
V
R ×
Dv
Dt
dV
=
V
R ×
−p + g+i
xx
x
+
yx
y
+
zx
z
(1.6.18)
+ j
xy
x
+
yy
y
+
zy
z
+k
xz
x
+
yz
y
+
zz
z
dV
+
V
i
y
z −
zy
+j
zx
−
xz
+k
xy
−
yx
dV
Examining the various terms, it is seen that the integrand in the first integral is
zero by virtue of the continuity equation. The integrand in the last integral on the left
side of the equals sign is R crossed with the mass density times the acceleration, which
is the left side of equation (1.6.11). The integrand in the first integral on the right of
the integral sign is R crossed with the right side of equation (1.6.11). Thus, the two
integrals cancel and we are left with
0 =
V
i
yz
−
zy
+j
zx
−
xz
+k
xy
−
yx
dV
Again, for this to be true for any volume it is the integrand that must vanish. This yields
0 = i
yz
−
zy
+j
zx
−
xz
+k
xy
−
yx
or
yz
=
zy
zx
=
xz
xy
=
yx
(1.6.19)
Thus, equation (1.6.19), the result of summing moments, tells us that the order of writing
the subscripts is immaterial, since the stress due to the y force component acting on the
face with normal in the x direction is equal to the stress due to the x force component
acting on the face with normal in the y direction, and so on for the other two faces. This
interchangeability of the indices tells us that the stress tensor is a symmetric tensor,
and there are only six rather than nine numerically unique values for its components
at a point. (It has been proposed that there is the possibility of a magnetic material
to have an antisymmetric stress tensor. Such a material would indeed have a complex
mathematical description.)

1.7 Rates of Deformation 21
1.7 Rates of Deformation
In the equations developed so far, we have not identified the nature of the material we
are studying. In fact, our equations are so general at this stage that they apply to solid
materials as well as to fluids. To narrow the subject to fluids, it is necessary to show
how the fluid behaves under applied stresses. The important geometric quantity that
describes the fluids’ behavior under stress is the rate of deformation.
To define the deformation of a fluid under acting stresses, first consider motion
in the two-dimensional xy plane. Choose three neighboring points ABC (Figure 1.7.1)
selected to make up a right angle at an initial time t. A is a distance x along the x-axis
from B, and C is a distance y above B along the y-axis.
As the flow evolves through a short time interval t, the angle ABC will change,
as will the distance between the three points. At this later time t +t, these points will
have moved to A
B
, and C
, as shown. Using Taylor series expansions to the first
order, the fluid that initially was at point A will have x and y velocity components
given by v
x
+
v
x
x
x and v
y
+
v
y
x
x. The fluid initially at point A will move a distance
v
x
+
v
x
x
x
t to the right of A, and a distance
v
y
+
v
y
x
x
t above A. Similarly,
the fluid initially occupying point B has moved to point B
—that is, v
x
t to the right
of B and v
y
t above B, and the fluid initially at point C has moved to C
, which is
v
y
+
v
y
y
y
t above C and
v
x
+
v
x
y
y
t to the right of C.
Looking first at the time rate of change of lengths, it is seen that after a time interval
t the rate of change of length along the x-axis per unit length, which will be denoted
by d
xx
, is the final length minus the original length divided by the original length, all
divided by t. In the limit this is
d
xx
=
x +
v
x
+
v
x
x
x
t
−
x +v
x
t
xt
=
v
x
x
(1.7.1)
C
dx
A
B
C′
B′
A′
dy
d θ
2
d θ
1
∂v
x
∂v
x
∂v
y
v
y
dt
(v
x
+
v
x
dt
∂y
dy
)dt
∂v
y
(v
y
+
∂x
dx
)d
t
v
x
+
∂y
dy
∂v
y
v
y
+
∂y
dy
∂v
x
v
x
+
∂x
dx
v
y
+
v
y
v
x
∂x
dx
x
y
Figure 1.7.1 Rates of deformation—two dimensions
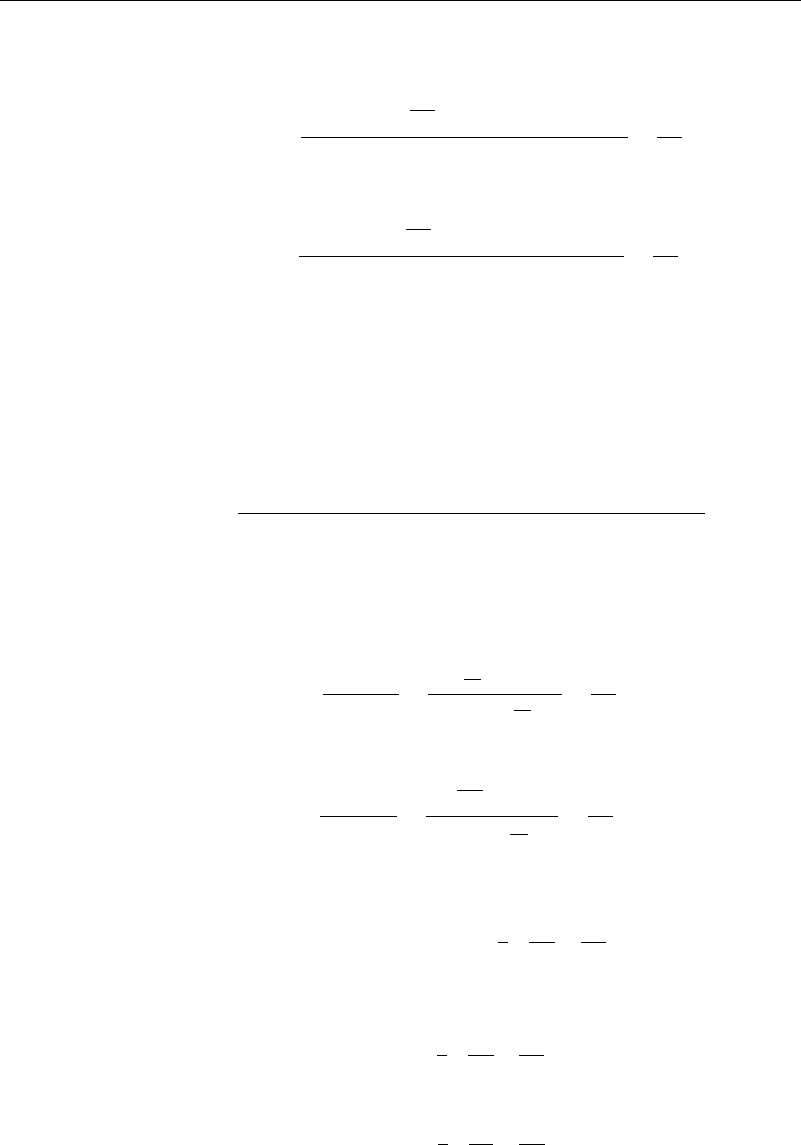
22 Fundamentals
A similar analysis along the y-axis would give the rate of change of length per unit
length as measured along the y-axis, d
yy
,as
d
yy
= lim
t→0
y +
v
y
+
v
y
y
y
t
−
y +v
y
t
yt
=
v
y
y
(1.7.2)
and similarly in the z direction
d
zz
= lim
t→0
z +
v
z
+
v
z
x
z
t
−z +v
z
t
zt
=
v
z
z
(1.7.3)
The d
xx
d
yy
, and d
zz
are the normal rates of deformation and can loosely be thought
of as rates of normal, or extensional, strain. The term “loosely” is used, since the
definitions of strain you might be familiar with from the study of solid mechanics are
for infinitesimal strains. For finite strain, many different definitions are used in solid
mechanics for rates of strain. Since in fluid mechanics strains are always finite—and
also usually very large—using the term “rates of deformation” avoids confusion.
Note that the rate of change of volume per unit volume is the volume at t +t
minus the original volume at t divided by the original volume times t,or
lim
xyzt→0
x +d
xx
xt +d
yy
ytz +d
zz
zt −xyz
xyzt
=d
xx
+d
yy
+d
zz
= ·v
(1.7.4)
This is the dilatational strain rate.
Besides changes of length, changes of angles are involved in the deformation.
Looking at the angles that AB and BC have rotated through, it is seen that
˙
1
≈
tan
−1
1
t
≈
v
y
x
xt
xt1+
v
x
x
t
≈
v
y
x
(1.7.5)
and similarly
˙
2
≈
tan
−1
2
t
≈
v
x
y
yt
yt1+
v
y
y
t
≈
v
x
y
(1.7.6)
The sum of the two angular rates,
˙
1
+
˙
2
, represents the rate of change of the angle
ABC. Let
d
xy
=d
yx
=05
˙
1
+
˙
2
=
1
2
v
y
x
+
v
x
y
(1.7.7)
be defined as the rate of shear deformation as measured in the xy plane. Similarly
define
d
yz
=d
zy
=
1
2
v
y
z
+
v
z
y
(1.7.8)
and
d
zx
=d
xz
=
1
2
v
z
x
+
v
x
z
(1.7.9)
as the rates of shear deformation as measured in the yx and xz planes, respectively.

1.7 Rates of Deformation 23
The one-half factor in the definition of the rate of deformation components is
introduced so that the components transform independent of our selection of axes. Since
the definition of angular rate of deformation is to some degree our option, any choice
that gives a measure of the deformation is suitable. In this case we wish to relate the
deformation rate to stress, and we would like to do it in such a manner that if we change
to another coordinate system, all quantities change correctly.
Therateofdeformationcomponentsthathavebeenarrivedatcanbeshowntotransform
as a second-order tensor. Note that if we interchange the order in which the subscripts
are written in the definitions, there is no change in the various components. That is,
d
xy
=d
yx
d
xz
=d
zx
and d
yz
=d
zy
(1.7.10)
As in the case of the stress tensor, such a tensor is said to be a symmetric tensor.
It may be helpful to your physical understanding of rate of deformation to look at
what is happening from a slightly different viewpoint. Consider any two neighboring
fluid particles a distance dr apart, where the distance dr changes with time but must
remain small because the particles were initially close together. To find the rate at which
the particles separate, take the time derivative of dr, obtaining
Ddr
Dt
=d
Dr
Dt
=dv (1.7.11)
where dv is the difference in velocity between the two points, as shown in Figure 1.7.2.
Since the magnitude of the distance between the two points, or more conveniently its
square, is
dr
2
=dr ·dr, we have
Ddr
2
Dt
=2dr ·
Ddr
Dt
=2dr ·dv
=2dx
v
x
x
dx +
v
x
y
dy +
v
x
z
dz
+2dy
v
y
x
dx +
v
y
y
dy +
v
y
z
dz
+2dz
v
z
x
dx +
v
z
y
dy +
v
z
z
dz
(1.7.12)
=2
v
x
x
dx
2
+
v
y
y
dy
2
+
v
z
z
dz
2
+
v
x
y
+
v
y
x
dxdy +
v
x
z
+
v
z
x
dxdz
+
v
z
y
+
v
y
z
dzdy
=2
d
xx
dx
2
+d
yy
dy
2
+d
zz
dz
2
+2d
xy
dxdy +2d
xz
dxdz +2d
yz
dydz
v + dv
v
v
d
v
dr
Figure 1.7.2 Velocity changes
