Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


334 Appendix
and so for a tensor of any order
Ty = T
ij···
yg
i
yg
j
y =T
ij···
xa
im
g
m
xa
jn
g
n
x
But
Tx = T
ij···
xg
i
xg
j
x
Thus, to have Tx = Ty—that is, to have the tensor independent of the coordinate
system—it is necessary then that the components transform according to
T
mn—
x = a
im
a
jn
—T
ij—
or, multiplying both sides by direction cosines, contracting, and using equation (A.6.5)
several times,
T
ij—
y = a
im
a
jn
—T
mn—
x (A.6.8)
When there are no subscripts (that is, the tensor is a scalar), then the direction cosines
disappear from equation (A.6.8).
To emphasize this transformation law for the orders used the most, we write the
following transformation laws:
Zero order tensor Ty: Tx =Ty (A.6.9)
First order tensor components T
j
y: T
i
x =a
im
T
m
y (A.6.10)
Second order tensor components T
ij
y: T
ij
x =a
im
a
jn
T
mn
y (A.6.11)
Third order tensor components T
ijk
y: T
ijk
x =a
im
a
jn
a
ko
T
mno
y (A.6.12)
For a second-order tensor, if the third axis is not rotated, then
a
i3
=a
3i
=
i3
Then the equation
T
ij
x = a
im
a
jn
T
mn
y i =1 2j= 1 2
is the equation of a circle, called Mohr’s circle. It affords an easy graphical interpretation
of the transformation law in two dimensions.
Tensor components can have symmetry properties. If, for instance, for a second-
order tensor the components obey the rule
T
ij
=T
ji
(A.6.13)
it is said that the second order tensor is symmetric. The Kronecker delta is an example
of a symmetric tensor. If, on the other hand, the components obey the rule
T
ij
=−T
ji
(A.6.14)
it is said that the second order tensor is antisymmetric,orskew symmetric. Any second-
order tensor can be written as the sum of a symmetric part and a skew symmetric
part—that is,
T
ij
=05T
ij
+T
ji
+05T
ij
−T
ji
(A.6.15)
The first two terms are clearly symmetric, and the last two are clearly skew symmetric.
Components of tensors of order higher than two can be symmetric or skew symmetric
in any pair of their indices.

A.6 Tensors in Cartesian Coordinates 335
Example A.6.1 Unit vectors
Show that g
i
x =a
ji
g
j
y, and thus verify equations (A.6.4) and (A.6.6).
Solution. This result is simply the familiar decomposition of a vector into its com-
ponents. In the y-axes, the three unit vectors e
i
x make angles with the axes y
1
y
2
, and
y
3
, whose direction cosines are a
1i
a
2i
, and a
3i
. Applying the decomposition law, the
result follows.
Example A.6.2 Direction cosines
Show by a suitable dot product that the a
ij
are direction cosines of the vectors g
i
y
referred to the g
i
x vectors.
Solution. Taking the dot product g
i
x ·g
j
y and using the results of Example
A.6.1, we have g
i
x ·g
j
y = a
ki
g
k
y ·g
j
y = a
ki
kj
=a
ji
by the orthogonality of the
y-axes. QED.
Example A.6.3 Tensor properties of the Kronecker delta and alternating tensors
Show that the alternating tensor and the Kronecker delta are tensors in a Cartesian
coordinate system.
Solution. Assume that the Kronecker delta is a second-order tensor. From the trans-
formation law for its components equation (A.6.11),
ij
x =a
im
a
jn
mn
y
From the summation property of the Kronecker delta,
ij
x =a
im
a
jn
mn
y =a
im
a
jm
=
ij
x
Thus, the transformation law is valid.
Assume that the alternating tensor is a third-order tensor. From the transformation
law for its components equation (A.6.12),
e
ijk
x =a
im
a
jn
a
kp
e
mnp
y
By expansion of both sides, it is seen that
a
im
a
jn
a
kp
e
mnp
y =e
ijk
y times the determinant of a.
By the orthogonality of the axes, the determinant of the direction cosines is one. Thus,
e
ijk
x =e
ijk
y
and the transformation law is valid.
Besides the inherent invariant property of a tensor, tensor components also possess
invariant properties. For instance, A
i
A
i
is the same in any coordinate system, as can be
easily seen in equation (A.6.6) and in fact is the square of the magnitude of the vector
A. This is the only independent invariant that can be formed for a first-order tensor. For
a second-order tensor, there are at most three independent invariants:
T
ii
=I
T
(A.6.16)

336 Appendix
05I
2
T
−T
ij
T
ji
=II
T
(A.6.17)
determinate of T
ij
=III
T
(A.6.18)
That these are invariants can be shown through use of the transformation laws.
Example A.6.4 Invariants
Verify that equation (A.6.9) is invariant under rotation of axes.
Solution. To do this, we use the transformation of components relation (equation
(A.6.11))—that is,
T
ij
x =a
im
a
jn
T
mn
y Then
T
ii
x =T
11
x +T
22
x +T
33
x =a
1m
a
1n
T
mn
y +a
2m
a
2n
T
mn
y +a
3m
a
3n
T
mn
y
=
a
1m
a
1n
+a
2m
a
2n
+a
3m
a
3n
a
1p
a
1q
+a
2p
a
2q
+a
3p
a
3q
T
pq
y
=a
ip
a
iq
T
pq
y
T
ij
x =a
im
a
jn
T
mn
y Then
T
ii
x =T
11
x +T
22
x +T
33
x =a
1m
a
1n
T
mn
y +a
2m
a
2m
T
mn
y +a
3m
a
3n
T
mn
y
=
a
1m
a
1n
+a
2m
a
2n
+a
3m
a
3n
T
mn
y =a
im
a
in
T
mn
y
T
ij
x =a
im
a
jn
T
mn
y Then
T
ii
x =T
11
x +T
22
x +T
33
x =a
1m
a
1n
T
mn
y +a
2m
a
2n
T
mn
y +a
3m
a
3n
T
mn
y
=
a
1m
a
1n
+a
2m
a
2n
+a
3m
a
3n
T
mn
y =a
im
a
in
T
mn
y
But from equation (A.6.6),
a
im
a
in
=
mn
T
ii
x =
mn
T
mn
y =T
mm
y ThusT
ii
x =T
ii
y =I
T
From the preceding result, to prove 05I
2
T
−T
ij
T
ji
= II
T
is invariant, we need only
show that
T
ij
xT
ji
x =T
ij
yT
ji
y
Using equation (A.6.11), we have
T
ij
xT
ji
x =a
im
a
jn
T
mn
ya
jp
a
iq
T
pq
y
=a
im
a
iq
a
jn
a
jp
a
iq
T
mn
yT
pq
y after rearranging
=
mq
np
T
mn
yT
pq
y using equation A66
=T
qn
yT
nq
y.
This is the desired result.
For the third result, we note from writing out the result in detail that
determinate of T
ij
x =
T
11
T
12
T
13
T
21
T
22
T
23
T
31
T
32
T
33
=
e
ijk
e
pqr
T
ip
T
jq
T
kr
6
Using the transformation law (equation (A.6.11)),

A.7 Tensors in Orthogonal Curvilinear Coordinates 337
e
ijk
e
pqr
T
ip
xT
jq
xT
kr
x
=e
ijk
e
pqr
a
is
a
pt
T
st
ya
ju
a
qv
T
uv
ya
kw
a
rz
T
wz
y
=e
ijk
e
pqr
a
is
a
pt
a
ju
a
qv
a
kw
a
rz
T
st
yT
uv
yT
wz
y.
As can be seen by writing out both sides,
e
ijk
a
is
a
ju
a
kw
=e
suw
determinant of a and
e
pqr
a
pt
a
q
var z =e
tvz
determinant of a
But the determinant of a is one, since the coordinates are orthogonal. Then
e
ijk
e
pqr
T
ip
xT
jq
xT
kr
x =e
suw
e
tvz
T
st
yT
uv
yT
wz
y
=e
suw
e
suw
times the determinant of Ty
=6 times the determinant of Ty
that is the desired result.
That there are at most three invariants of a second-order tensor follows from the
Cayley-Hamilton theorem. This theorem states that the products of components of a
tensor are related by
T
im
T
mn
T
nj
−I
T
T
im
T
mj
+II
T
T
ij
−III
T
T
ij
=0. (A.6.19)
Proof of the Cayley-Hamilton theorem is as follows. By contraction (letting i equal j
and summing),
T
im
T
mn
T
ni
=I
T
II
T
=I
T
I
2
T
−2II
T
−II
T
I
T
+3III
T
=I
3
T
−3I
T
II
T
+3III
T
(A.6.20)
Premultiplication of equation (A.6.10) by T
jk
or higher powers of T with the implied
contraction shows the desired result. When there is only one subscript, equation (A.6.8)
is the familiar form for the decomposition of a vector. When there are two subscripts,
equation (A.6.8) is the three-dimensional generalization of Mohr’s circle.
A.7 Tensors in Orthogonal Curvilinear Coordinates
The mathematics of tensors in orthogonal curvilinear coordinates is only a bit more
complicated than that in Cartesian coordinates, although the application of the general
results to a particular coordinate system can be tedious. In the following, we use
orthogonal coordinate systems with coordinate axes y
1
y
2
y
3
and with orthogonal base
vectors
g
i
=ds/dy
i
(A.7.1)
where ds is an elemental distance. Define
h
1
=
√
g
1
·g
1
h
2
=
√
g
2
·g
2
h
3
=
√
g
3
·g
3
(A.7.2)
so that the distance between two infinitesimally distant points is
ds
2
=h
1
dy
1
2
+h
2
dy
2
2
+h
3
dy
3
2
(A.7.3)

338 Appendix
It is usually easier to use equation (A.5.4) to find the hs than equation (A.5.3) for a
particular coordinate system.
The gradient and Laplacian of a vector are given by
grad = =
1
h
1
x
1
1
h
2
x
2
1
h
3
x
3
(A.7.4)
2
=
1
h
1
h
2
h
3
x
1
h
2
h
3
h
1
x
1
+
x
2
h
3
h
1
h
2
x
2
+
x
3
h
1
h
2
h
3
x
3
(A.7.5)
The divergence of a vector is given by
div V = ·V =
1
h
1
h
2
h
3
h
2
h
3
V
1
x
1
+
h
3
h
1
V
2
x
2
+
h
1
h
2
V
3
x
3
(A.7.6)
The curl of a vector is given by
curl V = ×V =
1
h
2
h
3
h
3
V
3
x
2
−
h
2
V
2
x
3
i +
1
h
3
h
1
h
1
V
1
x
3
−
h
3
V
3
x
1
j
(A.7.7)
+
1
h
1
h
2
h
2
V
2
x
1
−
h
1
V
1
x
2
k
Equations (A.7.6) and (A.7.7) are useful in expressing the continuity equation and
the vorticity vector in orthogonal curvilinear coordinates, and equation (A.7.5) for the
continuity equation for an irrotational flow. For the rate of deformation the expressions
for the tensor components are
d
11
=
1
h
1
v
1
x
1
+
v
2
h
2
h
1
h
2
+
v
3
h
3
h
1
h
3
d
22
=
1
h
2
v
2
x
2
+
v
3
h
3
h
2
h
3
+
v
1
h
1
h
2
h
1
d
33
=
1
h
3
v
3
x
3
+
v
1
h
1
h
3
h
1
+
v
2
h
2
h
3
h
2
2d
12
=2d
21
=
h
3
h
2
x
2
v
3
h
3
+
h
2
h
3
x
3
v
2
h
2
2d
23
=2d
32
=
h
1
h
3
x
3
v
1
h
1
+
h
3
h
1
x
1
v
3
h
3
2d
31
=2d
13
=
h
2
h
1
x
1
v
2
h
2
+
h
1
h
2
x
2
v
1
h
1
.
(A.7.8)
The stress components are given by
11
=−p +
·v +2d
11
22
=−p +
·v +2d
22
33
=−p +
·v +2d
33
(A.7.9)
12
=
21
=2d
12
23
=
32
=2d
23
31
=
31
=2d
31
or in index notation
ij
=−p +
·v
ij
+2d
ij

A.7 Tensors in Orthogonal Curvilinear Coordinates 339
The acceleration is arrived at by first writing the convective terms in a correct
vector form. As can be verified by writing out the components in Cartesian coordinates
and comparing, that form is
v ·v =−v× ×v +05
v
2
=−v×curl v +05grad
v
2
. (A.7.10 )
The first term on the right is found in an arbitrary orthogonal system by applying
equation (A.7.7), the second by use of equation (A.7.4).
The continuity equation is given by
t
+
1
h
1
h
2
h
3
h
2
h
3
v
1
y
1
+
h
3
h
1
v
2
y
2
+
h
1
h
2
v
3
y
3
=0 (A.7.11)
Since the Navier-Stokes equations involve taking the second derivative of a vector,
necessary for the viscous terms, the procedure is much longer and more tedious than for
the continuity equation or the Laplace equation. The acceleration terms can be found
from equation (A.7.10), and the pressure gradient from equation (A.7.4). The remaining
terms involve the operation
2
v. Writing this out is a long process and would require
several pages of equations. Instead, note that
2
v = ·v − ×
×v
(A.7.12)
and equations (A.5.7) and (A.5.8) tell us how to compute the divergence and curl. The
Navier-Stokes equations then are of the form
v
t
−v × +
1
2
v
2
=−p +g +
·v − ×
(A.7.13)
To illustrate the previous, consider the next two familiar coordinate systems.
A.7.1 Cylindrical Polar Coordinates
The element of length in this coordinate system is
ds
2
=dr
2
+rd
2
+dz
2
with
y
1
y
2
y
3
=r z.
The polar coordinates are expressed in terms of Cartesian coordinates by r =
x
2
1
+x
2
2
= tan
−1
x
2
/x
1
z=x
3
Comparing equation (A.7.10) with equation (A.7.3), we see that h
1
=h
3
=1h
2
=
y
1
=r. Then
2
=
1
r
r
r
r
+
1
r
2
2
2
+
2
z
2
(A.7.14)
·V =
1
r
rV
r
r
+
1
r
V
+
V
z
z
(A.8.15)
×V =
1
r
V
z
−
V
z
e
r
+
V
r
z
−
V
z
r
e
+
1
r
rV
r
−
V
r
e
z
(A.8.16)

340 Appendix
d
rr
=
u
r
d
=
1
r
v
+
u
r
d
zz
=
w
z
2d
r
=2d
r
=r
r
v
r
+
1
r
u
2d
rz
=2d
zr
=
u
z
+
w
r
2d
z
=2d
z
=
1
r
w
+
v
z
(A.8.17)
r
2
=x
2
+y
2
= tan
−1
y
x
z=z
The continuity equation is then
t
+
1
r
ru
r
+
1
r
v
+
w
r
=0 (A.7.18)
The Navier-Stokes equations for constant density and viscosity are
u
t
+u
u
r
+
v
r
u
+w
u
z
−
v
2
r
2
=−
p
r
+g
r
+
2
u −
u
r
2
−
2
r
2
v
v
t
+u
v
r
+
v
r
v
+w
v
z
+
uv
r
2
=−
1
r
p
+g
+
2
v −
v
r
2
+
2
r
2
u
(A.7.19)
w
t
+u
w
r
+
v
r
w
+w
w
z
=−
p
z
+g
+
2
w
where the Laplacian
2
is as given in equation (A.8.11) and u v w =v
r
v
v
z
.
A.7.2 Spherical Polar Coordinates
The element of length in this coordinate system is
ds
2
=dR
2
+Rd
2
+R sin d
2
with y
1
y
2
y
3
=R and so
h
1
=1h
2
=y
1
=R h
3
=y
1
sin y
2
=R sin .
In terms of Cartesian coordinates, R
2
=x
2
1
+x
2
2
+x
2
3
=cos
−1
x
3
R
=tan
−1
x
2
x
. Then
=
R
e
R
+
1
R
e
+
1
R sin
e
(A.7.20)
2
=
1
R
2
R
R
2
R
+
1
R
2
sin
sin
+
1
R
2
sin
2
2
2
(A.7.21)
·v =
1
R
2
R
2
u
R
+
1
R sin
v sin
+
1
R sin
w
(A.7.22)
×v =
1
R sin
w sin
−
v
e
R
+
1
R sin
u
−
wR sin
R
e
+
1
R
Rv
R
−
u
e
(A.7.23)
d
RR
=
u
R
d
=
1
R
v
+
u
R
d
=
1
R sin
w
+
u
R
+
v cot
R
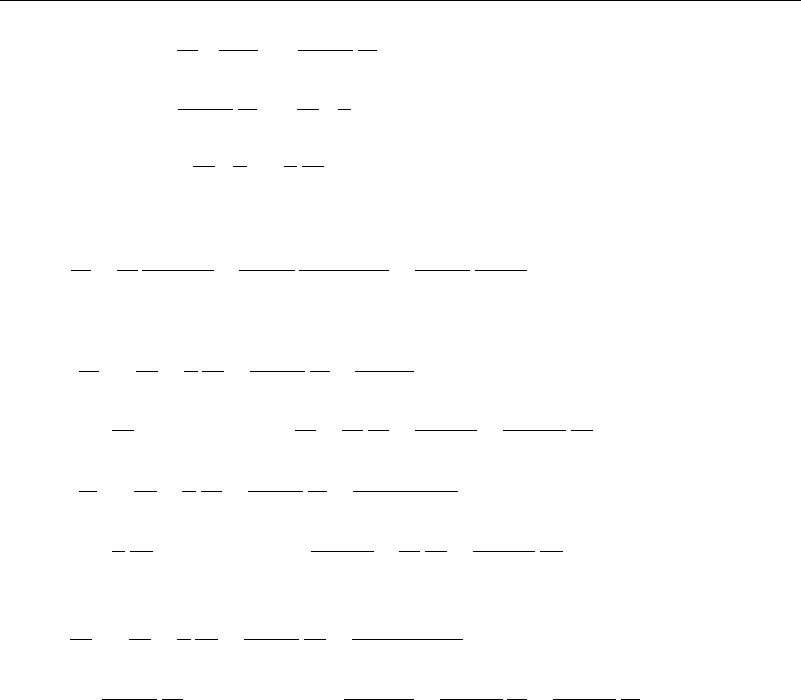
A.8 Tensors in General Coordinates 341
2d
=2d
=
w
sin
+
1
R sin
v
2d
R
=2d
R
=
1
R sin
u
+R
R
w
R
(A.7.24)
2d
R
=2d
R
=R
R
v
R
+
1
R
u
The continuity equation is given by
t
+
1
R
2
R
2
u
R
+
1
R sin
v sin
+
1
R sin
w
=0 (A.7.25)
The Navier-Stokes equations for constant density and viscosity are
u
t
+u
u
R
+
v
R
u
+
w
R sin
u
−
v
2
+w
2
R
2
=−
p
R
+g
R
+
2
u −
2u
R
2
−
2
R
2
v
−
2v cot
R
2
−
2
R
2
sin
w
v
t
+u
v
R
+
v
R
v
+
w
R sin
v
+
uv −w
2
cot
R
2
=−
1
R
p
R
+g
+
2
v −
v
R
2
sin
+
2
R
2
u
−
2 cot
R
2
sin
w
(A.7.26)
w
t
+u
w
R
+
v
R
w
+
w
R sin
w
+
uw +vw cot
R
2
=−
1
R sin
p
+g
+
2
w −
w
R
2
sin
2
+
2
R
2
sin
u
+
2 cot
R
2
sin
v
where the Laplacian
2
is as given in equation (A.8.19) and u v w =v
R
v
v
.
A.8 Tensors in General Coordinates
In Cartesian coordinates, dealing with tensors is particularly simple because the base
vectors are constants and thus for a vector (as an example)
V = V
j
g
j
(A.8.1)
In general coordinates, the base vectors vary from point to point, and when differentiating
a tensor, the base vectors have to be differentiated as well. This leads to greater
complications than might at first be expected, since more than one set of base vectors
can be defined and their direction cosines will generally differ. One starts to deal
with what are called contravariant and covariant base vectors and tensor components,
depending on the type of base vector that is used. Further, the various tensor components
and base vectors will generally differ in their physical dimensions. (For example, in
cylindrical polar coordinates two of the covariant components of the velocity vector will
have dimensions of length/time, while the third will have dimensions of just reciprocal
time.) In our work, we are interested in dealing with the physical components—that

342 Appendix
is, components that all have the same physical dimensions. Unfortunately, physical
components do not obey the simple transformation laws of tensors.
The starting point for a study of general tensors is geometry. As in studying rates of
deformation, consider two adjacent points separated by a vector distance dr. (Boldface
will be used to denote both vectors and tensors of higher order.) If we have a coordinate
system x
1
x
2
x
3
, we can write
dr =
r
x
i
dx
i
(A.8.2)
This implies that the vectors r/x
i
are locally tangent to the x coordinate system. So
a good choice for base vectors tangent to our coordinate system is
g
i
=
r
x
i
(A.8.3)
Since the magnitude ds of the distance between the two neighboring points is
given by
ds
2
=dr ·dr =g
i
dx
i
·g
j
dx
j
=g
i
·g
j
dx
i
dx
j
=g
ij
dx
i
dx
j
(A.8.4)
the g
ij
given by g
ij
= g
i
·g
j
is suitable as the covariant components of the symmetric
metric tensor. Depending on the coordinate system, the dimensions of the various g
ij
components can vary. In spherical polar coordinates, for instance, one has dimensions
of length, while two are dimensional.
Returning to equation (A.8.4), we could have written
ds
2
=
s
x
i
s
x
j
dx
i
dx
j
(A.8.5)
Comparison with equation (A.8.4) implies that an alternate definition of the covariant
metric tensor components is
g
ij
=
s
x
i
s
x
j
(A.8.6)
If we introduce a second coordinate system y at the same point we are considering,
notice that using the product rule of calculus, we can write
dr = g
i
xdx
i
=
r
x
i
x
i
y
j
dy
j
=g
j
ydy
j
Thus,
g
j
y =
x
i
y
j
g
i
x (A.8.7)
This is the transformation law for covariant components of a vector. In general, the
transformation law for covariant components of a tensor of order n is given by
A
···
y =
x
i
y
x
j
y
x
k
y
···A
ijk···
x (A.8.8)
where there are n subscripts on the A and n partial derivatives. The partial derivatives
act like direction cosines.
We have assumed here that a metric measuring the distance between two neigh-
boring points exists in our space. Such a space is called a Riemannian space. Also,

A.8 Tensors in General Coordinates 343
our discussion is limited to three-dimensional spaces. Nonmetric spaces exist, but their
applicability to fluid mechanics is doubtful. Generalization to higher dimensions is
trivial.
Contravariant base vector components can also be defined using cross-products and
the alternating tensor. Letting
g
i
×g
j
=e
ijk
g
k
(A.8.9)
this definition serves the purpose of having the new base vectors orthogonal to the old,
but they will not necessarily be tangent to the coordinate system. Equation (A.8.10) can
be solved to explicitly give the contravariant base vectors as
g
1
=g
2
×g
3
/
√
g g
2
=g
3
×g
1
/
√
g g
3
=g
1
×g
2
/
√
g
where
√
g =g
1
·
g
2
×g
3
g=detg
ij
(A.8.10)
In a manner similar to that just used, the components of the symmetric conjugate metric
tensor are defined by
g
ij
=g
i
·g
j
(A.8.11)
The general transformation law for contravariant components is given by
A
···
y =
y
x
i
y
x
j
y
x
j
···A
ij k···
x (A.8.12)
What is the relationship between the contravariant and covariant tensor components?
With g denoting the determinant of g
ij
as previously, let
ij
denote the cofactor of g
ij
.
From equation (A.8.10) we have g
ij
=
ij
/g,so
g
ij
g
jk
=g
ij
jk
/g =
k
i
(A.8.13)
where the are the components of the Kronecker delta. Thus, the contravariant gs play
the role of the inverse of the covariant gs. It can be shown in a similar fashion that
g
i
=g
ij
g
j
and g
i
=g
ij
g
j
(A.8.14)
The metric tensors can also be used to raise and lower indices. Since it can be
shown from the transformation laws that V = V
i
g
i
=V
i
g
i
, it follows that
V
i
=g
ij
V
j
and V
i
=g
ij
V
j
(A.8.15)
Similarly for a second-order tensor,
V
ij
=g
ik
g
jl
V
kl
and V
ij
=g
ik
g
jl
V
kl
(A.8.16)
and so on for higher-order tensors. Mixed components could also be introduced by
operations such as
V
k
i
=g
il
V
lk
and V
i
k
=g
jl
V
kl
(A.8.17)
Notice that in all of the preceding, the superscripts are the same on both sides of
the equals sign, as are the subscripts. This must always be true for the equation to be
valid. For example, the invariants used in the Cayley-Hamilton theorem for second-order
symmetric tensors in general coordinates are
I =A
i
i
II=
1
2
A
ij
A
ji
−I
2
III =
1
6
2A
i
j
A
j
k
A
k
i
−3A
i
j
A
j
i
I +I
3
=det
A
i
j
