Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


274 Computational Methods—Ordinary Differential Equations
In this example, the approximating functions have been chosen to be linear. This
may be adequate in many cases. If not, higher-order polynomials or other functions may
be used that cover the interval in a similar fashion.
11.5 Linear Stability Problems—Invariant Imbedding and
Riccati Methods
In Chapter 9 several flow stability problems were considered—namely, Rayleigh-
Bénard, Couette and Poiseuille viscous flows, and several interfacial-wave-type prob-
lems for inviscid flows. With the exception of the Rayleigh-Bénard convection flows,
all of the viscous flow problems involved rather serious and sophisticated computa-
tions, even though the equations were linear and therefore traditional series expansion
methods and superposition could be used. When numerical methods are considered,
however (sometimes surprisingly), there is no advantage to having linear equations, and
exchanging them for nonlinear equations may have some advantage.
To introduce the concept of invariant imbedding, consider a very simple equation
that often appears when discussing mechanical problems (the Euler column theory is
one example):
d
2
y
dx
2
+
2
y =0y0 =y1 = 0 (11.5.1)
This is a classic eigenvalue (characteristic value) problem with eigenvalues , where
the solution is zero unless takes on the values = n n = 1 2 3. In that case
the solution is yx =A sinx, where A is indeterminate.
If equation (11.5.1) is changed to
d
2
y
dx
2
+
2
y =1y0 = y1 =0 (11.5.2)
the solution becomes determinate, with the solution
yx =
1
2
1−cosx +
−1+cos
sin x
sin
(11.5.3)
This is a well-behaved solution as long as does not equal one of the eigenvalues
associated with the homogeneous problem (11.5.)!
Similarly, if equation (11.5.1) had been changed to
d
2
y
dx
2
+
2
y =0y0 =0y1 = 1 (11.5.4)
the solution would be
yx =
sin x
sin
(11.5.5)
Thus, either change from the homogeneous problem, whether it be in the differential
equation or the boundary conditions, results in a solution that is well defined except
when is one of the eigenvalues.
Of the two techniques of the section title, the Riccati method is the easiest to describe.
Start with equation (11.5.1) and let
dy
dx
= Rxy. Then
d
2y
dx
2
=
dR
dx
y +R
dy
dx
=
dR
dx
+R
2
y.

11.5 Linear Stability Problems—Invariant Imbedding and Riccati Methods 275
The second derivative of y is known from equation (11.5.1). Thus,
d
2
y
dx
2
=−
2
y =
dR
dx
+R
2
y, or, upon dividing by y, the result is
dR
dx
=−
2
−R
2
(11.5.6)
For later reference, note that in this simple case, equation (11.5.6) can be integrated to
give
Rx =
cosx
sin x
(11.5.7)
Equation (11.5.6) falls in the general form of what is termed a Riccati equation.
(The general form of a Riccati equation is R
=A +BR +RC +RDR, where R can be a
vector and A, B, C, D square matrices.) It is nonlinear and ideally suited to a numerical
method of integration such as Runge-Kutta.
To start the integration, the value of R at x = 0 is needed. From the boundary
conditions, since y is to be set to zero and its derivative must be nonzero, it is seen
that R0 is singular. This can be gotten around in at least two ways. First, looking at
equation (11.5.6), notice that when R and its derivative are large, then
dR
dx
−R
2
,so
with a little imagination it can be concluded that R behaves like 1/x at the origin.
Alternately, we can work with the reciprocal (more generally, the inverse) of R,
letting S = 1/R, so that
dS
dx
=−
1
R
2
dR
dx
=−
1
R
2
−
2
−R
2
= 1 +
2
S
2
.IfR is infinite at
the origin, S will be zero there, so the integration can proceed.
To do so, however, a value for must be set first. Choose an arbitrary value that
seems in a reasonable range, and then carry out the integration until R becomes infinity
(defined here as being outside the bounds of numbers your computer is capable of
handling). Then this value where R becomes infinite is the length at which the chosen
value of is the correct eigenvalue. Thus, the problem has been turned around, finding
the value of the spacing associated with an eigenvalue rather than the usual reverse
of this.
One thing to note is that while S is finite throughout most of the region of integration,
it probably will be infinite at an intermediate point. (From equation (11.5.7), we can
see that this is true at x = /2.) Thus, programming requires that we start with the S
equation, then shift to the R equation, then (to improve accuracy) shift back to the S
equation as the singularity in R is approached. To accomplish this, fortunately, does not
require particularly skilled programming abilities.
The invariant imbedding technique follows very closely the Riccati approach. It
recognizes that the value of the eigenvalue ( in this case) depends on the length and
along the lines of equation (11.5.4) changes equation (11.5.1) to
2
yx z
x
2
+
2
yx z = 0y0z=0 yz z =1 (11.5.8)
R is chosen as Rz = yz z/z, differentiation of R with respect to z and using
equation (11.5.6) to eliminate the derivative, leads to an equation practically identical
to equation (11.5.6).
In the problem considered here, there is not much flexibility in the choice of R.
In higher-order differential systems, depending on the boundary conditions, it may be
possible to avoid having to deal with singularities and the need to invert R.
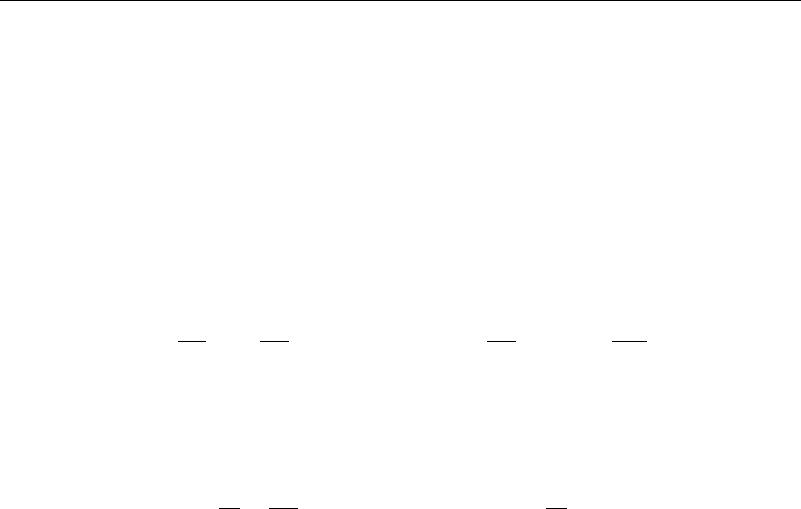
276 Computational Methods—Ordinary Differential Equations
These methods have been successfully used in computing the neutral stability
curves for Couette-Taylor stability (Curl and Graebel, 1972; Wilks and Sloan, 1976),
for Poiseuille flow between parallel plates (Curl and Graebel, 1972; Davey, 1977;
Sloan, 1977) and for the Blasius flat plate solution (Wilks and Bramley, 1977). They are
at least as accurate as previous methods (Orszag, 1971) and (perhaps even better) easier
to use.
To illustrate the method for more complex flows, consider the Orr-Sommerfeld
equation for plane Poiseuille flow. Taking the origin at y = 0, the primary flow is
given by U =U
max
1−y
2
, where U
max
is the centerline velocity and y has been made
dimensionless by the half-spacing of the plates. First, recall equation (9.4.8) in the
expanded form
d
4
v
dy
4
−2k
2
d
2
v
dy
2
+k
4
v = ikR
U −c
d
2
v
dy
2
−k
2
v
−v
d
2
U
dy
2
(9.4.8)
To simplify the notation, the primes have been dropped and replaced by y.
Only disturbances of u even in y will be considered, as they are known to be less
stable. By the continuity relation, disturbances even in u are odd in v—thus,
dv
dy
=
d
3
v
dy
3
=0aty = 0 and u =v =
dv
dy
=0aty = 1
Following Davey (1977), let
Z
1
=v Z
3
=v
−k
2
v
Z
2
=v
Z
4
=v
−k
2
v
(11.5.9)
and
Z
2
Z
4
=
R
1
R
2
R
3
R
4
Z
1
Z
3
(11.5.10)
From the boundary conditions at y = 0Z
2
and Z
4
are both zero at y =0. Since Z
1
and
Z
3
are not necessarily zero there, all of the Rs must be set to zero at y = 0. Since Z
1
and Z
2
must both be zero at y =1R
2
=0aty = 1.
Next, differentiate the first of equation (11.5.10),
Z
2
=R
1
Z
1
+R
2
Z
3
(11.5.11)
obtaining
Z
2
=R
1
Z
1
+R
1
Z
1
+R
2
Z
3
+R
2
Z
3
(11.5.12)
where here primes denote derivatives with respect to y. From equation (11.5.9) note
that
Z
1
=v
=Z
2
Z
2
=v
=Z
3
−k
2
Z
1
Z
3
=Z
4
(11.5.13)

11.5 Linear Stability Problems—Invariant Imbedding and Riccati Methods 277
so equation (11.5.12) can be rewritten as
Z
2
=Z
3
+k
2
Z
1
=R
1
Z
1
+R
1
Z
2
+R
2
Z
3
+R
2
Z
4
(11.5.14)
Z
2
and Z
4
can be eliminated from equation (11.5.14) by using equation (11.5.10), which,
upon collection of terms, gives
Z
1
R
1
+R
2
1
+R
2
R
3
−k
2
+Z
3
R
2
+R
1
R
2
+R
2
R
4
−1
=0 (11.5.15)
From equation (9.4.8), the fourth derivative of v is given by
v
=2k
2
v
−k
4
v +ik Re
U −c
v
−k
2
v
−
d
2
U
dy
2
v
or equivalently
v
=2k
2
Z
3
+k
4
Z
1
+ik Re
U −c
Z
3
−
d
2
U
dy
2
Z
1
(11.5.16)
Repeating the previous procedure with the second equation of (11.5.2) and using equation
(11.5.16) gives
Z
1
R
3
+R
1
R
3
+R
3
R
4
−2ik Re
+Z
3
R
4
+R
2
R
3
+R
2
4
−k
2
−ik Re
1−y
2
−c
=0
(11.5.17)
Equations (11.5.15) and (11.5.17) are two homogeneous equations in the two
unknowns Z
1
and Z
3
which must hold over a range of y. The conclusion is then that
the coefficients of Z
1
and Z
3
must vanish, leading to the system of four differential
equations
R
1
=−R
2
1
−R
2
R
3
+k
2
R
2
=−R
1
R
2
−R
2
R
4
+1
R
3
=−R
1
R
3
−R
3
R
4
+2ik Re
R
4
=−R
2
R
3
−R
2
4
+k
2
+ik Re
1−y
2
−c
(11.5.18)
These are the Riccati equations associated with the problem.
Notice that the second and third equations are the same except for the magnitude
of the constant. Thus,
R
3
=2ik Re R
2
(11.5.19)
The procedure requires that values of the wave number, Reynolds number, and the wave
speed be set a priori. Integration then precedes until R
2
= 0, or at least nearly zero. If
the initial guess is close to a true eigenvalue, then this will occur near to 1. Using the
dimensions of the various quantities, once the location of the eigenvalue is known, it is
possible to correct the starting parameters to make the zero occur at 1. Since integration
is in the complex plane, it is entirely possible that a zero of R
2
will not be found for a
particular choice of the three input parameters. It is best to start near known results and
make small steps away from them. A discussion of dealing with more general problems
using the Riccati method is given in the Appendix.
Program 11.5.1 illustrates one realization of a program for this problem. Table 11.5.1
suggests several combinations of input data near the minimum Reynolds number.

278 Computational Methods—Ordinary Differential Equations
PROGRAM Orr
COMPLEX :: R(3)
DIMENSION AMR(3)
DY=.001
Y=0.
DO I=1,3
R(I)=0.
END DO
R2R=0.
R2I=0.
R2ROLD=.00001
WRITE(*,*)
WRITE(*,*) " Solves the Orr-Sommerfeld equation using a Riccati method and also"
WRITE(*,*) " using a 4th order Runge-Kutta scheme."
WRITE(*,*)
WRITE(*,*) " Enter the real part of the wave speed c. "
READ (*,*) C
WRITE(*,*) " Enter the wave number k. "
READ (*,*) AK
WRITE(*,*) " Enter the Reynolds number Re. "
READ (*,*) Re
WRITE(*,*)
WRITE(*,*) " y R(1) R(2) R(3) R(2)real R(2)imag"
WRITE(*,100) Y,AMR(1),AMR(2),AMR(3),R2R,R2I
DO I=1,1050
Y=Y+DY
CALL RK4(R,AK,C,DY,Re,Y)
DO J=1,3
AMR(J)=ABS(R(J))
END DO
R2R=REAL(R(2))
R2I=AIMAG(R(2))
WRITE(*,100) Y,AMR(1),AMR(2),AMR(3),R2R,R2I
IF((R2R*R2ROLD)<0.) THEN
RN=RE*(Y**3)
CN=(C-1.+Y**2)/Y**3
YN=Y+R2R*DY/(R2ROLD-R2R)
R2RS=R2R
R2IS=R2I
END IF
R2ROLD=R2R
END DO
WRITE(*,*)
WRITE(*,*) " Input c, k, Re: ",C,AK,Re
WRITE(*,*) " Computed y, c, k, Re: ",YN,CN,AK,RN
WRITE(*,*) " R(2) real, imaginary: ",R2RS,R2IS
WRITE(*,*)
100 FORMAT(6(F12.7,','))
END PROGRAM
!==================================================
! Runge_Kutta solver - Press, Flannery, et al
!==================================================
SUBROUTINE RK4(R,AK,C,DY,RE,Y)
COMPLEX :: R(3),RT(3),DR(3),DRM(3),DRT(3)
DYH=0.5*DY
YH=Y+DYH
YPH=Y+DY
CALL DERIVS(R,DR,AK,C,RE,Y)
DO I=1,3
RT(I)=R(I)+DYH*DR(I)
END DO ! 11
CALL DERIVS(RT,DRT,AK,C,RE,YH)
DO I=1,3
RT(I)=R(I)+DYH*DRT(I)
END DO ! 12
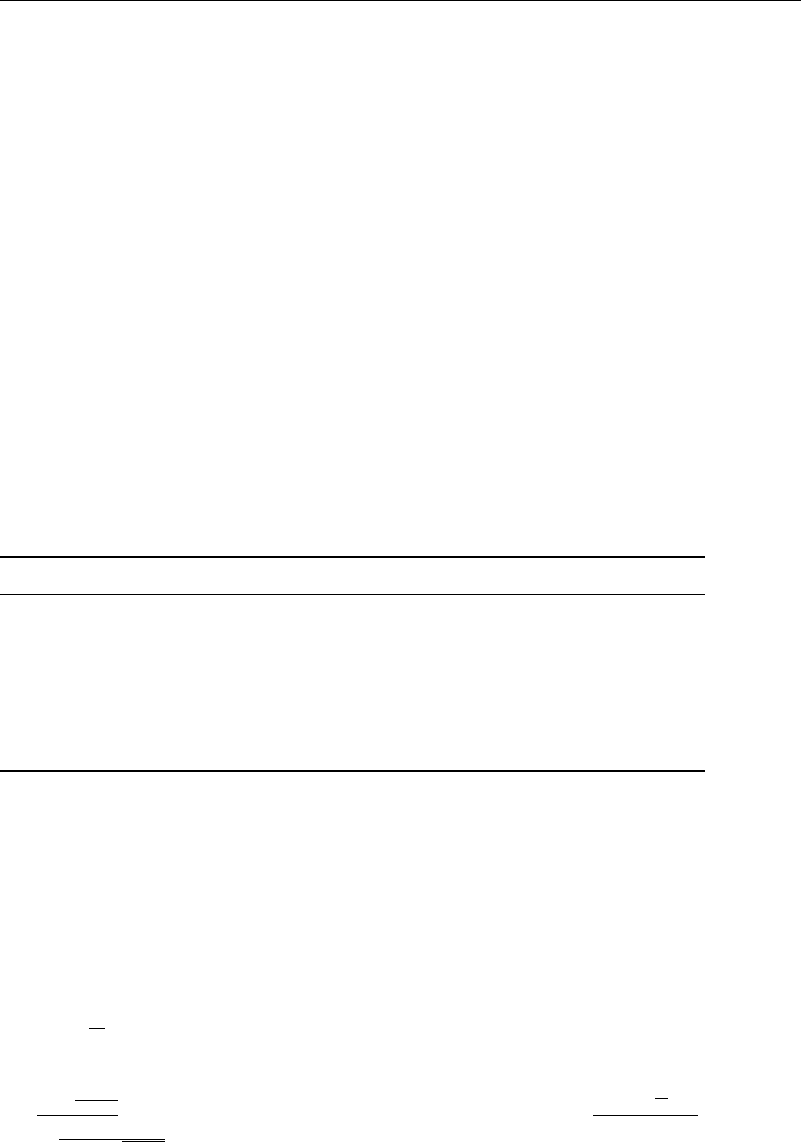
Program 11.5.1—Neutral stability curves for the Orr-Sommerfeld equation (program by the author, subroutine
from Press, Flannery, et al. (1986))
11.6 Errors, Accuracy, and Stiff Systems 279
CALL DERIVS(RT,DRM,AK,C,RE,YH)
DO I=1,3
RT(I)=R(I)+DY*DRM(I)
DRM(I)=DRT(I)+DRM(I)
END DO ! 13
CALL DERIVS(RT,DRT,AK,C,RE,YPH)
DO I=1,3
R(I)=R(I)+DY*(DR(I)+DRT(I)+2.*DRM(I))/6.
END DO ! 14
RETURN
END SUBROUTINE
!===================================================
! Defines equations
!===================================================
SUBROUTINE DERIVS(R,DR,AK,C,RE,Y)
COMPLEX :: AI,R(3),DR(3)
AI=CMPLX(0.,1.)
! R(3)=2*I*K*Re*R(2)
DR(1)=-R(1)*R(1)-R(2)*(2.*AI*AK*RE*R(2))+AK**2
DR(2)=-R(1)*R(2)-R(2)*R(3)+1.
DR(3)=-R(2)*(2.*AI*AK*RE*R(2))-R(3)*R(3)+AK**2+AI*AK*RE*(1.-Y**2-C)
RETURN
END SUBROUTINE
Program 11.5.1—(Continued)
TABLE 11.5.1 Values of Re, k, and c near the minimum Reynolds number
Re kc Re kc
57739761 10163 02634788 57720947 10203 02639588
5773728 10168 02635388 57719966 10205564 02639906
57732251 10173 02635988 57720869 10205617 0 2639905
57729077 10178 02636588 57720879 10205617 02639905
57726406 10183 02637188 57720908 10208 02640188
57724238 10188 02637788 57724077 10209 02640288
57722617 10193 02638388 57720591 102056 02639905
57721499 10198 02638988
11.6 Errors, Accuracy, and Stiff Systems
There are many issues that affect computations made with computers. Computers can
deal only with a finite number of digits when making computations, usually some
multiple of 8, depending on the computer and the program. This means that truncation
errors naturally occur during an operation, as well as round-off errors. These errors
can sometimes be minimized by avoiding the operation of subtraction and also by
minimizing the numbers of operation. If the error introduced by one round-off is ,
after N operations you might be lucky and find that the accumulated error is of the
order of
√
N, providing that the errors accumulated randomly. (On the other hand, if
the errors do not accumulate randomly, the error could be of the order N.) Subtraction
between two nearly equal numbers can be disastrous. That is why use of the formula
y =
−b±
√
b
2
−4ac
2a
should be avoided if 4ac ≈ b
2
. A better choice is y
1
=−
b+sgnb
√
b
2
−4ac
2a
,
y
2
=−
2c
b+sgnb
√
b
2
−4ac
, which avoids the subtraction.
The numerical method used in approximating a given operation introduces further
errors. In the case of finite difference formulations of integral and differential calculus
280 Computational Methods—Ordinary Differential Equations
operations, as we have seen, these errors are determined by the order of approximation
made in deriving the finite difference form. It is often suggested that after performing
a procedure at one step size, the procedure should be repeated using half the original
step size. This, of course, may not be practical in large calculations, and reducing the
step size too far may increase the errors discussed in the previous paragraph.
Sometimes calculations can become unstable. An example of this would be the
solution of an ordinary differential equation where a parameter in the equation means
that there are a family of solutions generated by solving the differential equation for
various values of the parameter. If at one point in the solution space the members of the
family lie close together, round-off errors can cause the procedure to leave the original
solution and drift to a neighboring solution. A simple model of this is to compute integer
powers of the Golden Mean =
√
5−1
2
. While powers can be computed by successive
multiplications, it is easy to verify that
n+1
=
n−1
−
n
. Thus, knowing
0
= 1 and
1
=061803398, successive powers can be computed by simple subtraction.
Unfortunately, while higher powers of rapidly decrease, the function −
√
5+1
2
satisfies the same recursion relation, and this function in absolute value is greater than
unity. Unavoidable computational errors indicate that a little round-off error means
that use of the recurrence relationship will soon give completely wrong errors, usually
around the power 16 (Press et al., 1986).
Another situation where instability occurs is in dealing with stiff systems. These
systems are those where there is more than one length scale to the problem, and at least
two of the scales differ greatly in magnitude. An example is the ordinary differential
equation
d
2
y
dx
2
−100y =0. This has the general solution yx =Ae
10x
+Be
−10x
, with length
scales differing by a factor of one hundred. So, even if the boundary conditions are such
that A is zero—for example, if y0 = 1y =0—round-off errors would result in a
small nonzero value for A, and the solution would grow rapidly.
The general form of this example equation is
d
2
y
dx
2
−
2
y = 0. Here, the values of
are the eigenvalues of the problem, and the equation is stiff because in the example the
two values of differ substantially. A similar example occurs in the solution of algebraic
equations. For a set of algebraic equations Ay =b, where A is an n by n matrix and y and
b are column vectors, the eigenvalues of the matrix A are the solution of the determinant
A −I
=0, I being the identity matrix. Again, if the values of the eigenvalue differ
too greatly, the usual solution methods can run into trouble. Since finite difference
methods frequently reduce the computation to a set of algebraic equations, it should not
be surprising that stiffness can occur in both algebra and calculus.
Should the Runge-Kutta scheme not work for a particular set of equations, another
method that has been successful in some cases
2
is the Bulirsch-Stoer method, intro-
duced in 1966. The method is based on three different concepts, and so programming
it is reasonably complicated. Programs can be found in Press et al. (1986) or on the
Web. The concepts are Richardson’s deferred approach to the limit (an extrapolation
procedure), choice of a proper fitting functions (the original choice was rational poly-
nomials, but ordinary polynomials have been used), and the use of a method whose
error function is even in the step size. Further details can be found in the preceding
sources.
2
One may hope—but never expect—to find one method that works for all problems. See
www.nr.com/CiP97.pdf for some comments on this.
Problems—Chapter 11 281
Problems—Chapter 11
If available, use one of the programing languages mentioned in the book. If no such
languages are available to you, the problems can be done (if less conveniently) through
the use of spreadsheets such as Excel or Quattro Pro.
11.1 Use the trapezoidal rule to integrate the function cosx over the range 0 ≤
x ≤ 1. Perform the integration three times, using successively the intervals 0.2, 0.1,
and 0.5. Compare your computed answer with the exact result at each step of the
integration.
11.2 A technique known either as Richardson’s deferred approach to the limit or
as Richardson’s extrapolation enables improvement of the accuracy of the integration
carried out in the previous problem. For half-stepping, as was done there, if I
1
is the
result for a step size of h and I
2
, the result for a step size h/2, then the improved result
is given by I
improved
=
4I
2
−I
1
3
. Use this method to improve your results of problem 11.1.
11.3 Compare the accuracy of the finite difference approximation to the derivative
of the sine of x for the following three formulas:
Forward difference
dy
dx
yx +h −yx
h
dy
dx
−yx +2h +4yx +h −3yx
2h
Centered difference
dy
dx
yx +h −yx −h
2h
Backward difference
dy
dx
yx −yx −h
h
dy
dx
3yx −4yx −h +yx −2h
2h
Do the computation at x = /4 with h =01.
11.4 Use Euler’s method with x =01 to solve
dy
dx
=y +x y0 =0. Carry out the
integration to x = 10, and compare your result with the exact solution.
11.5 Repeat the above problem, this time using a fourth-order Runge-Kutta scheme
for integration.
11.6 The Runge-Kutta scheme of fifth-order accuracy is given by
yx +h = yx +
1
24
k
1
+
5
48
k
4
+
27
56
k
5
+
125
336
k
6
h where
k
1
=fx y
k
2
=f
x +
1
2
h y +
1
2
k
1
k
3
=f
x +
1
2
h y +
1
4
k
1
+
1
4
k
2
k
4
=fx +h y −k
2
+2k
3
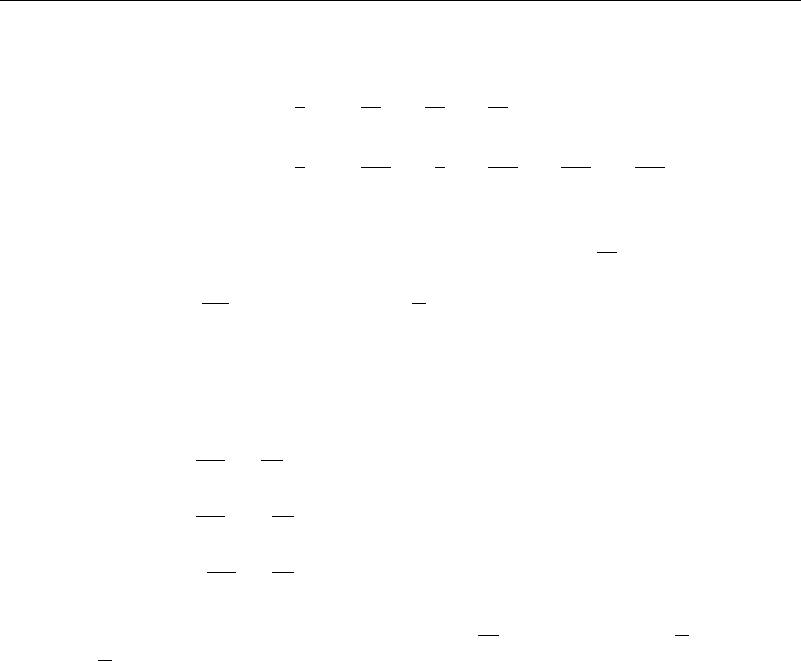
282 Computational Methods—Ordinary Differential Equations
k
5
=f
x +
2
3
h y +
7
27
k
1
+
10
27
k
2
+
1
27
k
3
k
6
=f
x +
1
5
h y +
28
625
k
1
−
1
5
k
2
+
546
625
k
3
+
54
625
k
4
−
378
625
k
5
Modify the procedure used in the previous problem and solve the same equation set.
11.7 Use the finite element method to solve the equation
d
2
y
dx
2
−
2
y = fx y0 =
y2 =0. Use the triangular elemental functions of equation (11.4.4) to find that y
j+1
−
2y
j
+y
j−1
−
h
2
2
6
y
j+1
+4y
j
+y
j−1
=
h
2
6
f
j+1
+4f
j
+f
j−1
j = 1 2 ··· N −1. The
parameter h is the constant spacing, with h = 2/N for this problem. Solve with =
1 fx = x N = 10.
11.8 Find exact solutions to the following equations, and consider how the small
parameter >0 might affect a numerical solution.
a
d
2
y
dx
2
+2
dy
dx
−y = 0y0 = 1 y = 0
b
d
2
y
dx
2
+2
dy
dx
+y = 0y0 = 1 y = 0
c
d
2
y
dx
2
+2
dy
dx
+y = 0y0 = 1 y = 0
11.9 Find the eigenvalues of the system
d
4
y
dx
4
+
4
y = 0y0 =
dy
dx
0 = y1 =
dy
dx
1 = 0 using the invariant imbedding method. This equation is associated with the
vibration of a clamped-clamped beam.
Hint: Let Z
1
= y Z
2
= y
Z
3
= y
Z
4
= y
, and let Z
1
= R
1
Z
3
+R
2
Z
4
Z
2
=
R
3
Z
3
+R
4
Z
4
. The motivation for this choice is that y and y
are known at the origin.

Chapter 12
Multidimensional Computational
Methods
12.1 Introduction 283
12.2 Relaxation Methods 284
12.3 Surface Singularities 288
12.4 One-Step Methods 297
12.4.1 Forward Time, Centered
Space—Explicit 297
12.4.2 Dufort-Frankel Method—
Explicit 298
12.4.3 Crank-Nicholson Method—
Implicit 298
12.4.4 Boundary Layer Equations—
Crank-Nicholson 299
12.4.5 Boundary Layer Equation—
Hybrid Method 303
12.4.6 Richardson Extrapolation 303
12.4.7 Further Choices for Dealing
with Nonlinearities 304
12.4.8 Upwind Differencing for
Convective Acceleration
Terms 304
12.5 Multistep, or Alternating Direction,
Methods 305
12.5.1 Alternating Direction Explicit
(ADE) Method 305
12.5.2 Alternating Direction Implicit
(ADI) Method 305
12.6 Method of Characteristics 306
12.7 Leapfrog Method—Explicit 309
12.8 Lax-Wendroff Method—Explicit 310
12.9 MacCormack’s Methods 311
12.9.1 MacCormack’s Explicit
Method 312
12.9.2 MacCormack’s Implicit
Method 312
12.10 Discrete Vortex Methods (DVM) 313
12.11 Cloud in Cell Method (CIC) 314
Problems—Chapter 12 315
12.1 Introduction
When dealing with differential equations involving more than one dimension, it is
important to know the classification of the equation, as the method of numerical com-
putation must be tied to the behavior of the equation’s solution. The three archetypical
equations are the following:
Elliptic:
2
V = 0
Parabolic:
2
V =
V
t
(12.1.1)
283
