Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.

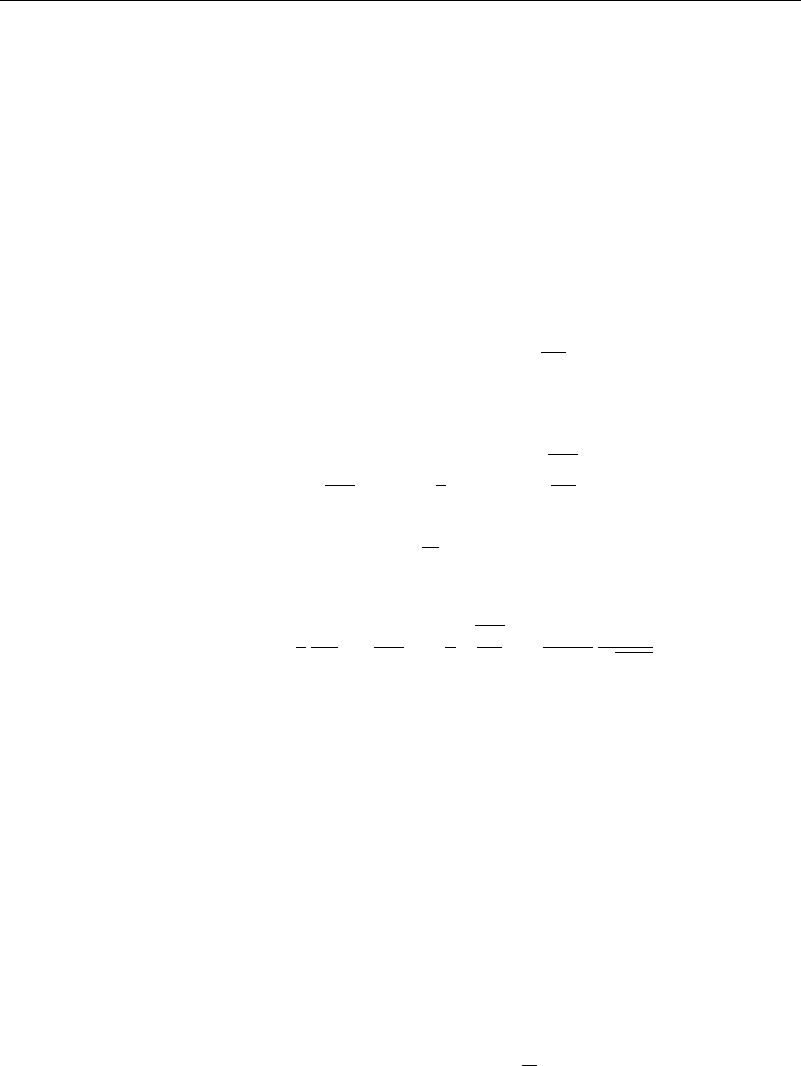
214 Low Reynolds Number Flows
The one-half in the acceleration term represents the added mass found in potential flow
theory, while the accompanying term represents a viscous correction to the added mass.
We can see that as the frequency becomes small, the result reduces to that found for the
stationary sphere.
8.5 General Translational Motion of a Sphere
The results of the previous section can be generalized to arbitrary translational motion
by use of the Fourier transform. If the velocity of the sphere is taken to be Ut, then
Fourier transform theory tells us that there is a Fourier representation of the velocity in
terms of the pair of functions
Ut =
−
Fe
−it
d and F =
1
2
−
Ute
it
dt (8.5.1)
Landau and Lifshitz (1959, page 96) showed that the drag for each harmonic component
for the previous problem is given by
a
3
e
it
6
a
2
F +
2
3
+31 +i
2
˙
F
(8.5.2)
where
˙
F is the Fourier transform of
dU
dt
. The integration of this to produce the force
requires some careful handling of the path of integration (a not uncommon problem
with Fourier integrals), the net result being
Ft =2a
3
1
3
dU
dt
+3
a
2
U +
3
a
t
−
dU
d
d
√
t −
(8.5.3)
8.6 Oseens Approximation for Slow Viscous Flow
If the solution of Section 8.2 for slow flow past a sphere were to be investigated further,
it would be found that at large distances from the sphere the neglected convective
acceleration terms were actually more important than the viscous terms retained in our
analysis. The ratio of the inertia to viscous forces is in fact of the order of Ur/.
Thus, any efforts made to try to use the Stokes approximation as a starting point for
solutions of the Navier-Stokes equations for somewhat larger values of the Reynolds
number would rapidly run into insurmountable difficulties. This has been termed the
Whitehead paradox, after the mathematician Alfred North Whitehead.
Even more embarrassing, if an attempt were made to solve the Stokes equations
for the slow flow past a circular cylinder, it would be found that the solution for the
stream function is of the form
=
Ar
3
+Br ln r +Cr +
D
r
sin (8.6.1)
The constants A and B have to be rejected because they give velocities that grow
faster with r than does a uniform stream. C represents a uniform stream, so what is
left is one constant, D, to satisfy two boundary conditions! This is known as Stokes
paradox. (A dictionary definition of paradox is “an argument that apparently derives

8.6 Oseens Approximation for Slow Viscous Flow 215
self-contradictory conclusions by valid deduction from acceptable premises.” As we
will see in the next section, in this case the “acceptable premises” were not valid.)
Oseen (1910) suggested an alternative approach, approximating the Navier-Stokes
equations by
v
t
+U
v
x
=−p +
2
v (8.6.2)
U being the free stream velocity in the x direction. Oseen obtained a solution for the
circular cylinder in terms of
v
r
=
r
+
1
2k
r
− cos
v
=
1
r
+
1
2kr
+ sin
(8.6.3)
where
=Ua
r
a
cos +A
0
ln
r
a
+
n=1
1
n
A
n
a
r
n
cosn
=Ue
kr cos
n=0
B
n
K
n
kr cos n
(8.6.4)
Here, k = U/ and the K
n
’s are the modified Bessel functions. The A
n
and B
n
are
determined from the no-slip boundary conditions.
Oseen also used his approximation to find the slow flow past a sphere. The solution
is more complicated than the Stokes equations and involves much tedious computation.
His result for the drag force is
F =6aU
1+
3
8
Re
where Re =Ua/ (8.6.5)
Stokes’s formula is seen to be the limit as Re goes to zero.
Goldstein (1929) carried out a series expansion in the Reynolds number for the
sphere using Oseen’s equations. His results for the drag coefficient gave
C
D
=
24
Re
1+
3
16
Re −
19
1280
Re
2
+
71
20480
Re
3
−
30179
34406400
Re
4
+
122519
550502400
Re
5
±···
(8.6.6)
Here the Reynolds number is based on the diameter. As we will see in the next section,
this result is not correct, since an expansion solely in powers of Re is inadequate.
The drag force per unit length of a circular cylinder as determined by the Oseen
equation was found by Lamb (1911) to be
F
per unit length
=
4U
1
2
− −log
Ua
4
(8.6.7)
where is Euler’s constant (also called Mascheroni’s constant)
= lim
n→
n
m=1
1
m
−log n
=0577215664901533 (8.6.8)

216 Low Reynolds Number Flows
Another version of the drag force on a circular cylinder was given by Tomotika
and Aoi (1950) as
C
D
=
8
ReS
1−
1
32
5
16S
−
1
2
+S
Re
2
+ORe
4
ln
2
Re
(8.6.9)
where Re =
UD
and S =
1
7
− +ln
8
Re
. Their result was achieved by using matched
asymptotic expansions.
For all of the formidable theory and numerous calculations that went into these
results, comparison with experiments (Van Dyke, 1965, page 164) seems best for the
result given in (8.6.9) up to a Reynolds number based on diameter of about 1.4.
8.7 Resolution of the Stokes/Whitehead Paradoxes
While Lamb (1932) points out many of the questions raised by the Stokes/Oseen equa-
tions, it wasn’t until the mid-1950s that the questions were finally resolved. Proudman
and Pearson (1957) and Kaplun (1957) independently pointed out that the Stokes equa-
tion hold only in the vicinity of the boundary and the Oseen equations hold only away
from the boundary. Using matched asymptotic expansions, they found that an interme-
diate region could be found where both Stokes and Oseen were valid. By matching
terms in that region, they were able to develop a solution. The result was an equation
for the drag coefficient of the sphere given by Proudman and Pearson as
C
D
=
6
Re
1+
3
8
Re +
9
40
Re
2
ln Re+ORe
2
(8.7.1)
The logarithmic term is forced by the matching process and the logarithms of the
radius that appear in both the Stokes and Oseen solutions. Any expansions involving
the Navier-Stokes equations should be aware that logarithms of the Reynolds numbers
must be anticipated. This is presaged in equation (8.6.7).
Thus, both the large Reynolds number and the small Reynolds number solutions
have a common nature. For the large Reynolds number case, Prandtl’s boundary layer
equations must be used near the boundary, and the Euler equations must be used away
from the boundary. For the small Reynolds number case, Stokes equations must be used
near the boundary, and Oseen’s equations must be used away from the boundary. This
is true for the lowest-order expansions in each category. As more than one term in the
expansion is considered, the necessary equations become modified and, as should be
anticipated, more complex.
One final remark must be made about the order of the various terms in these
expansions, particularly terms involving ln Re. As pointed out by Van Dyke (1964,
Sections 1.3, 10.5), when the next unknown term in an expansion is of order Re
n
, then
even though mathematically it is smaller than Re
n
ln Re, since it numerically can be of
equal magnitude, it should be included. That is, even though
lim
Re→0
Re
n
Re
n
ln Re
→0 for Re =001— say
Re
2
Re
2
ln Re
=
10
−4
10
−4
ln 001
=−
1
4605
=−0217
which means that for practical purposes Re
2
ln Re and Re
2
can contribute equally to a
calculation.

Problems—Chapter 8 217
Problems—Chapter 8
8.1 Show that the flow field given by v = Re
R
×e
z
p= 0 is a solution of the
Stokes equations. Use it along with a steady rotlet to find the velocity and pressure for a
fluid contained between two concentric spheres of radii a and b, where the outer sphere
is rotating with angular velocity
outer
about the x-axis and the inner sphere is rotating
with angular velocity
inner
about the same axis and in the same direction.
8.2 Millikan’s experiment for making the first accurate measurement of the charge
on an electron involved spraying a few tiny droplets of oil between two electrically
charged plates. He first determined the diameter of the small drops by measuring their
terminal velocity without an electric field V
withoutE
and using Stokes’s formula. He
then applied a voltage E (the electric potential in volts N −m/C) across the plates,
resulting in an upward force Eq/d on the drop and a terminal velocity V
withE
. Here, d
is the plate spacing in meters, and q is the electron charge in Coulombs (C). Making
repeated measurements, he found that the values of q he determined were always integer
multiples of a specific number q
1
, the charge due to a single electron. Determine first a
formula for the droplet diameter when no electric field is present. Then determine the
terminal velocity when the electric field is present. Solve for q in terms of the weight
of the droplet minus the buoyancy force, the terminal velocities with and without an
electric field, and the quantity E/d.
8.3 In a repeat of Millikan’s experiment (Problem 8.2), the voltage was 115 volts,
the plate spacing 4.53 mm, the oil density was 920 kg/m
3
, and the air viscosity was
182 ×10
−4
poise. Two horizontal lines were drawn 1.73 mm apart, and the time of
traverse of these two lines was measured with a stopwatch. By changing the direction
of the electric filed, it was possible to use the same droplet for each measurement,
although each set of measurements did have different numbers of electrons attached to
the droplet. Times of transit were as follows:
72.2 seconds averaged over 10 measurements, no electric field, direction down
41.1 seconds averaged over 8 measurements, electric field present, direction up
23.5 seconds averaged over 2 measurements, electric field present, direction up
16.5 seconds averaged over 5 measurements, electric field present, direction up
12.5 seconds averaged over 3 measurements, electric field present, direction up
8.06 seconds averaged over 7 measurements, electric field present, direction up
Find the terminal velocities for the six sets of data, and estimate the charge due to a
single electron. Be sure to observe the proper sign on the velocities.
Note: Millikan also found that Brownian motion due to the small size of these
droplets gives errors in measuring velocity, resulting in charge estimates that are about
27% too high.

Chapter 9
Flow Stability
9.1 Linear Stability Theory of Fluid
Flows 218
9.2 Thermal Instability in a Viscous
Fluid—Rayleigh-Bénard
Convection 219
9.3 Stability of Flow Between Rotating
Circular Cylinders—Couette-Taylor
Instability 226
9.4 Stability of Plane Flows 228
Problems—Chapter 9 231
9.1 Linear Stability Theory of Fluid Flows
Chapters 3 and 4 examined several examples that involved the stability of inviscid
flows, such as the round jet, the vortex street, and several cases of interfacial waves. In
those cases an infinitesimal disturbance was added to a primary flow, and then it was
determined whether there was a possibility of the disturbance growing, decaying, or
remaining unchanged. The driving mechanisms involved in those examples were gravity
and surface tension interacting with the momentum of the flow.
In this chapter the same type of analysis is used and applied to laminar viscous
flows as well. The presence of viscosity in some cases will dampen the destabilizing
influences and in others act to enhance them and thus destabilize the primary flow. Flows
frequently are laminar for sufficiently small values of a dimensionless parameter, such
as the Reynolds number, and become turbulent once the parameter becomes sufficiently
large. While this transition value of the parameter can be found experimentally, as
Reynolds did for pipe flow, in many cases a flow has so many describing parameters
that a complete experimental study becomes too costly. An analytic approach then can
be desirable, with the added advantage of possibly shedding some light on the physical
mechanisms involved in the transition.
The classical approach in studying such transitions, introduced in the nineteenth
century in the study of inviscid flows, is to take the solution for the laminar flow and
add to it a very small disturbance. There is usually some experimental knowledge of
the form of the instability, and the disturbance is tailored to reflect this. This combined
flow is then put into the Navier-Stokes equations, and the original laminar flow terms
are subtracted. By themselves, the primary flow satisfies the Navier-Stokes equations.
218

9.2 Thermal Instability in a Viscous Fluid—Rayleigh-Bénard Convection 219
However, some interaction terms between the primary and secondary flows remain
behind by this process. The remaining equations are then linearized in the disturbance
quantities. This set of partial differential equations is then solved to determine whether
the disturbance will grow or decay in time. For viscous flows, the mathematics for
finding the solution of the stability equations is generally much more complicated than
it is for inviscid flows, due to the higher order of the resulting differential equations
and also possible additional physical mechanisms for supporting the instability.
The use of infinitesimal disturbances results in linear equations, which by them-
selves have proven difficult to solve. In some of the cases where nonlinear formulations
have been made and solutions found, the efforts naturally increase the difficulty of
finding a solution. Landau and Lifshitz (1964) present some of the procedures and
assumptions involved with these nonlinear equations.
Because a linear approach is being used, if our solution predicts an unstable solution
of the primary flow, this by itself cannot predict the nature of the secondary flow. In
some cases a direct transition to turbulent flow exists, and in others, secondary laminar
flows evolve, more complicated in nature than the original primary flow but still not the
fully complex character associated with turbulent flow. Some flows also can evolve to
have tertiary flows that are still laminar. Such is the complexity of fluid flow behavior!
9.2 Thermal Instability in a Viscous Fluid—
Rayleigh-Bénard Convection
One of the least mathematically complicated examples of the analysis of viscous flow
instability is due to Lord Rayleigh (1916a). Several investigators in the nineteenth
century had noted that tesselated structures were frequently seen in the drying of
horizontal thin layers of fluids. Bénard (1900, 1901) performed quantitative experiments
on this phenomenon, most of the details later explained by Rayleigh’s analysis. This
instability can be seen in the drying of paints with metallic particles and also in the
stratified atmosphere, where it results in interesting cloud patterns.
While there are many versions of the boundary conditions that can be studied,
only the case of a fluid confined between two horizontal plates, each with horizontal
extent large compared to their vertical spacing, will be considered here. (A thorough
description of the extensive literature available on this problem is given in Koschmeider
(1993)). The plates are each heated to a constant temperature, with the lower plate being
the hottest, as shown in Figure 9.2.1. Thus, there is a basic gravitational instability,
with lighter fluid on the bottom. Initially, the fluid between the plates is at rest, with a
z
T
hot
T
cold
d /2
d
/2
Figure 9.2.1 Physical layout for studying Bénard stability

220 Flow Stability
vertical hydrostatic pressure gradient. The density will be taken as varying linearly with
temperature according to
=
mean
1−T −T
mean
with T
mean
=
T
hot
+T
cold
2
(9.2.1)
Here, reference density
mean
and reference temperature T
mean
have been taken as the
density and temperature midway between the plates. Beta is given by
=−
1
d
dT
=−
1
d
dz
dz
dT
=−
1
T
(9.2.2)
The plate spacing will be chosen as b, and the origin will be taken halfway between the
plates.
Since there is no mean flow for this problem, the Navier-Stokes and energy equa-
tions for the primary undisturbed flow are given by
T
0
=T
mean
−
z
b
T
0
=
mean
1−
z
b
T
with T = T
hot
−T
cold
(9.2.3)
Here, primary flow components p
0
z
0
, and T
0
z are denoted by the subscript 0,
and k is a unit vector in the direction of gravity z. From these and the boundary
conditions, and taking the origin halfway between the plates, find for the quiescent
primary flow that
0 =−p
0
−gk
0
(9.2.4a)
0 = k
d
2
T
0
dy
2
(9.2.4b)
To investigate the stability of this flow, introduce a small disturbance and see
whether it grows or decays. For the disturbed flow, velocities, pressure, density and
temperatures will be denoted by primes. The combined primary and disturbance flows
must satisfy the continuity, Navier-Stokes, and energy equations.
It shall be assumed that even though the basic density does vary with z, the main
influence of the density variation on the flow stability is going to be felt in the body
force and not in the acceleration term. Thus, the
0
multiplying the acceleration term
is taken at its mean value and is considered constant, and the flow will be regarded as
being incompressible. This is called the Boussinesq approximation.
After linearizing on the small disturbance terms and then subtracting out the primary
flow terms, the terms’ first order in the primed quantities are
mean
·v
=0 (9.2.5)
mean
v
t
=−p
+
mean
gT
k +
2
v
(9.2.6)
mean
c
p
T
t
−v
z
T
b
=k
2
T
(9.2.7)
Together with the conditions that v
and T
vanish at each plate, the mathematical
statement of the problem has been completed. Now these equations must be made
manageable.
The first step is to eliminate the pressure. Taking the divergence of equation (9.2.6)
and using the continuity condition equation (9.2.5) gives
0 =−
2
p
+
mean
g
T
z
(9.2.8)

9.2 Thermal Instability in a Viscous Fluid—Rayleigh-Bénard Convection 221
Similarly, operating on the z component of equation (9.2.6) with the Laplace operator
gives
mean
t
2
v
z
=−
z
2
p
+
mean
g
2
T
+
2
2
v
z
(9.2.9)
Using equation (9.2.8) to eliminate the pressure in equation (9.2.9) gives
mean
t
2
v
z
=−
z
mean
g
T
z
+
mean
g
2
T
+
2
2
v
z
which simplifies to
mean
t
−
2
2
v
z
=
mean
g
2
1
T
where
2
1
=
2
−
2
z
2
=
2
x
2
+
2
y
2
(9.2.10)
Next, rewrite equation (9.2.7) in the form
mean
c
p
t
−k
2
T
=
mean
c
p
T
b
v
z
(9.2.11)
Equations (9.2.10) and (9.2.11), then, are two equations in the two unknowns v
z
and T
.
Since the plates are considered to be large in extent, no boundary conditions will
be imposed at the edges of the plates. The boundary conditions imposed are simply
v
x
=v
y
=v
z
=T
=0onz =±
b
2
At this point the velocity components and the temperature can be taken as being of
the form
v
x y z t = Uz Vz Wzfx ye
st
(9.2.12)
T
x y z t = zfx ye
st
(9.2.13)
where
2
f
x
2
+
2
f
y
2
=−
a
2
b
2
f (9.2.14)
This form allows separation of variables and is sufficiently general to describe the
observed flows.
If you have studied separation of variables in a mathematics course, you many
be surprised that this separable form had to be assumed rather than have it follow
from the analysis. The reason is that classical presentations of the method of separation
of variables all deal with second-order partial differential equations, while here our
system is actually of sixth order. Generally, systems of order higher than the second
do not separate except under very special boundary conditions. The governing equation
introduced for f allows for separating the variables and is compatible with a number of
boundary conditions. Further comments on the nature of f will be made a bit later.
Putting these forms into our system of equations, using equation (9.2.9) and can-
celling f where it appears in every term of the equation, equations (9.2.5), (9.2.10), and
(9.2.11) become
U
f
x
+V
f
y
+f
dW
dz
=0 (9.2.15)

222 Flow Stability
mean
s −
d
2
dz
2
−
a
2
b
2
d
2
dz
2
−
a
2
b
2
W =−
a
2
b
2
mean
g (9.2.16)
mean
c
p
s −k
d
2
dz
2
−
a
2
b
2
=
T
b
W (9.2.17)
Note from equation (9.2.15) that U = V = 0 on the boundaries implies that
dW
dz
=0on
the boundaries also.
It is possible that the time constant s could be complex. The real portion would be
associated with a growth or decay rate, and the imaginary part with an oscillatory behavior.
To show that the oscillatory behavior cannot occur, perform the following operations:
1. The momentum equation (9.2.16) is multiplied by the complex conjugate of W ,
denoted as W
∗
, and integrated over the gap between the plates. Using integration by
parts and the boundary conditions then gives
s
mean
b
2
J
1
+
b
4
J
2
=−
mean
g
a
2
b
2
b/2
−b/2
W
∗
dz (9.2.18)
where
J
1
=b
2
b/2
−b/2
dW
dz
2
+
a
2
b
2
W
2
dz
J
2
=b
4
b/2
−b/2
d
2
W
dz
2
2
+2
a
2
b
2
dW
dz
2
+
a
4
b
4
W
2
dz
are both positive definite.
2. The energy equation (9.2.17) is multiplied by the complex conjugate of , denoted
as
∗
, and integrated over the gap between the plates. Using integration by parts and
the boundary conditions gives
mean
bc
p
T
k
2
s
mean
c
p
I
0
+
k
b
2
I
1
=−
mean
c
p
T
b
b/2
−b/2
W
∗
dz
where I
0
=
k
mean
bc
p
T
2
1
C
2
b/2
−b/2
2
dz
I
1
=
bk
mean
bc
p
T
2
b/2
−b/2
d
dz
2
+
a
2
b
2
2
dz
(9.2.19)
are both positive definite. The rather awkward-appearing combination of parameters
appearing before the Is are to make the dimensions coincide in the final result.
Notice that, except for multiplying constants, the right-hand sides of equations
(9.2.18) and (9.2.19) are the complex conjugates of one another. From this it follows that
s
mean
c
p
b
2
k
1
Pr
J
1
+J
2
=a
2
Ra
s
∗
mean
c
p
b
2
k
I
0
+I
1
(9.2.20)
where Pr is the Prandtl number and Ra =
b
3
g
2
mean
c
p
T
k
is called the Rayleigh number.
Taking the imaginary portion of both sides of equation (9.2.20) gives
s
i
J
1
=−s
i
PrRaI
0
giving s
i
J
1
+PrRaI
0
=0 (9.2.21)

9.2 Thermal Instability in a Viscous Fluid—Rayleigh-Bénard Convection 223
It follows from this that if Ra is positive (Ra is positive if T is positive, so heavier
fluid is on the bottom), s must be real.
If the real portion of both sides of equation (9.2.20) is taken, the result is
s
r
mean
c
p
b
2
k
1
Pr
J
1
−a
2
RaI
0
=a
2
RaI
1
−J
2
(9.2.22)
This states that the real part of s can be either positive or negative if T is positive.
The results of the previous paragraph are often referred to as the principle of
exchange of stabilities. While the appropriateness of this title is unclear, the usefulness
of the principle is without doubt.
Since equations (9.2.16) and (9.2.17) have constant coefficients, their solution is in
the form of exponentials and they can be found in a standard manner. That is, letting
W =Ae
cz/b
=Be
cz/b
, equations (9.2.16) and (9.2.17) become
mean
sb
2
−
c
2
−a
2
c
2
−a
2
A =−a
2
b
2
mean
gB
mean
c
p
b
2
s −k
c
2
−a
2
B =
mean
c
p
bTA
Eliminating A and B between these two equations, find that c must satisfy
c
2
−a
2
c
2
−a
2
−
mean
c
p
b
2
k
s
c
2
−a
2
−
mean
s
+a
2
Ra =0 (9.2.23)
where Ra is the Rayleigh number as just defined.
Equation (9.2.23) is a cubic equation for c
2
, whose solution is somewhat messy.
The calculations can be simplified by saying that only the neutrally stable case is desired
to be solved; that is, only the results where the real part of s vanishes will be studied.
In that case the roots become
c
2
n
=a
2
1−
Ra
a
1/3
cos
2n
3
+i sin
2n
3
n= 0 1 2 (9.2.24)
The solution can now be expressed in terms of these roots. Since they occur in
complex conjugate pairs, write
W =
2
n=0
A
n
cosh
c
n
z
b
+B
n
sinh
c
n
z
b
=
−
ga
2
b
2
2
n=0
c
2
n
−a
2
2
A
n
cosh
c
n
z
b
+B
n
sinh
c
n
z
b
Require that U V W , and vanish on z =±b/2, or equivalently, from continuity
require that W, dW/dz, and vanish at these boundaries. The result is
