Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


234 Turbulent Flows
to increase lift on airplane wings or decrease drag on autos, ships, and planes, keeping
things laminar as long as possible may be better.
Thus, it is necessary to understand the rudiments of turbulence, both from theory
and experiments, and to find ways to predict what turbulence does to fluid flow. This
will not be as clear-cut as in the case of laminar flow, but some information can be
obtained.
Several approaches have been used to develop equations suited for the study of
turbulent flow. Since the Navier-Stokes equations are valid for both laminar and turbulent
flows, they usually serve as a general starting point. The complexity and rich detail
of what transpires in turbulent flow, however, limits our abilities to fully tackle the
Navier-Stokes equations directly. This is because the major effect of turbulence is that of
mixing. As the Reynolds number increases, the range of the length scales of the various
eddies in the flow also increases. Such a range of detail in the flow cannot be dealt
with entirely by analytic means, and it poses a challenge to the largest supercomputers
available. Computer simulations of the full Navier-Stokes equations are usually limited
to flows where periodicity of the flow can be assumed and the boundaries are of
particularly simple shape, usually rectangular. Numerical grids used must be small
enough to resolve the smallest significant eddy scale
1
present in the flow, and the
simulation must be carried out for a sufficiently long time that initial conditions have
died out and significant features of the flow have evolved. The necessary memory and
speed requirements on computers has in fact been one of the principle driving factors
in the evolution of supercomputers and distributed computing architecture.
Covering the complete spectrum of eddy length scales is necessary, since different
physical mechanisms are important at various places in the spectrum. Large-scale eddies
contain much of the kinetic energy and little of the vorticity. The eddies tend to be
anisotropic (i.e., the turbulence behaves differently in different spatial directions), and
viscous effects are not important. These large eddies gradually break down into smaller
eddies that have little kinetic energy but much vorticity. The small eddies tend to be
isotropic, and viscous effects are important for them because it is the mechanism for
converting the kinetic energy of the turbulence finally into heat.
10.2 Statistical Approach—One-Point Averaging
The vast amount of detail in turbulent flows requires that many features be looked at in
a statistical sense. That is, for any turbulent quantity (e.g., velocity or pressure), split
the flow into a time mean quantity and a turbulent fluctuation quantity. For example,
letting unmarked quantities denote the total value, superposed bars denote an average,
and primes denote the turbulent portion, for velocity, temperature, and pressure, write
v =
v +v
(10.2.1)
p =
p +p
(10.2.2)
where the average of a quantity (pressure for example) is given by
p =
1
0
pdt (10.2.3)
1
An eddy is defined as an entity that contains vorticity. See Lighthill, in Rosenhead (1963), Introduction.
Boundary Layer Theory, Chapter II.

10.2 Statistical Approach—One-Point Averaging 235
This is also called the first moment of the pressure. The averaging time is a time scale
sufficiently long compared to the fluctuation times present in the flow. Notice that for
any fluctuating quantity, it follows by definition that
p
=0 (10.2.4)
The root mean square value (designated by rms, and also called the second moment)
gives some idea as to the size of a fluctuation quantity. It is defined in the case of
pressure, for example, by
rms p =
p
p
=
1
T
T
0
p
p
dt (10.2.5)
This term is never zero unless pressure fluctuations are completely absent from the
flow. This second-order moment is a correlation of p
with itself and is thus called an
autocorrelation.
Reynolds first looked at the Navier-Stokes equations in this manner and introduced
what are now called the Reynolds averaged Navier-Stokes equations. To see how the
equations are found, start first with the continuity equation for a constant density flow.
2
Splitting the velocity as in equation (10.2.1) results in
·v = ·
v+ ·v
=0 (10.2.6)
Averaging equation (10.2.6) and using the fact that the average of a fluctuation is zero,
this reduces to
·
v = 0 (10.2.7)
Substituting this into equation (10.2.6) gives also
·v
=0 (10.2.8)
Consider next the component of the Navier-Stokes equations in the x
i
direction.
It is convenient to use index notation for much of what follows, so we will alternate
between using v = uvw and v = v
1
v
2
v
3
in what follows. It is also convenient to
write the Navier-Stokes equation in the index notation form (with the help of continuity
equation (10.2.6)):
v
i
t
+
v
i
v
j
x
j
=−
p
x
i
+
x
j
v
i
x
j
+
v
j
x
i
(10.2.9)
The summation convention on repeated subscripts is being used here—that is,
v
i
v
j
x
j
=
3
j =1
v
i
v
j
x
j
=
v
i
v
1
x
1
+
v
i
v
2
x
2
+
v
i
v
3
x
3
i=1 2or3
2
In this presentation, to avoid a large degree of additional complication temperature and fluid properties
such as density and viscosity will be assumed to be constant. Variations in these quantities can be included
in a similar fashion with substantial additional effort.

236 Turbulent Flows
Decomposing the velocities into mean and turbulent parts, inserting these into
equation (10.2.9) and then averaging, results in
v
i
t
+
v
i
v
j
x
j
+
v
i
v
j
x
j
=−
p
x
i
+
2
v
i
x
2
j
(10.2.10)
or upon rearranging,
v
i
t
+
v
i
v
j
x
j
=−
p
x
i
+
x
j
v
i
x
j
−v
i
v
j
(10.2.11)
The terms in equation (10.2.11) that involve averages of the products of the turbulent
fluctuations
−
v
2
1
−v
2
2
−v
2
3
−v
1
v
2
−v
1
v
3
−v
2
v
3
or
−
u
2
−v
2
−w
2
−u
v
−u
w
−v
w
(10.2.12)
are called the Reynolds stresses. They are the terms through which the turbulence
fluctuations interact with and change the mean flow. At a solid boundary they must
vanish, but usually they have large gradients near a boundary and reach maximum
values very close to the wall. They can be measured by means of hot wire anemometers
or laser doppler anemometry, with suitable processing of the signals. They represent
what are called second-order correlations of the velocity at a given point.
Notice that in the averaging process, we have gone from a fully determinate system,
one where the number of unknowns is equal to the number of equations, to one that is
indeterminate, in that we now have more unknowns than equations. To attempt to correct
this, we could first multiply the Navier-Stokes equations by some quantity such as a
velocity component, then average the equations so obtained. In the process we would
introduce averages of three velocity fluctuation components (third-order correlations)
and find that the system is even more indeterminate than before. This game is one
that can’t be won, as this statistical averaging process will continue to generate new
unknowns faster than it generates new equations. As the order of a correlation increases,
the difficulties of both accurate measurement and physical understanding decrease,
and seldom is it necessary or useful to go beyond fourth-order correlations—if indeed
that far!
It should be noticed that although the statistical approach has many advantages
and is one of the few well-developed mathematical procedures available for analyzing
turbulent flows, it also has disadvantages. Averaging hides rather than reveals the
underlying physical processes that take place in such flows. Mollo-Christiansen (1971)
has given the example of a blind person using a single sensor on a single road as an
attempt to discover what kinds of vehicles used that road. “Happening to use a road
traveled only by limousines and motorcycles, he concluded that the average vehicle is
a compact car with 2.4 wheels.”
3
At first it may seem strange that although the Navier-Stokes equations are closed
mathematically, the statistical equations obtained from them are not. Batchelor (1971)
has given two complementary answers to this. He notes that the Navier-Stokes equations
3
The remark was made to point out the inadequacy of using a single sensor.
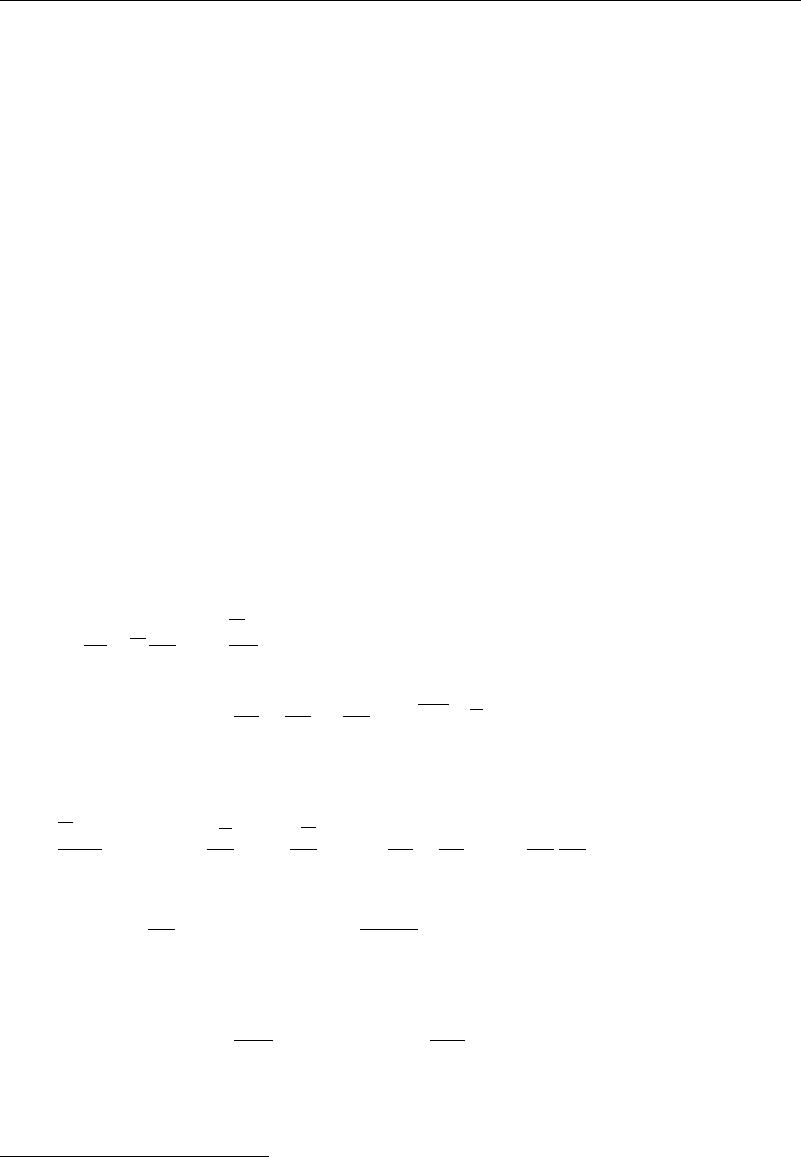
10.2 Statistical Approach—One-Point Averaging 237
are open in time, since any one flow realization must be integrated over the whole
of future time before exact values can be found for the various correlations. This is
contrasted with the equations for the correlations, which can be made independent of
time. Second, additional correlations give less and less additional information so that
only a finite number of correlations is required to determine the properties of a turbulent
field to sufficient accuracy.
The problem of finding a way to get the same number of unknowns as equations is
called the closure problem of turbulence. In the elementary fluids course you may have
taken, you might have seen algebraic attempts at closure such as mixing length and eddy
viscosity. There, the Reynolds stresses were approximated in terms of mean quantities
and their gradients. While these closure models are useful for providing a correlation of
experimental data in simple flows such as pipe flow, they often fail when they are applied
to situations outside of the range of the original experiments. They have nevertheless
been developed to a high degree of complexity (see, for instance, Section 5.2.3 of
Bradshaw (1978)) and can give good results for boundary layer–type flows.
Before going to a discussion of closure formulas, three more correlation
equations will be developed. These are the transport equations for the important
correlations—namely, Reynolds stresses, kinetic energy, and dissipation. Deriving the
equations is an involved process, and it is necessary to use index notation because of the
nature of the terms involved in the needed multiplications. Also, it eases the physical
interpretation of the various terms.
Derivation of the first correlation equation starts with equation (10.2.9) with the
velocity written in decomposed form. This is next subtracted from equation (10.2.11),
giving
v
i
t
+
v
k
v
i
x
k
≡
Dv
i
Dt
=−
p
x
i
+
x
k
v
i
x
k
−
v
i
v
k
+v
i
v
k
+v
i
v
k
(10.2.13)
Multiplying equation (10.2.13) by v
j
and adding to this the same quantity but with the
i and j interchanged,
4
we get
Dv
i
v
j
Dt
=−
v
j
v
k
v
i
x
k
+v
i
v
k
v
j
x
k
+p
v
j
x
i
+
v
i
x
j
−2
v
i
x
k
v
j
x
k
−
x
k
p
v
j
ik
+v
i
jk
−
v
i
v
j
x
k
+v
i
v
j
v
k
(10.2.14)
Time averaging equation (10.2.14) then gives
DR
ij
Dt
=P
ij
+T
ij
−D
ij
−
J
ijk
x
k
I II III IV V
(10.2.15)
4
For example, for an equation a
i
= b
i
, multiplication gives v
j
a
i
= v
j
b
i
, so after the interchange and
addition, we have v
j
a
i
+v
i
a
j
=v
j
b
i
+v
i
b
j
.

238 Turbulent Flows
where
D
ij
=2
v
i
x
k
v
j
x
k
=dissipation of Reynolds stress,
J
ijk
=
1
p
v
j
ik
+p
v
i
jk
−
R
ij
x
k
+
v
i
v
j
v
k
=flux of Reynolds stress,
P
ij
=−
R
ik
v
k
x
j
+R
jk
v
k
x
i
=production of Reynolds stress,
R
ij
=v
i
v
j
=−Reynolds stress/
T
ij
=
1
p
v
i
x
j
+
v
j
x
i
=pressure strain rate.
The roman numerals under the various terms indicate the source of that term and
the role it plays in affecting the turbulence. The physical interpretation of the terms are
as follows:
•
Transport of the correlation—in this case, the Reynolds stresses. This term
represents convection of the correlation with the mean velocity.
•
Generation or production. The presence of mean velocity and temperature gra-
dients allows energy to be transferred between the mean and fluctuating field.
The energy can in principal flow either way—that is, from the mean flow into
the turbulence or vice versa. The first is generally more prevailing. These terms
arise from the fluctuating portion of the convective term.
•
Redistribution (also called pressure-strain). In an incompressible flow the inter-
actions of the pressure fluctuations can neither create nor destroy energy. Rather,
they cause it to be redistributed among the various components of the correlation.
•
Destruction. This term comes from the viscous stresses and results in a decrease
of the correlation expressed in transport of the correlation.
•
Diffusion. These terms arise from the fluctuating convection, pressure, and viscous
terms. They are characterized by being expressible as the gradient of a tensor.
For the second correlation equation, the disturbance velocity vector is dotted with
the Navier-Stokes equations and then time averaged. The result can be obtained from
the previous result by contracting on i and j, giving
Dk
Dt
=P−D−
J
∗
k
x
k
IIIIVV
(10.2.16a)
where
D =
1
2
D
ii
=
v
i
x
k
v
i
x
k
=homogeneous dissipation of Reynolds stress,
J
∗
k
=
1
2
J
iik
=
1
p
v
k
+
1
2
v
i
v
i
v
k
−
k
x
k
=flux of Reynolds stress,
J
k
=
1
p
v
k
+
1
2
v
i
v
i
v
k
−2
v
i
v
i
x
k
+
v
k
x
i
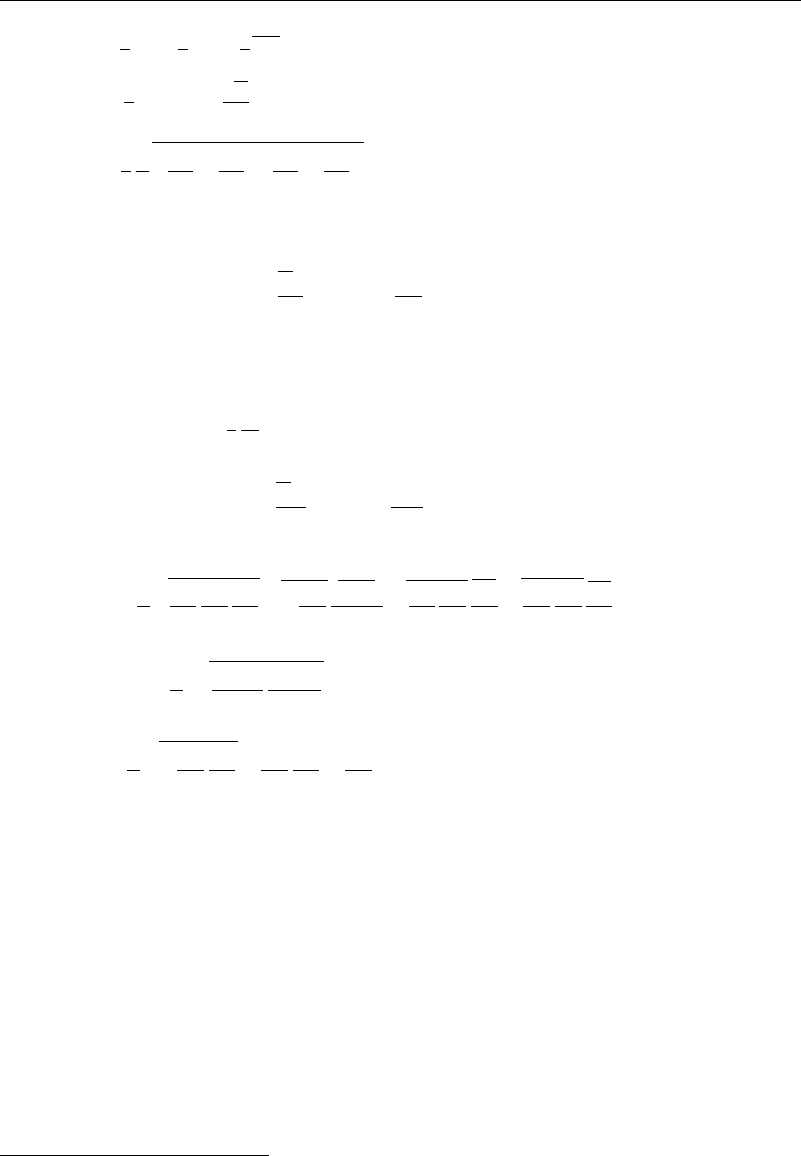
10.2 Statistical Approach—One-Point Averaging 239
k =
1
2
q
2
=
1
2
R
ii
=
1
2
v
i
v
i
=turbulent kinetic energy,
P =
1
2
P
ii
=−R
ij
v
i
x
j
=rate of kinetic energy production,
=
1
2
v
i
x
j
+
v
j
x
i
v
i
x
j
+
v
j
x
i
=total rate of energy dissipation.
This equation is also found in the literature written in the alternate form
Dk
Dt
=P−−
J
k
x
k
IIIIVV
(10.2.16b)
The Roman numerals under the various terms are interpreted as for equation (10.2.16).
The third equation is found by first differentiating the Navier-Stokes equations
and then multiplying it by
v
i
x
j
, adding the interchanged equation, and averaging the
result. This gives
DD
Dt
=−W −
H
k
x
k
(10.2.17)
where
W =2
v
i
x
j
v
j
x
k
v
k
x
i
+v
j
v
i
x
k
2
v
m
x
j
x
k
+
v
i
x
j
v
i
x
k
v
j
x
k
+
v
i
x
k
v
j
x
k
v
i
x
j
+2
2
2
v
i
x
j
x
j
2
v
i
x
k
x
k
(10.2.18)
H
j
=
v
j
v
i
x
k
v
j
x
k
+
v
j
x
k
p
x
k
−
D
x
k
The various correlations introduced so far are called one-point correlations. This
means that every velocity and/or pressure term in the correlation is measured at the same
point. At times two-point correlations are also used in turbulence studies, when one is
trying to ascertain how what happens at a downstream point is affected by what happens
at an upstream point.
5
Similar correlation transport equations can be developed for such
correlations, but, of course, even more algebra is involved. Two-point correlations have
been used in turbulence calculations but to a much more limited extent than one-point
correlations.
At least five different approaches have been used to provide closure formulae for
our equations:
1. Zero-equation models. This approach uses equation (10.2.11) as the only
partial differential equation. The Reynolds stresses are modeled by algebraic
5
One example of such a correlation could be the degree to which the proverbial butterfly flapping his
wings in Beijing affects the climate in your location.

240 Turbulent Flows
expressions, based largely on eddy viscosity and mixing length concepts,
and equation (10.2.11) is used to determine mean flow. This is widely used
in practical applications, and it also crops up in the one- and two-equation
models.
2. One-equation models. Another partial differential equation involving a tur-
bulence velocity scale is used along with equation (10.2.11), often equation
(10.2.16). The length scale often used is based on q or .
3. Two-equation models. Two partial differential equations involving two turbu-
lence velocity scales are used along with equation (10.2.11), usually equations
(10.2.16) and (10.2.17). Length scales often are based on q and .
4. Stress-equation models. Partial differential equations are used for all Reynolds
stress components and often for a length scale as well.
5. Large eddy simulations. Computations are made for both large-scale and small-
scale eddies.
In the following sections these methods will be discussed in more detail. A number
of reviews are available in the literature and should be consulted for more information.
Among them are Bradshaw (1972), Mellor and Herring (1973), Reynolds (1974, 1976),
Reynolds in Bradshaw (1978), and Bradshaw, Cebeci, and Whitelaw (1981).
Much of the early work in theoretical turbulence models was done for special
models: homogeneous turbulence, where the turbulence is the same in every location
(e.g., Batchelor 1967); isotropic turbulence, where at a given point the turbulence is
both homogeneous and independent of direction (e.g., Taylor, 1935–1938); and turbulent
shear flows (e.g., Townsend 1956).
6
While the concepts seem simple in hindsight, the
results together with Taylor’s experiments demonstrated the power of the statistical
approach (Kármán 1937b, 1938; Komogoroff 1941; Batchelor 1947).
10.3 Zero-Equation Turbulent Models
The eddy viscosity
T
and mixing length formulas
−
u
v
=
2
d
u
dy
d
u
dy
and −
u
v
=
T
du
dy
(10.3.1)
form the basis for most of these models. Many variations on them exist. For instance,
at large Reynolds numbers Re > 5000, it is common to neglect the viscous sublayer
and split the boundary layer region into two parts. An example of this is
=
04y y
0
≤y ≤y
c
0075 y
c
≤y ≤
T
=
⎧
⎪
⎨
⎪
⎩
2
d
u
dy
y
0
≤y ≤y
c
00168
x
0
u
c
−u
dy
y
c
≤y ≤
(10.3.2)
6
It should be noted that although Reynolds introduced the concept of what are now called Reynolds
stresses, the concept of statistical analysis of turbulent flows languished until Taylor in 1935 revived the idea
and brought it to the attention of researchers.

10.3 Zero-Equation Turbulent Models 241
Here, y
0
= 40/u
c
is the thickness of the viscous sublayer measured from the
wall, and y
c
is another distance found from making the mixing length continuous. The
parameter is a boundary layer thickness, defined, for example, where the mean velocity
is at 0.5% of the outer flow.
A number of empirical corrections of these formulae have become feasible over
the years as computing memory and speed have increased. One due to Cebeci and
Smith (1967, 1974) gives improved results for low Reynolds numbers, transition, mass
transfer, pressure gradients, and boundary curvature. The eddy viscosity is given by
T
=
T
i
T
o
=
⎧
⎪
⎨
⎪
⎩
2
d
u
dy
y≤y
crossover
00168
x
0
u
c
−u
dy
F
Klebanoff
y>y
crossover
(10.3.3)
The quantity y
crossover
is where the outer eddy viscosity is greater than the inner viscosity.
The other quantities are
=04y
1−e
−y
+
/A
+
A
+
=26
1+
y
wall
dp
dx
−1/2
(10.3.4)
F
Klebanoff
=
1+55
y
6
−1
F
Klebanoff
being a factor introduced by Klebanoff to account for intermittancy in the flow.
The quantity y
+
is given by y
+
=u
∗
y/, where u
∗
=
wall
/. The expression for the
mixing length is the van Driest fit to velocity measurements near the wall. This model
was extended to three dimensions and also accounts for compressibility effects. It was
developed by Cebeci (1974), Cebeci and Abbott (1975), and Cebeci et al. (1975).
Because of its robustness, a model by Baldwin and Lomax (1978) is commonly
used in quick design iterations. It does not capture all details of the turbulence but still
gives useful design information. Its details are given by
T
=
⎧
⎨
⎩
T
i
T
0
=
⎧
⎨
⎩
2
y≤y
crossover
KC
cp
F
wake
F
Klebanoff
y>y
crossover
(10.3.5)
The y
+
is as given in equation (10.3.4). Other quantities are
ij
=
1
2
u
i
x
j
+
u
j
x
i
=
ij
ij
=
1−e
−y
+
/A
+
F
wake
=min
y
max
F
max
C
wk
y
max
u
dif
2
/F
max
y
max
and F
max
are the maximum of the function Fy =y
1−e
−y
+
/A
+
,
F
Klebanoff
=
1+55
yC
Klebanoff
y
max
6
−1
u
dif
=max
u
i
u
i
−min
u
i
u
i

242 Turbulent Flows
The various constants are given by
A
+
C
cp
C
Klebanoff
C
wk
26 1.6 0.3 0.25 0.4 0.0168
Granville (1987) has suggested improvements in these constants. Further comments
have been made by Wilcox (1998).
10.4 One-Equation Turbulent Models
An early model due to Prandtl (1945) suggested that
T
=
√
k (10.4.1)
with k being the turbulent kinetic energy and the mixing length coming from an algebraic
formula. The turbulent kinetic energy is usually determined from equation (10.2.16b)
after suitable modeling of the terms on the right-hand side. A model used at Stanford
University in the STAN-5 code let
T
=c
2
q
R
ij
=
1
3
q
2
ij
−
T
u
i
x
j
+
u
j
x
i
D = c
3
q
2
/
J
∗
j
=−
c
4
T
+
q
2
x
j
(10.4.2)
where the length scale is modeled by means described in the zero-equation model.
Typically the zero-equation model is used for y
+
≤2A
+
, and the preceding is used for
greater values of y
+
. STAN-5 uses c
2
=038c
3
=0055c
4
=059, all determined from
experimental results. A similar model was developed at Imperial College (Wolfshtein,
1969). Further forms for one-equation models can be found in the review by Mellor and
Herring (1973).
10.5 Two-Equation Turbulent Models
The previous models required specification of a turbulent-length scale for their realiza-
tion. To avoid this, equation (10.2.17) is frequently used to compute the dissipation. For
the case of isotropic turbulence,
D =−
1
2
q
2
and
DD
Dt
=−W (10.5.1)
For large values of the Reynolds number, after making the assumption that W is of the
form W =c
7
D
2
/q
2
, the solution of equation (10.5.1) is
q
2
=q
2
0
1+t/a
−n
D= D
0
1+t/a
−n−1
(10.5.2)
where a =nq
2
0
/2D
0
n=2/c
7
−2. Early experiments suggest that c
7
=4 and n is in
the range 1.1 to 1.3. Later arguments by Reynolds (1976) suggest that this model works

10.6 Stress-Equation Models 243
best for short wavelength disturbances. If the entire spectrum is included, Reynolds
suggests that an improvement on equation (10.5.2) is
q
2
=
1
m +1
+
3
2
aD
2/3
A
−2/3m +5
D= C
q
2
3m +5/2m +3
(10.5.3)
where m = 2 seems the most reasonable choice. This corresponds to c
7
= 11/3 and
n =6/5 in the previous result.
A number of other models have been introduced, each with pluses and minuses.
A heuristic model by Saffman and Wilcox (1974) introduces a pseudovorticity and
uses the transport equation
D
Dt
=
u
i
x
j
u
i
x
j
−
2
+
x
j
+
T
2
x
j
(10.5.4)
in place of equation (10.2.17). For equation (10.2.15) they use
P =
∗
1
2
u
i
x
j
+
u
j
x
i
u
i
x
j
+
u
j
x
i
1/2
D=
∗
q
2
/2 (10.5.5)
with recommended values
=01638
∗
=03=015
∗
=009c
4
=05 and c
∗
4
=05
This model has been tested against a number of examples and has given reasonable
results—in some cases better than the more theoretical models proposed by others. For
updates, see Wilcox (1998).
Since the two-equation models frequently use equations (10.2.15) and (10.2.17),
which involve the kinetic energy and dissipation, they are frequently referred to in the
literature as k − models. The Saffman-Wilcox model is referred to as a k − model.
10.6 Stress-Equation Models
The one- and two-equation models still require modeling of the various terms in the
equations, and the results are often at best mixed. In view of these difficulties, attention
has also gone back to the original equation for the Reynolds stresses, equation (10.2.15).
For a given mean velocity field, the production term does not need to be modeled, but
the remaining ones do.
The type of modeling needed depends on the flow being studied. For instance, at
high Reynolds numbers the small-scale dissipative structures are practically isotropic,
and it has become customary to use
D
ij
=
2
3
ij
D (10.6.1)
The pressure strain rate term for incompressible flow has the property that
T
ii
=0 (10.6.2)
and for flows with no mean strain rate it is responsible for the return to isotropic
conditions. It is known, however, that for deforming flows the situation is much more
complex, and a number of diverse methods have been proposed to model it. Examples
