Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


224 Flow Stability
0 =
2
n=0
A
n
cosh
c
n
2
+B
n
sinh
c
n
2
0 =
2
n=0
A
n
cosh
c
n
2
−B
n
sinh
c
n
2
0 =
2
n=0
c
n
A
n
sinh
c
n
2
+B
n
cosh
c
n
2
0 =
2
n=0
c
n
−A
n
sinh
c
n
2
+B
n
cosh
c
n
2
0 =
2
n=0
c
2
n
−a
2
A
n
cosh
c
n
2
+B
n
sinh
c
n
2
0 =
2
n=0
c
2
n
−a
2
A
n
cosh
c
n
2
−B
n
sinh
c
n
2
(9.2.25)
These are six homogeneous equations in the six sets of unknown constants A
n
B
n
.
There is only a trivial solution unless the determinant of the coefficients of the A
n
and
B
n
vanishes. In this case the 6 by 6 determinant can be written as the product of two 3
by 3 determinants. The result of the calculation is that either
sinh
c
0
2
sinh
c
1
2
sinh
c
2
2
c
0
cosh
c
0
2
c
1
cosh
c
1
2
c
2
cosh
c
2
2
c
2
0
−a
2
2
sinh
c
0
2
c
2
1
−a
2
2
sinh
c
1
2
c
2
2
−a
2
2
sinh
c
2
2
=0 (9.2.26)
or
cosh
c
0
2
cosh
c
1
2
cosh
c
2
2
c
0
sinh
c
0
2
c
1
sinh
c
1
2
c
2
sinh
c
2
2
c
2
0
−a
2
2
cosh
c
0
2
c
2
1
−a
2
2
cosh
c
1
2
c
2
2
−a
2
2
cosh
c
2
2
=0 (9.2.27)
The first 3 by 3 determinant came from the hyperbolic cosine terms in W and is referred
to as the even disturbance because of the hyberbolic cosine terms in W. The second 3
by 3 determinant came from the hyperbolic sine terms in W and is referred to as the
odd disturbance.
Expansion and simplification of the determinants in equations (9.2.26) and (9.2.27)
give
c
2
0
−a
2
c
0
tanh
c
0
2
+
c
2
1
−a
2
c
1
tanh
c
1
2
+
c
2
1
−a
2
c
2
tanh
c
2
2
=0 (9.2.28)
for even disturbances, and
c
0
coth
c
0
2
+
1+i
√
3
2
c
1
coth
c
1
2
+
−1+i
√
3
2
c
2
coth
c
2
2
=0 (9.2.29)
for odd disturbances. Further simplification is possible by noting that c
0
is pure imaginary
and c
2
is the complex conjugate of c
1
. Therefore, both equations (9.2.28) and (9.2.29)
are real.
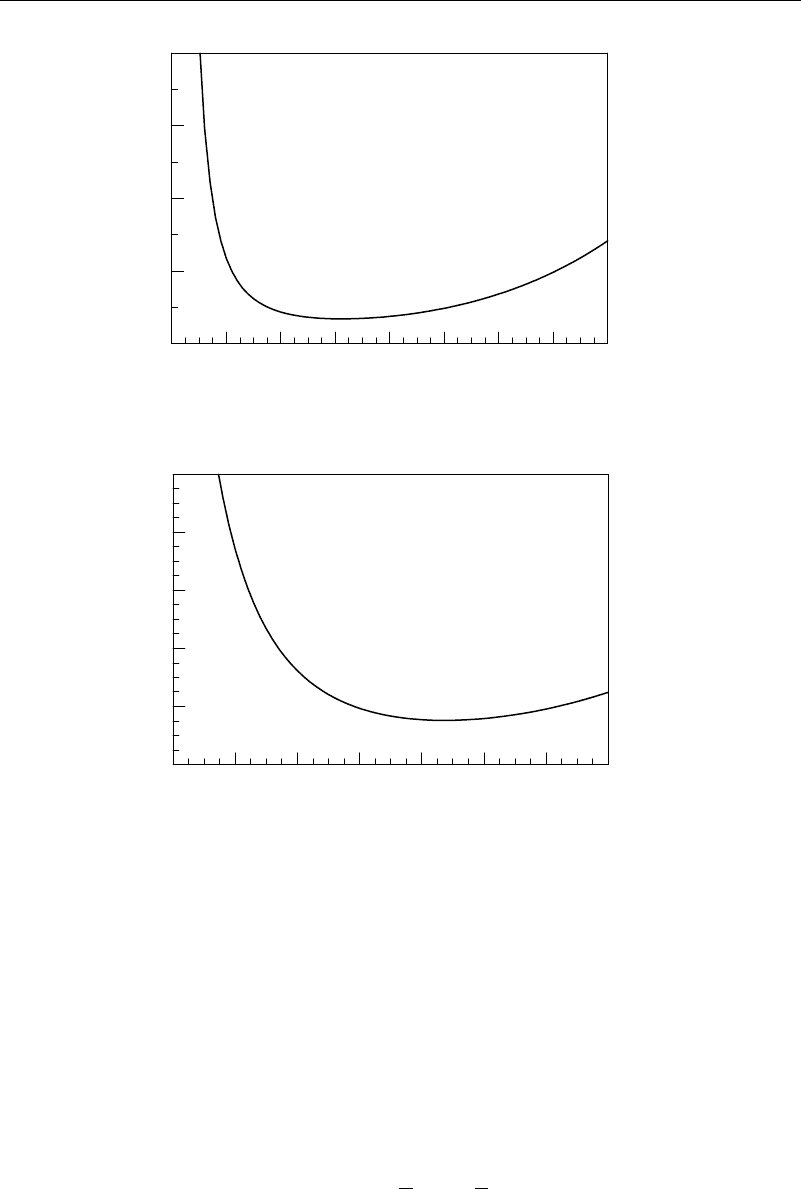
9.2 Thermal Instability in a Viscous Fluid—Rayleigh-Bénard Convection 225
Even disturbances
Rayleigh number
unstable
stable
Wave number
20,000
15,000
10,000
5,000
0
012345678
Figure 9.2.2 Bénard stability curve for even disturbances
60,000
50,000
40,000
30,000
20,000
10,000
1 2 3 4 5 678
Odd disturbances
Rayleigh number
unstable
stable
Wave number
Figure 9.2.3 Bénard stability curve for odd disturbances
Plots of the roots of these equations are shown in Figure 9.2.2 for even disturbances
and Figure 9.2.3 for odd disturbances. Even disturbances occur at the lowest value of the
Rayleigh number—approximately 1,707.76—occurring at a wave number a of 3.117.
For values of the Rayleigh number below this, according to our analysis the disturbances
are all stable. For values of the Rayleigh number above this critical value, there will be
some range of wave number a for which the disturbance will grow. Thus the flow will
be unstable. For odd disturbances, the corresponding values of the critical Rayleigh and
wave numbers are 17,610.39 and 5.365.
Other boundary conditions that have been used in the solution include the case where
the top surface is free Ra
critical
=11007a
critical
=2682 and when both surfaces are
free Ra
critical
=6575 a
critical
=2221.
As yet, the shape factor f has not been found. The actual form of f will be deter-
mined by the plate geometry. There are, in fact, many geometric possibilities for the cell
shape. For instance, f proportional to either sin
ax
b
or sin
ay
b
will give long cylindrical

226 Flow Stability
rollers observed frequently in the atmosphere; f proportional to sin
px
b
sin
qy
b
, where
p
2
+q
2
=a
2
, will give rectangular cells; f proportional to 2 cos
√
3ax
2b
cos
ay
2b
+cos
ay
b
gives
hexagonal cells. Bénard observed hexagonal cells in his experiments, but this shape was
likely due to surface tension on the free surface at the top of his apparatus. The cell
shape is influenced by the boundary shape, and circular rollers can be observed if round
plates are used (Koschmeider, 1993).
Research has shown that the secondary flow just described leads to at least one
further laminar flow if the temperature distance between the plates is increased beyond
the critical limit.
The preceding is an exact solution for the neutrally stable curves for the lin-
ear stability problem. While the computations are tedious, the mathematical questions
encountered are relatively uncomplicated. This generally is not true when the primary
flow is nonquiescent, as shall be seen.
9.3 Stability of Flow Between Rotating Circular
Cylinders—Couette-Taylor Instability
Couette (1890) studied the possibility of using flow between rotating cylinders to
determine the viscosity of liquids. His general formula for the flow in cylindrical polar
coordinates was
v
=Ar +
B
r
(9.3.1)
where
A =
r
2
1
1
−r
2
2
2
r
2
1
−r
2
2
B=−
r
2
1
r
2
2
1
−
2
r
2
1
−r
2
2
(9.3.2)
The subscript 1 refers to the inner cylinder and 2 to the outer cylinder. Couette built an
apparatus with a rotating outer cylinder and an inner cylinder supported on a fine torsion
wire to measure torque. His measurements were not particularly accurate, but he did
notice that as the angular speed was increased, the graph of torque versus angular speed
departed from the straight line expected for laminar flow. His results prompted Rayleigh
(1916b) to examine the flow and find that for the flow to be stable, it is necessary that
r
2
outer
outer
>r
2
inner
inner
(9.3.3)
Since Couette’s apparatus did not meet this criterion, departure of the flow from the
state predicted by equation (9.3.1) was a possibility.
Taylor (1923) constructed an apparatus similar to that used by Couette but that
allowed for visualization of the flow between the cylinders. He also provided a theoretical
stability analysis and thus was able to confirm his findings. The analysis proceeded as
follows.
In the manner used in Rayleigh’s convection problem, a small disturbance is added
to the flow of equation (9.3.1) and introduced onto the Navier-Stokes equations. The
disturbance, based on Taylor’s observations, was taken to be axisymmetric and of
the form
u
r
=ur cos kz e
st
u
=vr cos kz e
st
u
z
=wr sin kz e
st
(9.3.4)

9.3 Stability of Flow Between Rotating Circular Cylinders—Couette-Taylor Instability 227
Insertion of these into the Navier-Stokes equations gives
su −
2V
r
v
=−
dp
dr
+
d
2
u
dr
2
+
1
r
du
dr
−k
2
u −
u
r
2
(9.3.5)
sv +
dV
dr
+
V
r
u
=
d
2
v
dr
2
+
1
r
dv
dr
−k
2
v −
v
r
2
(9.3.6)
sw = kp +
d
2
w
dr
2
+
1
r
dw
dr
−k
2
w
(9.3.7)
along with the continuity condition
du
dr
+
u
r
−kw =0 (9.3.8)
These are to be solved subject to the boundary conditions
u =v =w = 0atr =r
1
and at r = r
2
(9.3.9)
Solution of the system of equations (9.3.5) through (9.3.9) is complicated by the
order of the system (6th), the cylindrical polar coordinates that introduce nonconstant
coefficients and suggest the need for Bessel functions, and also the number of parameters
needed to describe the problem. (Remember that in 1923 the most sophisticated computer
available was an adding machine.) Taylor restricted the problem to the case of small
gap spacing and therefore was able to obtain an approximate solution in terms of
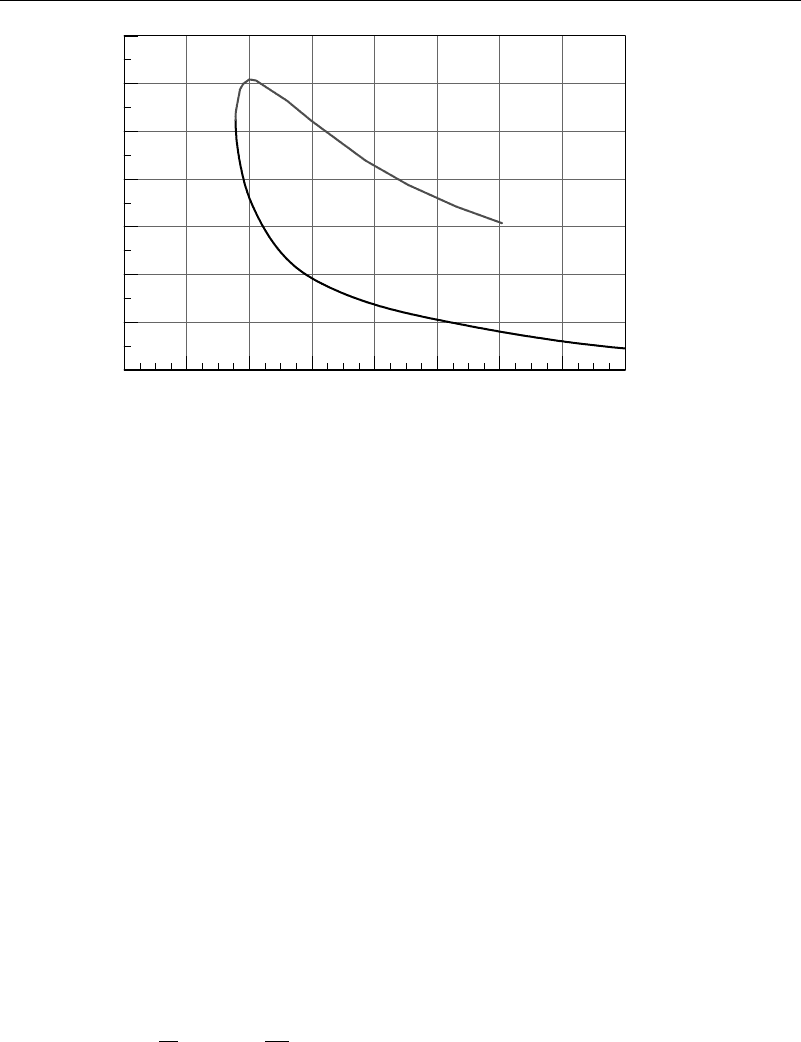
trigonometric and hyperbolic functions. His and later results are shown in Figure 9.3.1.
The dashed line in the lower right-hand corner is the Rayleigh stability criterion. The top
1,800
1,600
1,400
1,200
1,000
800
600
400
200
0
–1,200 –1,000 –800 –600 –400 –200 0 200 400 600
R
inner
Ω
inner
ν
R
outer
Ω
outer
ν
2
2
Figure 9.3.1 Stability curves for Taylor/Couette stability

228 Flow Stability
curve is for r
2
/r
1
= 11. In successive curves this ratio increases by 0.05. The curves
are from empirical formulae in Coles (1967). Taylor’s small-gap theory showed that as
the gap size goes to zero, for the case where the outer cylinder is stationary,
T =Taylor number =
4
r
outer
−r
inner
2
2
r
2
outer
/r
2
inner
−1
≈1708 (9.3.10)
The instability that Taylor observed in Couette flow consisted of a series of stacked
rings, with the flow occurring along helical paths in each ring. The flow is complicated
but still laminar. Subsequent experimenters have found that higher speeds result in the
forming of wavy, ropey cells before turbulent flow is achieved and that the pattern
observed can depend on the history of how the final pattern is obtained. See Koschmeider
(1993) for a summary.
Note that, as in the previous case of convection flow, the cause of the flow is
inertial effects. In this case it is the centrifugal and Coriolis acceleration, as contrasted
with gravity and buoyancy in the Rayleigh problem.
As an interesting sidelight, Taylor, a descendant of George Boole, who discovered
Boolean algebra, on which computer logic is based, was given a lifetime stipend by the
British government upon completing his studies with the freedom to do whatever he
wished in science. He chose to do his work at Cambridge University, where Rayleigh
was located at the time Taylor worked on this problem. Taylor has said that Rayleigh
discouraged him from pursuing this work, as it was “unlikely to be fruitful.” Fortunately,
Taylor did not heed this advice, as it was one of his early successes. Taylor’s collected
works compile six volumes.
While Couette pursued this work initially for viscometric purposes, these types of
flows occur in many other situations. In high-speed situations in instruments such as
gyroscopes it is necessary to maintain constant speed, which may require temperature
control to ensure constant viscosity. This requires an understanding of the heat transfer
occurring in the flow, which differs greatly if the cellular rings form. Other situations
where this type of inertial instability forms are in flows between stationary curved
parallel plates and curved pipes, where similar cellular patterns occur. The curved plate
geometry was investigated by Dean (1928).
9.4 Stability of Plane Flows
The stability of plane flows has a long and interesting history. The equations were first
formulated by Orr (1906–1907), and exact solutions were presented by him for the
special case where the velocity varied linearly between two plates. The results, however,
were indefinite, since even though the solutions were in terms of well-known (but
complicated) functions, the calculations that had to be done were still formidable. Later
efforts by such famous physicists as Sommerfeld (1908) and Heisenberg (1924) found
asymptotic solutions for the stability of two-dimensional flow between parallel plates.
Their results were incorrect because of the difficult nature of the solution, involving
the proper way to traverse turning points. The first successful asymptotic solution was
by C. C. Lin (1945). His theoretical results were confirmed by a series of elaborate
experiments performed at the National Bureau of Standards by Schubauer and Skramstad
(1943). Since that first successful analysis, with the advent of digital computers and
guided by Lin’s results, numerical solutions have produced more accurate numerical
results without the need for elaborate asymptotic analysis.

9.4 Stability of Plane Flows 229
The physical nature of the instability of parallel flows is quite different than for the
Rayleigh-Bénard instability just studied. Here, the disturbance is of the form of a trav-
eling wave rather than a standing cellular pattern. For plane Poiseuille flow with plates
at y = 0 and y = b, the primary flow is v = Uy 0 0, with Uy =U
m
y/b −y
2
/b
2
and a pressure P =−vxU
m
/b
2
. Take a disturbance of the form u
x y t v
x y t 0,
where
u
x y t =uye
ikx−ct
v
x y t =vye
ikx−ct
(9.4.1)
and
p
x y t =pye
ikx−ct
The preceding is a two-dimensional disturbance that is sufficient to study the stability of
this flow, since it was shown by Squire (1933) that two-dimensional disturbances always
became unstable at lower Reynolds numbers than do three-dimensional disturbances.
Here, c =c
r
+ic
i
, where c
r
is the speed at which the wave travels in the x direction, and
kc
i
is the growth rate of the disturbance. If kc
i
< 0, the disturbance decreases with time
and the wave is stable.Ifkc
i
> 0, the wave grows with time and there is instability.If
kc
i
=0, the wave neither grows nor decays with time, and there is neutral stability.
From substituting this form for the velocities into the incompressible continuity
equation in the form
U +u
x
+
v
y
=0
find that
iku
=−
v
y
(9.4.2)
The applicable Navier-Stokes equations for this flow are
U +u
t
+U +u
U +u
x
+v
U +u
y
=−
P +p
x
+
2
U +u
x
2
+
2
U +u
y
2
v
t
+U +u
v
x
+v
v
y
=−
P +p
y
+
2
v
x
2
+
2
v
y
2
Substituting the forms of equation (9.4.2), subtract out the terms from the primary flow
equilibrium
0 =−
P
x
+
2
U
y
2
Linearizing any terms of order greater than the first in u, v, and p, we are left with
−ikcu +Uiku +v
dU
dy
=−ikp +
d
2
u
dy
2
−k
2
u
(9.4.3)
and
−ikcv +Uikv
=−
dp
dy
+
d
2
v
dy
2
−k
2
v
(9.4.4)
230 Flow Stability
Solving for the pressure p from equation (9.4.3) gives
ik
p
=
d
2
u
dy
2
−k
2
u
−ikU −cu −
dU
dy
(9.4.5)
Differentiating this expression for p with respect to y and using the result together with
equation (9.4.4) to eliminate p and u, after some rearrangement the result is
d
2
dy
2
−k
2
d
2
dy
2
−k
2
v = ikU −c
d
2
dy
2
−k
2
v −ik
d
2
U
dy
2
v (9.4.6)
This is to be solved subject to the boundary conditions u =v =0aty =0 and y =b,or
equivalently,
v =
dv
dy
=0aty = 0 and at y = b (9.4.7)
If equation (9.4.6) is made dimensionless by letting U
=U/U
m
c
=c/U
m
k
=kb
=y/b, and Re = U
m
b/, the result is
d
2
d
2
−k
2
2
v = ik
Re
U
−c
d
2
d
2
−k
2
v −v
d
2
U
d
2
(9.4.8)
with the boundary conditions
v =
dv
d
=0at =0 and at = 1 (9.4.9)
This dimensionless form of the stability equation for parallel flows is referred to as
the Orr-Sommerfeld equation. It is also used as an approximation for nearly parallel
flows, such as the flow in a boundary layer. (Notice that in the preceding dimensionali-
zation U
m
was any convenient velocity—that is, either the mean or maximum of U or
any other value could in fact be used.)
The differential equation (9.4.8) and the boundary conditions of equation (9.4.9)
are all homogeneous, so there is only the trivial solution v = 0, except for special
combinations of the parameters R k
, and c
. These combinations are what must be
determined to answer the flow stability question.
At first glance, the solution of equation (9.4.8) may not appear to be all that difficult.
The equation is fourth order, compared to the sixth-order equations governing Rayleigh-
Bénard and Couette stability. There are, however, two important differences in the two
problems that far outweigh the difference in order. One is the fact that the coefficients
in the equation are no longer constant U
= U
y. The second, less obvious one is
that the real part of the coefficient U
−c
can, and in fact does, change sign in the
region 0 ≤ ≤1 for the conditions of interest. If you think of the difference between the
solutions of the two more familiar equations y
+y =0 (simple harmonic oscillations)
and y
−y = 0 (exponential behavior), it can be imagined that both behaviors are
represented in various parts of the y region. The disturbance in fact tends to be fairly
rapidly oscillating between the walls and where U
= c
r
(this is, of course, the place
where momentum transfer between the primary flow and the disturbance is easiest), and
more gradually varying in the central core.
Viscosity in these flows plays a dual role. On the one hand, it has its traditional
dissipative role, whereby it dissipates the energy of the disturbance. The second role of
viscosity is to set up phase differences between the pressure and the various velocity
Problems—Chapter 9 231
1.4
1.2
1.0
0.8
0.6
k
2
Re
1/3
0.4
0.2
0.0
0 1020304050607080
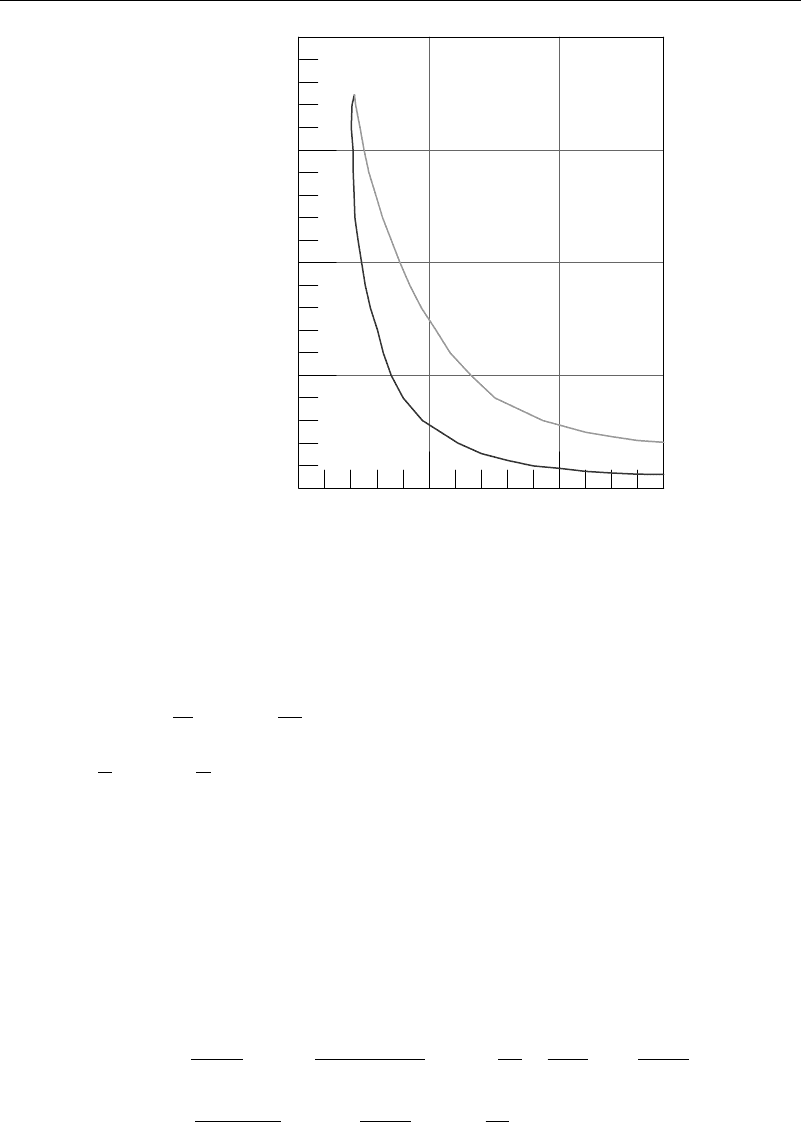
Figure 9.4.1 Stability curve for plane Poiseuille flow
components that enhance the energy transfer from the primary flow. It is this role that
is responsible for allowing the growth of the instability. Experimentally it is known that
the instability that occurs is a transition from laminar flow to turbulent flow.
The technical details of the asymptotic solutions are more complicated than can
be dealt with here. See Lin’s works listed in the References for more details. Use
of matched asymptotic expansions to compute higher-order terms in the asymptotic
expansion are given in Graebel (1966). A plot of the neutral stability curve k
2
versus
Re
1/3
for plane Poiseuille flow is given in Figure 9.4.1. Inside the curve the flow is
unstable, while outside it is stable. The minimum value of Re is approximately 5,772
at a dimensionless wave number of 1.0206.
A similar curve for the Blasius boundary layer profile is given in Figure 9.4.2.
The figure is based on data in Shen (1954), which was found to agree well with the
classic experiments of Schubauer and Skramstad (1947) at the U.S. Bureau of Standards.
Their experiments used a wand that oscillated at a variable rate as a disturbance
source. R
1
is a Reynolds number based on boundary layer thickness as introduced by
Lin (1946). The minimum Reynolds number for stability was found by Shen to be
about 416.
Problems—Chapter 9
9.1 If viscous terms on equation (9.4.5) are neglected, the Orr-Sommerfeld equation
becomes U −c
d
2
v
dy
2
−k
2
v
−
d
2
U
dy
2
v = 0, with fa = fb = 0. (This is sometimes
called the Rayleigh equation.) The real part of the complex number c is the wave speed.
The imaginary part relates to the rate of growth or decay of the disturbance. Because
of the difficulty in solving the full Orr-Sommerfeld equation, much early work was
done on the inviscid version. The problem is complicated that U −c likely has a zero
somewhere in the interval. To investigate this, first divide the inviscid equation by
U −c. Next, multiply it by v
∗
, the complex conjugate of v, and then integrate over the
232 Flow Stability
400
300
200
100
1,000
Re
1
(
ωμ
⁄
ρ
U
2
)
×
10
6
2,000
Figure 9.4.2 Stability curve for Blasius flow
range—say, a to b. Form positive-definite integrals, and then, after splitting into real
and imaginary parts, make some conclusions concerning c.
9.2 An alternate approach to solving the preceding Rayleigh equation
U −c
d
2
v
dy
2
−k
2
v
−
d
2
U
dy
2
v = 0 was introduced by Howard (1961). He first made
the change of variables f = c − Uv. Then the Rayleigh equation becomes
d
dy
c −U
2
df
dy
−k
2
c −U
2
f = 0. To investigate this, multiply it by f
∗
, the complex
conjugate of f , and then integrate over the range—say, a to b. Form positive-definite
integrals, and then, after splitting into real and imaginary parts, make some conclusions
concerning c.
9.3 Show that the equations governing stability of flow between rotating cylinders
(Couette-Taylor instability, equations 9.3.5, 9.3.6, 9.3.7) reduce to
D
2
−
2
−sRv =2RA
u
D
2
−
2
−sRD
2
−
2
u =2
2
Rv
where
k =
r
1
r
2
−r
1
R=
1
r
2
−r
1
2
=
A
1
+
B
r
2
1
1
1+
r
2
−r
1
r
1
−2
=
r
2
−r
1
2
s =
r −r
1
r
2
−r
1
D=
d
d
and A and B are as in equation (9.3.2). To aid in your analysis, let =r
2
−r
1
/r
1
be
a very small parameter.

Chapter 10
Turbulent Flows
10.1 The Why and How of Turbulence 233
10.2 Statistical Approach—One-Point
Averaging 234
10.3 Zero-Equation Turbulent Models 240
10.4 One-Equation Turbulent Models 242
10.5 Two-Equation Turbulent Models 242
10.6 Stress-Equation Models 243
10.7 Equations of Motion in Fourier
Space 244
10.8 Quantum Theory Models 246
10.9 Large Eddy Models 248
10.10 Phenomenological Observations 249
10.11 Conclusions 250
tur-bu-lence (circa 1598): the quality or state of being turbulent: as a: wild com-
motion b: irregular atmospheric motion esp. when characterized by up-and-down
currents c: departure in a fluid from a smooth flow.
tur-bu-lent (1538) 1: causing unrest, violence, or disturbance 2 a: characterized
by agitation or tumult; TEMPESTUOUS b: exhibiting physical turbulence
turbulent flow (circa 1922): a fluid flow in which the velocity at a given point
varies erratically in magnitude and direction; compare LAMINAR FLOW
10.1 The Why and How of Turbulence
These dictionary definitions lay out the problems with the study of turbulent flow:
wild, commotion, irregular, unrest, violence, disturbance, agitation, tumult, tempestuous,
erratic. To that list could be added adjectives such as chaotic, random, confused,
unorganized—well, you see the point. Clearly, while the study of laminar flow is
difficult, the study of turbulent flow requires a completely different approach.
Experience tells us that turbulence is often, but not necessarily, associated with high
Reynolds numbers and is all too common in the atmosphere, oceans, rivers, lakes—even
the plumbing in our buildings and our bodies. Sometimes it serves good purposes. If
you want to mix together two liquids, cool off your coffee by stirring, or stir a can of
paint, the introduction of turbulence comes in handy. On the other hand, if you want
233
