Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.

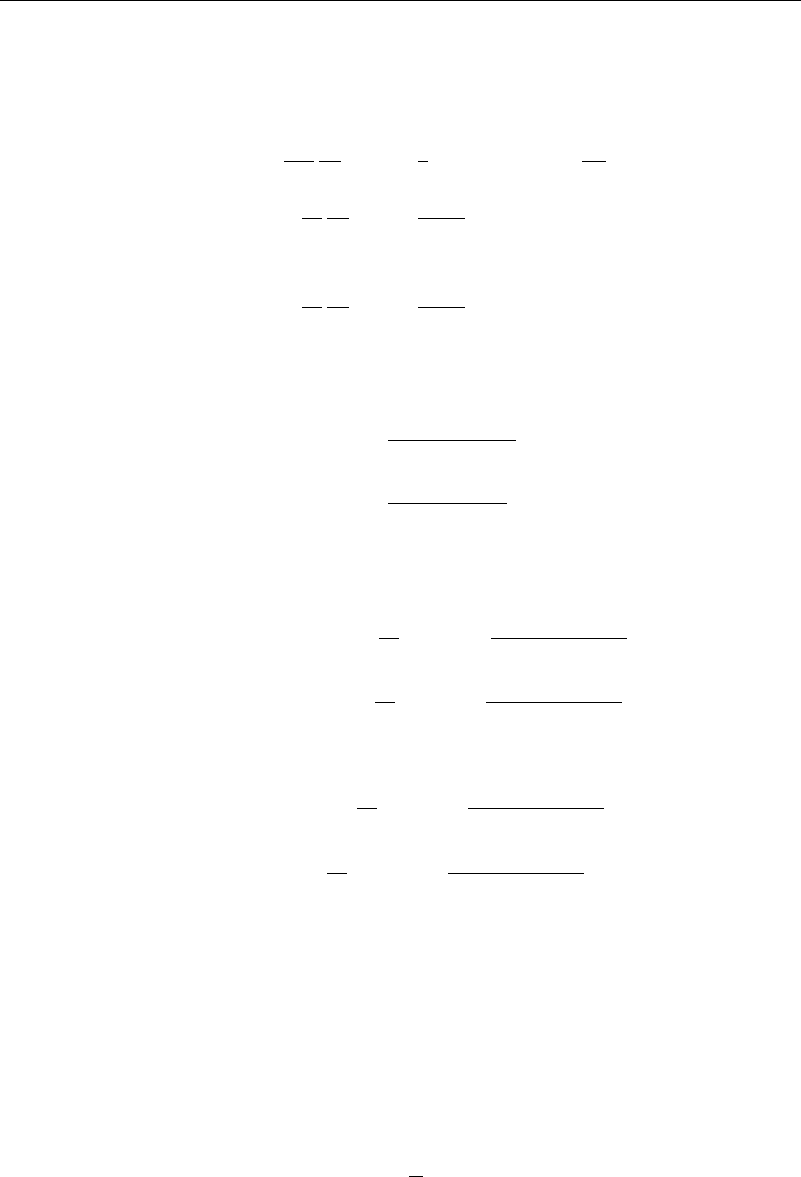
204 Thermal Effects
These satisfy the constant temperature and no-slip conditions at the wall. Both are zero
and have zero derivatives at the edge of the boundary layer, meaning that the shear
stress and heat flux are both zero there.
Substituting these forms into equation (7.8.1) and (7.8.2) yields
1
105
d
dx
u
2
=
1
3
gT
wall
−T
−
u
1
30
d
dx
u
=
2k
0
c
p
(7.8.5)
1
30
d
dx
u
=
2k
0
c
p
(7.8.6)
From previous results it seems reasonable to assume that u and both behave as
powers of x. Choose = Cx
m
, and substitute this into equation (7.8.7) to find
u
x
=
60kx
−m+1
−m +1
0
c
p
C
or
u
x
=
60x
−2m+1
1−m Pr C
2
(7.8.7)
Substituting this into equation (7.8.5), and requiring that the power of x in each term is
the same, gives m =1/4. With this at hand, the constant C can be found to be
C =240
1/4
Pr
−1/2
20
21
+Pr
1/4
2
gT
wall
−T
2
−1/4
=3936Pr
−1/2
20
21
+Pr
1/4
2
gT
wall
−T
2
−1/4
(7.8.8)
Then
=3936Pr
−1/2
20
21
+Pr
1/4
2
gT
wall
−T
2
−1/4
x
1/4
(7.8.9)
u
x
=5164
20
21
+Pr
−1/2
2
gT
wall
−T
2
1/2
x
1/2
(7.8.10)
7.9 Temperature Distribution in an Axisymmetric Jet
The solution for a submerged jet given in Section 5.4.5 can have a temperature distri-
bution added to it. Let
Q =2c
p
0
v
x
TR
2
sin d (7.9.1)
be the total heat flux in the jet, and also let the temperature be given in the form
TR =
1
R
G = cos (7.9.2)

Problems–Chapter 7 205
The energy boundary layer equation then becomes
c
p
df
d
G +f
dG
d
=k
d
d
1−
2
dG
d
(7.9.3)
Here, the stream function f is as given in Section 5.4.5. The boundary conditions to be
applied to G are
dG
d
=0at =0 and = (7.9.4)
These conditions ensure that there is no heat transfer across the axis of the jet.
Equation (7.9.3) can be integrated once to give
1−
2
dG
d
=Pr fG (7.9.5)
and again to give
G =A
a
a +1−
Pr
(7.9.6)
where equation (5.4.31) has been used for f . The constant of integration in equation
(7.9.5) was chosen as zero to satisfy the condition on =0.
The second constant of integration, A, is determined from equation (7.9.1) to be
A =Q/2c
p
1
−1
df
d
Gd. Since f and G are both known and are relatively simple,
the integration can be carried out, giving, finally,
A =
Q
4c
p
a +2
2Pr+1
1−
a
a +2
2Pr+1
−
a
2Pr−1
1−
a
a +2
2Pr−1
(7.9.7)
In the special case where a 1, this simplifies to
A Q
2Pr+1
8c
p
(7.9.8)
Problems—Chapter 7
7.1 A point source of heat such as a candle produces a rising thermal plume. Using
cylindrical polar coordinates and starting with the basic boundary layer equations in
the form
v
r
r
+
v
r
r
+
v
z
z
=0
v
r
v
z
r
+v
z
v
z
z
=
2
v
z
r
2
+
1
r
v
z
r
+ −
g
c
p
v
r
T
r
+v
z
T
z
=k
2
T
r
2
+
1
r
T
r
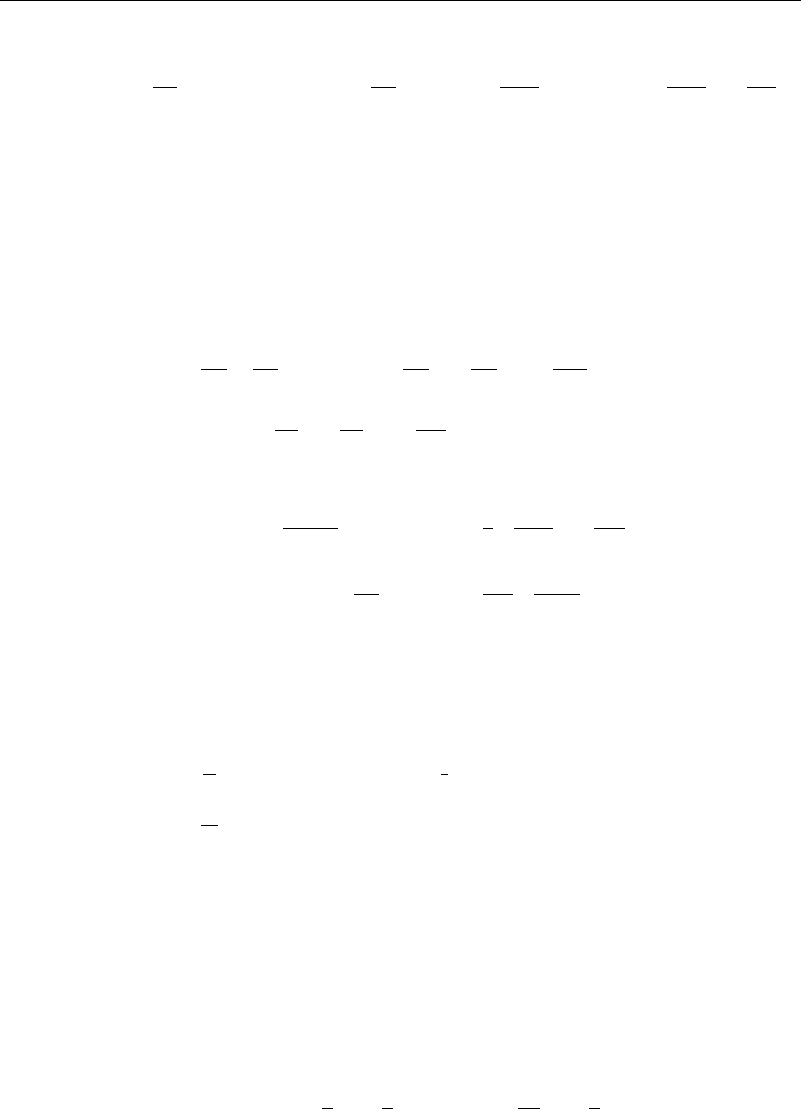
206 Thermal Effects
show that a similarity solution can be found in the form
=
4
f −
g =g
d
dT
T −T
=
G
z
=
2
G
4
3
1/4
r
z
1/4
Here, G is a constant related to the strength of the heat source, defined by
G =
0
2rv
z
−
gdr
Give the similarity equations and the boundary conditions. Do not solve the equations.
(Closed form solutions have been found for Prandtl numbers of 1 and 2.)
7.2 A line source of heat produces a rising thermal plume in the form of a sheet.
Using Cartesian coordinates and starting with the basic boundary layer equations in
the form
v
x
x
+
v
y
y
=0
v
x
v
x
x
+v
y
v
x
y
=
2
v
x
y
2
+ −
g
c
p
v
x
T
x
+v
y
T
y
=k
2
T
y
2
show that a similarity solution can be found in the form
=
Gx
3
2
3
1/5
f =
1
5
2
G
4
3
1/5
y
x
2/5
−
g =g
d
dT
T −T
=
1
125
3
G
4
x
3
2
1/5
Here, G is a constant related to the strength of the heat source, defined by G =
−
v
x
−
gdy. Give the similarity equations and the boundary conditions. Do not
solve the equations. (Closed form solutions have been found for Prandtl numbers of 5/9
and 2.)
7.3 For a plane Poiseuille flow between parallel planes, the velocity distribution is
v
x
=U
0
1−
y
2
a
2
+U
lower
+
U
upper
−U
lower
y
a
. Find the temperature distribution including
the effects of dissipation. The upper wall temperature is T
wall
, and the lower wall heat
flux is q = k
dT
dy
.
7.4 A horizontal semi-infinite plate is submerged in a uniform stream of a very low
Prandtl number fluid (a liquid metal). The fluid is at a temperature of T
with constant
properties, and the wall is maintained at a constant temperature T
wall
. Using the integral
method with a temperature distribution in the form T = A +B sinCy, find A B, and
C; the thermal boundary layer thickness; and the heat transfer at the wall. (Hint: The
very low Prandtl number means that the thermal boundary layer is much thicker than
the momentum boundary layer.)
7.5 Use the integral method and the following velocity and temperature profiles to
find the boundary layer on a vertical flat plate with constant heat flux q.
v
x
=u
y
1−
y
2
T= T
+
q
2k
1−
y
2
Hint: As in the temperature-specified natural convection case, expect that u and will
be of the form of powers of x.

Chapter 8
Low Reynolds Number Flows
8.1 Stokes Approximation 207
8.2 Slow Steady Flow Past a Solid
Sphere 209
8.3 Slow Steady Flow Past a Liquid
Sphere 210
8.4 Flow Due to a Sphere Undergoing
Simple Harmonic Translation 212
8.5 General Translational Motion of
a Sphere 214
8.6 Oseen’s Approximation for Slow
Viscous Flow 214
8.7 Resolution of the Stokes/Whitehead
Paradoxes 216
Problems—Chapter 8 217
Flows that occur at small values of the Reynolds number are important for studying the
swimming of microorganisms, motion of small particles, determining the viscosity of
suspensions, motion of glaciers, micro- and nanotechnology, and many other applica-
tions. The mathematical difficulties involved are somewhat subtler than those found in
large Reynolds number flows but are fundamentally much the same.
8.1 Stokes Approximation
For very small values of the Reynolds number Stokes (1851) proposed that the convec-
tive acceleration terms could be neglected and the Navier-Stokes equations replaced by
v
t
=−p +
2
v (8.1.1)
·v = 0
Taking the divergence of the first of equation (8.1.1) gives
2
p = 0 (8.1.2)
and taking the curl gives
t
=
2
with = ×v (8.1.3)
207
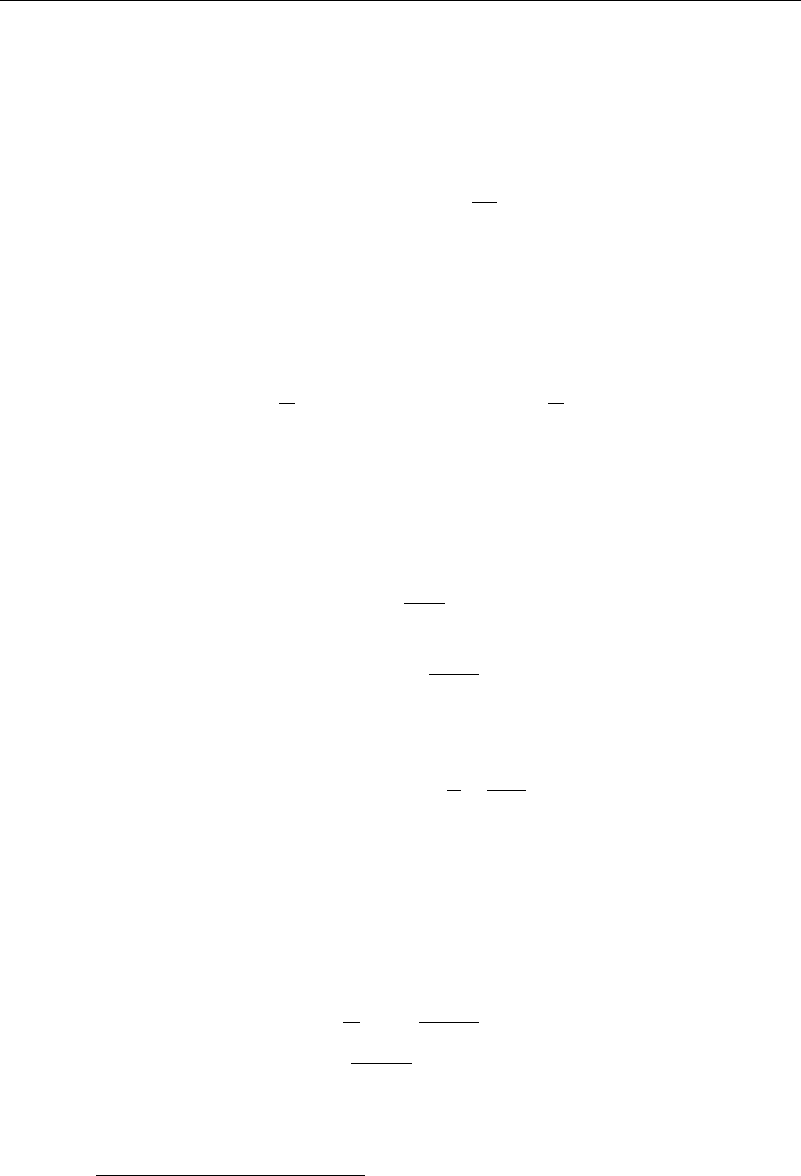
208 Low Reynolds Number Flows
If the time dependence of the velocities is of the form e
t
, then it follows from
equation (8.1.1) that
p =
2
v −v (8.1.4)
Since the pressure satisfies Laplace’s equation, a particular solution of equation (8.1.4)
is then
v
particular
=−
1
p (8.1.5)
This is useful in solving for pressure once the velocity is known.
Stokes originally solved the problem of flow about a sphere in terms of the stream
function. Lamb (1932) presented a general solution for the pressure in terms of a Taylor
series. He also presented a general solution for the velocity in the form
vR = + × ×A +R × where
2
=0
t
−
2
2
A =0 and
t
−
2
=0
(8.1.6)
Since attention will be restricted here to simple geometries, these three approaches
are too complicated for our purposes. Instead, Stokes original solution supplies three
fundamental solutions of equation (8.1.1): a doublet, a stokeslet, and a rotlet.
1
1. Doublet. This is the same doublet as that found previously for irrotational inviscid
flow—namely,
r =
A·R
R
2
R = xi +yj +zk (8.1.7)
Its velocity is given by v = =
A×R
R
3
. Here, A is a vector that can either be
constant or a function of time.
2a. Stokeslet for steady flows. The velocity field
v =
B
R
+
B·R
R
3
R (8.1.8)
where B is a constant vector, satisfies the time-independent case of (8.1.1). It
corresponds to the second term in (8.1.4). It contributes a force on a body, but
not a moment.
2b. Stokeslet for unsteady flows. The velocity vector
v = e
−ik
2
t
−B
2
f +
B·
f
where
f =
1
k
2
ik +
1−e
ikR
R
(8.1.9)
and where k = 1 +i
√
/2 and B are constants, satisfies equation (8.1.1)
for unsteady flows. The form for f has been chosen so that in the limit as k
approaches zero, the steady-state form equation (8.1.8) is recovered.
1
The terms Stokeslet and rotlet were coined in the later half of the twentieth century.

8.2 Slow Steady Flow Past a Solid Sphere 209
3a. Rotlet for steady flows. The velocity vector
v = R ×
C·R
R
3
(8.1.10)
where C is a constant vector, has been termed a rotlet. There is no pressure field
associated with it, nor does it contribute to the force acting on a body. It can,
however, exert a turning moment on a body.
3b. Rotlet for unsteady flows. The velocity vector
v = R ×
C·R
R
3
h
where h =e
ikR−k
2
t/
1−ikR (8.1.11)
satisfies equation (8.1.1) for unsteady flows. Notice that in the limit as k
approaches zero, this velocity becomes equal to that given in equation (8.1.10).
8.2 Slow Steady Flow Past a Solid Sphere
For slow flow past a sphere of radius a, Stokes superimposed a uniform stream, doublet,
and stokeslet, all oriented in the z direction. Thus,
v = U k +B
1
R
2
R
z
+C × ×kR
=
U +
1
R
3
B −
1
R
C
k +
−
3z
R
5
B −
z
R
3
C
R
(8.2.1)
On R =a the velocity must vanish. Thus,
1
a
3
B −
1
a
C =−U −
3
a
5
B −
1
a
3
C =0
yielding
B =−
a
3
4
U C =
3a
4
U
Thus,
v = U
1−
a
3
4R
3
−
3a
4R
k +U
3a
3
z
4R
4
−
3az
4R
2
e
R
=U
1−
3a
2R
+
a
3
2R
3
e
R
cos +U
−1+
3a
4R
+
a
3
4R
3
e
sin
(8.2.2)
From this and equation (8.1.1) the pressure can be found as
p = p
0
−
3a
2R
2
U cos (8.2.3)
and the stress components as
RR
=−p +2
v
R
R
=U
9a
2R
2
−
3a
3
R
4
cos
R
=
1
R
v
R
+
v
R
−
v
R
=−
3a
3
2R
4
U sin
(8.2.4)

210 Low Reynolds Number Flows
On the surface of the sphere, these stresses become
RR
a
=
3
2a
U cos
R
a
=
−
3a
3
2a
U sin The force on the sphere is thus given by
F
z
=
0
RR
cos −
R
sin 2R sin
a
ad
=3aU
0
cos
2
+sin
2
sin d (8.2.5)
=6Ua
The preceding solution has had many uses. Perhaps the most noteworthy was
determination of the charge on an electron by Robert A. Millikan, who was awarded
the 1923 Nobel Prize in physics for his work. First he sprayed a few tiny drops of oil
between two parallel plates. He then measured the diameter of the drops and, using the
fact that F
drag
= Weight −Buoyant Force, determined the diameter of the drops. He
then applied an electric charge on the plates in a direction opposite to gravity and again
measured velocity. The electric charge induces a force qE/D, where q is the charge on
the electron, E is the strength of the electric field, and D is drop diameter. Since the
number of electrons attached to a given drop is unknown, a number of measurements
had to be taken. The experiment does not give an exact answer, since because of small
droplet size Brownian motion causes an appreciable percentage of error. Nevertheless,
his results gave a far more accurate estimate than was previously obtainable.
Stokes’s result for the force on a sphere is also used in viscometry. By dropping
a small sphere of known diameter in a fluid and measuring the terminal velocity, the
viscosity can be deduced.
Einstein (1906, 1911) also used Stokes’s equations to provide an estimate of the
viscosity of dilute suspensions. He found that the equivalent viscosity was given by
equivalent
=
fluid
1+25 where =
4
3
R
3
c =
volume of spheres
volume of suspension
Here, c is the concentration of the suspended material. (The preceding formula is a cor-
rected version of Einstein’s results, as found in the text by Landau and Lifshitz (1959)).
When there are clusters of spheres falling in a fluid—an unusual behavior where
some particles pass others and the passed particles speed up and pass the original
passers—has been observed and explained in part using Stokes’s solution for the drag
force (Hocking, 1964).
8.3 Slow Steady Flow Past a Liquid Sphere
A result similar to the preceding for liquid spheres is also useful, as was demonstrated by
Millikan’s experiments. Expect that equation (8.2.1) can be used outside of the sphere,
but because it is infinite at the origin, a different nonsingular solution must be found
inside the sphere. Also, the doublet and stokeslet are not applicable inside the sphere
for the same reason. The rotlet can be used if C is chosen as
C =
1
6
k
x
2
+y
2
2
+15z
2
x
2
+y
2
−
13
3
z
4
(8.3.1)

8.3 Slow Steady Flow Past a Liquid Sphere 211
This satisfies equation (8.1.1) and has the velocity field ze
r
−2 r
2
k expressed in cylin-
drical polar coordinates. Then, using this rotlet plus a uniform stream of strength D in
the z direction, the result is
v =
⎧
⎪
⎨
⎪
⎩
U −
2B
R
3
−
C
R
cose
R
+
−U −
B
R
3
+
C
R
sin e
R≥a
D −R
2
E
cose
R
+
−D +2R
2
E
sin e
R≤a
(8.3.2)
Requiring that both of the v
’s be the same at R =a gives U +
B
a
3
−
C
a
=D −2a
2
E.
Requiring that both of the v
R
’s be zero at R =a (so that the sphere does not change
in size) gives
U −
2B
a
3
−
C
a
=D −a
2
E = 0
Thus
B = a
3
U −Ca
2
D=−
3U
2
+
C
4a
E=−
3U
2a
2
+
C
4a
3
(8.3.3)
The constant C is determined by requiring that
R
be continuous on the surface of
the sphere. Using
R
=
1
R
v
R
+
v
R
−
v
R
gives
C =−
Ua
3
4
inner
inner
+
outer
(8.3.4)
Then
v =
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
U cos
1−
2
outer
+3
inner
outer
+
inner
a
2R
+
inner
outer
+
inner
a
3
2R
3
e
R
+U sin
−1+
2
outer
+3
inner
outer
+
inner
a
4R
+
inner
outer
+
inner
a
3
4R
3
e
for R ≥a
outer
2
outer
+
inner
U
cos
R
2
a
2
−1
e
R
+sin
1−
2R
2
a
2
e
for R ≤a
(8.3.5)
The portion of the pressure field is found by substituting equation (8.3.5) into
the steady form of equation (8.1.2). A body force must be included to provide the
mechanism for the flow. Here, gravity has been chosen as the most common body force.
The result is
p =
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
cos
−U
outer
2
a
R
3
2
inner
+3
outer
inner
+
outer
−
outer
Rg
for R ≥a
cos
U
5
outer
inner
inner
+
outer
R
a
2
−
inner
Rg
for R ≤a
(8.3.6)
Having the velocity field, the stresses can be found as
R
=
R
−
R
+
1
R
R
=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
−3U
outer
inner
2
outer
+
inner
a
3
R
4
sin R ≥a
−3U
outer
inner
2
outer
+
inner
R
a
2
sin R ≤a
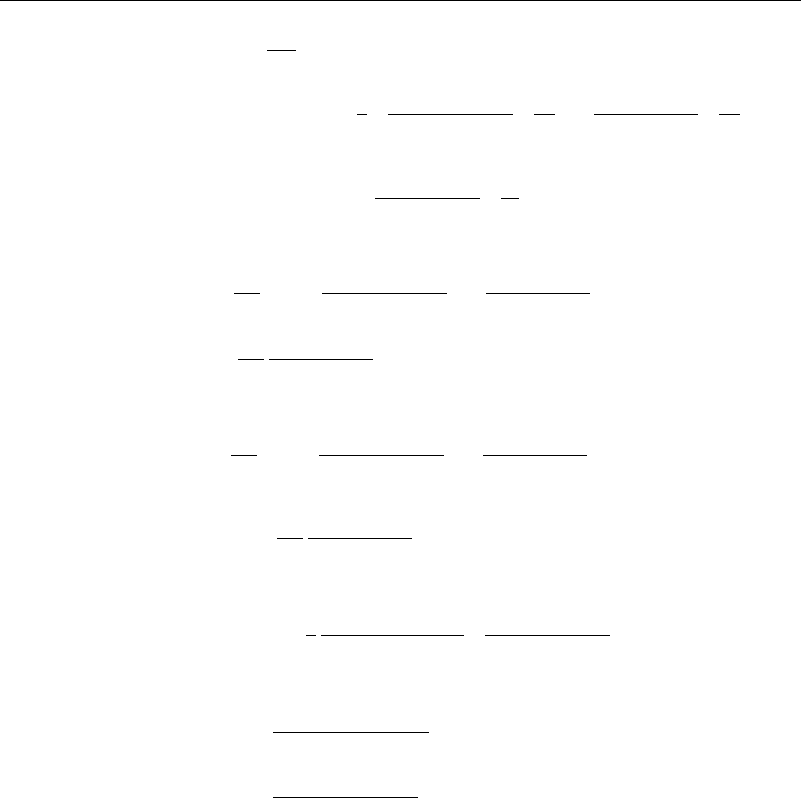
212 Low Reynolds Number Flows
RR
=−p +2
R
R
=cos
⎧
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎩
3
outer
U
1
2
2
outer
+3
inner
outer
+
inner
a
R
2
−
inner
outer
+
inner
a
3
R
4
+
outer
Rg R ≥a
−3
outer
U
inner
outer
+
inner
R
a
2
+
inner
Rg R ≤a
Therefore, on R =a,
RR
=cos
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
3U
2a
outer
2
outer
+3
inner
outer
+
inner
−
inner
outer
outer
+
inner
−
outer
ag R =a+
−
3U
a
outer
inner
outer
+
inner
−
inner
ag R =a −
Requiring the two forms of the normal stress
RR
be the same at R =a gives
3U
2a
outer
2
outer
+3
inner
outer
+
inner
−
inner
outer
outer
+
inner
−
outer
ag
=−
3U
a
outer
inner
outer
+
inner
−
inner
ag
yielding for the liquid sphere’s terminal velocity
U =
2
3
outer
−
inner
a
2
g
outer
outer
+
inner
2
outer
+3
inner
(8.3.7)
Limiting cases of this which are of interest are
U →
2ga
2
outer
−
inner
9
outer
as
inner
→(solid sphere) (8.3.8)
U →
ga
2
outer
−
inner
3
outer
as
inner
→0 (vapor sphere).
In the preceding analysis, surface tension has been neglected because the com-
bination of a perfectly spherical liquid drop and surface tension is incompatible with
gravity. Generally speaking, providing the Reynolds numbers are small, surface tension
will play a minor role. However, for very small gas bubbles rising in a liquid, it has
been found that their velocity is closer to that predicted for a solid sphere rather than the
second of equation (8.3.8). In this case, it is believed that the presence of surface-active
impurities in the liquid can form a mesh of large molecules on the interface, causing it
to behave like a rigid surface (Levich, 1962).
8.4 Flow Due to a Sphere Undergoing Simple
Harmonic Translation
If a solid sphere undergoes simple harmonic motion along the z-axis in a fluid that is
otherwise at rest, the flow can be described by a stokeslet-doublet combination. A stream
function approach can be used and the development in Lamb (1932, page 643) followed.
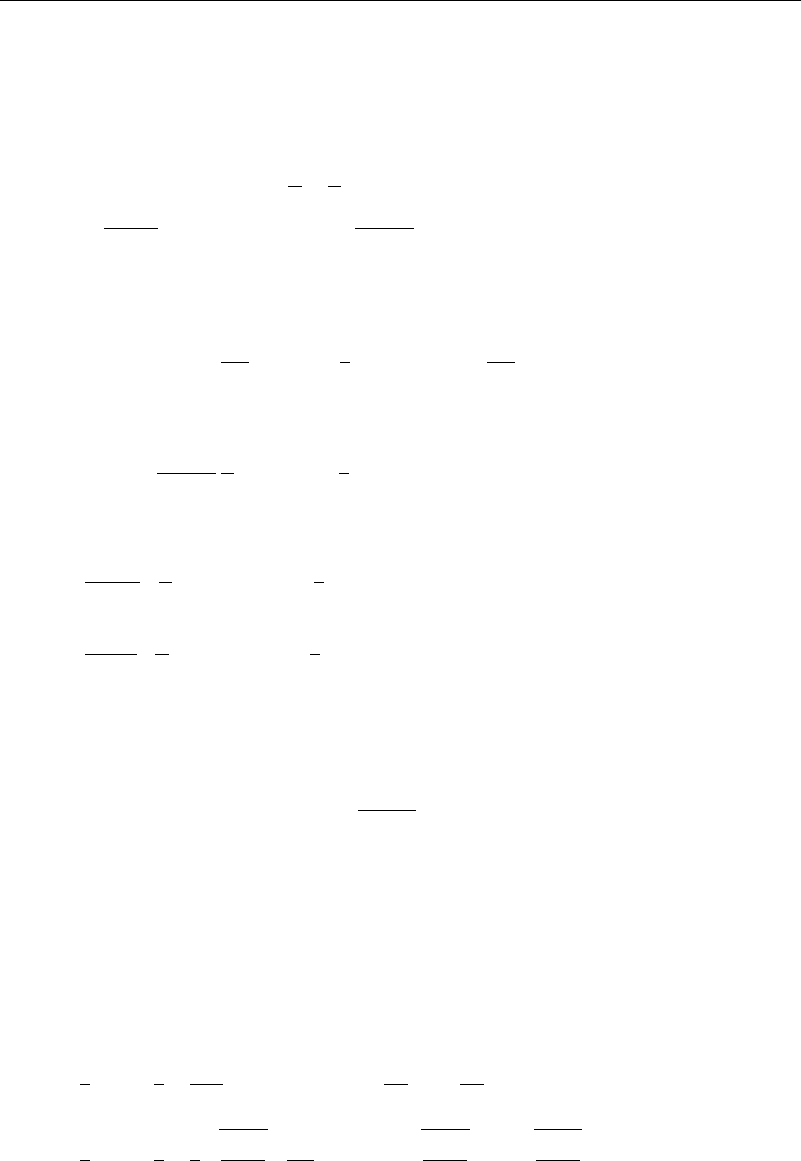
8.4 Flow Due to a Sphere Undergoing Simple Harmonic Translation 213
The calculations are a bit lengthy, so to simplify things, complex numbers are used for
the stream function, velocity components, and stresses, with the understanding that the
real portions of the expressions are intended.
Inserting the general form = sin
2
frU with U = U
0
e
it
into equation (8.1.1)
gives solutions
fR =
A
R
+
B
R
1+kRe
−kR−a
Here, k =
√
i/ = 1 +i with =
√
/2. In obtaining solutions of equation
(8.1.1) those portions that die out as R becomes large have been selected.
Applying the no-slip boundary conditions on the surface of the sphere, the constants
A and B are found to be
A =
3a
2k
2
1+ka +
1
3
k
2
a
2
B=−
3a
2k
2
giving
=
3sin
2
2k
2
a
R
1+ka +
1
3
k
2
a
2
−1 +kRe
−kR−a
U (8.4.1)
This yields velocity components
v
R
=
3cos
k
2
a
2
a
R
3
U
1+ka +
1
3
k
2
a
2
−
1+kR
e
−kR−a
v
=
3sin
2k
2
a
2
a
R
3
U
1+ka +
1
3
k
2
a
2
−
1+kR +k
2
aR
e
−kR−a
(8.4.2)
Having found the stream function and velocity, the pressure can be found from
equation (8.1.5). Since the pressure satisfies the Laplace equation, it must be associated
with the irrotational portion of the flow: the doublet. Thus, the pressure satisfies
p =−
v
doublet
t
The pressure is thus given by
p = iUA cos/R
2
(8.4.3)
The force needed to produce this motion is found as before by integrating the shear
stresses over the surface of the sphere as in equation (8.2.5). The result is
F
z
=−
0
RR
cos −
R
sin
a
2a
2
sin d
=
4
3
a
3
1
2
+
9
4a
iU +3a
3
1
a
1+
1
a
U
=
4
3
a
3
1
2
+
9
4
2
a
2
dU
dt
+3a
3
2
a
2
1+
2
a
2
U
(8.4.4)
