Graebel W.P. Advanced Fluid Mechanics
Подождите немного. Документ загружается.


184 The Boundary Layer Approximation
Example 6.7.1 Calculation of the separation point on a circular cylinder in a uniform
stream.
Schmidt and Wenner (1941) found experimentally that a good approximation to the
laminar surface flow on a circular cylinder of radius a was given by
U =U
0
2s −0451s
3
−000578s
5
where
s =x/a and x is the distance along the circumference of the cylinder.
Find the predicted separation point using the Stratford and Thwaite criteria.
Solution using Stratford’s criterion. Taking the derivative of U, find that U has a
maximum where 2 −1353s
2
−00289s
4
=0. By the quadratic formula, find that root to
be s
max
= 119765, giving U
max
= 16063U
0
. This is 68.62 degrees from the stagnation
point. Then
s −s
max
2
1−U/U
max
2
−2U
U
2
max
dU
dx
2
−00104 =0
By successively substituting values of s greater than s
max
find the value s =1447, which
corresponds to a separation point at 82.97 degrees from the stagnation point.
Solution using Thwaite’s criterion. Multiplying U to the fifth power and then
carrying out the integration in equation (6.7.1) is tedious, to say the least. Instead
the integration is best carried out numerically using something like the Newton-Cotes
formula. A program for doing this is given in Chapter 10. Separation is predicted at
s =1576, corresponding to an angle of 90.30 degrees from the stagnation point.
These criteria both assume that the separation point does not move in time. In
reality, the region beyond the separation points usually develop vortices and a wake
that contains a vortex street as modeled by von Kármán (Section 3.8). If the flow is
started gradually from rest, the vortices may first align side by side. Soon, however,
they switch to the staggered position, as found in the von Kármán vortex street. As a
vortex grows and is shed, the separation point can move back and forth. As yet, no
simple method is available for predicting this analytically. For the most part, description
of wakes appears to be best done by numerical methods.
Even wakes with minimal large-scale vortices have proven difficult for analytical
methods. In 1930 Goldstein attempted an expansion solution of the wake behind a flat
plate. Some progress was made, but the formidable computations required had to be
done by hand, and progress was small. In two papers in 1968 and 1969, Stewartson
elaborated further on the structure of the flow near the trailing edge of the plate and
found that while Goldstein’s viscous solution held in a very thin layer in the rear of the
body, there was also a thin inviscid layer containing vorticity outside the Goldstein layer
before inviscid irrotational flow was achieved. Complexity thus reigns in wake flow!
6.8 Transformations for Nonsimilar Boundary Layer Solutions
The solutions of the boundary layer equations presented so far are limited to very
special external flows—namely, those outer-velocity profiles given in the Falkner-Skan
problem. Other outer pressure gradients require different methodology and numerical
techniques for their solution. Several transformations have been introduced over the
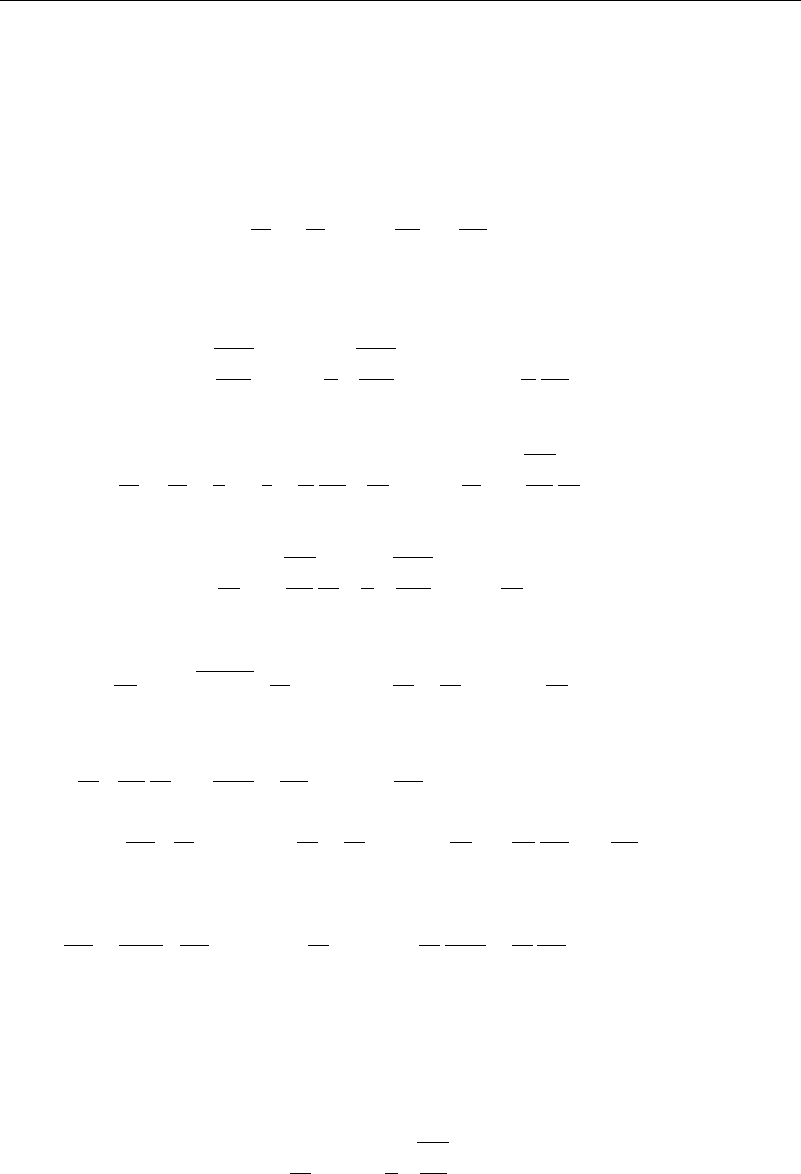
6.8 Transformations for Nonsimilar Boundary Layer Solutions 185
years in attempts to condition the boundary layers to simplify solution methods. These
transformations offer a possible starting point for the utilization of numerical methods.
6.8.1 Falkner Transformation
The transformations used in the solution for flow past a wedge can also be used for
nonsimilar solutions. Start with the steady form of equation (6.2.14)—namely,
u
u
x
+v
u
y
=U
U
x
+
2
u
y
2
(6.8.1)
It is convenient to first suppress as much as is easily possible the growth of the boundary
layer thickness in the x direction. Introduce variables suggested by our Falkner-Skan
solution according to
= x = y
Ux
=
Ux
fx P =
x
U
dU
dx
(6.8.2)
Then, since
=
x
+
2
−
1
x
+
1
U
dU
dx
and
y
=
U
x
it follows that
u =
y
=
U
x
Ux
f
=U
f
(6.8.3)
and
v =−
x
=−
Ux/
1
2x
1+P
f +
f
+
2x
−1+P
f
(6.8.4)
Substituting these into equation (6.8.1), we find, after some arranging, that
U
f
dU
dx
f
+U
2
f
+
U
2x
−1+P
2
f
2
−U
2
2
f
2
1
2x
1+P
f +
f
+
2x
−1+P
f
=
U
2
x
3
f
3
+U
dU
dx
Multiplying the above equation by x/U
2
and simplifying, the result is
3
f
3
+
1+P
2
f
2
f
2
+P
1−
f
2
=
f
2
f
−
f
2
f
2
(6.8.5)
The left-hand side of the equation is essentially the equation seen in the similarity
solution, except now P can depend on x. Since a stream function is the starting point,
continuity is automatically satisfied.
It is seen that equation (6.8.5) is a third-order partial differential equation. In
numerical solutions, it is somewhat easier to deal with first-order partial differential
equations. To get to that point here, make the change of variables
F =
f
V=
U
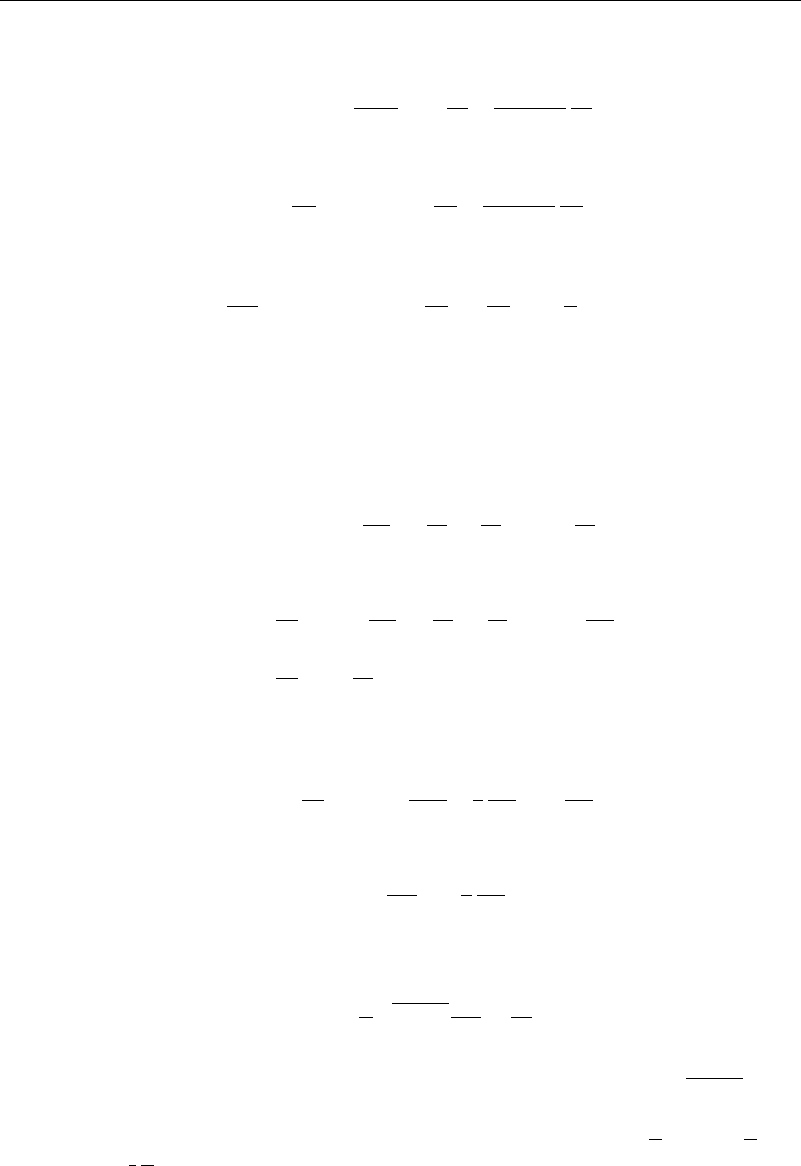
186 The Boundary Layer Approximation
where F is then the dimensionless u velocity component, and V is a scaled dimensionless
version of the v velocity component. Then equation (6.8.3) becomes
V =−
1+P
2
f +
f
+
P −1
2
f
Differentiating this with respect to gives
V
=−
PF +
F
+
P −1
2
F
(6.8.6)
The momentum equation (6.8.4) can now be written as
2
F
2
=−P +F
PF +
F
+
F
V +
2
P −1F
(6.8.7)
6.8.2 von Mises Transformation
Von Mises (1927) suggested the transformation =U
2
−u
2
and used as the dependent
variable and x and as the independent variables. Then
d =−vdx +udy (6.8.8)
d =2
U
dU
dx
−u
u
y
−v
u
x
dx −2
u
y
d (6.8.9)
It is seen from this that
x
=2
U
dU
dx
−u
u
y
−v
u
x
=−2
2
u
y
2
(6.8.10)
=−2
u
y
d (6.8.11)
where the term on the far right of equation (6.8.10) comes from the momentum equation.
Taking further differentials gives
d
=−2
2
u
xy
+
v
u
2
u
y
2
−2
2
u
y
2
d
From this it follows that
2
2
=−
2
u
2
u
y
2
(6.8.12)
Combining equations (6.8.10) and (6.8.12) gives the final form of the transformed
equation as
U
2
−
2
2
=
x
(6.8.13)
This is to be solved subject to the conditions =U
2
at = 0 =0at =.
Once equation (6.8.13) is integrated, u can be found from u =
U
2
−. Since
dy = d +udx/u y is found from y =
0
d/u, the integration being performed on a
line of constant x. The v velocity component is found from v =
0
v
y
dy =−
u
x
dy =
−
1
u
u
x
d on a line of constant x. Since there is a singularity in the integrand at the
wall, care must be used in carrying out the integration.

6.8 Transformations for Nonsimilar Boundary Layer Solutions 187
6.8.3 Combined Mises-Falkner Transformation
The previous two transformations can be combined into one step by the following:
=
1
U
x
Uds =f
U
/
m
u=U
√
w (6.8.14)
At this point m is a constant and f is a function, both to be chosen. For convenience,
note that
x
=
U
U
y
=0
x
=
f
f
−
m
y
=
mu
x
=
U
U
+
1
f
f
−
mv
y
=
mu
Using these in the boundary layer equation yields
w
=
2
U
dU
d
1−w −
f
df
d
w
+m
2
2−2/m
f
2/m
√
w
2
w
2
+
1−1/m
w
(6.8.15)
There are two choices for m and f that have proven to be useful in the past.
1. m = 1/2f=
−1/4
. In this case equation (6.8.15) reduces to
w
=
2
U
dU
d
1−w −
4
w
+
√
w
4
2
2
w
2
−
1
w
(6.8.16)
2. m = 1f=1. In this case equation (6.8.15) reduces to
w
=
2
U
dU
d
1−w +
√
w
2
w
2
(6.8.17)
Integration in both cases proceeds as in the previous two cases.
6.8.4 Crocco’s Transformation
Crocco’s transformation (1939) is unusual in that it uses shear stress rather than a
velocity function as a dependent variable. Letting =
u
y
, since
du =
u
x
dx +
u
y
dy =
u
x
dx +
dy then
dy =
du −
u
x
dx
Also
d =
x
dx +
y
dy =
x
−
u
x
y
dx +
y
du so that
x
=
x
−
u
x
y
u
=
y
Then
d
u
=
x
1
y
dx +
y
1
y
du −
u
x
dx
so that
2
u
2
=
2
2
2
y
2
−
1
y
2
Similarly
2
y
2
=
u
x
+v
y

188 The Boundary Layer Approximation
With further algebra, the preceding can finally be reduced to
2
u
2
+
u
x
1
+U
dU
dx
u
1
=0 (6.8.18)
The accompanying boundary conditions are /u = 0atu = 0 and =0atu =U .
In using any of the previous transformations it is necessary to first decide whether
the dependent variable is the one best suited to the method. The Falkner transformation
results in an equation for x, the von Mises an equation for essentially uy,
the combined method an equation for u, and Crocco’s method for an equation for
xu. The equations are of about the same order of complexity, and all require a guess
of either the dependent variable or its derivative on the wall. The choice of method to
be used then depends on the end result sought and the suitability of the method to the
boundary conditions.
6.8.5 Mangler’s Transformation for Bodies of Revolution
Mangler’s transformation differs in intent from the four previous transformations in that
its purpose is to change an axisymmetric flow problem into a two-dimensional flow
problem rather than to condition the equations.
Consider the flow on a body generated by revolving the curve y = rx about the
x-axis. Providing the body radius r is much greater than the boundary layer thickness,
the boundary layer equations are
u
u
x
+v
u
y
=U
dU
dx
+
2
u
y
2
ru
x
+
rv
y
=0
Using the transformation x
=
x
0
r
2
dx y
= ry, then u
= u v
=
1
r
v +
yu
r
dr
dx
, so that
u =u
v=−
yu
r
dr
dx
+rv
, then
u
u
x
+v
u
y
=U
dU
dx
+
2
u
y
2
u
x
+
v
y
=0
(6.8.19)
Thus, any solution procedure suited to two-dimensional boundary layer problems can
readily be transferred to flow past axisymmetric bodies.
6.9 Boundary Layers in Rotating Flows
The flows previously studied are caused by either pressure gradients, body forces, or
moving boundaries. In these cases, the resulting flow is in the direction of the gradient,
or body force, or boundary motion. In the atmosphere, however, as is apparent from
weather maps that show isobars, the flow tends to be along the isobars, due to Earth’s
rotation.
Studying flow on a sphere is difficult, so to simplify matters, adopt the viewpoint
of the meteorologists and oceanographers and use the beta plane approach. That is,
look at a relatively small segment of Earth—say, a square region 1,000 kilometers on a
side—and consider that portion of Earth to be flat, rotating at the rate
0
sin , where
is the latitude of the center of the region and
0
is Earth’s rotation speed of 2
radians per day. Introducing this into equation (1.17.4), the principal term of interest
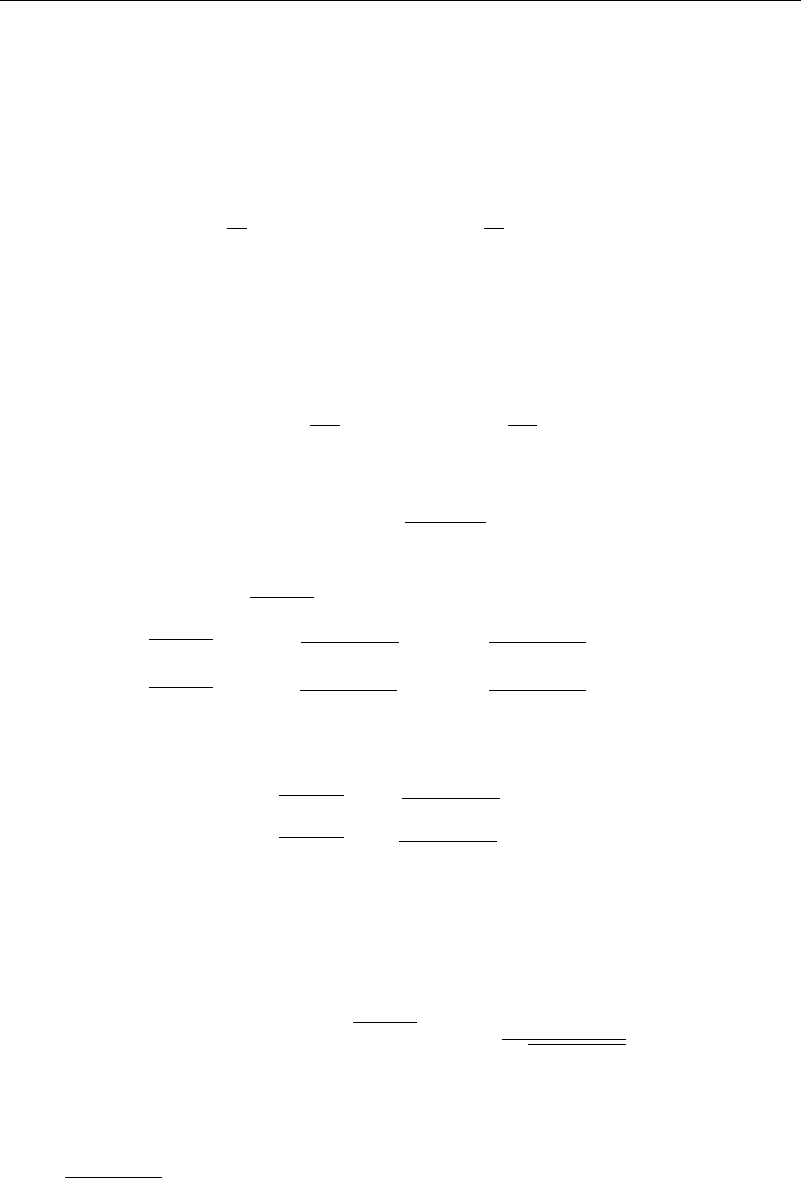
6.9 Boundary Layers in Rotating Flows 189
is the Coriolis acceleration term 2
0
sin ×v, where the angular velocity vector is
perpendicular to Earth’s surface, and the velocity vector is in plane of the tangent to
the Earth’s surface. The neglect of the centripetal acceleration is justified, since it adds
essentially a small body force, and the remaining terms are considered small compared
to the Coriolis terms.
If the vertical velocity component is neglected, the simplified Navier-Stokes equa-
tions, first presented by Ekman (1905), are then
−2v
0
sin =−
p
x
+
2
u 2u
0
sin =−
p
y
+
2
v (6.9.1)
When viscosity is neglected, it is seen that the flow is along the lines of constant
pressure.
Ekman considered the problem where the wind shear at the surface of the ocean
was in the x direction, no pressure gradients were present, and the velocity components
only depended on the vertical coordinate. Then equations (6.9.1) reduce to
−2v
0
sin =
d
2
u
dz
2
2u
0
sin =
d
2
v
dz
2
(6.9.2)
Multiplying the second equation by i and adding it to the first gives
2iu +iv
0
sin =
d
2
u +iv
dz
2
With z negative downward, this has the simple solution with
u +iv = U +iVe
1+iz
√
0
sin /
or
u =e
z
√
0
sin /
U cos z
0
sin / −V sin z
0
sin /
(6.9.3)
v = e
z
√
0
sin /
V cos z
0
sin / +U sin z
0
sin /
In particular, if the wind shear is such that the surface water is in the x direction, then
V = 0 and
u =Ue
z
√
0
sin /
cosz
0
sin /
v = Ue
z
√
0
sin /
sin z
0
sin /
(6.9.4)
It is seen from equations (6.9.4) that the path of the tip of the velocity vector traces
a spiral as we move down from the free surface. In the northern hemisphere it starts
pointing eastward, say, then turns north, then west, then southward, and repeating the
process and decreasing in magnitude as we proceed downward. Computing the discharge
by integrating the first of equations (6.9.3), find that
Q
x
+iQ
y
=
−
0
u +ivdz =U
−
0
e
√
0
sin /1+iz
dz =
U1−i
2
0
sin /
(6.9.5)
Thus, equal quantities of fluid are transported perpendicular to the wind shear stress as
in the direction of the wind stress.
Boundary layers associated with rotating flows are referred to as Ekman
layers. From equations (6.9.4) we see that the thickness of the layer is of the
order
/
0
sin .

190 The Boundary Layer Approximation
Another example of rotating boundary layers that does not necessarily need Earth-
magnitude dimensions is for a fluid in weak rotation above a stationary plate. A stirred
cup of tea with a few loose tea leaves would be an example of such a flow. In this case
there is a radial pressure gradient p/r =r
2
outside of the boundary layer. Taking
radial and circumferential velocity components in the form u = rfz v = rhz,
the equations are
−2rh
2
−r
2
=r
d
2
f
dz
2
2rf
2
=r
d
2
h
dz
2
(6.9.6)
Again, multiplying the second of equations (6.9.6) by i and adding it to the first, the
result is
2if +ih −
=
d
2
f +ih
dz
2
With z =0 at the bottom of the cup, the solution is
d
2
f +ih
dz
2
−2if +ih =−
therefore,
f +ih =−i
1−e
−1+iz
√
/
=−i
1−e
−z
√
/
cosz
/ −i sin z
/
Splitting into real and imaginary parts gives
h =−1+e
−z
√
/
cosz
/
f =e
−z
√
/
sin z
/
(6.9.7)
Above the boundary layer the almost neutrally buoyant tea leaves move in concentric
circles, the centripetal force balanced by the pressure gradient. As they move into the
boundary layer, the centripetal force diminishes, while the pressure gradient remains
unchanged, pushing the tea leaves to the center of the cup.
There is a popular belief that when draining a bathtub the water swirls one way in
the northern hemisphere and the opposite way in the southern hemisphere. Since Earth’s
rotation is small, its effects are mostly felt when lengths of hundreds of kilometers are
involved. For something like a bathtub, the length scale is so small that the Coriolis
acceleration is negligible. The behavior instead depends strongly on what swirl was
introduced when the tub was filled and on the geometry of the tub. Experiments with
well-designed circular containers with carefully centered outlets show that it is necessary
to wait many hours—perhaps even an entire day—for initial effects to die out. After
that, the swirl is hardly noticeable until the depth is of the order of the Ekman layer.
When that happens, the direction of swirl reverses several times as the layer becomes
thinner and thinner.
Problems—Chapter 6 191
Problems—Chapter 6
6.1 The similarity solution for flow into a sink between two inclined plates can be
obtained from the Falkner-Skan equations by putting
=
dU
dx
=0=
2
dU
dx
=1 x = y/ =
x/
giving the equation
f
+1 −
f
2
=0f0 =f
0 = 0f
→1as →
Show that this equation may be integrated to give
f
=3 tanh
2
√
2
+1146
−2
where the prime denotes differentiation with respect to r.
6.2 The equation for source flow between inclined plates f
+f
2
+4f +4a = 0
can be linearized if in some sense f can be considered to be small. In that case, the
equation becomes f
+4f +4a ≈ 0. Solve this equation subject to f vanishing at
1
and at
2
.
6.3 Find the similarity solution for a two-dimensional submerged jet emitting at the
origin. Show that the form x y = =
f = y
M/
2
x
2
1/3
, reduces the
Navier-Stokes equations to a third-order ordinary differential equation. This equation
can be integrated twice, reducing it to w first-order differential equation.
6.4 The following form has been suggested for flow in the wake of a flat plate:
x y =
2
x
2
/
2
1/3
f =y
/x
1/3
with U =
√
3C
2
x
1/3
. Here, represents the constant vorticity at the edge of the
boundary layer, and C is also a constant. Show that this is a suitable similarity solution
of the boundary layer equations. Do not attempt to solve the equation.
6.5 The boundary layer equations place severe restrictions on the possibility of
having a similarity solution. To make a general search for similarity solutions, start with
the form x y =
ex +gxf
=
y
hx
, and substitute it into the boundary
layer equations. Find the restrictions that must be placed on ex gx, and hx to
obtain a differential equation solely in terms of f and .
6.6 Show that a solution of the boundary layer equation (in fact, the full Navier-
Stokes equation) can be found for an infinite flat plate in a uniform stream (speed U )
with constant suction at the wall. The suction induces a downward velocity of strength
V
0
. Such suctions have been used as a method for controlling boundary layer separation.
Use a velocity form of the type vy=u y V.
6.7 Fluid enters a channel of width 2b at a uniform speed U
0
. Because of the
no-slip condition, the wall shear changes gradually from the uniform flow to the standard
Poiseuille parabolic flow. The flow will consist of two wall boundary layers plus an
inner core where the speed changes with x but is uniform across its domain. Since the
flow can be expected to be symmetric with respect to the centerline, choose y as the
distance measured from the bottom wall.

192 The Boundary Layer Approximation
Using the profile v
x
=
U2 −
2
0 ≤ ≤ 1
U 1 ≤ ≤ hx/ =y/
with U being the speed outside of the boundary layer, find U and the distance needed
to establish the flow.
6.8 The potential flow against an infinite plate is described by the velocity potential
= Ax
2
−y
2
, the plate being at y = 0. Using a parabolic velocity profile, solve for
the boundary layer thickness and wall shear.
6.9 The form u =
UA +B cosC 0 ≤ ≤ 1
U > 1=
y
is proposed as an approximation for the velocity profile in a boundary layer. Find
appropriate choices for A B, and C, and calculate the displacement and momentum
thicknesses.
6.10 A thin viscous layer of liquid flows down a vertical wall under the force of
gravity. The flow at the outer edge of the layer has the speed U =
√
2gx. Assuming the
layer in the liquid to be of the form v
x
=
U2 −
2
0 ≤ ≤ 1
U 1 ≤ ≤ hx/ =y/
find hx and x.
6.11 Viscosity does play a small role in the damping of free surface gravity waves.
A simple model for computing this is to say
d
dt
KE +PE
=−, where is the
dissipation function discussed in Chapter 1. For the two-dimensional traveling wave
given by x z t = cA sin kx −cte
kz
x t =A cos kx −ct
i
c=
√
g/k, compute
the potential and kinetic energies and the dissipation function to find the rate of decay
of the wave. Assume A depends exponentially on time.
6.12 The profile U = U
0
1−
x
L
has been used to study separated flows. Calculate
the location of the separation point using both the Thwaites and Stratford criteria.

Chapter 7
Thermal Effects
7.1 Thermal Boundary Layers 193
7.2 Forced Convection on a Horizontal
Flat Plate 195
7.2.1 Falkner-Skan Wedge Thermal
Boundary Layer 195
7.2.2 Isothermal Flat Plate 195
7.2.3 Flat Plate with Constant
Heat Flux 196
7.3 The Integral Method for Thermal
Convection 197
7.3.1 Flat Plate with a Constant
Temperature Region 198
7.3.2 Flat Plate with a Constant
Heat Flux 199
7.4 Heat Transfer Near the Stagnation
Point of an Isothermal Cylinder 200
7.5 Natural Convection on an
Isothermal Vertical Plate 201
7.6 Natural Convection on a Vertical
Plate with Uniform Heat Flux 202
7.7 Thermal Boundary Layer on
Inclined Flat Plates 203
7.8 Integral Method for Natural
Convection on an Isothermal
Vertical Plate 203
7.9 Temperature Distribution in an
Axisymmetric Jet 204
Problems—Chapter 7 205
7.1 Thermal Boundary Layers
If temperature gradients exist in a flow, the momentum boundary layer for large Reynolds
numbers discussed in Chapter 6 can be accompanied by a thermal boundary layer. Recall
equation (1.14.7), where it was found from the first law of thermodynamics that
Du
Dt
=− ·q +
dr
dt
+ (1.14.7)
Taking u = c
p
T and q =−kT for the internal energy and heat flux, and considering
only cases where there is no internal heat generation and dissipation and compressibility
effects are secondary, this becomes
c
p
DT
Dt
=k
2
T (7.1.1)
Here, c
p
is the heat capacity at constant pressure J/kg ·K, and k is the thermal
conductivity W/m ·K.
193
