Грачева М.В. и др. Моделирование экономических процессов

Подождите немного. Документ загружается.

Y(t),I(t)f

C(0) e*

7(0)

-C(0)

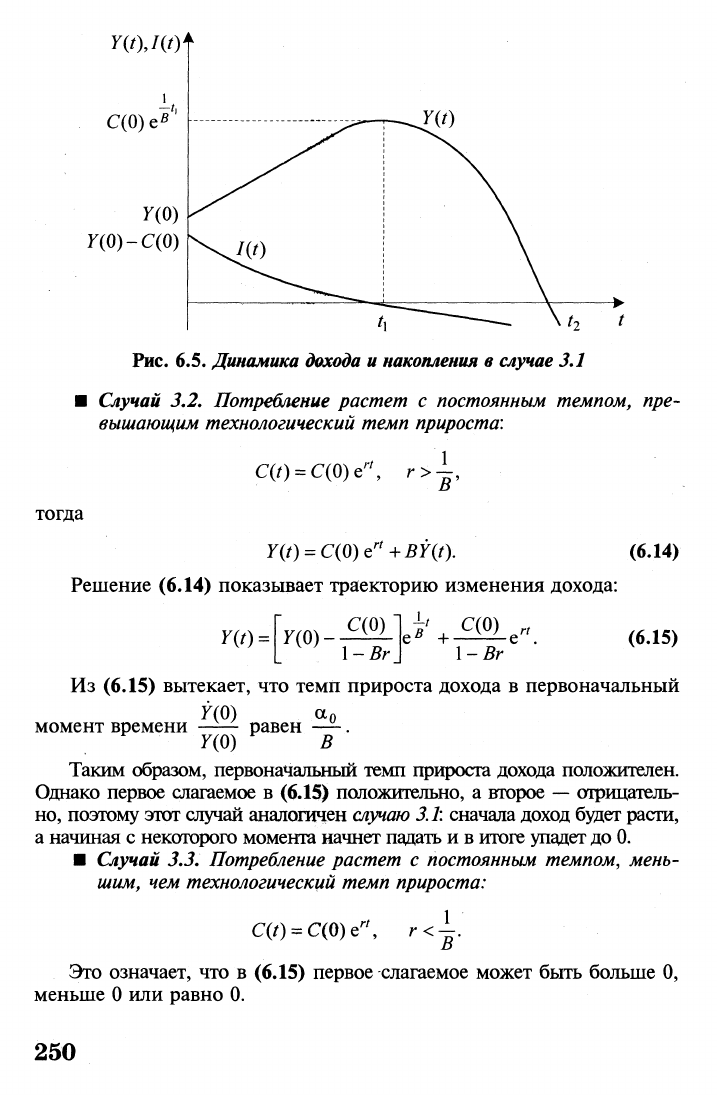
Рис. 6.5.

Динамика дохода

накопления

случае

3.1

Случай

3.2.

Потребление растет

постоянным

темпом,

пре-

вышающим технологический темп

прироста:

C(f) = C(0)e'\

г >

В'

тогда

Y(t) = C(0)e

'+BY(t). (6.14)

Решение (6.14) показывает траекторию изменения дохода:

Y(t) =

7(0)-

С(0)

1-5г

\-Вг

(6.15)

Из (6.15) вытекает, что темп прироста дохода в первоначальный

7(0) а

момент времени —-— равен —^.

7(0) В

Таким образом, первоначальный темп прироста дохода положителен.

Однако первое слагаемое в (6.15) положительно, а второе

—

отрицатель-

но,

поэтому этот случай аналогичен

случаю

3.1:

сначала доход будет расти,

а начиная с некоторого момента начнет падать и в итоге упадет

до

•

Случай

3.3.

Потребление растет

постоянным

темпом,

мень-

шим,

чем технологический

темп

прироста:

С(/) = С(0)е

Это означает, что в (6.15) первое слагаемое может быть больше 0,

меньше 0 или равно 0.

250

Случай

3.3.1.

Темп

прироста потребления меньше первоначального

темпа прироста

дохода.

Пустьв(6.15) 7(0)--^-> 0, тогда (1-Вг)>^-,

\-Вг 7(0)

следовательно,

r<S±.

Таким образом, если темп роста потребления меньше темпа

прироста дохода в первоначальный момент времени г<—^

то в (6.15) оба слагаемых положительны и доход неограниченно

растет во времени.

При /->

оо

а(/) -» 1, р(/) -> 0, т.е. в предельном случае норма

накопления равна 1, а потребления 0. Такой тип развития («накоп-

ление ради накопления») может быть целесообразным только на

ограниченном отрезке времени.

Случай 3.3.2.

Потребление

растет с

постоянным

темпом, мень-

а ^-t

шим

технологического темпа прироста

и равным —^-; C(t)

С(0)

тогда из (6.15):

ГЮ-Г^-е^; ^

Ро=1-«

i-a

Следовательно, -^-

7(0) и Y(t)

7(0) е~*',

1-<х

/(/) У(0)е* -С(0)е*

Л а

7(0) е*

Другими словами, в этом случае норма накопления постоянна, а

темп прироста национального дохода прямо пропорционален этой

норме накопления и обратно пропорционален приростной капита-

лоемкости.

Случай 3.3.3. Темп

прироста потребления больше первоначального

темпа прироста

дохода:

—

< —

Из (6.15) вытекает, что в этом случае доход в некоторый мо-

мент перестанет расти и затем уменьшится до нуля.

251

Таким образом, модель Харрода—Домара указывает на

случай

3.3.2

как на наиболее разумный вариант экономического развития. При

этом варианте потребление и накопление растут с постоянным

темпом, причем темп прироста национального дохода также по-

стоянен и равен —-.

Из модели Харрода—Домара следует, что постоянного сба-

лансированного роста можно достичь двумя путями: либо в на-

чальный момент выбирается норма накопления ао, и тогда ищут

оптимальный темп роста потребления г, который будет равен

—; либо выбирается желаемый темп роста потребления г и то-

гда норма накопления, при которой можно достичь такого темпа,

равняется —-.

Интересно, что в этом случае потребление и доход в долгосроч-

ном периоде растут с одинаковым темпом — и потребление со-

ставляет постоянную часть от дохода, т.е. функция потребления

совпадает с функцией Кейнса в долгосрочном периоде, когда сред-

няя склонность к потреблению не меняется.

С помощью модели Харрода—Домара среди возможных вариан-

тов развития определяется наиболее предпочтительный, однако она

не объясняет детерминант экономического роста. Эти детерминан-

ты подробно анализируются в модели Солоу.

6.2.2. Модель Солоу

Модель экономического роста Солоу является необходимой от-

правной точкой практически всех исследований экономического

роста. С ее помощью выявляются причины временного и постоян-

ного устойчивого роста экономики и существование межстрановых

различий в уровне жизни населения.

В модели рассматриваются четыре переменные: Y

—

выпуск; К

—

капитал; L — труд и Е

—

эффективность труда одного работника,

зависящая от состояния его здоровья, образования и квалифика-

ции. Переменная Е отражает уровень «знаний», накопленных в об-

ществе, или трудосберегающий тип научно-технического прогресса,

под влиянием которого повышается эффективность труда одного

работника.

Выпуск Y может изменяться во времени только при изменении

во времени факторов производства: К, L, Е. Изменение численно-

сти работников и эффективности труда Е всегда рассматриваются

252

совместно: в каждый момент времени в экономике насчитывается L

работников с возросшей эффективностью труда или возросшее чис-

ло работников с постоянной (начальной) эффективностью труда

(£Е).

Таким образом, выпуск описывается производственной

функцией Y

F(K, LE).

Относительно производственной функции предполагается:

1) несущественность влияния других факторов производства, в

частности, земли и природных ресурсов;

2) постоянная отдача от масштаба. Экономически такая предпо-

сылка соответствует достаточно большой экономике, для которой

выигрыш от специализации уже исчерпал себя, и поэтому новые

факторы производства используются тем же технологическим спо-

собом, что и уже существующие.

Последнее предположение позволяет перейти к производствен-

ной функции в интенсивной форме

—

в расчете на единицу труда с

постоянной эффективностью:

X = F(-£-, l)

-±-F(K,LE).

LE KLE ) LE

Обозначим k

^- — уровень капиталовооруженности одного

работника с постоянной эффективностью труда; у--

— — произ-

водительность труда одного работника с постоянной эффективно-

стью труда. Получим зависимость производительности труда от

уровня капиталовооруженности у =

f(k).

Таким образом, выпуск в расчете на единицу труда с постоян-

ной эффективностью зависит только от уровня капиталовооружен-

ности и не зависит от масштаба экономики

;

f'(k)>0;

f\k)<0;

Д0)

Наиболее часто используется конкретный пример производст-

венной функции, обладающей перечисленными свойствами, —

производственная функция Кобба—Дугласа

F(K,LE)

(LE)

;

0 <

Описание модели

Основными предпосылками модели Солоу являются сле-

дующие:

Поэтому можно вместо анализа экономики в целом, исследовать единичную

экономику, обладающую одной единицей труда с постоянной эффективностью

и "ттт единицами капитала.

253

Выпуск в экономике расходуется на потребление и инвести-

ции, государство отсутствует, экономика закрытая, так что основ-

ное тождество национальных счетов имеет вид: у

—

с + /, где с, /

—

соответственно потребление и инвестиции на единицу труда с не-

изменной эффективностью.

Все, что сберегается, инвестируется, т.е. инвестиции равны сбе-

режениям. Одна единица инвестиций превращается без дополнительных

издержек в одну единицу нового капитала. Лаг отсутствует. Сбережения

пропорциональны доходу. Норма сбережения s задается экзогенно и по-

стоянна во времени

(0 <

1). Таким образом, / =

sfljc).

Понятия «население» и «рабочая сила» совпадают.

Существующий капитал изнашивается с нормой 8 в год. Тогда

изменение запасов капитала АК определяется разностью общей вели-

чины инвестиций sYn износа капитала

ЗК

т.е.

АК=

K(t) =sY

—

ЪК.

В расчете на единицу труда с постоянной эффективностью уро-

вень капиталовооруженности изменится на

Ak(t) - k(t) =

(

К(0

)

k{t)ЦОт

~*('> Д0£(0-K(t)L{t)L(t)

dt{L(t)E(t)) (L(t)E(t)f

sY(t)-bK(t)

f/4

Z(0 ,,\E(t) ^

/7/чч

, -

ч|/ч

1(0 E(t)

где п -

——- —

темп роста численности населения; g

—~- — темп

L{t) E(t)

роста технологического прогресса.

Таким образом,

Ak(t) s k(i) = sf(k(t)) -

(л +

8)k(t).

(6.16)

Соотношение (6.16) является в модели ключевым. Оно утверждает,

что величина изменения уровня капиталовооруженности одного работ-

ника с постоянной эффективностью труда определяется соотношением

двух величин в расчете на одного работника

—

инвестиций sf(k(t)), фак-

тически произведенных в экономике, и величины инвестиций, необхо-

димых для того, чтобы сохранять достигнутый уровень к в условиях рос-

та населения с темпом п, роста эффективности труда с темпом g и вы-

бытием капитала с нормой б (вычитаемое в правой части (6.16)).

Таким образом, в экономике уровень капиталовооруженности к

падает, если фактические инвестиции меньше, чем необходимые

для сохранения уровня к, и возрастает, если

s(J{k)) >

(п + g + 8)k.

Вводится понятие устойчивого уровня

к*,

при котором величины

фактических и необходимых инвестиций совпадают (рис. 6.6),

254

т.е.

к -

О,

откуда

sAk*) =(n+g + S)k*

f(k);sf(k) f

f(k')

sf(k)

Рис.

6.6.

Устойчивое состояние

модели Солоу

В устойчивом состоянии

к*

неизменно, производительность тру-

да работника с постоянной эффективностью постоянна: у =

j{k*).

Общий объем производства Y = y(LE) растет с темпом (п + g), a

производительность труда

— =

уЕ растет с темпом g, так же, как и

уровень капиталовооружености труда —

К к (L-E)

к-Е.

Более подробная характеристика устойчивого состояния эконо-

мики приведена в табл. 6.1.

Рост производительности труда в устойчивом состоянии определяется

исключительно темпом роста технологического прогресса (см. табл. 6.1).

В отсутствие технологического прогресса (т.е. при неизменной

эффективности труда) для экономики с растущим населением в устой-

чивом состоянии уровень капиталовооруженности остается постоян-

ным, производительность труда не меняется, общий вьшуск и общий

запас капитала растут с темпом, равным темпу роста населения п.

Если же отсутствуют и рост населения и технологический про-

гресс, то в устойчивом состоянии при постоянном уровне капита-

ловооруженности производительность труда, общий выпуск и об-

щий запас капитала остаются неизменными.

Таким образом, причинами, определяющими рост общего вы-

пуска и общего запаса капитала в устойчивом состоянии, являются

увеличение численности населения и технологический прогресс, а

устойчивый рост производительности труда и капиталовооруженно-

сти достигается только при наличии технологического прогресса.

255

Таблица 6.1

Темпы роста показателей

устойчивом состоянии экономики

Показатель

1 Капиталовооружен-

ность работника с

постоянной эффек-

тивностью к =

Капиталовооружен-

ность работника

= кЕ

Общий запас капита-

ла К = k(LE)

Произюдительность

труда одного работ-

ника с постоянной

эффективностью

Производительность

труда одного работ-

ника

—

= уЕ

Общий выпуск Y =

При

НТП

и росте

населения

(АЕ AL }

hr=*-r=-J

п +g

отсутствие

НТП

при росте

населения

(АЕ AL )

—

отсутствие

НТП

и роста

населения

(¥•« Н

—

Изменение численности населения влияет на величину устой-

чивого уровня капиталовооруженности, но не влияет на темпы рос-

та производительности труда и капиталовооруженности в устойчи-

вом состоянии.

Влияние изменения нормы сбережения

Предположим, что экономика находится в устойчивом состоя-

нии: с устойчивым уровнем капиталовооруженности

к*

и соответст-

вующей нормой сбережения s\. Пусть под влиянием внешних изме-

256

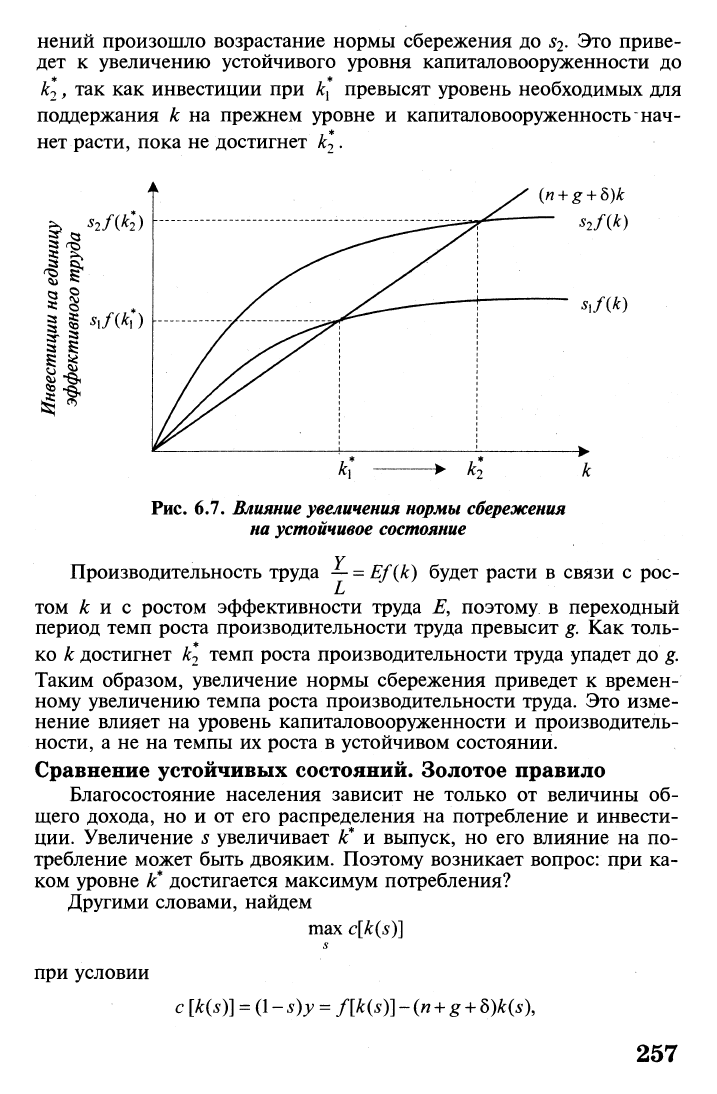
нений произошло возрастание нормы сбережения до ^. Это приве-

дет к увеличению устойчивого уровня капиталовооруженности до

к*

так как инвестиции при к* превысят уровень необходимых для

поддержания к на прежнем уровне и капиталовооруженность нач-

нет расти, пока не достигнет к\.

2$ г§

f{k

)

ас

sx№)

{n +

b)k

f(k)

sif(k)

Рис. 6.7.

Влияние увеличения нормы сбережения

на устойчивое состояние

Производительность труда

— =

Ef(k) будет расти в связи с рос-

том к и с ростом эффективности труда Е, поэтому в переходный

период темп роста производительности труда превысит g. Как толь-

ко к достигнет

к*

темп роста производительности труда упадет до g.

Таким образом, увеличение нормы сбережения приведет к времен-

ному увеличению темпа роста производительности труда. Это изме-

нение влияет на уровень капиталовооруженности и производитель-

ности, а не на темпы их роста в устойчивом состоянии.

Сравнение устойчивых состояний. Золотое правило

Благосостояние населения зависит не только от величины об-

щего дохода, но и от его распределения на потребление и инвести-

ции. Увеличение s увеличивает

к*

и выпуск, но его влияние на по-

требление может быть двояким. Поэтому возникает вопрос: при ка-

ком уровне

к*

достигается максимум потребления?

Другими словами, найдем

max с[А:(»]

при условии

[*(*)]

- s)y = f[k(s)] - (п + g + 8Ж*),

257

отсюда

дс

дк

=\f'(k)-(»

+ 8)]

OS OS

Возрастание s увеличивает к. Влияние же на величину потребления

зависит от того, превысит ли предельная производительность капитала

/'(к) величину (п + g +

5).

Увеличение уровня капиталовооруженности на

единицу увеличивает величину инвестиций, необходимых для

того,

чтобы

капиталовооруженность сохранилась на новом, более высоком уровне, на

(п + g +

5).

Если предельная производительность капитала меньше вели-

чины (п

g + 5), то прирост общего выпуска недостаточен для поддер-

жания к на новом устойчивом уровне и, следовательно, потребление

должно упасть, хотя экономика достигнет нового устойчивого состояния.

Если же предельная производительность капитала больше, чем

(п + g + 5), то прирост общего выпуска превышает объем необходимых

инвестиций, так что увеличиваются и инвестиции, и потребление. Если

же

f'(k) = (п + g + 5), то это означает, что достигается максимально воз-

можное потребление из всех возможных устойчивых состояний и не-

большое изменение в уровне капиталовооруженности к никак не повлия-

ет на величину потребления. Устойчивый уровень капиталовооруженно-

сти,

при котором достигается максимально возможное потребление, на-

зывается

уровнем,

соответствующим Золотому правилу накопления. Золо-

тое правило накопления

состоит в выборе нормы сбережений s, обеспечи-

вающей достижение именно этого устойчивого состояния.

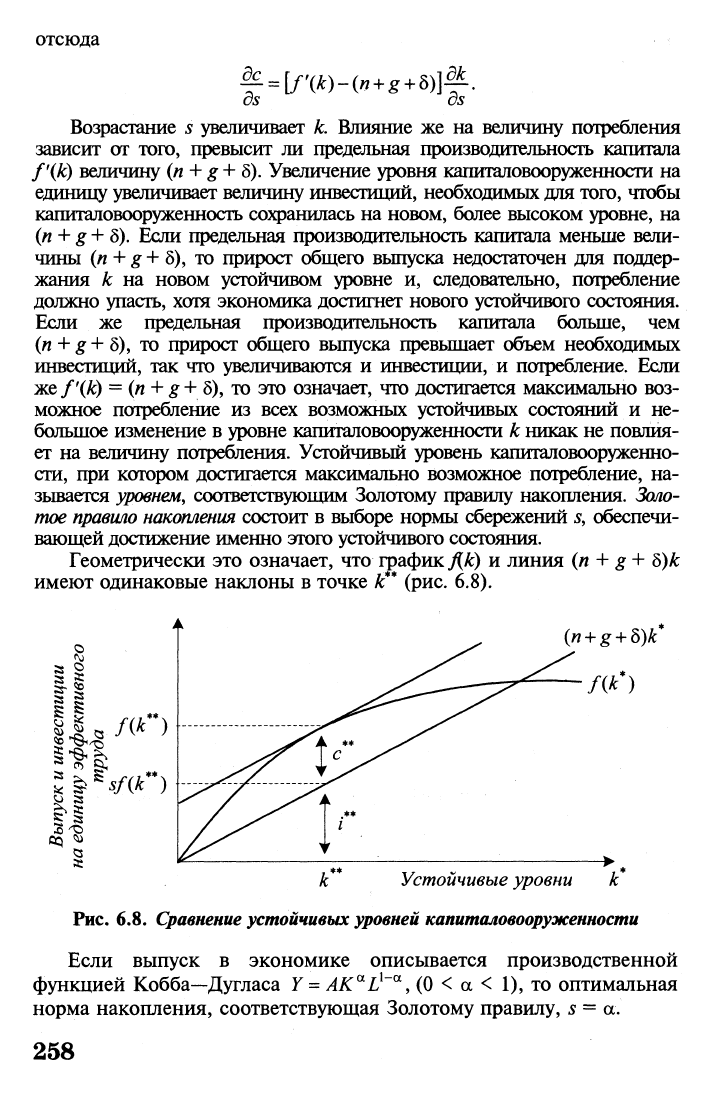
Геометрически это означает, что график ДА:) и линия (п + g + 3)k

имеют одинаковые наклоны в точке

к**

(рис. 6.8).

Устойчивые уровни

Рис.

6.8.

Сравнение устойчивых уровней капиталовооруженности

Если выпуск в экономике описывается производственной

функцией Кобба—Дугласа Y - AK

, (0 < а < 1), то оптимальная

норма накопления, соответствующая Золотому правилу, s = а.

258

Переход к устойчивому состоянию,

соответствующему Золотому правилу

Возникает вопрос о развитии экономики, которая осуществляет

переход от первоначального устойчивого состояния, не соответст-

вующего Золотому правилу, к устойчивому состоянию с макси-

мально возможным потреблением.

Случай 1. Первоначальный устойчивый уровень капиталово-

оруженности превышает уровень, соответствующий Золотому правилу

В этом случае проводится политика, направленная на снижение

нормы сбережения до уровня, соответствующего Золотому правилу.

Пусть происходит одномоментное снижение нормы сбережения. В

этот момент резко вырастет потребление с, а инвестиции / упадут.

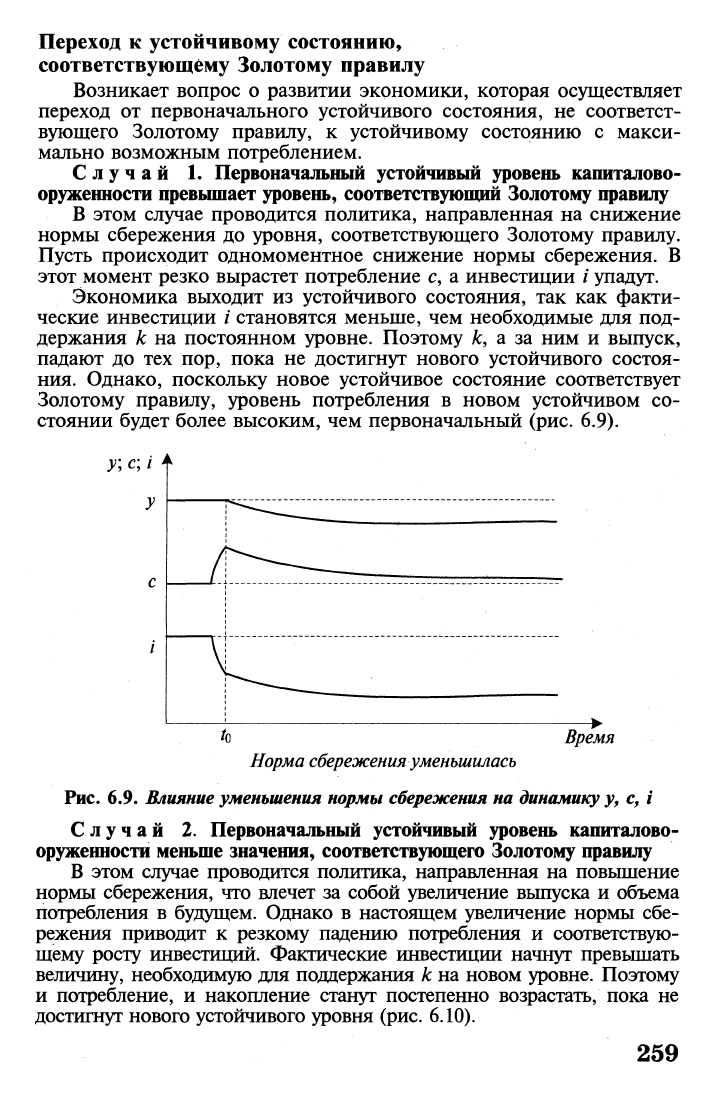
Экономика выходит из устойчивого состояния, так как факти-

ческие инвестиции / становятся меньше, чем необходимые для под-

держания к на постоянном уровне. Поэтому fc, а за ним и выпуск,

падают до тех пор, пока не достигнут нового устойчивого состоя-

ния. Однако, поскольку новое устойчивое состояние соответствует

Золотому правилу, уровень потребления в новом устойчивом со-

стоянии будет более высоким, чем первоначальный (рис. 6.9).

Время

Норма сбережения уменьшилась

Рис. 6.9.

Влияние уменьшения нормы сбережения на динамику

у, с, i

Случай 2. Первоначальный устойчивый уровень капиталово-

оруженности меньше значения, соответствующего Золотому правилу

В этом случае проводится политика, направленная на повышение

нормы сбережения, что влечет за собой увеличение выпуска и объема

потребления в будущем. Однако в настоящем увеличение нормы сбе-

режения приводит к резкому падению потребления и соответствую-

щему росту инвестиций. Фактические инвестиции начнут превышать

величину, необходимую для поддержания к на новом уровне. Поэтому

и потребление, и накопление станут постепенно возрастать, пока не

достигнут нового устойчивого уровня (рис. 6.10).

259