Грачева М.В. и др. Моделирование экономических процессов

Подождите немного. Документ загружается.

?2*

а-с

2(«-с)

лш

ъъ

а-с

2Ъ

2(а-сУ

5Ъ -

я-с

(

~~4Ъ~

^^2\\

а-с

1-Ъ

а-

1 Л i \ ^»

i i \ i \

i i \1 Л

4 4 \

-_с_

2{а-с)а-

^4*

(<7l)

^^(^гЧ^

-_£ 2(а-с) £Lz£

Ч\

АЪ

ЪЪ

5Ъ

2Ъ

ЪЪ

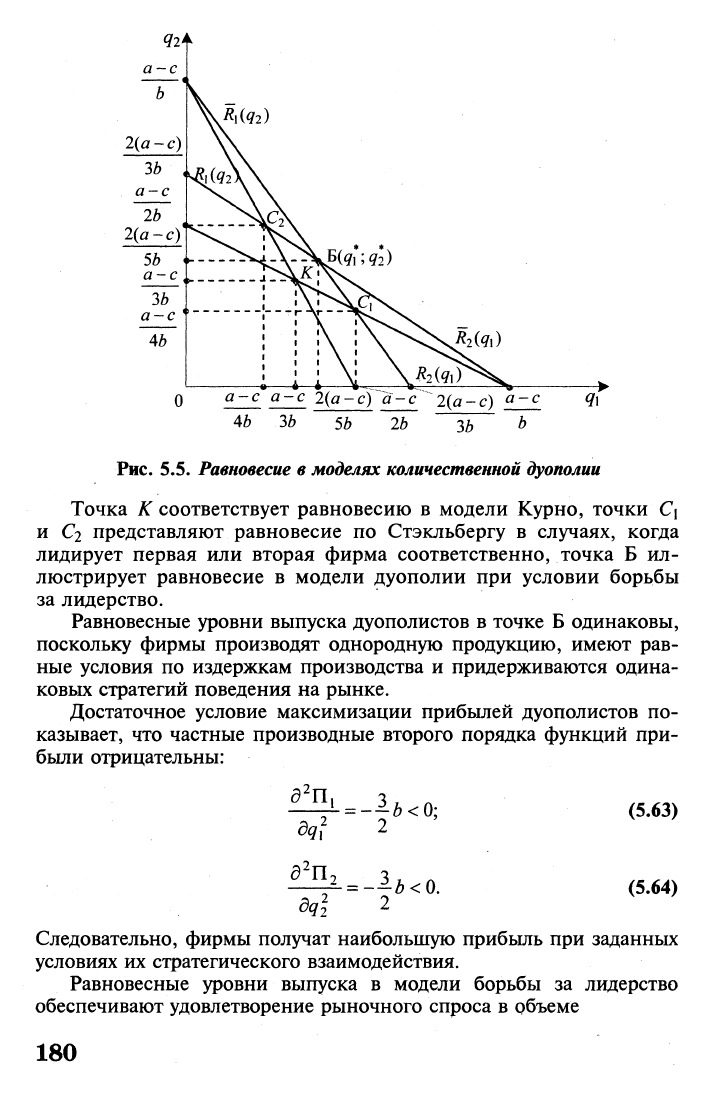
Рис. 5.5.

Равновесие

моделях количественной дуополии

Точка К соответствует равновесию в модели Курно, точки С\

и Ci представляют равновесие по Стэкльбергу в случаях, когда

лидирует первая или вторая фирма соответственно, точка Б ил-

люстрирует равновесие в модели дуополии при условии борьбы

за лидерство.

Равновесные уровни выпуска дуополистов в точке Б одинаковы,

поскольку фирмы производят однородную продукцию, имеют рав-

ные условия по издержкам производства и придерживаются одина-

ковых стратегий поведения на рынке.

Достаточное условие максимизации прибылей дуополистов по-

казывает, что частные производные второго порядка функций при-

были отрицательны:

52п

_1,

<0;

dqf

dq\

-b<0.

(5.63)

(5.64)

Следовательно, фирмы получат наибольшую прибыль при заданных

условиях их стратегического взаимодействия.

Равновесные уровни выпуска в модели борьбы за лидерство

обеспечивают удовлетворение рыночного спроса в объеме

180

л*

-* *

4(я-с)

£? =tfi +

<?2

= .,

(5.65)

при равновесной цене

* _

<з +

4с

" 5 '

что позволяет каждому дуополисту получить прибыль в размере

(5.66)

2(а-с£

25Ь

5.2.5. Модель Бертрана

Одна из классических моделей ценовой олигополии была пред-

ложена Ж. Бертраном как альтернатива стратегического поведения

по отношению

модели Курно. В качестве эндогенных переменных

модели были предложены цены, а не объемы выпуска продукции.

Дуополисты Бертрана вырабатывают решения независимо друг

от друга, принимают уровень цены конкурента как данный,

при

такой предпосылке выбирают решение об уровне своей цены.

Рассмотрим модель дуополии Бертрана

при

предпосылках

(5.7)—(5.9). В процессе решения модели определяется рыночная

цена,

а не

выпуск, поэтому перепишем функцию рыночного

спроса в виде

---;>.

(5.68)

Дуополисты по-прежнему решают задачу на максимум прибыли в ви-

де (5.11), (5.12). Однако по сравнению со случаем количественной дуопо-

лии структура функции прибыли у каждого дуополиста изменится.

Проанализируем для начала стратегию поведения монополиста

Бертрана.

условиях ценовой монополии фирма максимизирует

прибыль вида

= (p-c)Q =

(p-c)f^-^p^

(5.69)

Необходимое условие экстремума

/7+

«±£

= 0

(5.70)

Ъ Ъ

определяет уровень монопольной цены

а + с

(5.71)

181

а следовательно, монопольный уровень выпуска

^£.

(5.72)

2Ь

Достаточное условие экстремума

(5.73)

показывает,

что

монополист получит максимальную прибыль

размере

Если

на

рынке дуополии установлена монопольная цена,

то бы-

ло

бы

разумно считать,

что

дуополисты поделят рынок между

со-

бой. Однако

они

принимают решения независимо друг

от

друга.

Пусть

для

определенности первый дуополист установил цену

на

уровне монопольной,

т.е.

Px=Pm=

- (5.75)

В этом случае его конкурент предпочтет понизить цену. Таким об-

разом, покупатели, привлеченные более низкой ценой, перейдут ко

второму дуополисту, а значит, он должен обеспечить весь рыноч-

ный спрос

Т-Т/>2- (5.76)

Возникает вопрос:

На

сколько нужно понизить цену

по

сравнению

монопольной, чтобы обеспечить себе максимальный уровень прибыли?

Пусть

P2=Pm-b

Y--\,

(5-77)

где \

О.

Тогда второй дуополист Бертрана решает задачу максимизации прибыли

=-(р

-с)(|-1/>

) (5.78)

Заметим,

что

условия (5.71), (5.72), (5.74)

точности соответствуют условиям

(5.23),

(5.22), (5.24),

т.е.

решение монополиста

не

изменяется

при

изменении

эндогенной переменной модели.

182

при условии (5.77). Нужно выбрать такое значение

> О, которое

обеспечит максимум прибыли

^-^

^7Г^-

5Л9

АЬ

Необходимое условие экстремума

^г-т^°

показывает, что максимум прибыли достигается только при

£,

равном нулю, т.е. когда второй дуополист становится монополи-

стом на рынке

Анализ позволяет сделать вывод, что дуополист Бертрана дол-

жен стремиться к понижению цены на бесконечно малую величину £

Это обеспечит ему захват рынка и максимальную прибыль, прибли-

зительно равную монопольной.

Очевидно, что конкурент не захочет мириться

такой ситуаци-

ей.

Тем более что он тоже имеет возможность уменьшить цену, ус-

тановленную

на

рынке, переманить покупателей

себе

обеспе-

чить себе максимальную прибыль при данных условиях принятия

решения.

Существует ли предел понижения цены? Для примера: второй

дуополист будет понижать цену, пока

него есть возможность по-

лучать положительную прибыль, т.е. при

0<£<5Lz£. (5.81)

Наибольшее из возможных значений £ , равное

приведет

понижению цены

до

уровня предельных

средних издержек.

Дальнейшее понижение цены теряет смысл, хотя

принципе

возможно. Ситуация, когда фирмы снижают цены, получая при

этом отрицательную прибыль, получила название «гиперконку-

ренция».

Серия последовательных уменьшений цены конкурирующими

на рынке фирмами получила название

ценовой

войны.

Ценовая вой-

на продолжается до тех пор, пока цена не снизится до уровня сред-

них издержек.

Достаточное условие экстремума

г ,

2__

< 0

подтверждает, что полу-

ченная прибыль будет максимально возможной.

183

Равновесие на рынке дуополии Бертрана достигается, когда ни

один из конкурентов больше не может получать выгоды от сниже-

ния цены, т.е. при цене, равной средним и предельным издержкам:

р*=с.

(5.82)

Это значит, что дуополисты независимо друг от друга назначают

одну и ту же цену, обеспечивая рыночный спрос на уровне:

£*=<71+<72=^, (5-83)

что соответствует ситуации совершенной конкуренции. Конкуренты

не получают положительную прибыль

•

(П

=П

=0) при любом

распределении рыночных долей. Принято считать, что в силу вве-

денных предпосылок об однородности продукции и о равных усло-

виях по издержкам производства дуополисты Бертрана в условиях

равновесия разделят рынок между собой:

Я]=Я2=£

(5,84)

Предпосылка о разделе рынка дуополии Бертрана при равенстве

назначаемых конкурентами цен, как правило, принимается при по-

строении кривой спроса отдельного дуополиста. Спрос на продук-

цию отдельной фирмы формируется следующим образом:

\D{

если pj < pj;

если Р;.=р/,

если Pi > Pj,

A (Pi

>Pj) =

\- D(Pi \ если р

= pj; (5.85)

где Q =

D{p) —

функция рыночного спроса.

Например, функция спроса на продукцию первого дуополиста в

рассматриваемой нами модели имеет вид:

А(АэЛ) =

а 1

Т-тРи

если /?, <р

;

о о

7"7А |>

если

P\=Pi> (5.86)

Ъ Ь

0, если р

Она представлена на рис. 5.6 в виде трех фрагментов. Если /?, > р

то все покупатели уйдут к конкуренту, поэтому вертикальный отре-

зок на оси 0р\ соответствует нулевому уровню выпуска первого дуо-

полиста.

184

Р\

P\>Pi <

Pi=Pi t

Pi <

(

) f

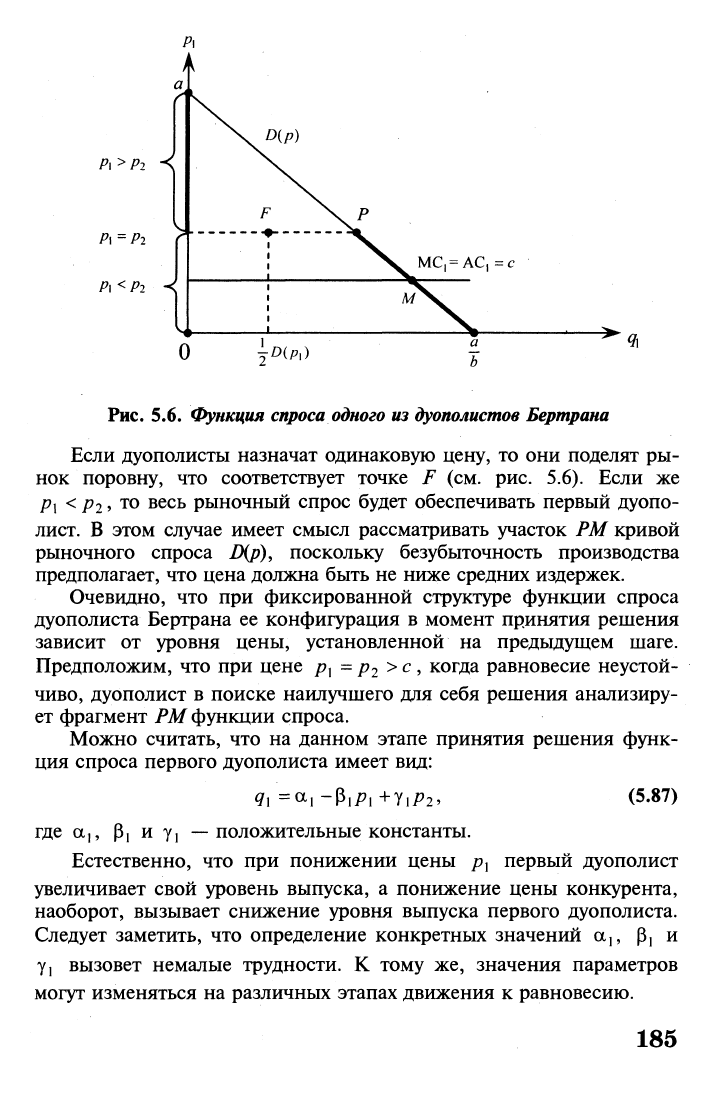
Рис.

5.6.

Функция спроса одного

из

дуополистов Бертрана

Если дуополисты назначат одинаковую цену, то они поделят ры-

нок поровну, что соответствует точке F (см. рис. 5.6). Если же

, то весь рыночный спрос будет обеспечивать первый дуопо-

лист. В этом случае имеет смысл рассматривать участок РМ кривой

рыночного спроса В(р), поскольку безубыточность производства

предполагает, что цена должна быть не ниже средних издержек.

Очевидно, что при фиксированной структуре функции спроса

дуополиста Бертрана ее конфигурация в момент принятия решения

зависит от уровня цены, установленной на предыдущем шаге.

Предположим, что при цене р

= р

с, когда равновесие неустой-

чиво,

дуополист в поиске наилучшего для себя решения анализиру-

ет фрагмент РМ функции спроса.

Можно считать, что на данном этапе принятия решения функ-

ция спроса первого дуополиста имеет вид:

Яг

=ai-PiPi+Yi/>2> <

)

где a,, pj и у,

—

положительные константы.

Естественно, что при понижении цены р

первый дуополист

увеличивает свой уровень выпуска, а понижение цены конкурента,

наоборот, вызывает снижение уровня выпуска первого дуополиста.

Следует заметить, что определение конкретных значений а,, $

У! вызовет немалые трудности. К тому же, значения параметров

могут изменяться на различных этапах движения к равновесию.

185

Если дуополист Бертрана может оценить функцию спроса на

свою продукцию, то его функция прибыли (5.4) примет вид:

П, =(

-c)(a

{

-р,р, +y,p

). (5.88)

В силу предпосылок модели дуополисты Бертрана принимают ре-

шения при нулевых предполагаемых вариациях:

(5.89)

Таким образом, необходимое условие максимизации прибыли

д\\

др\

= -2Pi^i+aj +ф

{

+у

{

= 0

(5.90)

задает линию реакции первого дуополиста

R\(pi)'.

р .р ^

2Р,

У1

2Э,

(5.91)

По аналогии, оценив функцию спроса для второго дуополиста:

можно получить его линию реакции

RjiPxY

72 „ , а

+ср

(5.93)

2р

Предложенная аналитическая версия модели была выбрана, по-

тому что она помогает понять, почему линии реакции дуополистов

Бертрана возрастают в отличие от линий реакции Курно.

Графическая иллюстрация равновесия в модели дуополии Бер-

трана представлена на рис. 5.7.

>с

Р\>с

Рис.

5.7.

Равновесие

модели дуополии

Бертрана:

случай дифференцированных продуктов

186

Следует заметить, что функции спроса дуополистов Бертрана

вида (5.87), (5.92) характерны для случая дифференцированных

продуктов. Поэтому равновесное решение (р*',р

) достигается, ко-

гда цены превышают предельные издержки (см. рис. 5.7).

Рассмотрим случай, когда дуополисты Бертрана производят од-

нородную продукцию. Установление цены ниже средних издержек

приводит к убыточности производства, поэтому линии реакции

дуополистов не определены, если уровни цен ниже АС = МС = с.

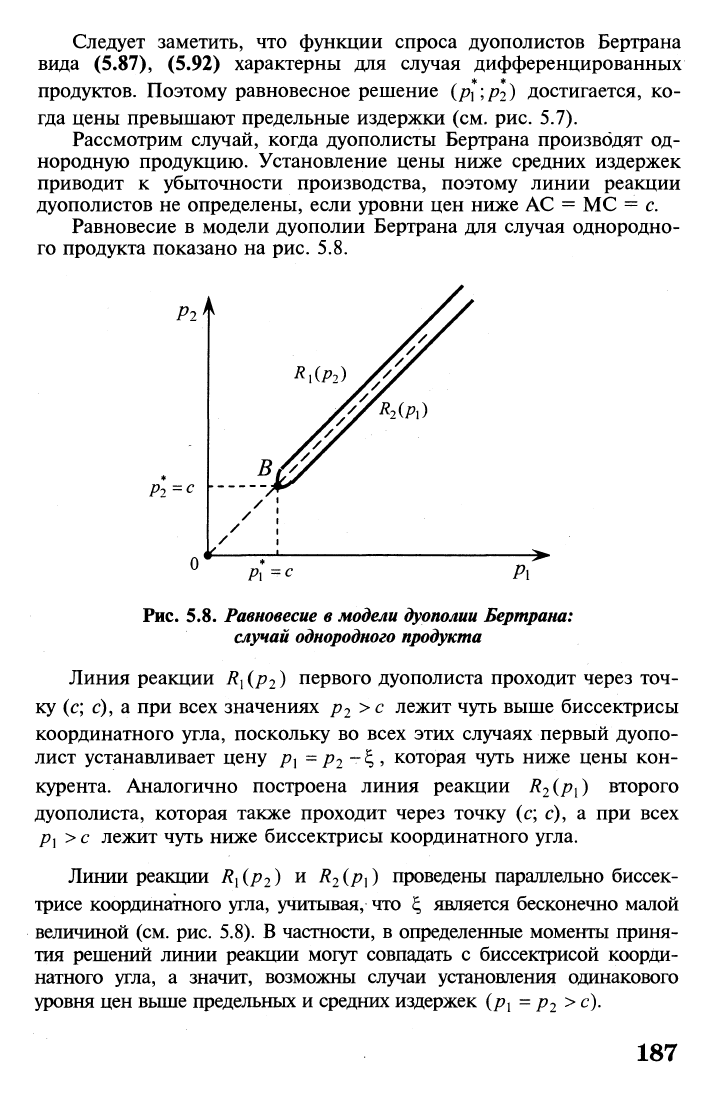
Равновесие в модели дуополии Бертрана для случая однородно-

го продукта показано на рис. 5.8.

р*

=с

;=с

{

Рис. 5.8.

Равновесие

модели дуополии

Бертрана:

случай однородного продукта

Линия реакции

) первого дуополиста проходит через точ-

ку (с; с), а при всех значениях р

>с лежит чуть выше биссектрисы

координатного угла, поскольку во всех этих случаях первый дуопо-

лист устанавливает цену р

-£ , которая чуть ниже цены кон-

курента. Аналогично построена линия реакции R

(P\) второго

дуополиста, которая также проходит через точку (с; с), а при всех

Рх>с лежит чуть ниже биссектрисы координатного угла.

Линии реакции R

{

) и R

) проведены параллельно биссек-

трисе координатного угла, учитывая, что

Ъ,

является бесконечно малой

величиной (см. рис. 5.8). В частности, в определенные моменты приня-

тия решений линии реакции могут совпадать с биссектрисой коорди-

натного угла, а значит, возможны случаи установления одинакового

уровня цен выше предельных и средних издержек (р

{

с).

187

Если принять, что значение § нужно выбирать тем выше, чем

больше превышение цены конкурента над предельными и средни-

ми издержками, то линии реакции дуополистов Бертрана для слу-

чая однородного продукта будут идентичны линиям реакции для

случая дифференцированных продуктов, когда последние располо-

жены выше точки В (см. рис. 5.7).

Равновесие в модели дуополии Бертрана достигается в точке

пересечения линий реакции конкурентов. При данных предпосыл-

ках такая точка существует и определяется однозначно. В точке

равновесия дуополисты Бертрана получают максимально возмож-

ную прибыль

, хотя в случае однородного продукта эта максималь-

но возможная прибыль равна нулю.

Ситуацию равновесия в модели олигополии Бертрана назы-

вают парадоксом Бертрана. Трудно предположить, что при не-

большом числе фирм на рынке (в том числе при дуополии) мож-

но получить конкурентную цену, т.е. фирмы не в состоянии

обеспечить себе положительную прибыль, производя однородную

продукцию.

Модель дуополии Бертрана для случая дифференцированных

продуктов можно также использовать, чтобы показать, что изопро-

фиты дуополистов Бертрана имеют вид, представленный на рис. 5.9.

Каждая изопрофита дуополиста Бертрана выпукла к оси, на кото-

рой отображается уровень его цены.

«(ft)

<sJ^

П?ч

-Д

'т^

4 1 :

Рг

——•

О Р\ О р

Рис. 5.9.

Изопрофиты

линии реакции дуополистов Бертрана

Для любого данного уровня цены конкурента существует един-

ственный уровень цены дуополиста, обеспечивающий максимум его

Для случая дифференцированных продуктов достаточное условие экстремума

подтверждает, что принято наилучшее решение.

188

прибыли. Соответствующие комбинации цен образуют линии реак-

ции R

) и

(P\)*

Конфигурация изопрофит означает, что в случае, когда конку-

рент понижает уровень своей цены, дуополист также должен пони-

зить свою цену, по возможности оставаясь на той же изопрофите,

т.е.

сохраняя прежний уровень прибыли. Чем ближе расположена

изопрофита к оси цены дуополиста, тем меньшему уровню прибы-

ли она соответствует.

Равновесие в модели дуополии Бертрана для случая однородно-

го продукта (см. рис. 5.8) предполагает, что изопрофиты обоих дуо-

полистов, проходящие через точку В(с; с), соответствуют нулевому

уровню прибыли.

5.2.6. Модель Эджуорта

Одно из решений парадокса Бертрана предложил Ф. Эджуорт,

введя ограничения на величину производственной мощности дуо-

полистов. В терминах нашей модели введение ограничений на про-

изводственные мощности фирм означает, что их затраты на произ-

водство дополнительной единицы продукции сверх существующего

уровня мощности бесконечно велики.

Фрэнсис Эджуорт впервые обратил внимание специалистов на

то,

что введение ограничений на производственные мощности

фирм может привести к тому, что единая равновесная цена не будет

установлена, т.е. статическое равновесие по Бертрану может стать

недостижимым. Однако, как показывает дальнейший анализ, ре-

зультат функционирования рынка будет существенно зависеть от

величины ограничений на производственные мощности фирм.

Проиллюстрируем ситуацию на следующем примере. Предпо-

ложим, что в начальный момент времени / = 0 рынок дуополии

находится в состоянии равновесия по Бертрану (5.82)—(5.84), т.е.

дуополисты независимо друг от друга назначили одну и ту же цену

=с и разделили рынок пополам: q\o

fto

^—^-

обеспечивая

2А

рыночный спрос на уровне Q

=#j

+#2o

=^-

^-*

При выбранных

предпосылках это соответствует ситуации совершенной конкуренции:

дуополисты не получают положительную прибыль (Пю = П20 = 0) при

любом распределении рыночных долей. Пусть мощности дуополи-

стов ограничены как раз на уровне половины рыночного спроса

при цене, равной предельным издержкам:

189