Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.


2.2 Atomic Structure of Grain Boundaries 123
as lattice dislocations conserve the crystal lattice when forming a low-angle
grain boundary. As in the most trivial case the CSL will not be changed, if
dislocations are introduced, the Burgers vectors of which are lattice vectors
of the CSL. Equivalently, it is possible that the Burgers vector would be a
vector of the crystal lattice. However, the elastic energy of dislocations in-
creases with the square of the Burgers vector: E
d
∼ b
2
. Therefore, the energy
of the grain boundary would increase dramatically if dislocations with a very
large Burgers vector would be implemented into the grain boundary. How-
ever, the density of coincidence sites will determine only the energy, not their
location. As a consequence we can relax the requirement that the location of
the coincidence sites has to be conserved. There are very small vectors which
conserve the size of the CSL if the location of the coincidence sites are allowed
to change. The displacement vectors which satisfy this condition define the so-
called DSC lattice. DSC is the abbreviation for displacement shift complete.
This means that the CSL will displace as a whole, if one of the two adjacent
crystal lattices is shifted by a translation vector of the DSC lattice. The DSC
lattice is the coarsest grid, which contains all lattice points of both crystal
lattices (Fig. 2.12). Of course, all translation vectors of the CSL and the crys-
tal lattices are also vectors of the DSC lattice, but the elementary vectors of
the DSC lattice are much smaller. Since the dislocation energy increases with
the square of the Burgers vector, only base vectors of the DSC lattice qual-
ify for Burgers vectors of the so-called secondary grain boundary dislocations
(SGBDs). Dislocations with DSC Burgers vectors are referred to as SGBDs,
in contrast to primary grain boundary dislocations, which are crystal lattice
dislocations, the periodic arrangement of which generates the CSL.
SGBDs are confined to grain boundaries, since their Burgers vectors are not
translation vectors of the crystal lattice and their introduction in the crystal
lattice would cause a local destruction of the crystal structure. With regard
to their geometry and correspondingly, to their elastic properties, secondary
grain boundary dislocations can be treated like primary dislocations. As much
as primary dislocations can compensate a misorientation of the perfect crys-
tal by a low-angle grain boundary, so much can secondary grain boundary
dislocations compensate an orientation difference to a CSL relationship while
conserving the CSL. Since SGBDs also have an elastic strain field as does any
dislocation, they can be imaged in a TEM (Fig. 2.13). The larger the orien-
tation difference to the exact coincidence rotation, the smaller the spacing of
the SGBDs according to Eq. (2.1).
SGBSs can be treated with regard to their geometrical and elastic proper-
ties like ordinary dislocations except for their much smaller Burgers vectors
b
B
. The orientation difference Δϕ to the reference CSL orientation relation-
ships is described in complete analogy to Eq. (2.1) by their spacings d
GB
b
B
Δϕ
= d
GB
(2.6)
© 2010 by Taylor and Francis Group, LLC
124 2 Structure of Grain Boundaries
001
001
010
(a)
(b)
(c)
(d)
010
b
D =
ϕ
001
001
010
(a)
(b)
(c)
(d)
010
b
D =
ϕ
b
D =
ϕ
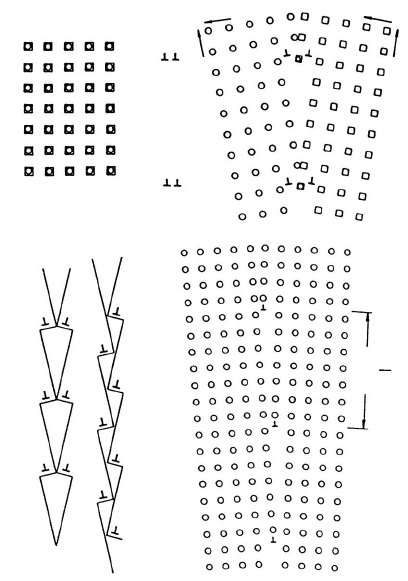
FIGURE 2.11
Relationship between the coincidence site lattice and the primary dislocation
structure at a grain boundary. If two identical, interlocking lattices (a) are
turned symmetrically toward each other about an axis perpendicular to the
plane of the page (b), a coincidence site lattice forms. The coincidence points
are marked by overlapping circles and squares. The associated configuration
of the resulting double dislocation is relaxed along the boundary (c), and the
structure of a symmetrical low-angle tilt boundary forms (d).
© 2010 by Taylor and Francis Group, LLC
2.2 Atomic Structure of Grain Boundaries 125
DSC
CSL
DSC
CSL
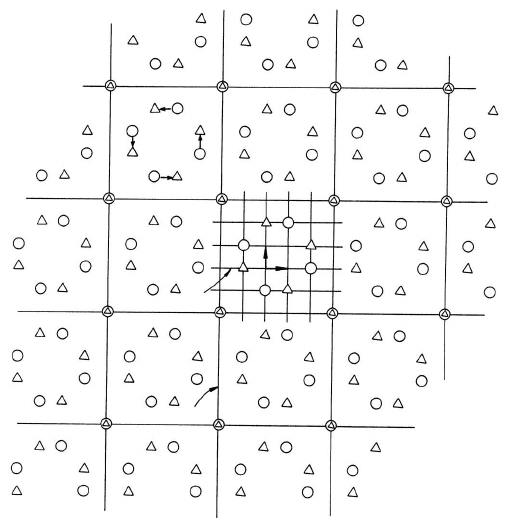
FIGURE 2.12
Coincidence site lattice (CSL) and DSC lattice at 36.9
◦
100 rotation in a
cubic lattice.
© 2010 by Taylor and Francis Group, LLC

126 2 Structure of Grain Boundaries
FIGURE 2.13
Grain boundary dislocations in a tilt boundary in stainless steel (after [175]).
Correspondingly, the energy of a periodic SGBD arrangement γ(Δϕ) adds on
to the energy of the reference CSL structure, according to Eq. (2.3)
γ(ϕ)=γ
CSL
+ γ(Δϕ)=γ
CSL
+Δϕ (A
b
− B
b
ln Δϕ) (2.7)
with A
b
= E
b
c
/b
B
and B
b
=
μb
B
4π(1−ν)
.
The observed cusps of grain boundary energy at CSL orientation relation-
ships (Fig. 2.4) are actually caused by the infinite slope of γ(Δϕ)forΔϕ → 0
owing to the logarithmic dependency.
A special property of the SGBDs is that at the location of the disloca-
tion core the grain boundary usually has a step (Fig. 2.14). This step is a
consequence of the fact that the CSL is displaced when an SGBD is intro-
duced. If an SGBD moves along the grain boundary, the step moves along
with the dislocation and thus, the grain boundary is displaced perpendicular
to its plane, i.e. the grain boundary will migrate by the distance of the step
height. A fundamental property of all dislocations is that they cause a shear
deformation upon their motion. Therefore, the motion of a grain boundary
dislocation will always cause a combination of grain boundary migration and
grain boundary sliding. In the case that the Burgers vector of the SGBD is
parallel to the grain boundary plane the dislocation needs only to glide to have
the grain boundary displaced. This is the case, for instance, in symmetrical
tilt grain boundaries (Fig. 2.14a). If the Burgers vector is inclined to the grain
boundary plane, the dislocation can only move by a combination of glide and
climb (Fig. 2.14b), which requires the diffusion of vacancies, and, therefore, is
a thermally activated process.
The concept introduced is based on geometrical arguments only. Such a con-
© 2010 by Taylor and Francis Group, LLC
2.2 Atomic Structure of Grain Boundaries 127
[010]
[100]
b
b
(a) (b)
[010]
[100]
b
b
(a) (b)
FIGURE 2.14
Atomic configuration of a grain boundary edge dislocation at a Σ = 5 grain
boundary in an fcc lattice. (a) Burgers vector parallel to the grain boundary.
(b) Burgers vector inclined to the grain boundary (after [168]).
sideration cannot make predictions about the force equilibrium of the atomic
arrangements considered. This problem can only be solved by computer sim-
ulations, which allow us to calculate the position of the atoms at an equilib-
rium of interatomic forces, i.e. by relaxation of the geometrical arrangement
[35],[167]–[169] (Fig. 2.15). In contrast to the basis of the geometrical consider-
ations, coincidence almost always gets lost upon relaxation, but the periodicity
remains and that means the conceptual framework is still correct. A more de-
tailed analysis reveals that the arrangement of atoms in the grain boundary
can be described by polyhedra, and surprisingly enough, only seven differ-
ent polyhedra are necessary to describe all possible arrangements of atoms in
a grain boundary [170] (Fig. 2.16). These polyhedra represent characteristic
structures of the grain boundary and are therefore referred to as structural
units. Computer simulations prove that grain boundaries of particularly low
energy consist of only one type of polyhedron. If the orientation relationship
is slightly changed, other structural units (polyhedra) will be introduced into
the structure, and these new structural units are identical with the cores of
the SGBDs (Fig. 2.17). With increasing misorientation the density of the new
structural units increases until they finally will represent the majority and
therefore, on further rotation, the grain boundary structure will eventually
consist of only this type of polyhedron. This structural unit concept of grain
boundaries and its dependence on orientation relationship represents our cur-
rent conception of grain boundary structure [171]. The computer simulations
of grain boundary structure have also been confirmed by high resolution elec-
tron microscopy [172, 173] (Fig. 2.18). Of course, these are considerations
© 2010 by Taylor and Francis Group, LLC

128 2 Structure of Grain Boundaries
(a)
(b)
(c)
(a)
(b)
(c)
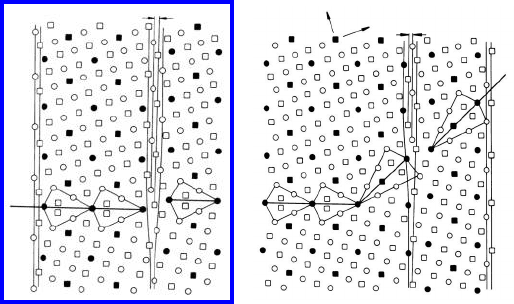
FIGURE 2.15
Structure of a symmetrical 36.9
◦
100(Σ = 5) tilt boundary in aluminum,
calculated by computer simulation: (a) Configuration after rigid rotation of
the crystallites, (b) and (c) structure of grain boundaries after relaxation.
The staggered vertical lines at the grain boundary indicate the shift of the
crystallites. Hence, for a given misorientation there can be more than one
structure (after [168]).
(β)
(γ)(δ)
(ε)(ξ)
(η)
(α) (β)
(γ)(δ)
(ε)(ξ)
(η)
(α)
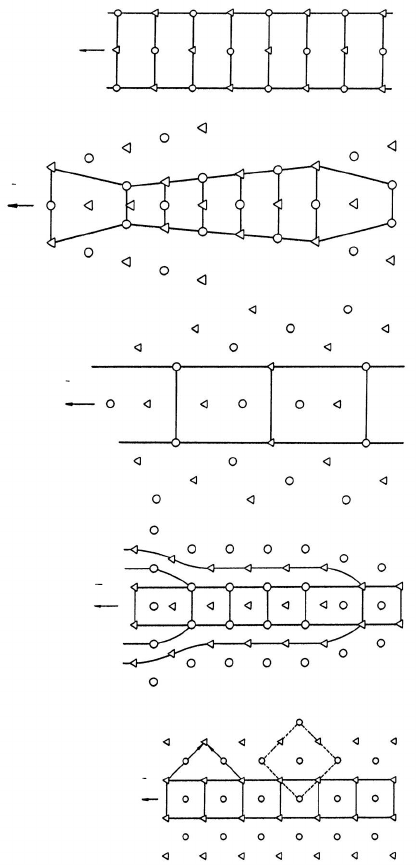
FIGURE 2.16
The seven different Bernal structures that grain boundaries (in structures
formed of hard spheres) can consist of: (α) tetrahedron; (β) octahedron;
(γ) trigonal prism; (δ) truncated trigonal prism; (ε) archimedean square an-
tiprism; (ξ) truncated Archimedeansquareantiprism;(η) pentagonal double
pyramid (after [170]).
© 2010 by Taylor and Francis Group, LLC
2.2 Atomic Structure of Grain Boundaries 129
Σ
=1
(100)
1
/(100)
2
90° [001]
|C.C|
Σ
=25
(710)
1
/(170)
2
73.74° [001]
|BCCCCC|
Σ
=5
(210)
1
/(120)
2
36.87° [001]
|B.B|
Σ
=41
(540)
1
/(450)
2
12.68° [001]
|AAAB.AAAB|
Σ
=1
(110)
1
/(110)
2
0° [001]
|A|
BBAAAA
AAAAAA
C
C
C
C
C
B
B
BBB
CC CCCCC
100 010
010
1
17 0
1
12 0
1
450
1
11 0
Σ
=1
(100)
1
/(100)
2
90° [001]
|C.C|
Σ
=25
(710)
1
/(170)
2
73.74° [001]
|BCCCCC|
Σ
=5
(210)
1
/(120)
2
36.87° [001]
|B.B|
Σ
=41
(540)
1
/(450)
2
12.68° [001]
|AAAB.AAAB|
Σ
=1
(110)
1
/(110)
2
0° [001]
|A|
BBAAAA
AAAAAA
C
C
C
C
C
B
B
BBB
CC CCCCC
100 010
010
1
17 0
1
12 0
1
450
1
11 0
FIGURE 2.17
Calculated dependence of grain boundary structure on the tilt angle of a sym-
metrical 100 tilt boundary in aluminum for various tilt angles. For every tilt
angle there is a certain arrangement of structural units (A,B,C). If this ar-
rangement is interrupted, this forms a grain boundary dislocation (illustrated
for Σ = 41) (after [171]).
© 2010 by Taylor and Francis Group, LLC

130 2 Structure of Grain Boundaries
(a)
(b)
(c)
(a)
(b)
(c)
FIGURE 2.18
Atomic structure of a Σ7 boundary in aluminum: (a) HREM image; (b) sim-
ulated HREM image using the relaxed grain boundary structure; and (c)
computed by molecular dynamics [173].
which do not include the thermal agitation of atoms. In fact, the structure
may change at high homologous temperatures, when entropy becomes impor-
tant, and, indeed, structural phase transformations of low Σ CSL boundaries
(special boundaries) have been reported. Molecular dynamics computer sim-
ulations are now being employed to address this important issue.
© 2010 by Taylor and Francis Group, LLC
2.3 Problems 131
2.3 Problems
PROBLEM 2.1
Compute the surface tension of a low-angle 112 symmetrical tilt grain
boundaries in Al with following angle of misorientation ϕ:0.5
◦
;3
◦
;5
◦
;8
◦
.
PROBLEM 2.2
Find the equilibrium angles at a triple junction with the following grain
boundary energies γ
1
=0.323 J/m
2
; γ
2
=0.620 J/m
2
; γ
3
=0.460 J/m
2
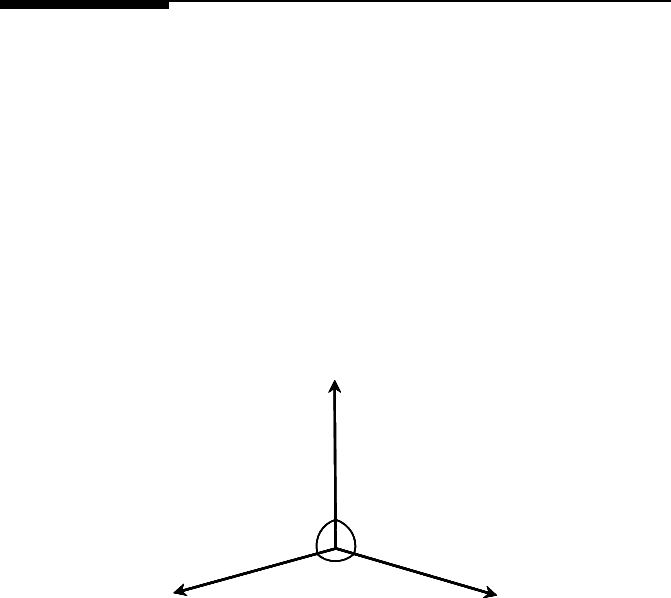
(see Fig. (2.19)).
γ
1
γ
2
γ
3
α
1
α
2
α
3
γ
1
γ
2
γ
3
α
1
α
2
α
3
FIGURE 2.19
Equilibrium of three grain boundaries at a triple junction.
PROBLEM 2.3
Consider a grain boundary to be a supercooled liquid. Use the Clausius-
Clapeyron equation to find the pressure which should be applied to the grain
boundary from the bulk to maintain the grain boundary in a liquid state for:
Al (at 400
◦
C); Pb (at 100
◦
C); Au (at 600
◦
C).
PROBLEM 2.4
Prove that in a uniform 2D grain boundary system a quadruple junction is
unstable.
PROBLEM 2.5
In problem 2.4 it was shown that for uniform grain boundaries quadruple
junctions in a 2D grain boundary system are unstable.
© 2010 by Taylor and Francis Group, LLC
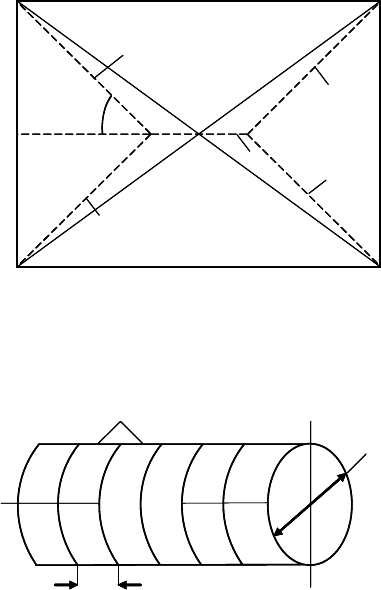
132 2 Structure of Grain Boundaries
a
α
γ
1
γ
1
γ
1
γ
1
γ
2
a
α
γ
1
γ
1
γ
1
γ
1
γ
2
FIGURE 2.20
System of grain boundaries with quadruple junction.
Δχ
0
ϕ
0
Δχ
0
ϕ
0
FIGURE 2.21
Sample with a bamboo grain boundary microstructure.
(a) Find the conditions under which it is possible to maintain a quadruple
junction in the configuration given in Fig. 2.3.
(b) Assume that the Burgers vectors of the grain boundary dislocations are
the same. Find the misorientation of a grain boundary with surface tension
γ
2
, if the misorientation of the first grain boundary is 5
◦
.
(c) Do the same as in (b) but for a misorientation of ϕ
1
=8
◦
.
PROBLEM 2.6
Given a sample with a bamboo structure composed of equidistant low-angle
grain boundaries with uniform misorientation angle ϕ
0
(Fig. 2.21). Grain
growth is assumed to take place by unification of two neighboring grain bound-
aries.
(a) Show that such a process decreases the free energy of the system.
(b) Calculate the driving force for such grain growth.
© 2010 by Taylor and Francis Group, LLC
