Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.

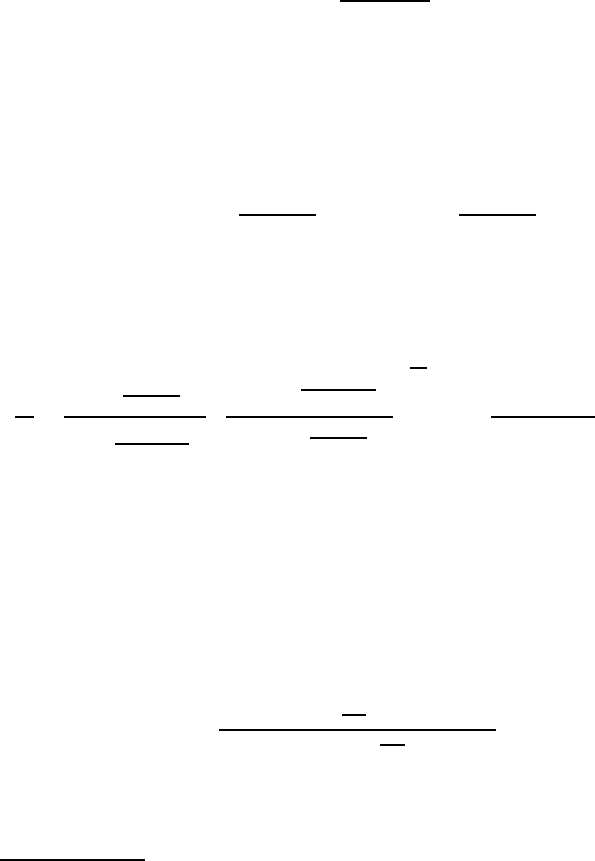
154 3 Grain Boundary Motion
are the partial areas of the atoms of both components in the boundary
6
.Eq.
(3.38) constitutes the general adsorption isotherm, expressed in terms of ac-
tivities. The relation between activity and chemical potentials of components
in real and ideal solutions reads
a
i
= c
i
exp
μ
i
− μ
ideal
i
kT
(3.40)
For consideration of the adsorption of impurities, which interact in the bound-
ary, and bulk solution, we can apply the Bragg-Williams approach for regular
solutions, i.e. entropy changes are neglected.
With the known expressions for the enthalpy of components in a regular
solution the activity in such a solution can be represented as
a
1
= c
1
exp
zε · (c
2
)
2
kT
,a
2
= c
2
exp
zε · (c
1
)
2
kT
(3.41)
where z is the coordination number, ε = ε
12
− 1/2(ε
11
+ ε
22
) is the heat of
mixing and ε
ij
(i, j=1,2) are the interaction enthalpies of the components.
Eqs. (3.38) and (3.41) yield for a regular solution in both bulk and boundary
c
b
1
c
1
=
exp
zε·(c
2
)
2
kT
exp
z
b
ε
b
·
(
c
b
2
)
2
kT
⎡
⎢
⎢
⎣
c
b
2
exp
z
b
ε
b
·
(
c
b
1
)
2
kT
c
2
exp
zε·(c
1
)
2
kT
⎤
⎥
⎥
⎦
ω
1
ω
2
· exp
ω
1
(γ
1
− γ
2
)
kT
(3.42)
where ε
b
,z
b
are the heat of mixing and the coordination number in the grain
boundary, respectively.
Some special cases are of particular interest for an analysis of experimental
results.
1. Both (bulk and boundary) solutions are regular (i.e. the heat of mixing
and coordination number in both solutions are the same) and the partial
areas of the different species in the boundary are equal, i.e. ε
b
= ε, z
b
= z,
ω
1
= ω
2
= ω.
Then
c
b
1
=
Bc
1
exp
2zε
kT
c
b
1
− c
1
1 − c
1
+ Bc
1
exp
2zε
kT
c
b
1
− c
1
(3.43)
where B = e
ω
(
γ
2
−γ
1/kT
)
= B
0
e
H
i
/kT
, H
i
is the enthalpy of interaction between
the boundary and an adsorbed impurity atom.
6
It should be pointed out that the partial areas as defined by Eq. (3.39) are in general
not identical with the physical area fraction occupied by the respective elements in the
boundary but are thermodynamical quantities exactly defined by this equation and may
even assume negative values.
© 2010 by Taylor and Francis Group, LLC
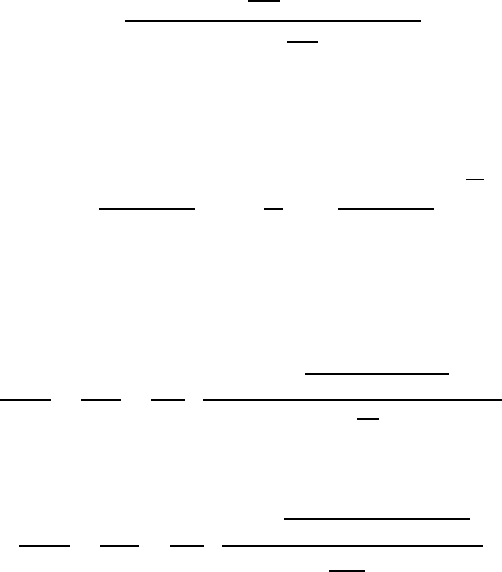
3.3 Drag Effects During Grain Boundary Motion 155
2. The bulk solution is ideal, whereas the boundary solution is regular, i.e.
ε =0,ε
b
=0,ω
1
= ω
2
= ω.Inthiscase
c
b
1
=
Bc
1
exp
z
b
ε
b
kT
2c
b
1
− c
1
1 − c
1
+ Bc
1
exp
z
b
ε
b
kT
2c
b
1
− c
1
(3.44)
For c
1
1, Eq. (3.44) is known as the Fowler-Guggenheim isotherm.
3. The same as case 2, but the partial areas of the species in the boundary
are different, i.e. ε =0,ε
b
=0,ω
1
= ω
2
.Inthiscase
c
b
1
= c
1
exp
−
z
b
ε
b
·
c
b
2
2
kT
· B
c
b
2
c
2
exp
z
b
ε
b
·
c
b
1
2
kT
ω
1
ω
2
(3.45)
The condition closest to experiments is the case of an ideal bulk and a reg-
ular boundary solution. From Eqs. (3.35) and (3.44) (denoting the impurity
concentration as c and using the values for ε and z in the boundary)
m
b
=
m
im
c
b
− c
∼
=
m
im
c
b
=
m
0
B
0
c
·
exp
−
H
D
+H
i
+zε
(
2c
b
−1
)
kT
*
1 − c + Bc exp
zε
kT
(2c
b
− 1)
+
−1
(3.46)
For ω
1
= ω
2
Eqs. (3.33) and (3.44) yield
m
b
=
m
im
c
b
− c
∼
=
m
im
c
b
=
m
0
B
0
c
·
exp
−
H
D
+H
i
+(β−1)zε
(
1−c
b
)
2
kT
1−c
b
1−c
β
(3.47)
with β = ω
2
/ω
1
. An important consequence of Eqs. (3.46) and (3.47) is that
the migration activation enthalpy includes the enthalpy H
D
of impurity mo-
tion involved in boundary migration, the adsorption energy H
i
(segregation
of atoms in the pure boundary) and, in particular, the energy of interaction
between adsorbed atoms. Therefore, the activation enthalpy of grain bound-
ary migration becomes dependent on concentration, as indeed is observed in
experiment (Fig. 3.8).
Figs. 3.9 and 3.10 show the dependence of boundary mobility and its pa-
rameters (A
0
,H) on impurity concentration for 38.2
◦
and 40.5
◦
111 tilt grain
boundaries as obtained by experiment and as calculated from Eqs. (3.46) and
(3.47), respectively. The calculations are in a good agreement with experiment
at reasonable values of H
D
, H
i
and zε. (The magnitude of B
0
=exp(−S/k)
changes in a very narrow range and was taken to be B
0
=5.)
The best agreement between theory and experiment for the concentration
dependence of boundary mobility was found for the isotherm, which takes into
account a difference of the partial areas of the components in the boundary
© 2010 by Taylor and Francis Group, LLC
156 3 Grain Boundary Motion
(b)
(a)
10
-5
10
-4
10
-3
c[at.%]
0.5
1.0
1.5
2.0
2.5
3.0
H[eV]
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
40.5°<111>
38.2°<111>
10
-5
10
-4
10
-3
c[at.%]
10
-10
10
-9
10
-8
10
-7
10
-6
A[m²/s]
40.5°
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
38.2°
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
T = 450°C
38.2°
40.5°
10
-5
10
-4
10
-3
c[at.%]
350
400
450
500
550
600
T
c
[°C]
10
-5
10
-4
10
-3
350
400
450
500
550
600
10
-5
10
-4
10
-3
c[at.%]
0.0
0.2
0.4
0.6
0.8
1.0
c
b
10
-5
10
-4
10
-3
0.0
0.2
0.4
0.6
0.8
1.0
38.2°
40.5°
10
-5
10
-4
10
-3
c[at.%]
10
0
10
2
10
4
10
6
10
8
10
10
A
o
[m²/s]
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
40.5°<111>
38.2°<111>
3.0
2.5
2.0
1.5
1.0
0.5
H
m
[eV]
10
-5
10
-4
10
-3
c[at.%]
40.5°<111>
38.2°<111>
10
-5
10
-4
10
-3
c [at.%]
38.2°<111>
40.5°<111>
10
0
10
2
10
4
10
6
10
8
10
10
A
0
[m
2
/s]
10
-5
10
-4
10
-3
c[at.%]
T=450°C
38.2°
40.5°
38.2°
40.5°
10
-6
10
-7
10
-8
10
-9
10
-10
A
b
[m
2
/s]
10
-5
10
-4
10
-3
c [at.%]
600
550
500
450
400
350
T
c
[°C]
38.2°
40.5°
1.0
0.8
0.6
0.2
0.4
0.0
10
-5
10
-4
10
-3
c[at.%]
(d)(c)
(e)
c
b
A
m
Bc
1- c +Bc exp
z
kT
(2c 1)
0
0
0
b
=⋅ −
L
N
M
Ο
Q
P
R
S
T
U
V
W
σε
H
m
=H
D
+H
i
+z (2c
b
-1)
ε
(c)
(d)
(e)
(a)
(b)
()
b
0
0
0
m
z
A 1 c Bcexp 2c 1
Bc kT
γ
ε
=−+ −
()
b
mDi
HHHz2c1
=++ε −
(b)
(a)
10
-5
10
-4
10
-3
c[at.%]
0.5
1.0
1.5
2.0
2.5
3.0
H[eV]
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
40.5°<111>
38.2°<111>
10
-5
10
-4
10
-3
c[at.%]
10
-10
10
-9
10
-8
10
-7
10
-6
A[m²/s]
40.5°
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
38.2°
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
T = 450°C
38.2°
40.5°
10
-5
10
-4
10
-3
c[at.%]
350
400
450
500
550
600
T
c
[°C]
10
-5
10
-4
10
-3
350
400
450
500
550
600
10
-5
10
-4
10
-3
c[at.%]
0.0
0.2
0.4
0.6
0.8
1.0
c
b
10
-5
10
-4
10
-3
0.0
0.2
0.4
0.6
0.8
1.0
38.2°
40.5°
10
-5
10
-4
10
-3
c[at.%]
10
0
10
2
10
4
10
6
10
8
10
10
A
o
[m²/s]
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
40.5°<111>
38.2°<111>
3.0
2.5
2.0
1.5
1.0
0.5
H
m
[eV]
10
-5
10
-4
10
-3
c[at.%]
40.5°<111>
38.2°<111>
10
-5
10
-4
10
-3
c [at.%]
38.2°<111>
40.5°<111>
10
0
10
2
10
4
10
6
10
8
10
10
A
0
[m
2
/s]
10
-5
10
-4
10
-3
c[at.%]
T=450°C
38.2°
40.5°
38.2°
40.5°
10
-6
10
-7
10
-8
10
-9
10
-10
A
b
[m
2
/s]
10
-5
10
-4
10
-3
c [at.%]
600
550
500
450
400
350
T
c
[°C]
38.2°
40.5°
1.0
0.8
0.6
0.2
0.4
0.0
10
-5
10
-4
10
-3
c[at.%]
(d)(c)
(e)
c
b
A
m
Bc
1- c +Bc exp
z
kT
(2c 1)
0
0
0
b
=⋅ −
L
N
M
O
Q
P
R
S
T
U
V
W
σε
H
m
=H
D
+H
i
+z (2c
b
-1)
ε
(c)
(d)
(e)
(a)
(b)
(b)
(a)
10
-5
10
-4
10
-3
c[at.%]
0.5
1.0
1.5
2.0
2.5
3.0
H[eV]
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
40.5°<111>
38.2°<111>
10
-5
10
-4
10
-3
c[at.%]
10
-10
10
-9
10
-8
10
-7
10
-6
A[m²/s]
40.5°
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
38.2°
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
T = 450°C
38.2°
40.5°
10
-5
10
-4
10
-3
c[at.%]
350
400
450
500
550
600
T
c
[°C]
10
-5
10
-4
10
-3
350
400
450
500
550
600
10
-5
10
-4
10
-3
c[at.%]
0.0
0.2
0.4
0.6
0.8
1.0
c
b
10
-5
10
-4
10
-3
0.0
0.2
0.4
0.6
0.8
1.0
38.2°
40.5°
10
-5
10
-4
10
-3
c[at.%]
10
0
10
2
10
4
10
6
10
8
10
10
A
o
[m²/s]
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
40.5°<111>
38.2°<111>
3.0
2.5
2.0
1.5
1.0
0.5
H
m
[eV]
10
-5
10
-4
10
-3
c[at.%]
40.5°<111>
38.2°<111>
10
-5
10
-4
10
-3
c [at.%]
38.2°<111>
40.5°<111>
10
0
10
2
10
4
10
6
10
8
10
10
A
0
[m
2
/s]
10
-5
10
-4
10
-3
c[at.%]
T=450°C
38.2°
40.5°
38.2°
40.5°
10
-6
10
-7
10
-8
10
-9
10
-10
A
b
[m
2
/s]
10
-5
10
-4
10
-3
c [at.%]
600
550
500
450
400
350
T
c
[°C]
38.2°
40.5°
1.0
0.8
0.6
0.2
0.4
0.0
10
-5
10
-4
10
-3
c[at.%]
(d)(c)
(e)
c
b
A
m
Bc
1- c +Bc exp
z
kT
(2c 1)
0
0
0
b
=⋅ −
L
N
M
O
Q
P
R
S
T
U
V
W
σε
H
m
=H
D
+H
i
+z (2c
b
-1)
ε
(c)
(d)
(e)
(a)
(b)
()
b
0
0
0
m
z
A 1 c Bcexp 2c 1
Bc kT
γ
ε
=−+ −
()
b
mDi
HHHz2c1
=++ε −
FIGURE 3.9
Experimental data (points) and results of calculations (lines) based on Eq.
(3.41) for two 111 tilt grain boundaries in Al. Dependence of (a) activation
enthalpy H
m
; (b) preexponential factor A
0
; (c) reduced boundary mobility A
b
;
(d) compensation temperature T
c
; (e) impurity concentration in the boundary
c
b
on the bulk impurity content c. Parameters used for 38.2
◦
111 boundary:
H
D
=0.6eV;H
i
=0.84eV;(zε) = 0.17 eV; (m
0
γ)=8·10
−5
m
2
/s, and for
40.5
◦
111: H
D
=1.5eV;H
i
=0.82eV;(zε) = 0.21 eV; (m
0
γ)=90m
2
/s.
© 2010 by Taylor and Francis Group, LLC
3.3 Drag Effects During Grain Boundary Motion 157
10
-5
10
-4
10
-3
c [at. %]
10
0
10
2
10
4
10
6
10
8
10
10
A
o
[m²/s]
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
40.5°<111>
38.2°<111>
10
-5
10
-4
10
-3
c [at. %]
350
400
450
500
550
600
T
c
[°C]
10
-5
10
-4
10
-3
350
400
450
500
550
600
10
-5
10
-4
10
-3
c [at.%]
10
-5
10
-4
10
-3
c [at.%]
H
m
=H
D
+ H
i
+z (2c
b
-1)
ε
600
550
500
450
400
350
T
c
[°C]
(d)
10
-5
10
-4
10
-3
c [at. %]
0.5
1.0
1.5
2.0
2.5
3.0
H [eV]
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
38.2°<111>
40.5°<111>
c [at.%]
40.5° <111>
38.2° <111>
(a)
3.0
2.5
2.0
1.5
1.0
0.5
H
m
[eV]
(b)
10
0
10
2
10
4
10
6
10
8
10
10
A
0
[m
2
/s]
10
-5
10
-4
10
-3
c [at. %]
10
-10
10
-9
10
-8
10
-7
10
-6
A [m²/s]
38.2°<111>
40.5°<111>
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
T = 450°C
40.5°
38.2°
c [at.%]
10
-10
10
-6
10
-7
10
-8
10
-9
A
b
[m
2
/s]
(c)
40.5°
38.2
°
T = 450°C
10
-5
10
-4
10
-3
c [at. %]
0.0
0.2
0.4
0.6
0.8
1.0
c
b
10
-5
10
-4
10
-3
0.0
0.2
0.4
0.6
0.8
1.0
38.2°
40.5°
10
-5
10
-4
10
-3
c [at.%]
1.0
0.8
0.6
0.2
0.4
0.0
(e)
c
b
40.5°
38.2°
38.2° <111>
40.5° <111>
10
-5
10
-4
10
-3
10
-3
10
-5
10
-4
A
m
Bc
0
0
0
=⋅
F
H
G
G
I
K
J
J
γ
β
1- c
b
1- c
-
10
-5
10
-4
10
-3
c [at. %]
10
0
10
2
10
4
10
6
10
8
10
10
A
o
[m²/s]
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
10
-5
10
-4
10
-3
10
0
10
2
10
4
10
6
10
8
10
10
40.5°<111>
38.2°<111>
10
-5
10
-4
10
-3
c [at. %]
350
400
450
500
550
600
T
c
[°C]
10
-5
10
-4
10
-3
350
400
450
500
550
600
10
-5
10
-4
10
-3
c [at.%]
10
-5
10
-4
10
-3
c [at.%]
H
m
=H
D
+ H
i
+z (2c
b
-1)
ε
600
550
500
450
400
350
T
c
[°C]
(d)
10
-5
10
-4
10
-3
c [at. %]
0.5
1.0
1.5
2.0
2.5
3.0
H [eV]
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
10
-5
10
-4
10
-3
0.5
1.0
1.5
2.0
2.5
3.0
38.2°<111>
40.5°<111>
c [at.%]
40.5° <111>
38.2° <111>
(a)
3.0
2.5
2.0
1.5
1.0
0.5
H
m
[eV]
(b)
10
0
10
2
10
4
10
6
10
8
10
10
A
0
[m
2
/s]
10
-5
10
-4
10
-3
c [at. %]
10
-10
10
-9
10
-8
10
-7
10
-6
A [m²/s]
38.2°<111>
40.5°<111>
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
10
-5
10
-4
10
-3
10
-10
10
-9
10
-8
10
-7
10
-6
T = 450°C
40.5°
38.2°
c [at.%]
10
-10
10
-6
10
-7
10
-8
10
-9
A
b
[m
2
/s]
(c)
40.5°
38.2
°
T = 450°C
10
-5
10
-4
10
-3
c [at. %]
0.0
0.2
0.4
0.6
0.8
1.0
c
b
10
-5
10
-4
10
-3
0.0
0.2
0.4
0.6
0.8
1.0
38.2°
40.5°
10
-5
10
-4
10
-3
c [at.%]
1.0
0.8
0.6
0.2
0.4
0.0
(e)
c
b
40.5°
38.2°
38.2° <111>
40.5° <111>
10
-5
10
-4
10
-3
10
-3
10
-5
10
-4
A
m
Bc
0
0
0
=⋅
F
H
G
G
I
K
J
J
γ
β
1- c
b
1- c
-
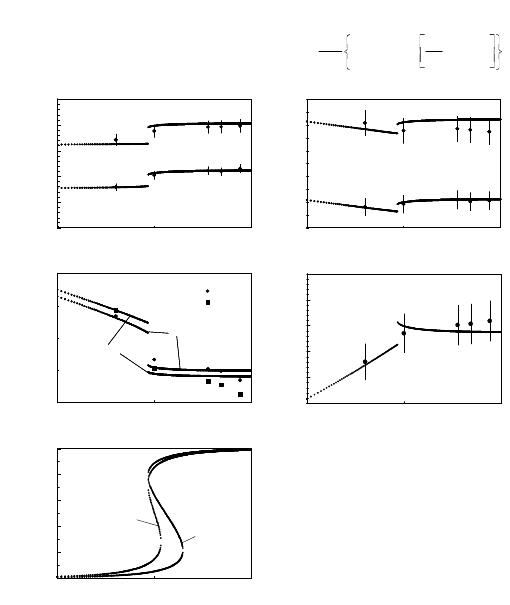
FIGURE 3.10
Experimental data (points) and results of calculations (lines) based on
Eq. (3.42) (β =0.05) for two 111 tilt grain boundaries in Al. Dependence of
(a) activation enthalpy H
m
; (b) preexponential factor A
0
; (c) reduced bound-
ary mobility A
b
; (d) compensation temperature T
c
; (e) impurity concentra-
tion in the boundary c
b
on the bulk impurity content c. Parameters used for
38.2
◦
111 boundary: H
D
=0.68eV;H
i
=0.86eV;(zε) = 0.17 eV; and for
40.5
◦
111: H
D
=1.57eV;H
i
=0.86eV;(zε) = 0.24 eV.
© 2010 by Taylor and Francis Group, LLC

158 3 Grain Boundary Motion
with β = 0.05 and the fitting parameters as given in the Fig. 3.10 caption.
This becomes particularly obvious from Fig. 3.10. It is interesting that the
fit parameter m
0
γ for the Σ7 boundary amounts to m
0
γ =3· 10
−4
m
2
/s.
The term m
0
γ represents the reduced mobility of the boundary in the pure
matrix. If boundary migration would proceed by the transfer of individual
atoms across the boundary from the shrinking to the growing grain, then m
0
ought to follow simple rate theory, i.e. m
0
γ ≡ 10
−5
forAl.Forthesame
reason the activation energy for a jump across the boundary ought to be com-
parable to the activation energy of grain boundary diffusion, i.e. for Al in
the range of 0.6–0.7 eV for the Σ7 boundary. Obviously, the motion of the
special boundary Σ7 is reasonably described in the framework of this simple
theory, and the experimentally observed deviations of H
D
and A
0
from rate
theory can be attributed to the effect of segregated impurities according to
the theory outlined above. Non-special boundaries, in this case the 40.5
◦
111
boundary, behave quite differently: both the activation energy for grain bound-
ary motion (H
D
= 1.57 eV) and the preexponential reduced mobility factor
(m
0
γ =3.5 · 10
2
m
2
/s) are much higher (even orders of magnitude for m
0
γ)
than expected for grain boundary motion caused by the exchange of individ-
ual atoms across the boundary. This indicates that the mechanism of grain
boundary motion at least in this non-special boundary is different from the
migration of special boundaries. In fact, the magnitude of activation energy
and preexponential factor as well as other experimental results for the non-
special boundary hint at a correlated or cooperative motion of atoms during
boundary migration.
3.3.4 Vacancy Drag
Not only impurities may interact with and segregate to grain boundaries.
The same principle holds for intrinsic defects, like vacancies. In principle,
vacancy drag can be treated completely in analogy to impurity drag. However,
it is complicated by the fact that there is no conservation rule for vacancies;
rather, vacancies may be produced and eliminated [198]–[200]. In fact, there
is experimental evidence that grain boundaries can act as sources and sinks
for vacancies [200, 201]. If there is a concentration c
s
of sites which may act as
sinks or sources (imagine a ledge on the crystallite surface in the boundary)
then the production rate for vacancies is
˙q
+
= c
s
νc
∗
exp
−
H
FB
+ H
DB
kT
(3.48)
where ν is a frequency factor, c
∗
an entropy factor, H
FB
and H
DB
represent
the activation enthalpy for grain boundary vacancy formation and diffusion,
respectively.
© 2010 by Taylor and Francis Group, LLC

3.3 Drag Effects During Grain Boundary Motion 159
The annihilation rate is given by
˙q
−
=
c
vb
τ
= c
vb
· c
s
ν exp
−
H
DB
kT
(3.49)
where c
vb
is the actual vacancy concentration and τ the lifetime of a vacancy
in the boundary. The net production rate of boundary vacancies reads
˙q
b
=˙q
+
− ˙q
−
= −
c
vb
− c
e
vb
τ
(3.50)
In equilibrium, ˙q =0andthus,c
vb
= c
e
vb
, i.e. the equilibrium concentration
of vacancies in the boundary.
Another source of vacancy production is the annihilation of dislocations in
the boundary, since each atom on a dislocation line carries an excess volume of
about one atomic volume. Each atom on the dislocation line can, therefore, be
considered to produce one vacancy upon absorption of the dislocation in the
grain boundary, for instance during primary recrystallization. For a (uniform)
dislocation density ρ and a grain boundary migration rate v, the vacancy
production rate by dislocation absorption in the boundary is
˙q
d
= αbρv (3.51)
where the dimensionless factor α ≡ 1 is the number of vacancies formed per
dislocation site. Since the grain boundary also carries an excess volume its
motion will be accompanied by a production of vacancies, e.g. during grain
growth. In fact, such vacancy generation was observed in molecular dynamics
computer simulations of a shrinking half-loop grain boundary [201, 202]. If
the number of vacancies is not conserved, the diffusion equation (Eq.(3.19))
has to be modified to include the vacancy production term ˙q which is only
nonzero in the grain boundary
∂c
∂t
= D
∂
2
c
∂x
2
+
∂
∂x
Dc
kT
dU
dx
+˙q (3.52)
For a potential well as defined by Eq.(3.20) we obtain for the steady state in
the reference frame of the moving boundary
∂c
∂t
= D
∂
2
c
∂x
2
+ v
∂c
∂x
+˙q = 0 (3.53)
The problem can be treated exactly as for impurities previously, except that
the flux equations through the borders of the boundary now read (one atomic
boundary)
j
B/II
= j
II
(3.54a)
j
I/B
= j
B/II
− ˙qb = j
II
− ˙qb (3.54b)
j
I
= j
I/B
= j
II
− ˙qb (3.54c)
© 2010 by Taylor and Francis Group, LLC

160 3 Grain Boundary Motion
or in terms of jump frequencies
c
vb
D
b
e
−H
0
/kT
− c
2
·
D
b
− vc
2
= −vc
0
(3.55a)
c
1
D
b
− c
vb
D
b
e
−H
0
/kT
− vc
vb
= −vc
0
− ˙qb (3.55b)
Again this can be solved for c
1
, c
2
and c
vb
.
The migration rate is again obtained from
v = bν
⎧
⎨
⎩
exp
−
H
m
−Pb
3
/2−H
0
(c
2
−c
vb
)/2
kT
−exp
−
H
m
−Pb
3
/2+H
0
(c
vb
−c
1
)/2
kT
⎫
⎬
⎭
(3.56)
which cannot be solved analytically, since c
1
, c
2
and c
vb
depend on v.Inthe
limit of high (v
F
)andlow(v
L
) velocities, assuming vacancy production by
dislocation absorption we obtain the approximate solutions
v
F
=
b
2
D
m
kT
P −
αρH
0
2b
; v
L
=
2b
2
D
H
0
(c
e
vb
− c
0
)
P (3.57)
where c
e
vb
= c
0
exp (H
0
/kT ). With Φ = bv/D, h = H
0
/2b
3
,Ψ=e
−H
0
/kT
,
γ = b
2
/τD, λ = αρb
2
,andΘ=kT/b
3
.(D/D
m
) the following cases can be
distinguished:
(a) Dislocation type sources but no sinks (γ =0,λ=0)
In this case one obtains for a one-atomic boundary the concentrations
c
1
= c
0
+ λ; (3.58a)
c
vb
=
1+Φ
Ψ+Φ
(c
0
+ λ) ; (3.58b)
c
2
= c
0
−
Φ(1+Ψ)c
0
− Ψ(1+Φ)λ
(1+Φ)(Ψ+Φ)
(3.58c)
Eq. (3.58a) shows that now the concentration c
1
left behind the boundary is
larger than the initial concentration c
0
, it also includes the vacancies contained
in the dislocations (λ). The difference c
1
− c
2
which is proportional to the
retarding force P
v
= α · ρH
0
/(2b) (Eq.(3.57)) is zero for Φ = 0 and λ for
Φ=∞. For small values of Φ, P
v
runs through a maximum, whereas for large
Φ a continuous increase occurs.
The equation f(Φ,P) = 0 is again of third order, and the approximations
Φ
F
and Φ
L
Φ
F
=
P
Θ
−
hλ
Θ
+
h
P
{(c
0
+ λ)Ψ− c
0
}→
P − hλ
Θ
Φ
L
=
P
h (c
0
+ λ − c
0
Ψ) /Ψ+Θ
∼
=
P
h (c
0
+ λ) /Ψ − hc
0
(3.59)
© 2010 by Taylor and Francis Group, LLC
3.3 Drag Effects During Grain Boundary Motion 161
Of interest here is the case that the driving force P is also proportional to the
dislocation density λ as in the case of primary recrystallization. Here P = σ
d
λ
with σ
d
being roughly the energy per dislocated atom divided by b
3
. Then the
function Φ(λ) instead of Φ(P ) has to be considered which contains two aspects
of the dislocation density λ: the dislocations supply a driving force and thus
accelerate the boundary, and they supply vacancies which retard the bound-
ary. For σ
d
>hthe accelerating influence dominates and the expressions for
Φ
F
and Φ
L
remain valid. For σ
d
<h, i.e. for dominance of the retarding
effect, only Φ
L
stays correct, whereas for high velocities there is no longer a
proportionality between Φ and λ, but a plateau value Φ
p
arises. This case,
however, is improbable.
(b) Boundary sources with infinite rates (γ = ∞)
Now let us consider the opposite limiting case, where sources and sinks exist in
the boundary and where the formation and annihilation frequency of vacancies
is extremely high (γ = ∞). With Φc
e
vb
= c
e
v
, the equilibrium concentration in
the lattice, it follows
c
1
=
c
e
v
+ c
e
vb
Φ
1+Φ
; c
vb
= c
e
vb
; c
2
= c
0
−
c
1
− c
e
v
1+Φ
(3.60)
One recognizes that, due to the high source rate, the boundary layer always
exhibits the (boundary) equilibrium concentration c
e
vb
. In the neighboring
plane 2 for Φ = 0 the (lattice) equilibrium concentration c
2
= c
e
v
is found,
whereas for Φ = ∞ again c
2
= c
e
v
. Depending upon whether c
e
v
<c
0
or c
e
v
>c
0
,
a concentration dip or concentration peak occurs. Most interesting, however,
is the concentration of vacancies c
1
left behind the boundary. Also here for
Φ = 0 the lattice equilibrium value c
1
= c
e
vb
, but for Φ = ∞ the boundary
equilibrium value c
e
v
is obtained. Since c
e
vb
and c
e
v
are mostly larger than c
0
,
this means that also here the boundary leaves more vacancies behind than
existed in the original crystal.
The equation f(Φ,P) = 0 now becomes second order in Φ and the resulting
approximate solutions are
Φ
h
=
P
Θ
−
h
Θ
(c
e
vB
− c
0
)+
h
P
(c
e
vb
− c
0
) →
P − hc
e
vb
Θ
(3.61a)
Φ
L
=
P
Θ+h (c
e
vb
− c
0
)
∼
=
P
hc
e
vb
(3.61b)
It must be noted that Eqs. (3.60) and (3.61) do not depend upon λ and are
valid for the cases λ = 0 as well as λ = 0. This means that, because of the
infinitely high rate for establishing equilibrium, it does not matter whether a
few vacancies (more or less) have to be accommodated.
(c) The general case (λ =0; 0<γ<∞)
This case is only little more complicated and contains no new features in
© 2010 by Taylor and Francis Group, LLC

162 3 Grain Boundary Motion
PP
ΦΦ
Φ
L
Φ
H
Φ
H
Φ
L
(a) (b)
PP
ΦΦ
Φ
L
Φ
H
Φ
H
Φ
L
(a) (b)
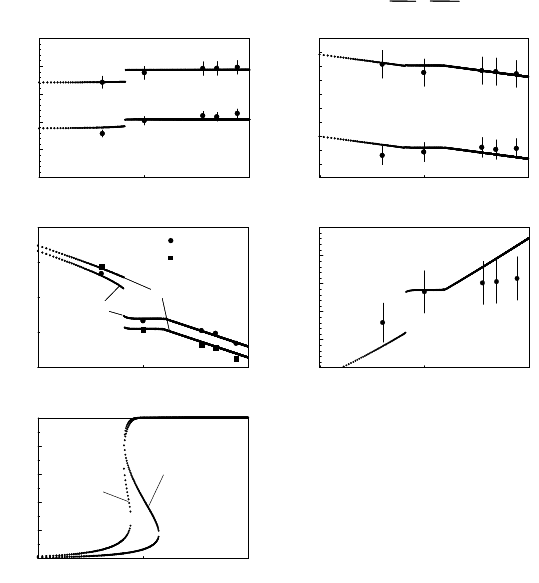
FIGURE 3.11
Normalized grain boundary migration rate Φ vs. driving force in the presence
of vacancy drag. (a) Low drag force; (b) high drag force.
addition to those already discussed. One obtains for the concentrations
c
1
=
Ψ − Φ
1+Φ
c
vb
; c
vb
=
c
0
Φ+λΦ+c
e
vb
γ
γ +
Ψ+Φ
1+Φ
Φ
c
2
= c
0
−
c
0
− c
e
vb
Ψ
1+Φ
=
c
vb
Ψ+c
0
Φ
1+Φ
(3.62)
One easily recognizes that for Φ →∞(c
2
= c
0
, c
vb
= c
1
= c
0
+ λ)alldiffusion
effects are suppressed and that for Φ → 0(c
vb
= c
e
vb
, c
2
= c
1
= c
e
vb
· Ψ=c
e
v
)
equilibrium is approached. Since Ψ < 1, it is always c
vb
>c
1
(due to the
potential well). Mostly (except for an extremely high c
0
) one also has c
2
<c
vb
and c
1
>c
0
.Whetherc
2
<c
0
or c
2
>c
0
(dip or peak in front of the moving
boundary) depends upon the circumstances.
The difference c
1
− c
2
, which is proportional to the retarding force P
v
,
increases from 0 at Φ = 0 to λ at Φ = ∞. For large values of λ this in-
crease occurs monotonously; for small λ the function P
v
(Φ) runs through a
maximum. In Fig. 3.11 the function Φ(P) has schematically been derived by
graphical determination of the difference P −P
v
. One recognizes that for each
value of P either one or three values of Φ exist (Fig. 3.11). In the first case one
has a continuous transition from the state of a boundary loaded with vacan-
cies to the broken away state, in the latter case a discontinuous transition. In
this case the transition point (indicated by the dashed lines) cannot exactly
be defined. For very high and very low velocities, however, a single solution
v = v(P ) always exists,
Φ
H
=
P
Θ
−
hλ
Θ
−
h
P
{c
e
v
(1 − Ψ) + γ (c
e
vb
− c
0
) − λ (Ψ + γ)}→
P − hλ
Θ
Φ
L
=
P
h (c
e
vb
− c
0
)+Θ
∼
=
P
h (c
e
vb
− c
0
)
(3.63)
© 2010 by Taylor and Francis Group, LLC

3.3 Drag Effects During Grain Boundary Motion 163
3.3.5 Drag Effects by Second-Phase Particles
It is common knowledge that second phase particles drag grain boundary
motion [203]–[207]. The physical basis of this drag effect is the attraction force
between particle and grain boundary which is due to the reduction of grain
boundary or interface energy upon contact of particle and grain boundary.
The simplest and commonly exclusively attraction force considered is the well-
known “Zener force,” which appears when a particle intersects the boundary
and in doing so eliminates the area of the boundary. For a spherical particle
with radius r and a planar grain boundary with specific energy γ the reduction
of grain boundary energy per particle ΔG is (Fig. 3.12)
ΔG = γ
1 − πr
2
(3.64)
Correspondingly, the maximum attraction force f
∗
is
f
∗
1
=2πrγ (3.65)
A more precise calculation for a flexible boundary gives the Zener force as
[203]
f
∗
1
= πrγ (3.66a)
Actually if N is the number of particles per unit volume of the system, the
volume fraction of the particles is c =4/3πr
3
N. The particles in contact with
the boundary are confined to a volume 2r·1cm
2
, i.e. n, the number of particles
per 1 cm
2
of a grain boundary, is equal to n =2rN, n =3c/(2πr
2
). Thus the
maximum pinning force
f
max
= nf
∗
1
= πrγ · 3c/(2πr
2
)=
3
2
cγ/r (3.66b)
Eq.(3.66a) is the well-known Zener equation for the back driving force on mov-
ing grain boundaries in two phase alloys, which is utilized for the control of
grain size during recrystallization and grain growth. The Zener force, however,
is not the only attraction force in a particle-boundary system. For instance,
if a particle has a coherent interface with the matrix and correspondingly a
low free energy (surface tension), this advantage will be lost when the par-
ticle is swept by the boundary, since grain boundary migration changes the
orientation of the matrix in contact with the particle and, consequently, the
interface energy changes by [208]
ΔG =4πr
2
(γ
2
− γ
1
) (3.67)
and the maximum drag force is
f
∗
2
=8πr (γ
2
− γ
1
) (3.68)
© 2010 by Taylor and Francis Group, LLC
