Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

144 3 Grain Boundary Motion

planes that constitute the surfaces of the adjoining grains in a bicrystal have

a diﬀerent surface tension Δγ

, the boundary feels a driving force

P =2Δγ

/λ (3.12)

where λ is the thickness of the crystals. Decreasing the thickness, e.g. by fab-

rication of a thin sheet, not only increases the driving force, but, as will be

shown below, a drag from the free surface. It is felt that the optimal value of

P in this case is about 10

−4

MPa.

The list of potential driving forces for grain boundary migration is very

long and cannot be comprehensively covered here. Other major driving forces

are: a temperature gradient (∇T (P =ΔSδ∇T/(Ω

)), where ΔS is the en-

tropy diﬀerence between the bulk of a grain and the grain boundary, δ is the

grain boundary thickness, and Ω

the molar volume. Under optimal condi-

tions ∇T

∼

K/m, ΔS ≈ ΔS

≈ R, P

∼

−5

MPa; an anisotropy of the

elastic constants (P = τ

/[2 · [1/(E

) − 1/(E

)]]), where τ is the stress, E

are Young’s moduli of the diﬀerently oriented crystals. For a stress on the

order of 10 MPa one obtains a driving force P

∼

−5

− 10

−4

MPa.

The origin of these driving forces and their approximate magnitudes are

listed in Table 3.1.

3.3 Drag Eﬀects During Grain Boundary Motion

3.3.1 Origin of Drag Eﬀects

Whenever there is an interaction between a grain boundary and other imper-

fections in the crystal, this interaction will aﬀect grain boundary motion. Such

imperfections can be vacancies, dislocations, interface boundaries or external

crystal surfaces. Their interaction with the grain boundary is of very diﬀerent

nature and thus will be treated in separate sections below.

3.3.2 Impurity Drag in Ideal Solute Solutions

It is a common experience that grain boundary motion progresses much faster

in pure metals than in alloys, even dilute alloys. This must be due to the eﬀect

of solute atoms on grain boundary motion [193]–[196]. If there is an interaction

energy U (energy gain) between boundary and impurity atoms, these solute

atoms will tend to segregate to the boundary. In fact, if thermal equilibrium

could be established at all temperatures, and the boundary could adsorb an

unlimited number of impurities — like in the case of the Henry isotherm —

all solute atoms would end up in the boundary at T = 0 K. Owing to thermal

agitation (entropy eﬀect), for T>0 the concentration in the boundary will

3.3 Drag Eﬀects During Grain Boundary Motion 145

= c

exp





(3.13)

where c

is the volume impurity concentration

. When the grain boundary

moves, the segregated atoms will attempt to remain in the boundary, i.e. the

boundary has to drag its impurity load and can only migrate as fast as the

slowly moving impurities.

In the simplest approximation [193] one can assume that the segregated

impurities have to move along with the boundary and, therefore, exert a drag

force P

= n · f = n

· f = n

f · c

· e

U/kT

(3.14)

where n is the number of foreign atoms per unit area of the boundary, f is

the attraction force between boundary and a foreign atom (see, for instance,

[193]), n

is the number of lattice sites per unit area of the boundary.

If boundary and foreign atoms move together the net velocity of the segre-

gated solutes read

v = B · f =

f (3.15)

where D = D

exp



−Q



is the bulk diﬀusion coeﬃcient of the solute atoms.

The boundary moves according to Eq (3.6) with the velocity

v = m

· (P − P

)=m

(P − nf )=m



P −

n · vkT



(3.16)

and, therefore

v =

n·m

≈

exp



−

+ U



(3.17)

When the driving force increases it will ﬁnally reach a critical value where the

segregated impurities will no longer be able to keep up with the boundary.

Then the boundary will detach from the impurity cloud and move as a free

boundary with the speed

v = m

· P (3.18)

In this very simple model all atoms will detach from the boundary at the

same time. For a more realistic approach one has to consider the diﬀusion

of the solute atoms with the moving boundaries as proposed by Cahn and

L¨ucke [194, 195].

Due to the motion of the grain boundary the concentration distribution of

solute atoms will be altered. We are interested in the steady-state concentra-

tion (c(x, y, z)) of solute atoms in the presence of a boundary moving with

This is only true if there is no interaction between the solutes in the boundary. If this

constraint is relaxed a diﬀerent isotherm has to be used, as will be addressed in Sec. 3.3.3.

146 3 Grain Boundary Motion

constant velocity v. If we assume a planar boundary moving in x-direction,

the problem can be reduced to a one-dimensional diﬀusion equation

∂c

∂t

= D

∂

∂x

∂

∂x





(3.19)

with D the volume diﬀusion coeﬃcient and c = c

for x →±∞. This diﬀusion

equation is time dependent, since the grain boundary changes position with

time, as does the concentration distribution attached to it. In a coordinate

system aﬃxed to a grain boundary moving with constant speed the concen-

tration distribution remains stationary, i.e. ∂c/∂t = 0. For sake of simplicity,

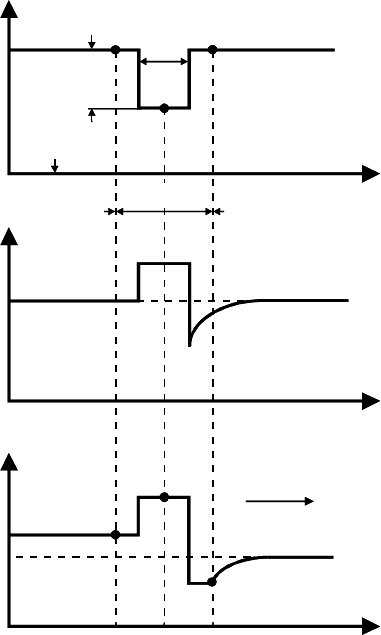
we shall assume (Fig. 3.5a) that

U(x)=



0 |x|≥a

−H

|x|≤a

(3.20)

Thus, dU/dx = 0 except for x = ± a. Using the Galilei transformation

x = x



− vt (3.21)

we obtain the diﬀusion equation in the coordinate system moving along with

the grain boundary at its origin

∂c

∂t

= D

∂

∂x

+ v

∂c

∂x

= 0 (3.22)

(x = ±a; c = c

,x= ±∞) which yields the solution

c(x)=c

+ c

−

(3.23)

with c

, c

being integration constants. For range I (behind the boundary)

(x)=c

(3.24a)

because of c(x)=c

for x = −∞.

For range II (in front of the boundary)

(x)=c

+(c

− c

) e

−

(3.24b)

with c

= c(+a).

Owing to the discontinuity of the potential U for x = ± a the constant c

and the concentration distribution inside the boundary cannot be calculated

in closed form

. However, during steady-state migration the diﬀusive ﬂux

A closed form solution is possible, when another shape of the potential U(x)isused,e.g.a

triangular potential, where |dU/dx| < ∞. This renders the solution of the diﬀusion equation

more diﬃcult for the range dU/dx = 0, but the analysis yields a result very similar to the

solution given here.

3.3 Drag Eﬀects During Grain Boundary Motion 147

must be constant everywhere, i.e. equal to the convective ﬂux j

= vc

.For

a boundary comprising a single atomic layer B (Fig. 3.5c) we obtain for the

ﬂux through the interface: range II/ boundary (B) (x = a)

−

− c

− vc

= −vc

(3.25a)

and the interface: boundary (B) / range I (x = − a)

− c

−

− vc

= −vc

(3.25b)

The ﬁrst two terms of Eq. (3.20a) represent the diﬀusion ﬂux through the

interface B/II in terms of the diﬀerence of the number of atomic jumps from

plane B to plane 2 and from plane 2 to plane B:

ν exp



−

+ H



− c

ν exp



−



(3.26)

where H

is the activation enthalpy of volume diﬀusion. The same holds for

Eq. (3.25b). Eqs. (3.24b, 3.25a,b) can be solved with regard to c

and c

We obtain, using Φ = bv/D and Ψ = e

−H

/kT

= c

(3.27a)

= c

1+Φ

Ψ+Φ

≥ c

(3.27b)



1 −

Φ(1− Ψ)

(1+Φ)(Ψ+Φ)



(3.27c)

The corresponding concentration distribution is given in Fig. 3.5c.

The concentration c

behind the boundary is here always equal to the initial

concentration c

.SinceΨ< 1, the boundary concentration c

.Further,

, i.e. there is a concentration dip in front of the boundary.

As discussed above, the elementary step of grain boundary motion is as-

sumed to consist of the jump of single atoms across the boundary from one

crystal to the other. We consider boundary motion from left to right in Fig.

3.5 which corresponds to a net atom jump to the left. By such a jump the

total free energy of the system may be altered for two reasons:

(i) If there is a driving force P (free energy per cm

) causing the boundary

to move to the right, the energy is decreased by the amount P Ω

≈ Pb

per jump, where Ω

is the atomic volume. Conversely, for backward

jumps the energy is increased by this amount.

(ii) If the boundary moves by one atomic step to the right, the impurities

located before in plane 2 are now situated in plane B and the ones of

plane B are now in plane 1. This corresponds to an energy change per

atom jump ΔH = c

− c

. A backward jump leads to an increase

ΔH = c

− c

148 3 Grain Boundary Motion

(b)

(c)

Plane

1B2

Range II

(a)

Range I

(b)

(c)

Plane

1B21B2

Range II

(a)

Range I

FIGURE 3.5

One-atomic boundary (a) energy level of an impurity in bulk and boundary;

(b) impurity concentration dependence across the boundary; (c) concentration

dependence in atomistic model; 1,2 denote atomic positions next to boundary

in the crystal, and B position in the boundary.

3.3 Drag Eﬀects During Grain Boundary Motion 149

Free

Loaded

Free

Loaded

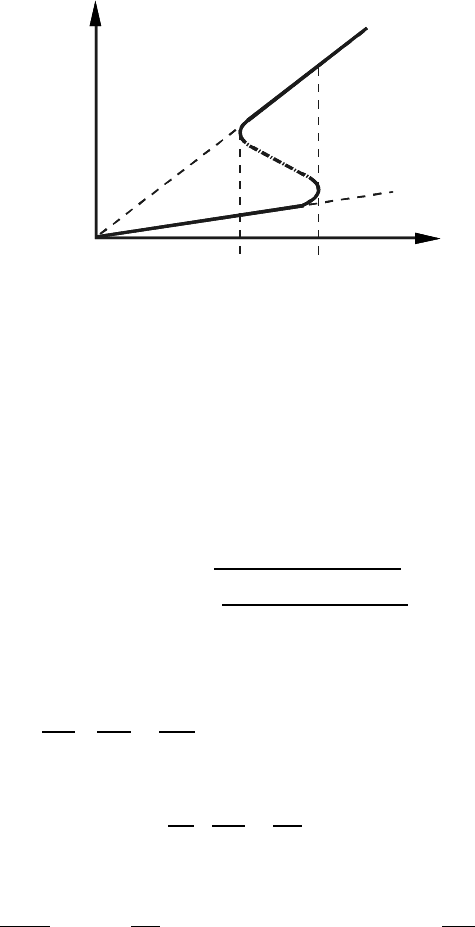
FIGURE 3.6

Dependence of grain boundary migration rate on driving force in the presence

of impurity drag. In the interval denoted by T the transition from the loaded

to the free boundary and vice versa occurs discontinuously.

If one supposes that the basic activation energy H

for such a jump is de-

creased in the case of a forward jump and increased in the case of a backward

jump by half of these energy changes, one obtains for the net velocity

v = bν

⎧

⎨

⎩

exp



−

−Pb

/2−H

−c

)/2



−exp



−

−Pb

/2+H

−c

)/2



⎫

⎬

⎭

(3.28)

Assuming that Pb

 kT and H

− c

)  kT the exponential function

can be expanded to give

v =



−

2kT

− c

)



= m (P − P

(v)) (3.29a)

P =

− c

) (3.29b)

with

m =

· (c

− c

) ,D

= νb

exp



−



(3.29c)

m is the mobility of the grain boundary without impurity atmosphere, and

is the retarding force due to the impurities. The important point is that c

and c

and thus also P

depend upon the velocity v of the boundary so that

the dependence v = v(P ) is contained only implicitly in Eq. (3.29a). Only the

150 3 Grain Boundary Motion

inverse function P = P (v) can explicitly be written (3.29b).

The introduction of the expressions for c

(Eq. (3.27a)) into Eq. (3.29b)

leads to an equation f(v, P) = 0 which is of third order in v.Thepositive

roots of this equation represent the function v = v(P ). In general, the solution

v(P ) cannot be given in closed form; only for very high (v

)andverylow(v

)

velocities are approximate expressions possible. In zero order approximation

one obtains

P ; (3.30a)

[exp (H

/kT ) − 1]

· P (3.30b)

The velocity v

describes the velocity of a free boundary, i.e. a boundary

broken away from the impurity atmosphere. The velocity v

is determined

by the diﬀusion of the impurities together with the moving boundary. At

intermediate values of v a transition from the boundary loaded with impurities

to the broken away boundary occurs. This transition range (T in Fig. 3.6) is

characterized by a very rapid increase in the velocity with increasing driving

force P . However, it is stressed that in this transition regime the boundary

also will move either as a loaded or as a free boundary or at some point

can change from one state to the other, as conﬁrmed experimentally (Fig.

3.7). This implies that the boundary cannot remain in the transition state

over an extended period of time as claimed previously to explain a nonlinear

relationship between grain boundary velocity and driving force.

3.3.3 Impurity Drag in Regular Solutions

Eq. (3.30) predicts that the mobility of the loaded grain boundary ought to

decrease with increasing impurity concentration m ∼ 1/c

and that the activa-

tion enthalpy H

of the mobility is diﬀerent for the free and loaded boundary,

but in both cases H

is independent of impurity concentration. This, how-

ever, is at variance with experimental results (Fig. 3.8). The concentration

dependence of the activation energy indicates that segregated atoms in the

boundary cannot be treated as a dilute solid solution, i.e. without interaction

of the segregated atoms. If there is solute-solute interaction in the bound-

ary, the impurity concentration in the boundary cannot be represented by

Eq. (3.13) (the Henry isotherm) anymore. Instead, the solutes in the bound-

aries have to be treated as a regular solution rather than an ideal solution

[197]. To simplify the mathematical treatment, we shall assume in the follow-

ing that the concentration proﬁle of solute is always given by the equilibrium

concentrations in the bulk c

and in the boundary c

When a boundary moves together with its segregated impurities, the ve-

locity of the impurity atoms v

should be equal to the boundary velocity

3.3 Drag Eﬀects During Grain Boundary Motion 151

position [µm]

time [s]

v = 1.8µm/s

v = 25.2µm/s

0 20 60 80 10040 200180160140120

400

800

1200

1600

position [µm]

time [s]

v = 1.8µm/s

v = 25.2µm/s

0 20 60 80 10040 200180160140120

400

800

1200

1600

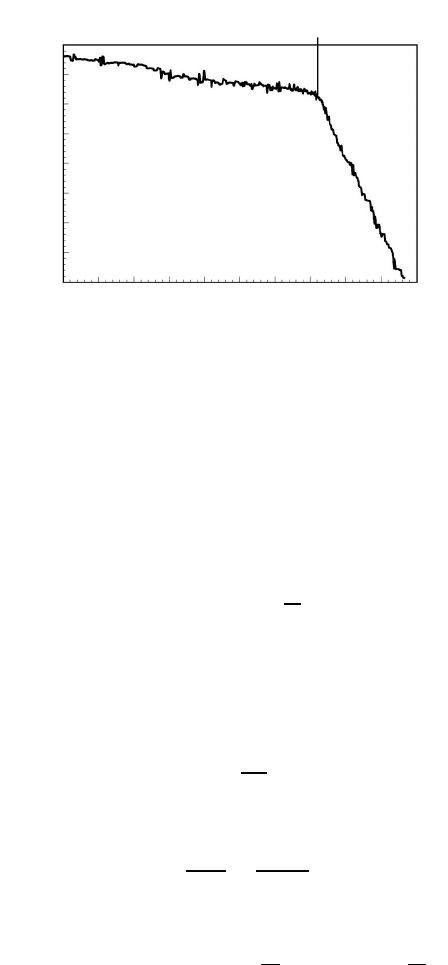
FIGURE 3.7

Recording of grain boundary position with annealing time in an Al bicrystal.

At t

the grain boundary unzips from its impurity cloud and moves freely.

Note discontinuous transition without intermediate stage.

. If the boundary moves under the action of an external driving force P ,it

imparts the same driving force to the impurities carried along

= m

P = v

(3.31)

where m

and m

are the mobilities of boundary and impurity atoms, re-

spectively. Γ = c

−c

is the diﬀerence between the concentration of adsorbed

impurities in the boundary c

and the bulk concentration c

.WiththeNernst-

Einstein relation

(3.32)

where D is the respective diﬀusion coeﬃcient, Eq. (3.31) yields

Γ · kT

(3.33)

For dilute (volume) solutions one may use the Henry isotherm

Γ=z · B · c

− c

= c



− 1



∼

(3.34)

for c

 c

.(B = e

/kT

= e

−S

— Gibbs free energy of adsorp-

tion, S

— adsorption entropy, H

— interaction enthalpy of impurity atoms

with the boundary, z — number of adsorption sites in the boundary.) Eqs.

152 3 Grain Boundary Motion

-4

-3

c [% at.]

0.5

1.0

1.5

2.0

2.5

3.0

[

]

-4

-3

[

]

100

150

200

250

c [at.%]

-4

-3

0.5

1.0

1.5

2.0

2.5

3.0

100

150

200

250

-04

-03

c [% at.]

[

]

0.0001 0.001

100

1000

10000

100000

1E+006

1E+007

1E+008

1E+009

1E+010

/s]

c [at.%]

-4

-3

(a)

(b)

[kJ/mol]

[eV]

-4

-3

c [% at.]

0.5

1.0

1.5

2.0

2.5

3.0

[

]

-4

-3

[

]

100

150

200

250

c [at.%]

-4

-3

0.5

1.0

1.5

2.0

2.5

3.0

100

150

200

250

-04

-03

c [% at.]

[

]

0.0001 0.001

100

1000

10000

100000

1E+006

1E+007

1E+008

1E+009

1E+010

/s]

c [at.%]

-4

-3

(a)

(b)

[kJ/mol]

[eV]

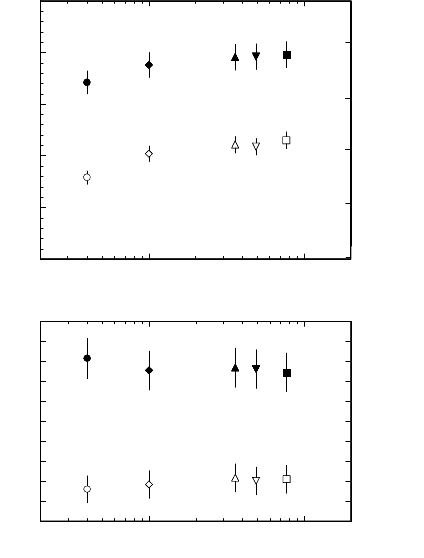
FIGURE 3.8

Dependence of activation enthalpy H and preexponential factor A

of the

reduced grain boundary mobility for 38.2

◦

(open symbols) and 40.5

◦

(ﬁlled

symbols) 111 tilt grain boundaries on impurity content in pure Al: ◦, • —

AlI; ♦,  —AlII;,  — AlIII; ,  —AlIV;,  —AlV.

3.3 Drag Eﬀects During Grain Boundary Motion 153

(3.31)–(3.34) render the known expression for the mobility of a boundary with

impurities:

−

(

)

kT · c

(3.35)

where D

is the diﬀusion pre-exponential factor, H

is the activation enthalpy

for (volume) diﬀusion of the impurity atoms. According to Eq.(3.35) the ac-

tivation enthalpy for grain boundary migration is the sum of two activation

enthalpies, impurity diﬀusion and impurity adsorption. The pre-exponential

mobility factor changes inversely proportionally to the impurity concentration

contrary to experimental results. As evident from Fig. 3.8, even at the low-

est impurity content, the activation enthalpy rises with increasing impurity

concentration, whereas the pre-exponential factor remains essentially at the

same level.

If there is a strong tendency toward segregation, the boundary impurity

concentration may be high although the volume impurity concentration is

small. For high impurity concentrations in the boundary it is necessary to

take into account the mutual interaction of adsorbed atoms in the bound-

ary. Also, grain boundaries are inhomogeneous, i.e. not every site in the grain

boundary is equally favorable for impurity segregation. The essential point

here is that this inhomogeneity plays an important role in the adsorption dur-

ing the process of migration and thus has to be taken into account.

In the following we shall consider the interaction of impurities with grain

boundaries in terms of adsorption. This allows us to express an inﬂuence of

adsorption on both the activation enthalpy and the pre-exponential mobility

factor. We consider a true binary system with bulk concentrations c

and c

and assume that the grain boundary chemistry is in equilibrium with the bulk,

in spite of grain boundary motion



,T,c



= μ

(p, T, c

) (3.36)



,T,c



= μ

(p, T, c

) (3.37)

where μ

, μ

,andμ

, μ

are the chemical potentials of the ﬁrst and second

component in the bulk and in the boundary, respectively, and c

1,2

denote the

respective boundary concentrations. The activities of atoms in both the bulk

) and the boundary





are related by





· e

(γ

−γ

)

(3.38)

where γ

and γ

are the grain boundary surface tensions of the pure ﬁrst and

second component, respectively, and

= −



∂μ

∂γ



p,T,γ

and ω

= −



∂μ

∂γ



p,T,γ

(3.39)